گام به گام تمرین صفحه 100 درس 6 ریاضی نهم (خط و معادله های خطی)

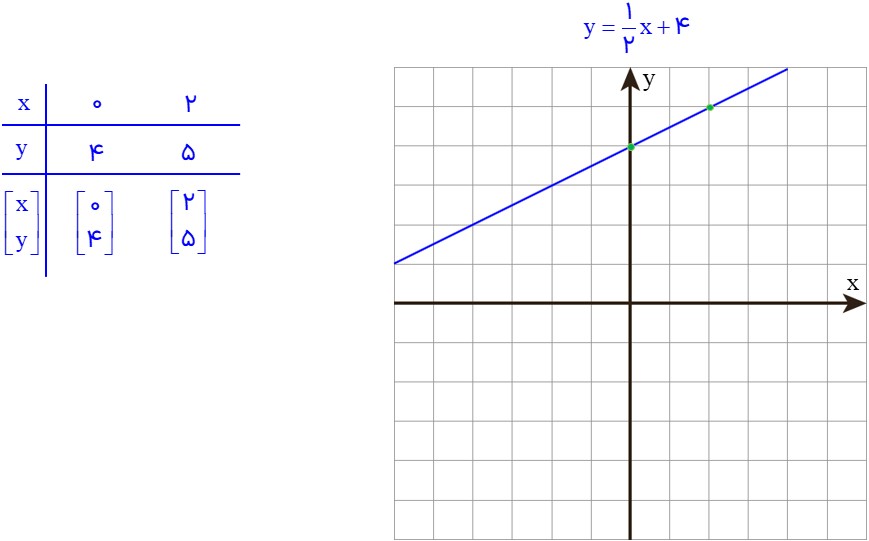
الف

خیر؛ زیرا:

\( - 1 \ne \frac{1}{2} \times 2 + 4 = 5\)

ب

\(\begin{array}{l}x = 0 \Rightarrow y = \frac{1}{2}x + 4 = \frac{1}{2} \times 0 + 4 = 4 \Rightarrow \left[ {\begin{array}{*{20}{c}}0\\4\end{array}} \right]\\\\y = 0 \Rightarrow 0 = \frac{1}{2}x + 4 \Rightarrow \frac{1}{2}x = - 4 \Rightarrow x = - 8 \Rightarrow \left[ {\begin{array}{*{20}{c}}{ - 8}\\0\end{array}} \right]\end{array}\)

ج

\(\begin{array}{l}y = \frac{1}{2} \times ( - 1) + 4\\\\y = - \frac{1}{2} + 4 = \frac{7}{2}\end{array}\)

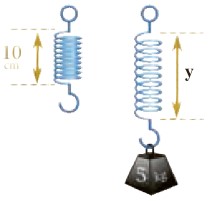
\(y = 0/8 \times 5 + 10 = 4 + 10 = 14\)

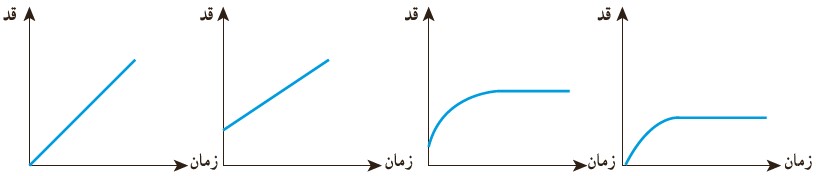
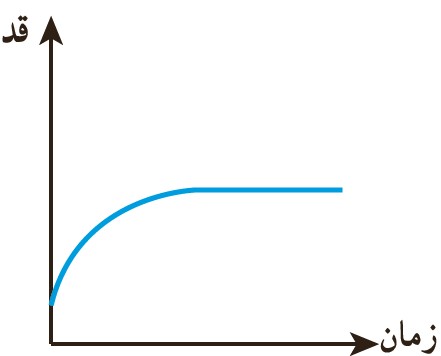
اگر هنگام تولد نوزاد را زمان صفر در نظر بگیریم، نوزاد دارای قد اولیه است که به مرور زمان قد او افزایش پیدا می کند و در سنین بزرگسالی، افزایش طول قد انسان به صفر می رسد و مقدار قد انسان ثابت می شود.

\(y = 3x\) (الف

\(y = 2x - 1\) (ب

\(y = 3x + 1\) (ج

\(\begin{array}{l}x = 0 \Rightarrow y = - x + 2 = - (0) + 2 = 2 \Rightarrow \left[ {\begin{array}{*{20}{c}}0\\2\end{array}} \right]\\\\y = 0 \Rightarrow 0 = - x + 2 \Rightarrow - x = - 2 \Rightarrow x = 2 \Rightarrow \left[ {\begin{array}{*{20}{c}}2\\0\end{array}} \right]\end{array}\)

\(y = - \frac{3}{5} \times 5 + 4 = - 3 + 4 = 1\)

الف

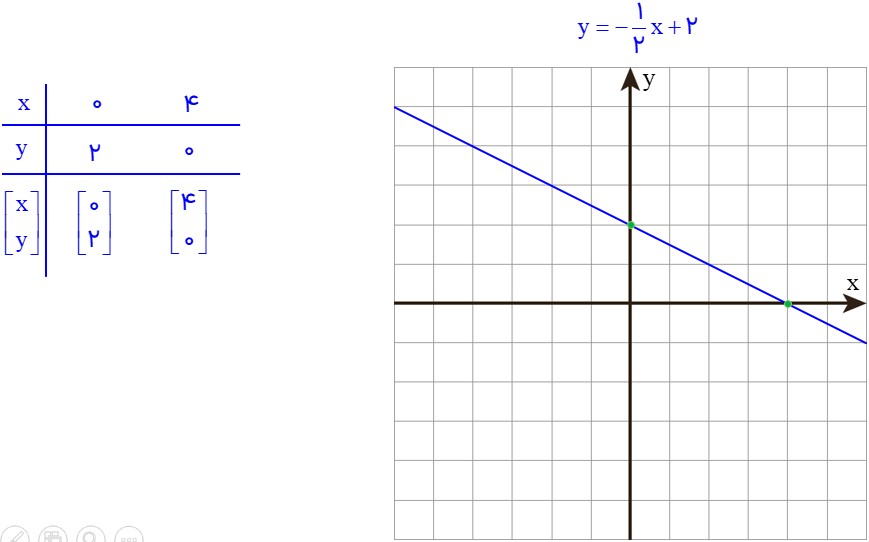
ب

بله:

\(3 = - \frac{1}{2} \times ( - 2) + 2 = 1 + 2\)

نقطه ای به طول -1 :

\(y = - \frac{1}{2}( - 1) + 2 = \frac{1}{2} + 2 = \frac{3}{2}\)

پ

نقطه ای به عرض -2 :

\(\begin{array}{l} - 2 = - \frac{1}{2}x + 2\\\\\frac{1}{2}x = 2 + 2 = 4\\\\x = \frac{4}{{\frac{1}{2}}} = 8\end{array}\)

ت

محل برخورد خط با محور مختصات برابر است با:

\(\begin{array}{l}x = 0 \Rightarrow y = - \frac{1}{2}x + 2 = - \frac{1}{2}(0) + 2 = 2 \Rightarrow \left[ {\begin{array}{*{20}{c}}0\\2\end{array}} \right]\\\\y = 0 \Rightarrow 0 = - \frac{1}{2}x + 2 \Rightarrow \frac{1}{2}x = 2 \Rightarrow x = \frac{2}{{\frac{1}{2}}} = 4 \Rightarrow \left[ {\begin{array}{*{20}{c}}4\\0\end{array}} \right]\end{array}\)