1736019749.png)
گام به گام فعّالیت صفحه 105 درس 6 ریاضی نهم (خط و معادله های خطی)
تعداد بازدید : 62.29Mپاسخ فعّالیت صفحه 105 ریاضی نهم
-گام به گام فعّالیت صفحه 105 درس خط و معادله های خطی
-فعّالیت صفحه 105 درس 6
-1 الف نقطه های \(\left[ \begin{array}{l}2\\0\end{array} \right]\) و \(\left[ \begin{array}{l}\;2\\ - 1\end{array} \right]\) را در دستگاه مختصات نشان دهید و خطی را رسم کنید که از این دو نقطه می گذرد.
ب روی خط، دو نقطه انتخاب کنید و مختصات آنها را بنویسید. \(\left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\;\;\left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\)
پ اگر نقطهٔ دیگری روی این خط در نظر بگیریم، طول آن برابر است با:
ت یک نقطهٔ دلخواه به طول 2 بنویسید و روی محور مختصات نشان دهید: \(\left[ \begin{array}{l}2\\{\kern 1pt} \end{array} \right]\)
تمام نقطه ها به طول 2 روی خط بالا قرار می گیرند و معادلهٔ آنها به صورت x=2 است.
الف
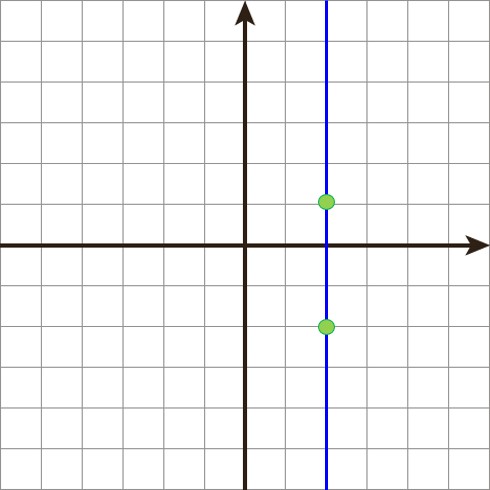
ب
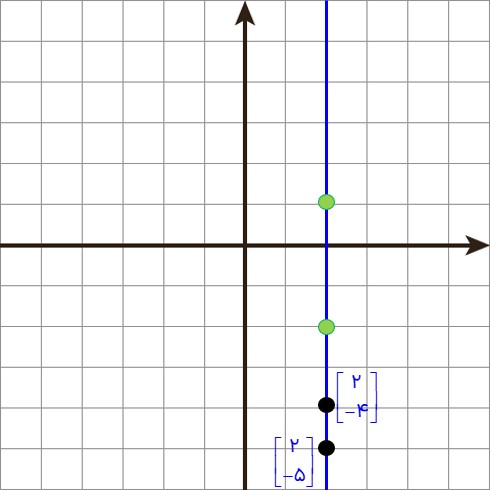
\(\left[ {\begin{array}{*{20}{c}}2\\{ - 4}\end{array}} \right]\,\left[ {\begin{array}{*{20}{c}}2\\{ - 5}\end{array}} \right]\)
پ
طول آن برابر با 2 می باشد.
ت
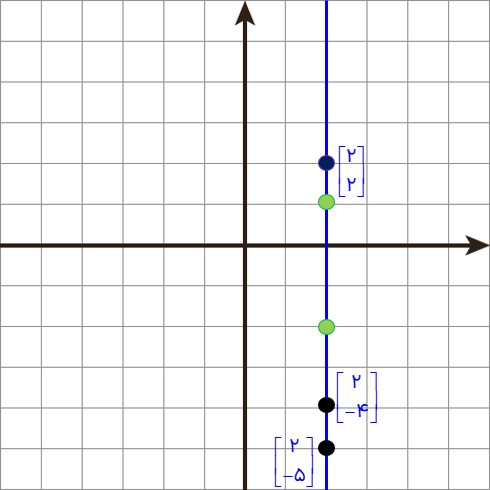
\(\left[ {\begin{array}{*{20}{c}}2\\2\end{array}} \right]\)
2 صورت کلی معادله های خطی به صورت ax+by=c است.
الف با توجه به مقدارهای نوشته شده، معادلهٔ خط را بنویسید؛ کدام خط از مبدأ می گذرد؟
\(\begin{array}{l}a = 2\,\,\,,\,\,\,b = 3\,\,\,,\,\,\,c = 4\,\,\, \to \\\\a = - 1\,\,\,,\,\,\,b = 2\,\,\,,\,\,\,c = 0\,\,\, \to \end{array}\)
ب با توجه به خط های داده شده، مقدارهای a، b و c را پیدا کنید.
\(\begin{array}{l} - 3x + 2y = 2\,\,\, \to \,\,\,a = \,\,\,\,\,\,\,\,\,\,b = \,\,\,\,\,\,\,\,\,\,c = \\\\y = 2x + 1\,\,\, \to \,\,\,\,\,\,\,\,\,\,\,a = \,\,\,\,\,\,\,\,\,\,b = \,\,\,\,\,\,\,\,\,\,c = \end{array}\)
ج برای خط x=2 مقدارهای a، b و c را بنویسید.
\(\begin{array}{l}ax + by = c\,\,\, \to \,\,\,x = 2\\ \downarrow \,\,\,\,\,\,\,\,\,\,\, \downarrow \,\,\,\,\,\,\,\,\,\,\, \downarrow \end{array}\)
الف
خط دوم؛ چون عرض از مبدأ آن صفر می باشد.
\(\begin{array}{l}a = 2\,\,\,,\,\,\,b = 3\,\,\,,\,\,\,c = 4 \Rightarrow 2x + 3y = 4\\\\x = 0 \Rightarrow 2(0) + 3y = 4 \Rightarrow y = \frac{4}{3}\\\\\left[ {\begin{array}{*{20}{c}}0\\{\frac{4}{3}}\end{array}} \right]\\\\a = - 1\,\,\,,\,\,\,b = 2\,\,\,,\,\,\,c = 0 \Rightarrow - x + 2y = 0\\\\x = 0 \Rightarrow y = 0\\\\\left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\end{array}\)
ب
\(\begin{array}{l} - 3x + 2y = 2\,\,\, \to \,\,\,a = - 3\,\,\,\,\,\,\,\,\,\,b = 2\,\,\,\,\,\,\,\,\,\,c = 2\\\\y = 2x + 1\,\,\, \to \,\,\,\,\,\,\,\,\,\,\,a = - 2\,\,\,\,\,\,\,\,\,\,\,b = 1\,\,\,\,\,\,\,\,\,\,\,c = 1\\\\y = 2x + 1 \Rightarrow - 2x + y = 1\end{array}\)
ج
\(\begin{array}{l}ax + by = c\,\,\, \to \,\,\,x = 2\\ \downarrow \,\,\,\,\,\,\,\,\,\,\, \downarrow \,\,\,\,\,\,\,\,\,\,\, \downarrow \\1\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,2\\\\a = 1\,\,\,\,\,,\,\,\,\,\,b = 0\,\,\,\,\,,\,\,\,\,\,c = 2\end{array}\)
3 الف مختصات نقطه های مشخص شده را روی خط بنویسید.
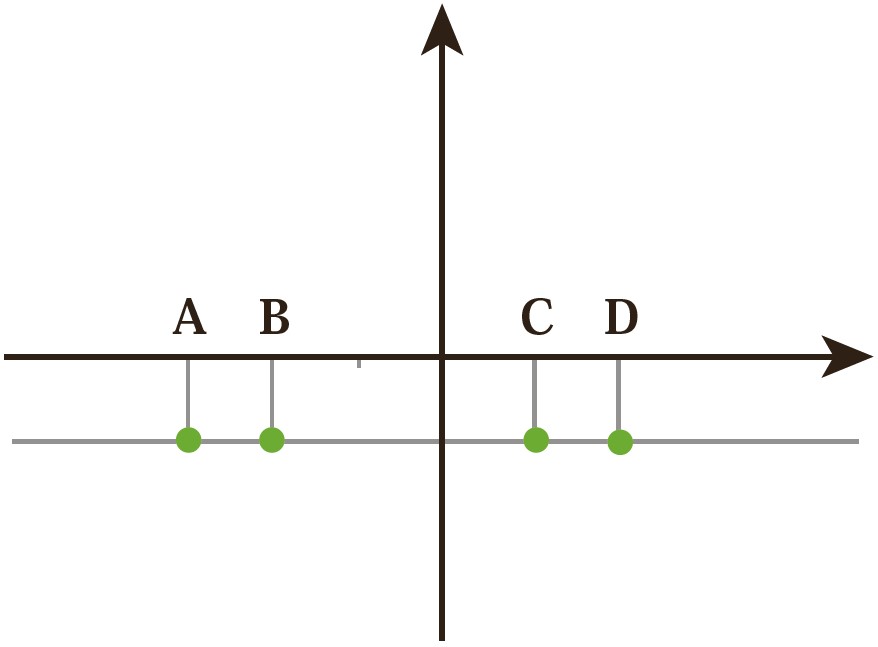
\(\begin{array}{l}A = \left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\;\;\;B = \left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\\\\C = \left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\;\;\;D = \left[ \begin{array}{l}\\{\kern 1pt} \end{array} \right]\end{array}\)
ب این نقطه ها چه ویژگی مشترکی دارند؟
پ معادلهٔ خط رسم شده را بنویسید.
ت در شکل کلی معادله های خطی به جای a، b و c چه عددهایی قرار دهیم تا معادلهٔ خطِ رسم شده به دست آید؟
ax+by=c
الف
\(\begin{array}{l}A = \left[ \begin{array}{l} - 3\\ - 1\end{array} \right]\;\;\;B = \left[ \begin{array}{l} - 2\\ - 1\end{array} \right]\\\\C = \left[ \begin{array}{l}1\\ - 1\end{array} \right]\;\;\;D = \left[ \begin{array}{l}2\\ - 1\end{array} \right]\end{array}\)
ب
دارای عرض یکسان می باشند.
پ
\(y = - 1\)
ت
\(a = 0\,\,\,\,\,,\,\,\,\,\,b = 1\,\,\,\,\,,\,\,\,\,\,c = - 1\)
4 مانند نمونه برای خط های داده شده شیب و عرض از مبدأ را پیدا کنید.
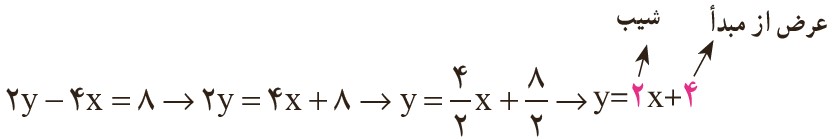
\(\begin{array}{l}3x - 2y = 6\\\\x + 3y - 9 = 0\end{array}\)
\(\begin{array}{l}3x - 2y = 6 \Rightarrow - 2y = - 3x + 6\\\\ \Rightarrow y = \frac{{ - 3}}{{ - 2}}x + \frac{6}{{ - 2}} \Rightarrow y = \frac{3}{2}x - 3\end{array}\)
\( = \frac{3}{2}\) شیب خط
\( = - 3\) عرض از مبدأ
\(\begin{array}{l}x + 3y - 9 = 0 \Rightarrow 3y = - x + 9\\\\ \Rightarrow y = - \frac{1}{3}x + \frac{9}{3} \Rightarrow y = - \frac{1}{3}x + 3\end{array}\)
\( = \frac{1}{3}\) شیب خط
\( = 3\) عرض از مبدأ
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
