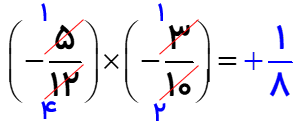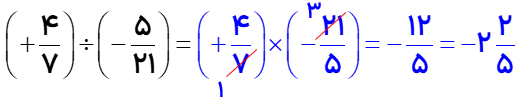درسنامه کامل ریاضی نهم فصل 2 عددهای حقیقی
تعداد بازدید : 7.27Mخلاصه نکات ریاضی نهم فصل 2 عددهای حقیقی - درسنامه شب امتحان ریاضی نهم فصل 2 عددهای حقیقی - جزوه شب امتحان ریاضی نهم نوبت اول فصل 2 عددهای حقیقی
ضرب و تقسیم و جمع و تفریق اعداد گویا
اعداد گویا
هر عددی که به کسر تبدیل شود عدد گویا نام دارد.( صورت و مخرج عدد صحیح و مخرج مخالف صفر باشد)
اعداد گویا را با حرف انگلیسیQ نمایش می دهند:
\(Q = \{ \left. {\frac{a}{b}} \right|{\rm{ }}a,b \in z,b \ne 0\} \)
جمع و تفریق اعداد کسری
مخرج مشترک گرفته که بهترین مخرج مشترک همان )ب . م. م) مخرج ها است.
مانند :
\(\left( { - \frac{5}{{12}}} \right) - \left( { - \frac{7}{{18}}} \right) = \frac{{ - 15 + 14}}{{36}} = - \frac{1}{{36}}\)(ب. م . م) مخرج ها \( \Rightarrow \left( {12,18} \right) = 36\)
ضرب اعداد کسری
فقط در ضرب میتوان قبل از جواب دادن صورت را با مخرج ساده کرد. سپس صورت ها در هم و مخرج ها در هم ضرب می شود.
مانند :
تقسیم اعداد کسری
تقسیم به ضرب تبدیل میشود کسر اولی در معکوس کسر دومی ضرب می شود.
(کسر اولی در معکوس کسر دومی ضرب می شود)
مانند :
مثال
حاصل عبارت زیر را به دست آورید.
\(\left( { + \frac{2}{3}} \right) \div \left[ {\left( { - \frac{1}{5}} \right) + \left( { + \frac{3}{5}} \right)} \right]\)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
مقایسه کسرها
مقایسه کسرها
از دو روش می توان استفاده کرد :
الف) هم مخرج کردن کسرها : ابتدا مخرج تمام کسرها را برابر کرده سپس کسرها را مقایسه می کنیم.
مثال
کسرهای زیر را از کوچک به بزرگ مرتب کنید.
\(\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}}\)
\(\begin{array}{l}\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}} \Rightarrow \frac{8}{{20}},\frac{{15}}{{20}},\frac{{10}}{{20}},\frac{{14}}{{20}} \Rightarrow \frac{2}{5} < \frac{1}{2} < \frac{7}{{10}} < \frac{3}{4}\\\\\left( {2,45,10} \right) = 20\end{array}\)
ب) تبدیل به عدد اعشار : صورت بر مخرج تقسیم و خارج قسمت تا دو رقم اعشار ادامه می دهیم.
مثال
کسرهای زیر را از کوچک به بزرگ مرتب کنید.
\(\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}}\)
\(\begin{array}{l}\frac{2}{5} = 0/40{\rm{ }},{\rm{ }}\frac{3}{4} = 0/75{\rm{ , }}\frac{1}{2} = 0/50{\rm{ , }}\frac{7}{{10}} = 0/70\\\\\frac{2}{5},\frac{1}{2},\frac{7}{{10}},\frac{3}{4}\end{array}\)
بین هر دو عدد گویا بی نهایت عدد گویا وجود دارد.
پیدا کردن کسرهایی بین دو عدد کسری
چند روش وجود دارد که دو روش کاربردی آن به صورت زیر است :
۱) صورت ها با هم و مخرج ها با هم جمع می کنیم
۲) ابتدا مخرج مشترک گرفته سپس صورت و مخرج را در یک واحد بیشتر از تعداد خواسته شده ضرب کنیم.
مثال
بین \(\frac{4}{5},\frac{3}{4}\) دو عدد گویا بنویسید؟
روش اول:
\(\frac{3}{4} < \frac{7}{9} < \frac{{11}}{{14}} < \frac{4}{5}\)
روش دوم:
\(\frac{3}{4},\frac{4}{5} \Rightarrow \frac{{15}}{{20}},\frac{{16}}{{20}} \Rightarrow \frac{{45}}{{60}},\frac{{48}}{{60}} \Rightarrow \frac{{45}}{{60}} < \frac{{46}}{{60}} < \frac{{47}}{{60}} < \frac{{48}}{{60}}\)
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
تبدیل کسر به اعداد اعشاری
عددهای اعشاری متناهی یا مختوم
اگر باقیمانده صورت بر مخرج کسر صفر شود آن کسر را مختوم نام دارد.مانند :
\(\frac{3}{4} = 0/75{\rm{ }},{\rm{ }}\frac{6}{5} = 1/25\)
اگر در تجزیه مخرج کسر عامل ۲ و ۵ باشند آن کسر مختوم است. مانند :
\(\begin{array}{l}\frac{3}{{20}} \Rightarrow 20 = {2^2} \times 5\\\\\frac{5}{8} \Rightarrow 8 = {2^3}\end{array}\)
عددهای اعشاری متناوب ساده
اگر در تقسیم صورت بر مخرج کسر در خارج قسمت عددی مرتب تکرار شود آن را متناوب ساده می گویند. مانند : (خط تیره روی عدد به معنی تکرار یا گردش عدد است.)
\(\begin{array}{l}\frac{5}{{11}} = 0/4545000 = 0/\overline {45} \\\\\frac{1}{3} = 0/33000 = 0/\overline 3 \end{array}\)
اگر در تجزیه مخرج کسر عامل ۲ و ۵ نباشند آن کسر متناوب ساده است، مانند :
\(\frac{3}{{77}} \Rightarrow 77 = 7 \times 11{\rm{ , }}\frac{6}{{13}}\)
عددهای اعشاری متناوب مرکب
اگر در تقسیم صورت بر مخرج کسر در خارج قسمت بعد از یک یا چند رقم اعشار به رقم های تکراری برسند به آن کسر متناوب مرکب می گویند؛ مانند :
\(\begin{array}{l}\frac{5}{6} = 0/833000 = 0/8\overline 3 {\rm{ }}\\,\\\frac{7}{{22}} = 0/31818000 = 0/3\overline {18} \end{array}\)
اگر در تجزیه مخرج کسر غیر از عامل ۲ و ۵ عامل دیگری باشند آن کسر متناوب مرکب است.
مانند:
\(\begin{array}{l}\frac{5}{{14}} \Rightarrow 14 = 2 \times 7\\,\\\frac{2}{{75}} \Rightarrow 75 = 3 \times {5^2}\end{array}\)
تهیه کننده:مسعود زیرکاری
اعداد گنگ
اعداد گنگ یا اصم
اعداد که تعداد ارقام اعشاری آنها نامتناهی و دارای دوره تناوب نباشند اعداد گنگ نام دارند.
1 مجموعه اعداد گنگ را با حرف انگلیسی Q یا \({Q^C}\) نشان می دهند.
2 اگر n مربع کامل نباشد آنگاه \(\sqrt n \) عددی گنگ است )یعنی اعدادی که جذر دقیق ندارند عدد گنگ هستند)
3 عدد \(\pi \)چون دارای دوره تناوب نیست عدد گنگ است )عدد\(\pi \)تا ۱۰ رقم اعشار :\(\pi = 3/1415926535\) )
4 بین دو عدد بی نهایت عدد گنگ وجود دارد.
مثال
بین هر دو عدد داده شده دو عدد گنگ بنویسید.
الف \(\sqrt 3 ,\sqrt 4 \)
\(\sqrt 3 < \sqrt {3/1} < \sqrt {3/2} < \sqrt 4 \)
ب\(3,2\)
\(2 = \sqrt 4 < \sqrt 5 < \sqrt 6 < \sqrt 9 = 3\)
مثال
عدد \(3 - \sqrt {10} \) بین کدام دو عدد صحیح متوالی قرار دارد؟
\(3 - \sqrt {16} < 3 - \sqrt {10} < 3 - \sqrt 9 \Rightarrow - 1 < 3 - 10 < 0\)
بین 0 و1 قرار دارد.
اعداد\(1 - \sqrt 5 ,\sqrt {17} \) را روی محور اعداد نمایش دهید.:
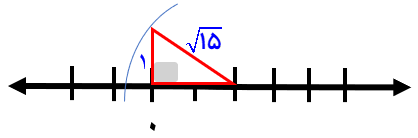
الف\(1 - \sqrt 5 \)
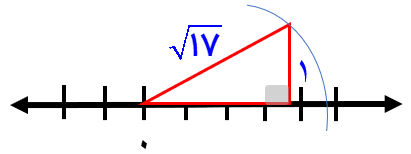
ب\(\sqrt {17} \)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
اعداد حقیقی
اعداد حقیقی
اجتماع مجموعه اعداد گویا و اعداد گنگ مجموعه اعداد حقیقی را تشکیل می دهد
\(Q \cup Q' = R\)
1 مجموعه اعداد حقیقی را با حرف انگلیسی R نشان می دهند.
2 نمودار ون مجموعه اعداد طبیعی (N) و اعداد حسابی (W) و اعداد صحیح (Z) و اعداد گویا (Q) و اعداد گنگ (Q’) و اعداد حقیقی (R) به صورت زیر است :
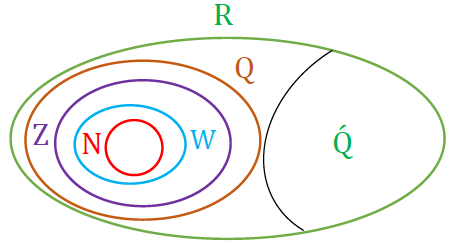
\(N \subseteq W \subseteq Z \subseteq Q \subseteq R{\rm{ }},{\rm{ }}Q' \subseteq R\)
نمایش اعداد حقیقی روی محور
چون اعداد حقیقی شامل اعداد گویا و گنگ هستند پس نمایش این اعداد به صورت یک خط ممتدی است. ( اگر علامت نامساوی سرکش داشته باشد دایره توپر و بدون سرکش دایره تو خالی قرار می دهیم)
مثال
مجموعه اعداد زیر را روی محور نشان دهید.
الف \(A = \{ x \in \left. R \right| - 2 \le x < 3\} \)
ب \(B = \{ x \in \left. R \right|1 \le x\} \)
مثال
مجموعه متناظر محور مقابل را بنویسید.
\(C = \{ x \in \left. R \right| - 3 < x < 3\} \)
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
قدر مطلق
قدر مطلق
فاصله ی نقطه نمایش یک عدد مانند a را از مبدا مختصات قدر مطلق a می نامیم و آن را به صورت |a| نشان می دهیم.
خواص قدر مطلق
الف) قدر مطلق عدد مثبت برابر است با خود آن عدد :\(x\rangle 0 \Rightarrow \left| x \right| = x\)
ب( قدر مطلق صفر برابر با صفر است :\(x = 0 \Rightarrow \left| x \right| = 0\)
ج) قدر مطلق عدد منفی برابر با قرینه آن عدد است :\(x < 0 \Rightarrow \left| x \right| = - x\)
مثال
عبارت های زیر را بدون استفاده از نماد قدر مطلق بنویسید.
1 \(\left| {4 - 6 \times {2^2} \div 3 + 2} \right|\)
\(\left| {4 - 6 \times {2^2} \div 3 + 2} \right| = \left| { - 2} \right| = 2\)
2 \(\left| {3 - \sqrt 2 } \right|\)
\(\left| {3 - \sqrt 2 } \right| = 3 - \sqrt 2 \)
3 \(\left| {{a^{20}} - {a^{30}}} \right|\)
\(\left| {{a^{20}} - {a^{30}}} \right| = {a^{30}} - {a^{20}}\)
مثال
اگر \(x = \frac{2}{3}\,\,,\,\,z = - \frac{1}{2}\,\,,\,\,y = 3\)باشد. حاصل عبارت زیر را به دست آورید.
\(\left| { - 6x - 4z} \right| + 2\left| y \right|\)
\(\left| { - 6x - 4z} \right| + 2\left| y \right| = \left| { - 6\left( {\frac{2}{3}} \right) - 4\left( { - \frac{1}{2}} \right)} \right| + 2\left| 3 \right| = \left| { - 4 + 2} \right| + 2\left( 3 \right) = 2 + 6 = 8\)
با توجه به مفهوم قدر مطلق همواره رابطه مقابل برقرار است :\(\sqrt {{a^2}} = \left| a \right|\)
حاصل هر عبارت را به دست آورید.
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} = \left| {2 - \sqrt 5 } \right| = - \left( {2 - \sqrt 5 } \right) = \sqrt 5 - 2\)
\(\sqrt {{{\left( {3\sqrt 2 - 2\sqrt 2 } \right)}^2}} \)
\(\sqrt {{{\left( {3\sqrt 2 - 2\sqrt 2 } \right)}^2}} = \left| {3\sqrt 2 - 2\sqrt 2 } \right| = 3\sqrt 2 - 2\sqrt 2 \)
تهیه کننده:مسعود زیرکاری



1736019749.png)