درسنامه کامل ریاضی نهم فصل 5 عبارت های جبری
تعداد بازدید : 7.28Mخلاصه نکات ریاضی نهم فصل 5 عبارت های جبری - درسنامه شب امتحان ریاضی نهم فصل 5 عبارت های جبری - جزوه شب امتحان ریاضی نهم نوبت اول فصل 5 عبارت های جبری
عبارت های جبری
عبارت جبری
عبارتی است که از اعداد و متغیر حروف (انگلیسی) تشکیل شده است.
یک جمله ای
عبارت جبری که از دو قسمت تشکیل شده است متغیر و عدد و بین آنها علامتی نباشد. (ضرب است)
مانند :
\( - 4xy,\frac{a}{3}\)
1فرم کلی یک جمله ای به صورت ax است که a عدد حقیقی و x متغیر و 12 عدد حسابی است.
2 هر عدد حقیقی به تنهایی یک جمله ای است چون متغیر آن صفر است.
3 اگر در عبارتی حروف زیر رادیکال یا حروف در مخرج یا حروف توان منفی داشته باشند آن عبارت یک جمله ای نیست.
مثال
کدام عبارت یک جمله ای است؟
\(\sqrt 3 x{y^2},4a + 2,7\sqrt x ,a{b^{ - 2}},\frac{3}{2}\)
\(4a + 2\)
درجه یک جمله ای
توان متغیر را درجه آن یک جمله ای می گویند.
مثال
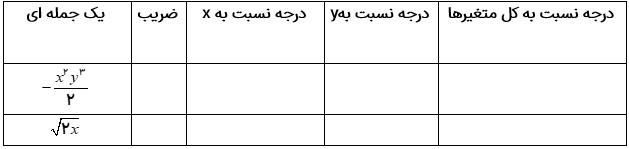
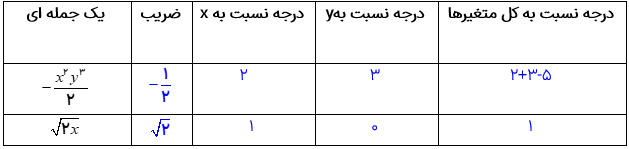
جدول زیر را کامل کنید.
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
یک جمله ای متشابه
یک جمله ای متشابه
یک جمله ای که متغیر و توان هر متغیر کاملا مثل هم باشند. مانند\(\left( {4xy, - 3yx} \right)\) که متشابه اند،ولی\(\left( { - 5{a^2}b,3a{b^2}} \right)\) نامتشابه هستند.
جمع و تفریق یک جمله ای های متشابه
ضرایب یک جمله ای را با هم جمع و تفریق می کنیم و متغیرها را کنار آن ها می نویسیم.
مثال
عبارت جبری مقابل را ساده کنید.
\( - 5ab + b - 6 + 3ab + 2b - 8b\)
\( - 5ab + b - 6 + 3ab + 2b - 8b = - 2ab - 5b - 6\)
ضرب و تقسیم یک جمله ای
در ضرب ضرایب در هم و متغیرها در هم ضرب میشود و در تقسیم ضرایب بر هم و متغیرها بر هم تقسیم می شوند.
مثال
عبارت های جبری زیر را ساده کنید.
\(3a( - 4ab - c)\)
\(3a( - 4ab - c) = - 12{a^{2b}} - 3ac\)
\(\frac{{24{x^2}{y^3}z}}{{3xyz}}\)
\(\frac{{24{x^2}{y^3}z}}{{3xyz}} = 8x{y^2}\)
عبارت جبری زیر را ساده کنید.
\( - 6{x^{2 + 5x}}(x - 2y) + 8xy\)
\( - 6{x^{2 + 5x}}(x - 2y) + 8xy = - 6{x^2} + 5{x^2} - 10xy + 8xy = {x^2} - 2xy\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
درجه چند جمله ای
درجه چند جمله ای
برای تعیین درجه چند جمله ای ، بزرگترین درجه نسبت به آن متغیر را در نظر می گیریم.
مثال
درجه نسبت به متغیر x در چند جمله ای \(\sqrt 5 {x^2}{y^3}z - 3xy + 2{x^2}{y^2} - x\) چند است؟
درجه x برابر ۳ است.
مثال
چند جمله ای زیر را نسبت به توان های نزولی a (از بزرگ به کوچک) مرتب کنید.
\({a^3}b{\rm{ }} - 3 + 2{a^3}{b^2} - 5ab{\rm{ }}\)
\({a^3}b{\rm{ }} - 3 + 2{a^3}{b^2} - 5ab{\rm{ }} = 2{a^3}{b^2} + {a^2}b - 5ab - 3\)
تهیه کننده: مسعود زیرکاری
اتحاد جبری
اتحاد جبری
اگر دو عبارت جبری به گونه ای باشند که با ازای تمام مقادیر دلخواه برای متغیرها مقدار یکسانی داشته باشد به تساوی جبری آنها اتحاد می گویند.
مثال
آیا \({(x - 2)^2} = {x^2} - 4x + 4\) یک اتحاد است؟ چرا؟
به ازای مقادیر دلخواه امتحان میکنیم اگر دو طرف تساوی یکی شد این تساوی یک اتحاد است.
\(\left\{ \begin{array}{l}x = - 4 \Rightarrow {( - 4 - 2)^2} = {( - 4)^2} - 4( - 4) + 4 \Rightarrow 36 = 36\\\\x = 5 \Rightarrow {(5 - 2)^2} = {5^2} - 4(5) + 4 \Rightarrow 9 = 9\end{array} \right.\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
اتحاد مربع دو جمله ای
اتحاد مربع دو جمله ای
الف) جبری:
\(\left\{ \begin{array}{l}{(a + b)^2} = {a^2} + 2ab + {b^2}\\{(a + b)^2} = {a^2} - 2ab + {b^2}\end{array} \right.\)
ب( کلامی :
(جمله دوم به توان2) +( 2 برابر جمله اول در دوم) + )جمله اول به توان 2) = (جمله دوم + جمله اول)
مثال
حاصل عبارت های جبری زیر را به کمک اتحاد به دست آورید.
\({(a - 2b)^2}\)
\({(a - 2b)^2} = {a^2} - 2(a)(2b) + {(2b)^2} = {a^2} - 4ab + 4{b^2}\)
\({(xy + 3)^2}\)
\({(xy + 3)^2} = {x^2}{y^2} + 2(xy)(3) + {3^2} = {x^2}{y^2} + 6xy + 9\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
اتحاد مزدوج
اتحاد مزدوج
الف) جبری :
\((a + b)(a - b) = {a^2} - {b^2}\)
ب( کلامی :
(جمله دوم به توان 2) - (جمله اول به توان 2) = (جمله دوم - جمله اول) × (جمله دوم + جمله اول)
مثال
حاصل عبارت های جبری زیر را به کمک اتحاد به دست آورید.
\((a - 3b)(a + 3b)\)
\((a - 3b)(a + 3b) = {a^2} - {(3b)^2} = {a^2} - 9{b^2}\)
\(\left( {2x + \frac{y}{2}} \right)\left( {2x - \frac{y}{2}} \right)\)
\(\left( {2x + \frac{y}{2}} \right)\left( {2x - \frac{y}{2}} \right) = {(2x)^2} - {(\frac{y}{2})^2} = 4{x^2} - \frac{{{y^2}}}{4}\)
حاصل عبارت جبری زیر را به کمک اتحاد به دست آورید.
\(\left( {2a - 3} \right)(2a + 4)\)
\(\left( {2a - 3} \right)(2a + 4) = {(2a)^2} + ( - 3 + 4)(2a) + ( - 3 \times 4) = 4{a^2} + 2a - 12\)
تهیه کننده: مسعود زیرکاری
تجزیه عبارت جبری
تجزیه عبارت جبری
نوشتن یک عبارت جبری به صورت حاصل ضرب چند عبارت دیگر را تجزیه می گویند.
روشهای تجزیه :
الف) فاکتور گیری
ب) با استفاده از اتحادها
فاکتور گیری
برای فاکتور گیری مراحل زیر را انجام می دهیم :
۱) (ب.م.م) ضرایب را تعیین میکنیم
۲) حروف مشترک با توان کمتر را انتخاب می کنیم
۳) (ب.م.م) و حروف مشترک را به عنوان فاکتور می گیریم
۴) تمام جملات را بر عامل فاکتور تقسیم کرده و جواب را داخل پرانتز می نویسیم
مثال
عبارت های جبری زیر را تجزیه کنید.
\(18xy - 12y\)
\(18xy - 12y = 6y(3x - 2)\)
\(16{a^{2b}} + 4a{b^2} - {y^4}\)
\(16{a^{2b}} + 4a{b^2} - {y^4} = {(2x + {y^2})^2}\)
تجزیه به کمک اتحاد مربع
۱) تعداد جملات ۳ جمله باشد
۲) جمله اول و جمله سوم جذر دقیق داشته باشند
مثال
عبارت های جبری زیر را تجزیه کنید.
\({a^2} - 6a + 9\)
\({a^2} - 6a + 9 = {(a - 3)^2}\)
\(4{x^2} + 4x{y^2} + {y^4}\)
\(4{x^2} + 4x{y^2} + {y^4} = {(2x + {y^2})^2}\)
تجزیه به کمک اتحاد جمله مشترک
۱) تعداد جملات ۳ جمله باشد
۲) جمله اول و جمله سوم جذر دقیق نداشته باشند
۳) ضریب x حاصل جمع و عدد آخر حاصل ضرب دو عدد را نشان می دهد
مثال
عبارت های جبری زیر را ساده کنید.
\({x^2} - 5x + 6\)
\({x^2} - 5x + 6 = (x - 3)(x - 2)\)
\({x^2} - 1x - 12\)
\({x^2} - 1x - 12 = (x - 4)(x + 3)\)
تجزیه به کمک اتحاد مزدوج
۱) تعداد جملات ۲ جمله باشد
۲) جملات اول و دوم جذر دقیق داشته باشند
۳) بین جملات علامت منفی باشد
مثال
عبارت های جبری زیر را ساده کنید.
\({a^2} - 9\)
\({a^2} - 9 = (a - 3)(a + 3)\)
\({x^4} - 16\)
\({x^4} - 16 = ({x^2} - 4)({x^2} + 4)\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
نامعادله
نامعادله
جواب های نامعادله مقادیری از متغیر هستند که به ازای آنها نامساوی برقرار است. همه ی جواب های نامعادله مجموعه جواب آن گفته می شود.
1 اگر به طرفین یک نا مساوی عدد اضافه یا عددی کم شود جهت نابرابری عوض نمی شود :
\(a < b \Rightarrow a + c < b + c\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,a < b \Rightarrow a - c < b - c\)
2 اگر طرفین یک نا مساوی در عدد مثبت ضرب یا بر عدد مثبت تقسیم کنیم جهت نابرابری عوض نمی شود:
\(a\rangle b \Rightarrow ac\rangle bc\,\,\,\,\,\,,\,\,\,\,\,\,a\rangle b \Rightarrow \frac{a}{c}\rangle \frac{b}{c}\)
3 اگر طرفین یک نا مساوی در عدد منفی ضرب یا بر عدد منفی تقسیم کنیم جهت نابرابری عوض می شود :
\(a < b \Rightarrow ac\rangle bc\,\,\,\,\,,\,\,\,\,\,a < b \Rightarrow \frac{a}{c}\rangle \frac{b}{c}\)
حل نامعادله
همانند یک معادله حل میشود با این تفاوت که اگر در اخر نامعادله ضریب مجهول عدد منفی باشد جهت نامعادله عوض می شود.
مثال
مجموعه جواب نامعادله ی زیر را به دست آورده و روی محور اعداد نمایش دهید.
\(4(x - 1) \le 5x - 2\)
\(4(x - 1) \le 5x - 2 \Rightarrow 4x - 4 \le 5x - 2 \Rightarrow 4x - 5x \le 2 \Rightarrow - x \le 2 \Rightarrow x \ge - 2\)

در مسایل مربوط به نابرابری به جای کلمه حداکثر از علامت\( \le \)و به جای کلمه حداقل از علامت\( \ge \)استفاده می کنیم.
مثال
عبارت زیر را به صورت جبری بنویسید :
" مجموع دو برابر عددی با قرینه سه برابر عدد دیگر حداکثر ۹ است. "
\(2x + ( - 3y) \le - 9\)
تهیه کننده: مسعود زیرکاری



1736019749.png)