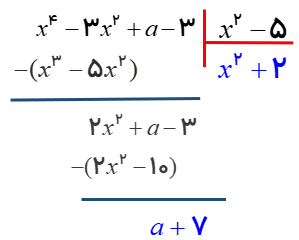درسنامه کامل ریاضی نهم فصل 7 عبارت های گویا
تعداد بازدید : 7.27Mخلاصه نکات ریاضی نهم فصل 7 عبارت های گویا - درسنامه شب امتحان ریاضی نهم فصل 7 عبارت های گویا - جزوه شب امتحان ریاضی نهم نوبت اول فصل 7 عبارت های گویا
عبارت گویا
عبارت گویا
کسری است که صورت و مخرج آن چند جمله ای باشند.
مانند :
\(\frac{{4{x^2} - 1}}{{2x + 3}},\frac{{\sqrt 5 x}}{2},\frac{{x - 3}}{x}\)
1 عبارتی که متغیر آن توان منفی یا زیر رادیکال یا داخل قدر مطلق یا در مخرج کسر یا در توان باشد. گویا نیست.
مانند :\(\left| {x - 2} \right|,\frac{{{x^y}}}{3},\frac{{4 - \sqrt x }}{{3x}}\)
2 عبارت گویا به ازای مقادیری که مخرج کسر را صفر می کند تعریف نشده است.
مثال
عبارت های گویا زیر به ازای چه مقادیری از مخرج کسر تعریف نشده است؟
\(\frac{{{x^2} - 5}}{{2x - 4}}\)
(مخرج کسر را مساوی صفر قرار داده تا مقادیر تعریف نشده مشخص شوند)
\(\frac{{{x^2} - 5}}{{2x - 4}} \Rightarrow 2x - 4 = 0 \Rightarrow 2x = 4 \Rightarrow x = 2\)
عبارت گویا به ازای (۲ = x) تعریف نشده است
\(\frac{{x - 4}}{{{x^2} - 4x}}\)
\(\frac{{x - 4}}{{{x^2} - 4x}} \Rightarrow {x^2} - 4x = 0 \Rightarrow x(x - 4) = 0 \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x - 4 = 0 \Rightarrow x = 4\end{array} \right.\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
ساده کردن عبارت گویا
ساده کردن عبارت گویا
برای ساده کردن صورت و مخرج را به صورت حاصل ضرب دو یا چند عبارت جبری نوشته سپس عبارت های مساوی را از صورت و مخرج ساده می کنیم.
برای ساده کردن عبارت های گویا از فاکتورگیری و اتحاد استفاده می کنیم.
مثال
عبارت های گویا زیر را ساده کنید.
\(\frac{{{x^2} - 4}}{{{x^2} + 2x}}\)
\(\frac{{{x^2} - 4}}{{{x^2} + 2x}} = \frac{{(x - 2)(x + 2)}}{{x(x + 2)}} = \frac{{(x - 2)}}{x}\)
\(\frac{{{x^2} - 5x + 6}}{{{x^2} - 6x + 9}}\)
\(\frac{{{x^2} - 5x + 6}}{{{x^2} - 6x + 9}} = \frac{{(x - 3)(x - 2)}}{{(x - 3)(x - 3)}} = \frac{{(x - 2)}}{{(x - 3)}}\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
ضرب و تقسیم عبارت های گویا
ضرب عبارت های گویا
در ضرب عبارت های گویا ابتدا ساده میکنیم سپس صورت در صورت و مخرج در مخرج ضرب می کنیم.
تقسیم عبارت های گویا
ابتدا تقسیم را به ضرب تبدیل میکنیم یعنی کسر اولی را در معکوس کسر دومی ضرب می کنیم.
مثال
حاصل ضرب و تقسیم عبارت های گویا زیر را به دست آورید.
\(\frac{{x + 5}}{{3x + 6}} \times \frac{{x + 2}}{{{x^2} - 25}}\)
\(\frac{{x + 5}}{{3x + 6}} \times \frac{{x + 2}}{{{x^2} - 25}} = \frac{{(x + 5)}}{{3(x + 2)}} \times \frac{{(x + 2)}}{{(x - 5)(x + 5)}} = \frac{1}{{3(x - 5)}}\)
\(\frac{{{x^2} - 2x - 15}}{{x + 3}} \div \frac{{{x^2} - x - 12}}{{2x + 6}}\)
\(\frac{{{x^2} - 2x - 15}}{{x + 3}} \div \frac{{{x^2} - x - 12}}{{2x + 6}} = \frac{{(x - 5)(x + 3)}}{{(x + 3)}} \times \frac{{2(x + 3)}}{{(x - 4)(x + 4)}} = \frac{{2(x + 5)}}{{(x - 4)}}\)
تهیه کننده: مسعود زیرکاری
جمع و تفریق عبارت های گویا
جمع و تفریق عبارت های گویا
بین مخرج ها مخرج مشترک (ک.م.م) مخرج ها را انتخاب می کنیم.
مثال
حاصل جمع و تفریق های زیر را به دست آورید.
\(\frac{{2x + 3}}{{x + 1}} + \frac{{x - 4}}{{x - 2}}\)
\(\frac{{2x + 3}}{{x + 1}} + \frac{{x - 4}}{{x - 2}} = \frac{{(2x + 3)(x - 2) + (x - 4)(x + 1)}}{{(x + 1)(x - 2)}} = \frac{{3{x^2} - 4x - 10}}{{(x + 1)(x - 2)}}\)
\(\frac{{x - 1}}{{x - 3}} - \frac{{x + 5}}{{{x^2} - 9}}\)
\(\frac{{x - 1}}{{x - 3}} - \frac{{x + 5}}{{{x^2} - 9}} = \frac{{(x - 1)(x + 3) - (x + 5)}}{{(x - 3)(x + 3)}} = \frac{{{x^2} + x - 8}}{{(x - 3)(x + 3)}}\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
ساده کردن عبارت های مرکب
ساده کردن عبارت های مرکب
عبارت صورت کسر و عبارت مخرج کسر را جداگانه جواب داده و در آخر حاصل عبارت صورت را برحاصل عبارت مخرج تقسیم می کنیم.
مثال
حاصل عبارت زیر را به ساده ترین صورت بنویسید.
\(\frac{{\frac{3}{{{x^2}}} - \frac{4}{x} + 1}}{{1 - \frac{6}{{{x^2}}} - \frac{1}{x}}}\)
\(\frac{{\frac{3}{{{x^2}}} - \frac{4}{x} + 1}}{{1 - \frac{6}{{{x^2}}} - \frac{1}{x}}} = \frac{{\frac{{3 - 4x + {x^2}}}{{{x^2}}}}}{{\frac{{{x^2} - 6 - x}}{{{x^2}}}}} = \frac{{(x - 3)(x - 1)}}{{{x^2}}} \times \frac{{{x^2}}}{{(x - 3)(x + 2)}} = \frac{{(x - 1)}}{{(x + 2}}\)
تقسیم یک جمله ای بر یک جمله ای
۱) علامت ها در هم ضرب شده
۲) اعداد با هم ساده میشوند
۳) حروف (متغیرها) با هم ساده میشوند
در ساده کردن متغیرها از قاعده تقسیم اعداد توان دار استفاده میشود
مثال
عبارت گویا زیر را ساده کنید.
\(\frac{{ - 18{x^5}{y^2}{z^4}}}{{12{x^3}{y^3}{z^4}}}\)
\(\frac{{ - 18{x^5}{y^2}{z^4}}}{{12{x^3}{y^3}{z^4}}} = \frac{{ - 18}}{{12}} \times \frac{{{x^5}}}{{{x^3}}} \times \frac{{{y^2}}}{{{y^3}}} \times \frac{{{z^4}}}{{{z^4}}} = - \frac{{3{x^2}}}{{2y}}\)
تقسیم چند جمله ای بر یک جمله ای
تک تک جملات صورت کسر را بر مخرج کسر تقسیم می کنیم.
مثال
عبارت گویا زیر را ساده کنید.
\(\frac{{4{x^5} - 6{x^3} + 12x}}{{2x}}\)
\(\frac{{4{x^5} - 6{x^3} + 12x}}{{2x}} = \frac{{4{x^5}}}{{2x}} - \frac{{6{x^3}}}{{2x}} + \frac{{12x}}{{2x}} = 2{x^4} - 3{x^2} + 6\)
تقسیم چند جمله ای بر چند جمله ای
برای این تقسیم مراحل زیر را به ترتیب انجام می دهیم :
1) ابتدا مقسوم و مقسوم علیه را به شکل استاندارد یعنی از بیشترین توان به کمترین توان می نویسیم.
۲) اولین جمله ی مقسوم را بر اولین جمله ی مقسوم علیه تقسیم کرده و حاصل را در خارج قسمت می نویسیم.
3)خارج قسمت را در تک تک جملات مقسوم علیه ضرب کرده و حاصل را زیر عبارت مقسوم نوشته و دو عبارت را از هم کم می کنیم.
۴) برای چند جمله ای به دست آمده مراحل ۲ و ۳ را تکرار کنیم و این تکرار را تا جایی ادامه میدهیم که درجه باقی مانده از درجه مقسوم علیه کمتر شود.
مثال
خارج قسمت و باقی مانده تقسیم \(4x - {x^2} + 7 + 2{x^2} \div x - 2\) زیر را به دست آورید.
مرحله اول )استاندارد کردن عبارت) \(4x - {x^2} + 7 + 2{x^2} = {x^2} - 4x + 7\)
مرحله دوم )تقسیم مقسوم بر مقسوم عليه) \(\frac{{{x^2}}}{x} = x\)
مرحله سوم (حاصل ضرب خارج قسمت در مقسوم علیه) \(x(x - 2x) = {x^2} - 2x\)
رابطه تقسیم : \((x - 2)(x + 6) + 19 = {x^2} + 4x + 7\)
اگر در تقسیم دو عبارت باقی مانده صفر .شود مقسوم بر مقسوم علیه بخش پذیر است.
مثال
مقدار a طوری بیابید که چند جمله ای ۳ - X - x + a بر ۵ – x۲ بخش پذیر باشد.
بخش پذیر بودن یعنی باقی مانده تقسیم صفر شود :\(a + 7 = 0 \Rightarrow a = - 7\)
تهیه کننده: مسعود زیرکاری



1736019749.png)