درسنامه کامل ریاضی نهم فصل 3 استدلال و اثبات در هندسه
تعداد بازدید : 7.27Mخلاصه نکات ریاضی نهم فصل 3 استدلال و اثبات در هندسه - درسنامه شب امتحان ریاضی نهم فصل 3 استدلال و اثبات در هندسه - جزوه شب امتحان ریاضی نهم نوبت اول فصل 3 استدلال و اثبات در هندسه
استدلال و اثبات در هندسه
استدلال
دلیل آوردن و استفاده از معلومات قبلی برای معلوم شدن موضوعی که در ابتدا مشخص نبوده است.
اثبات
به استدلالی که موضوع مورد نظر را به درستی نتیجه دهد اثبات می گوییم.
مثال نقض
برای رد یک ادعای ریاضی از مثال نقض استفاده می کنیم
همواره برای اثبات یک مسئله نمیتوان از رسم شکل یا شهود استفاده کرد زیرا ممکن است خطای دید در آن شکل وجود داشته باشد.
مثال
برای هر یک از مسئله های زیر یک مثال نقض بزنید :
الف تمام اشکال هندسی گوشه یا زاویه دارند؟
دایره یک شکل هندسی است که دارای گوشه و زاویه نیست.
ب تمام اعداد زوج اول هستند؟
عدد ۲ تنها عدد زوجی است که اول نیز است.
مثال
کدام یک از استدلال های زیر منطقی و کدام غیر منطقی است :
الف علی می گوید : هر وقت من درس نخواندم همان روز معلم از من سوال می کند؟
غیر منطقی
ب تصادف منجر به مرگ در جادها ممکن است به دلیل نقض فنی ماشین باشد؟
منطقی
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
فرض و حکم مسئله
فرض مسئله
اطلاعاتی که در مسئله داده شده یا حقایقی که مربوط به آن مسئله باشد. (به طور خلاصه داده ها مسئله)
حکم مسئله
خواسته های مسئله را حکم مسئله میگویند.
مثال
در هر مسئله فرض و حکم را مشخص کنید :
الف زاویه های روبه رو لوزی برابرند
فرض : خواص لوزی
حکم : برابر بودن زاویه های رو به رو
ب طول دو مماس در دایره همواره برابرند
فرض: دایره و عمود بودن خط مماس بر شعاع
حکم : برابر بودن دو مماس
مثال
با توجه به مفروضات داده شده نتیجه حاصل را بنویسید :
الف در مربع قطرها عمود منصف یکدیگرند و همچنین لوزی نوعی مربع است
در لوزی قطرها عمود منصف یکدیگرند
ب هر چهار ضلعی که زاویه قائمه داشته باشد مستطیل است و همچنین مربع دارای زاویه قائمه است
مربع نوعی مستطیل است
ثابت کنید زاویه های متقابل به راس با هم برابرند.
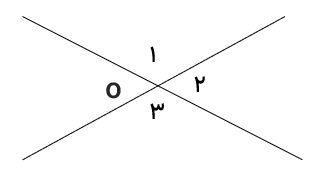
فرض : \(\widehat {{o_1}} = \widehat {{o_3}}\) دو زاویه متقابل به راس
حکم : \(\widehat {{o_1}} = \widehat {{o_3}}\)
\(\left. \begin{array}{l}\widehat {{o_1}} + \widehat {{o_2}} = 180^\circ \\\\\widehat {{o_2}} + \widehat {{o_3}} = 180^\circ \end{array} \right\} \Rightarrow \widehat {{o_1}} + \widehat {{o_2}} = \widehat {{o_2}} + \widehat {{o_3}} \Rightarrow \widehat {{o_1}} = \widehat {{o_3}}\)
ثابت کنید زاویه ی خارجی مثلث برابر است با مجموع دو زاویه ی داخلی غیر مجاور آن.
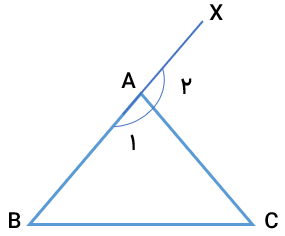
فرض : \({A_2}\) زاویه ی خارجی مثلث
حکم :\(\widehat {{A_2}} = \widehat B + \widehat C\)
\(\left. \begin{array}{l}\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \\\\\widehat {{A_1}} + \widehat B + \widehat C = 180^\circ \end{array} \right\} \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = \widehat {{A_1}} + \widehat B + \widehat C \Rightarrow \widehat {{A_2}} = \widehat B + \widehat C\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
هم نهشتی مثلث ها
هم نهشتی مثلث ها
دو مثلث به سه حالت هم نهشت هستند :
الف) دو ضلع مساوی و زاویه بین مساوی )ض ز ض)
ب) دو زاویه مساوی و ضلع بین مساوی (ز ض ز (
ج) سه ضلع مساوی (ض ض ض)
سه زاویه مساوی )ز ز ز( از حالتهای هم نهشتی نیست.
هم نهشتی دو مثلث قائم الزاویه
دو مثلث قائم الزاویه به دو حالت هم نهشت هستند :
الف) وتر و یک زاویه ی تند (و ز)
ب) وتر و یک ضلع (و ض)
نکاتی درباره هم نهشتی دو مثلث
الف) اگر دو مثلث به هم چسبیده باشند دارای ضلع مشترک هستند.
ب) اگر دو مثلث به صورت ضربدری باشند دارای زاویه متقابل به راس هستند.
ج) اگر دو مثلث داخل دایره باشند از برابری شعاع دایره استفاده می کنیم.
د) در مثلث متساوی الاضلاع هر سه ضلع و هر سه زاویه برابرند.
ه) در مثلث متساوی الساقین دو ساق و دو زاویه ی مجاور قاعده برابرند.
در دو مثلث هم نهشت اضلاع و زاویه های متناظر برابرند.
مثال
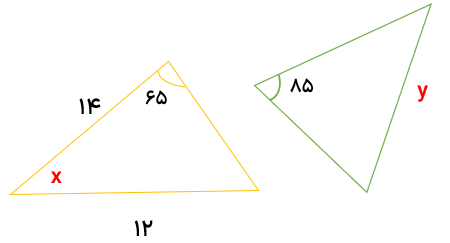
دو مثلث زیر هم نهشت هستند مقادیر مجهول را مشخص کنید.
(در دو مثلث هم نهشت اضلاع و زاویه های متناظر برابرند)
(مجوع زاویه های داخلی مثلث ۱۸۰ درجه است)
۳۰ = (۶۵ + ۸۵) - ۱۸۰
y = ۱۴ , X=30
مثال
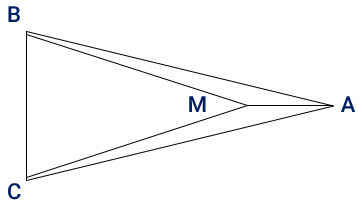
در شکل زیر دو مثلث ABC و MBC متساوی الساقین هستند دلیل هم نهشتی دو مثلث AMC و AMB را بنویسید.
فرض : AB = AC,MB = MC
حکم : \(A\mathop M\limits^\Delta B \cong A\mathop M\limits^\Delta C\)
\(\left. \begin{array}{l}AB = AC\\MB = MC\\AM = AM\end{array} \right\} \Rightarrow A\mathop M\limits^\Delta B \cong A\mathop M\limits^\Delta C\)
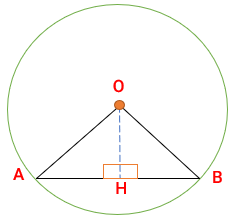
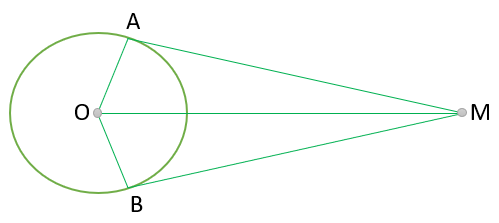
با توجه به شکل زیر نشان دهید خطی که از مرکز دایره بر وتر عمود میشود آن وتر را نصف می کند.
فرض : Oمرکز دایره و OH عمود برAB
حکم : AH = HB
\(\left. \begin{array}{l}OA = OB\\\widehat {{H_1}} = \widehat {{H_2}} = 90^\circ \\OH = OH\end{array} \right\} \Rightarrow A\mathop H\limits^\Delta O \cong B\mathop H\limits^\Delta O \Rightarrow AH = HB\)
تهیه کننده: مسعود زیرکاری
قدم های حل مسئله
قدم های حل مسئله
برای حل مسئله ۴ گام (قدم) نیاز است :
۱) درک و فهم مسئله
۲) رسم شکل
۳) نوشتن فرض و حکم مسئله
4)راهبرد حل مسئله
مثال
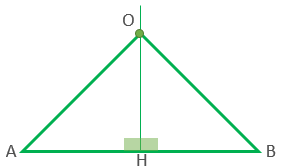
نشان دهید هر نقطه روی عمود منصف قرار داشته باشد از دو سر پاره خط به یک اندازه است.
گام اول: درک و فهم مسئله عمود منصف خطی بر خط رسم شده عمود باشد و آن خط را نصف کند.
گام دوم : (رسم شکل)
گام سوم: نوشتن فرض و حکم
فرض : OH عمود منصف
حکم : OA = OB
گام چهارم: (راهبرد حل مسئله)
هم نهشتی به طریق دوضلع و زاویه بین (ض ز ض)
\(\left. \begin{array}{l}AH = HB\\\widehat {{H_1}} = \widehat {{H_2}}\\OH = OH\end{array} \right\} \Rightarrow A\mathop H\limits^\Delta O \cong B\mathop H\limits^\Delta O \Rightarrow OA = OB\)
نشان دهید طول دو مماس رسم شده از نقطه خارج دایره با هم برابر هستند.
گام اول: (درک و فهم مسئله) شعاع دایره برخط مماس عمود و در دایره دو شعاع با هم برابرند.
گام دوم: (رسم شکل)
گام سوم : (نوشتن فرض و حکم)
فرض : \(OA = OB,\widehat A = \widehat B = 90^\circ \)
حکم : MA = MB
گام چهارم: راهبرد حل مسئله
هم نهشتی به طریق (و ض)
\(\left. \begin{array}{l}OA = OB\\\widehat A = \widehat B = 90^\circ \\OM = OM\end{array} \right\} \Rightarrow M\mathop A\limits^\Delta O = M\mathop B\limits^\Delta O \Rightarrow MA = MB\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
دو شکل متشابه
دو شکل متشابه
دو شکلی که اضلاع به یک نسبت تغییر کند )کوچک یا بزرگ یا بدون تغییر( ولی زاویه ها تغییر نکرده باشد دو شکل متشابه می گویند.
1 دو مربع دلخواه و دو مثلث متساوی الاضلاع همواره متشابه هستند.
2 دو مستطیل همواره متشابه نیست چون اضلاع ممکن است به یک اندازه تغییر نکند
3 دو لوزی دلخواه همواره متشابه نیست چون ممکن است زاویه ها دو به دو برابر نباشند
4 نسبت اضلاع متناظر دو شکل متشابه را نسبت تشابه می گویند.
5 دو شکل هم نهشت همواره متشابه و نسبت تشابه آنها عدد یک است.
مثال
دو مثلث ABC و DEF متشابه هستند اگر اضلاع مثلث ABC به اندازه های ۳ و ۴ و ۶ و اضلاع مثلث DEF به اندازه های \(x - 3,8,2y\) باشند : (اضلاع دو مثلث از کوچک به بزرگ نوشته شده اند)
الف مقدار x و y را به دست آورید.
\(\frac{3}{{2y}} = \frac{4}{8} = \frac{6}{{x - 3}} \Rightarrow \left\{ \begin{array}{l}\frac{3}{{2y}} = \frac{4}{8} \Rightarrow 8y = 24 \Rightarrow y = 3\\\\\frac{4}{8} = \frac{6}{{x - 3}} \Rightarrow 4x - 12 = 48 \Rightarrow 4x = 60 \Rightarrow x = 15\end{array} \right.\)
ب نسبت تشابه دو مثلث را بنویسید.
\(\frac{4}{8} = \frac{1}{2}\)
مثال
مقیاس نقشه ای ۱۰۰۰۰۰ : ۱ است. اگر طول جاده ای روی این نقشه ۱۲ سانتی متر باشد :
الف طول واقعی جاده چند کیلومتر است؟
\(\begin{array}{l}\frac{1}{{100000}} = \frac{{12}}{x} \Rightarrow x = 1200000cm\\\\1200000 \div 100000 = 12km\end{array}\)
تبدیل واحد : هر کیلو متر ۱۰۰۰۰۰ سانتی متر است
ب اگر اندازه ی یکی از زاویه های روی نقشه ۴۰ درجه باشد اندازه این زاویه در واقعیت چند درجه است؟
در دو شکل متشابه زاویه تغییر نمیکند پس زاویه در واقعیت نیز ۴۰ درجه است.
در دو مثلث متشابه :
الف نسبت محیط و ارتفاع و نیمساز و عمود منصف و میانه با نسبت تشابه برابر است.
ب نسبت مساحت با مجذور نسبت تشابه برابر است.
نسبت تشابه دو مثلث \(\frac{3}{5}\) می باشد :
الف نسبت میانه دو مثلث چند است؟
\(\frac{3}{5}\)
ب نسبت مساحت دو مثلث چند است؟
\({\left( {\frac{3}{5}} \right)^2} = \frac{9}{{25}}\)
تهیه کننده: مسعود زیرکاری



1736019749.png)