جواب تمرین صفحه 15 درس 1 هندسه دهم (ترسیم های هندسی و استدلال)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 15 هندسه دهم
-گام به گام تمرین صفحه 15 درس ترسیم های هندسی و استدلال
-تمرین صفحه 15 درس 1
-شما در حال مشاهده جواب تمرین صفحه 15 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
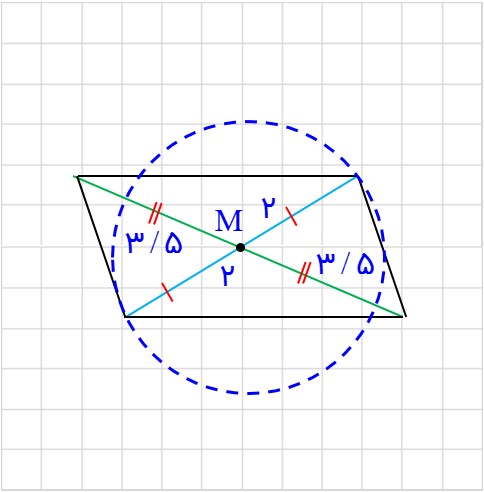
1- فرض کنیم هر چهار ضلعی که قطرهایش منصف هم باشند، متوازی الاضلاع است. متوازی الاضلاعی رسم کنید که طول قطرهای آن ٤ و ٧ باشد. چند متوازی الاضلاع به طول قطرهای 4 و 7 می توان رسم کرد؟
ابتدا یک پاره خط به طول ۷ سانتیمتر را رسم می کنیم، نقطه ی وسط آن را پیدا می کنیم و M می نامیم. دایره ای به مرکز M و شعاع ۲ سانتیمتر رسم می کنیم. یک قطر از دایره را به دلخواه رسم می کنیم. این نقطه ها را به هم وصل می کنیم، چهار ضلعی مورد نظر به دست می آید. به تعداد تمام قطرهای دایره رسم شده می توان متوازی الاضلاع به قطرهای 4 و ۷ سانتیمتر رسم کرد و چون دایره بی شمار قطر دارد، بنابراین بی شمار متوازی الاضلاع می توان رسم کرد.
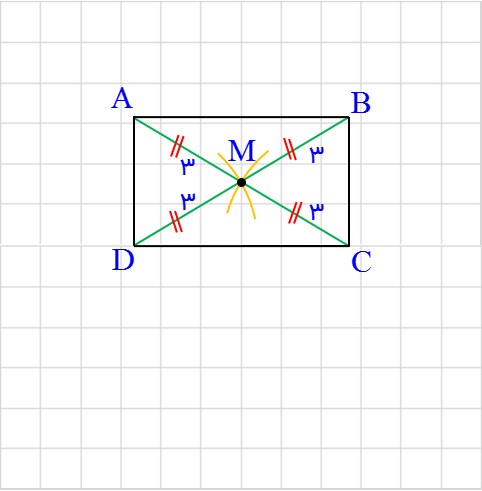
2- فرض کنیم هر چهار ضلعی که قطرهایش باهم برابر و منصف هم باشد، مستطیل است. مستطیلی رسم کنید که طول قطر آن ٦ سانتی متر باشد.
ابتدا پاره خط دلخواه AB را رسم می کنیم، مثلاً به طول ۵ سانتی متر. سپس از دو سر آن دو کمان به اندازه ی ۳ سانتی متر امتداد می دهیم و نقاط پایانی را C و D می نامیم. نقاط A و C و D و B را به هم وصل می کنیم.
3- فرض کنیم که برای لوزی بودن یک چهارضلعی کافی است که قطرهای آن چهارضلعی عمودمنصف یکدیگر باشند. ترسیم های زیر را انجام دهید.
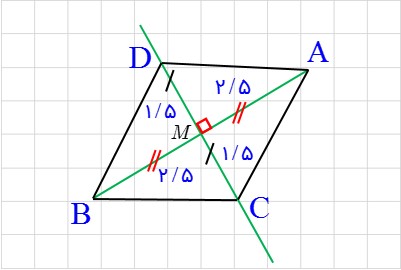
الف) یک لوزی رسم کنید که طول قطرهای آن ٣ و ٥ باشد.
ابتدا پاره خط AB به طول 5 سانتی متر را رسم می کنیم. سپس عمود منصف این پاره خط را در نقطه M که وسط پاره خط می باشد، بدست می آوریم. در نهایت یک کمان به اندازه 1/5 سانتی متر از مرکز M رسم می کنیم تا عمود منصف را در نقاط C و D قطع نماید. چهار ضلعی ABCD یک لوزی می باشد که قطرهای آن به ترتیب 5 و 3 سانتی متر می باشند.
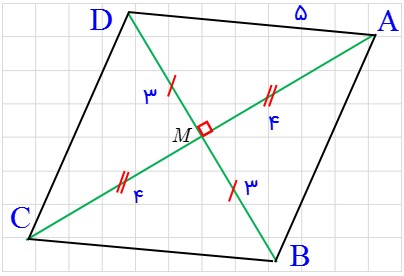
ب) یک لوزی به طول ضلع ٥ و طول قطر ٦ رسم کنید.
می دانیم در لوزی قطرها یکدیگر را نصف کرده و بر یکدیگر عمود هستند. در نتیجه یکی از اضلاع قائمه مثلث های ایجاد شده برابر نصف یک قطر یعنی 3 و وتر مثلث نیز 5 می باشد. پس ضلع قائمه دیگر مثلث طبق رابطه فیثاغورث برابر 4 می شود و بنابراین قطر دیگر لوزی دو برابر این اندازه یعنی 8 است. حال مشابه قسمت الف چهار ضلعی ABCD که لوزی مطلوب مسئله است را رسم می کنیم است.
4- دو ضلع یک زاویه را در نظر بگیرید.
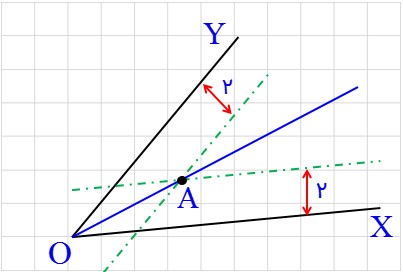
الف) نقطه ای بیابید که فاصلهٔ آن از هر ضلع زاویهٔ موردنظر 2 واحد باشد.
ابتدا از نقطه ای به فاصله 2 سانتی متر موازی محور OX ، خطی رسم می کنیم. حال همین عمل را برای محور OY انجام می دهیم. نقطه ای که از تقاطع خطوط به فاصله 2 سانتی متر از محورها بدست آمده را A می نامیم . حال از نقطه A به نقطه O رأس زاویه یک خط وصل می کنیم. این خط همان نیم ساز زاویه است، زیرا هر نقطه روی این خط به یک فاصله از محور ها هستند.
ب) با استفاده از نقطه ای که در قسمت (الف) یافته اید نیمساز زاویه را رسم کنید.
5- به قسمت (الف) پاسخ دهید و از نتیجهٔ آن در قسمت (ب) استفاده کنید.
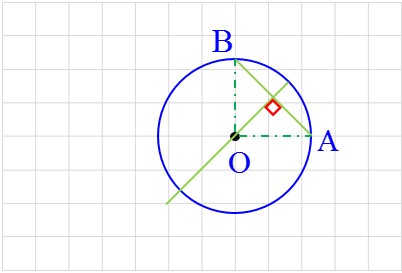
الف) وتری مانند AB از یک دایره را در نظر بگیرید. وضعیت عمودمنصف AB و مرکز دایره نسبت به هم چگونه اند؟ چرا؟
نقطه O بر روی عمودمنصف AB قرار دارد؛ زیرا دو رأس وتر بر روی کمان دایره قرار دارند و فاصله آن ها از مرکز یکسان و به اندازه شعاع است.
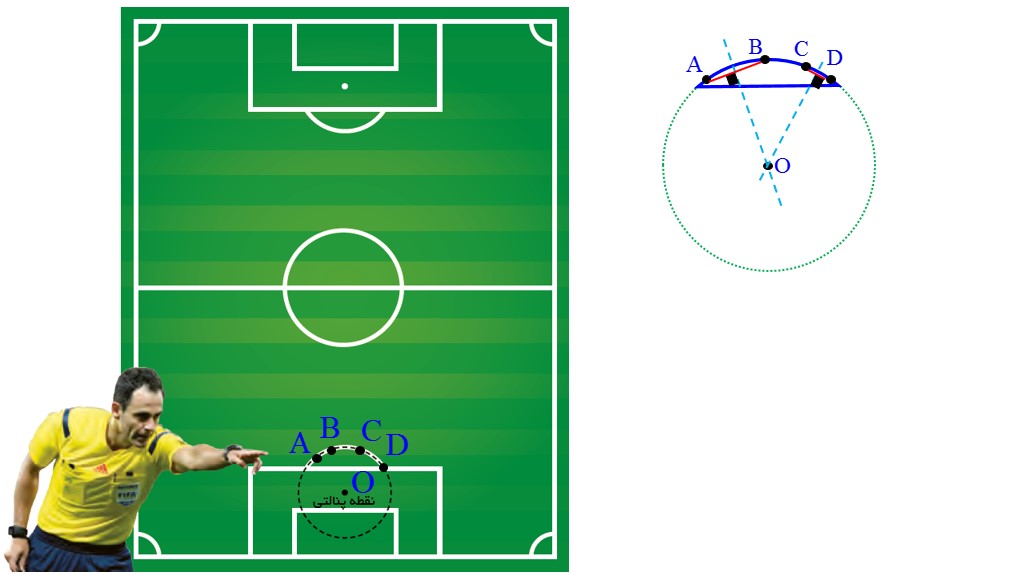
ب) آیا می دانستید که در زمین فوتبال نقطهٔ پنالتی مرکز دایره ای است که قسمتی از قوس آن در جلوی محوطهٔ جریمه کشیده شده است؟
یک داور فوتبال لحظه ای که اعلام پنالتی می کند، متوجه می شود که نقطهٔ پنالتی مشخص نیست. اگر او وسایل لازم برای کشیدن خط راست و کمان دایره را داشته باشد، چگونه می تواند با استفاده از قوس جلوی محوطهٔ هجده قدم، نقطهٔ پنالتی را مشخص کند.

نقطه پنالتی محل تقاطع دو وتر از قوس جلوی محوطه ی هجده قدم است.
کمان دایره را رسم کرده و چهار نقطه دلخواه بر روی کمان دایره مشخص می کنیم با نام های A، B، C و D. سپس وترهای AB و CD را رسم کرده و خطوط عمود منصف وارد بر آن ها را پیدا می کنیم. چون کمان دایره طوری رسم شده که اگر دایره ی کاملی بود، شعاع آن هجده قدم می شود، بنابراین خطوط عمود بر وتر یکدیگر را در نقطه O قطع می کنند. این نقطه، نقطه پنالتی خواهد بود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















