گام به گام فعّالیت صفحه 18 درس 1 هندسه (1) (ترسیم های هندسی و استدلال)
تعداد بازدید : 51.15Mپاسخ فعّالیت صفحه 18 هندسه (1)
-گام به گام فعّالیت صفحه 18 درس ترسیم های هندسی و استدلال
-فعّالیت صفحه 18 درس 1
-به استدلال هایی که دو دانش آموز برای مسئلهٔ زیر ارائه داده اند، دقت کنید و در مورد میزان اعتبار هریک از آنها گفت و گو کنید.
مسئله: مجموع زاویه های داخلی هر چهارضلعی محدب \({360^ \circ }\) است.
پژمان: در تمام چهارضلعی های مربع، مستطیل، لوزی و متوازی الاضلاع با توجه به اینکه زاویه های مجاور مکمل یکدیگرند به سادگی ثابت می شود که مجموع زوایای داخلی آنها \({360^ \circ }\) است. بنابراین مجموع زوایای داخلی هر چهارضلعی محدب \({360^ \circ }\) است.
پیمان: می دانیم مجموع زوایای داخلی هر مثلث \({180^ \circ }\) است. یک چهارضلعی دلخواه مانند ABCD در شکل مقابل را در نظر می گیریم و دو رأس مقابل آن، مثلاً D و B را به هم وصل می کنیم.
مجموع زاویه های داخلی چهارضلعی ABCD با مجموع زاویه های داخلی دو مثلث \(A\mathop B\limits^\Delta D\) و \(B\mathop C\limits^\Delta D\) برابر است؛ بنابراین مجموع زاویه های داخلی چهارضلعی ABCD برابر است با \({360^ \circ }\).
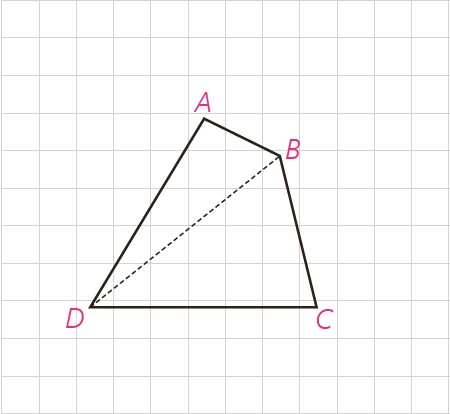
پیمان ادعا می کند که با این استدلال ثابت می شود که مجموع زاویه های داخلی هر چهارضلعی برابر \({360^ \circ }\) است.
بله؛ استدلال پیمان درست است.
آیا همین استدلال را برای هر چهارضلعی دیگری که به شما بدهند، می توانید به کار ببرید؟ اگر جواب شما مثبت است، پس این ویژگی را که «مجموع زاویه های داخلی چهارضلعی ABCD در مسئلهٔ قبل برابر \({360^ \circ }\) است«، به سایر چهارضلعی های محدب می توان تعمیم داد.
– نوع استدلال ارائه شده توسط هرکدام از دانش آموزان را بیان کنید.
نوع استدلال پژمان، استدلال استقرایی (از جزء به کل) می باشد.
نوع استدلال پیمان، استدلال استنتاجی (از کل به جزء) می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
