جواب تمرین صفحه 33 درس 1 آمار و احتمال یازدهم ریاضی (آشنایی با مبانی ریاضیات)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 33 آمار و احتمال یازدهم ریاضی
-گام به گام تمرین صفحه 33 درس آشنایی با مبانی ریاضیات
-تمرین صفحه 33 درس 1
-شما در حال مشاهده جواب تمرین صفحه 33 آمار و احتمال یازدهم ریاضی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 کدام یک از مجموعه های زیر باهم مساوی اند؟
\(\begin{array}{*{20}{l}}{A = \{ m \in \mathbb{Z}|\left| m \right| < 2\} }\\{}\\{C = \{ y \in \mathbb{Z}|{y^2} \le 2y\} }\\{}\\{E = \{ m \in \mathbb{Z}|{m^3} + 2m = 3{m^2}\} }\end{array}\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{l}}{B = \{ x \in \mathbb{Z}|{x^3} = x\} }\\{}\\{D = \{ m \in \mathbb{Z}|{m^2} \le 1\} }\\{}\\{}\end{array}\)
\(\begin{array}{*{20}{l}}{A = \{ - 1\,,\,0\,,\,1\} }\\{}\\{C = \{ 0\,,\,1\,,\,2\} }\\{}\\{E = \{ 0\,,\,1\,,\,2\} }\end{array}\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{l}}{B = \{ - 1\,,\,0\,,\,1\} }\\{}\\{D = \{ - 1\,,\,0\,,\,1\} }\\{}\\{}\end{array}\)
بنابراین نتیجه می شود که A=B=D و C=E
2 اگر دو عضو از مجموعه A حذف کنیم، تعداد زیرمجموعه های آن 384 واحد کم می شود، مجموعهٔ A چند زیرمجموعه دارد؟
گیریم مجموعه A دارای n عضو باشد در نتیجه \({2^n} - 384 = {2^{n - 2}}\) ؛ بنابراین به حل این معادله می پردازیم:
\(\begin{array}{l}{2^n} - 384 = {2^{n - 2}} \Rightarrow {2^n} - 384 = \frac{{{2^n}}}{4} \Rightarrow {2^n} - \frac{{{2^n}}}{4} = 384\\\\ \Rightarrow \frac{3}{4} \times {2^n} = 384 \Rightarrow {2^n} = 384 \times \frac{4}{3} = 512 \Rightarrow {2^n} = {2^9}\\\\ \Rightarrow n = 9\end{array}\)
مجموعه دارای 9 عضو است.
3 اگر A={2 , x+2y , 4} و B={4 , 5 , x-y} و A=B در این صورت، مقادیر x و y را بیابید.
\(\left\{ \begin{array}{l}x - y = 4\\\\x + 2y = 5\end{array} \right.\,\,\,\,\, \Rightarrow \,\,\,\,\,\left\{ \begin{array}{l}x = 3\\\\y = 1\end{array} \right.\)
4 ثابت کنید برای مجموعه های A و B با مرجع U داریم: \(A - B \subseteq A\).
\(\forall x;[x \in A - B] \Rightarrow x \in A\,,\,x \notin B \Rightarrow x \in A \Rightarrow A - B \subseteq A\)
5 فرض کنیم A و B و C سه مجموعه با مرجع U باشند، ثابت کنید: اگر \(A \subseteq B\) آن گاه:
الف \(A \cup C \subseteq B \cup C\)
می دانیم که \(A \subseteq B\) ؛ بنابراین:
\(\begin{array}{l}\forall x;(x \in A \cup C) \Rightarrow (x \in A \vee x \in C) \Rightarrow (x \in B \vee x \in C)\\\\ \Rightarrow (x \in B \cup C) \Rightarrow A \cup C \subseteq B \cup C\end{array}\)
ب \(A \cap C \subseteq B \cap C\)
می دانیم که \(A \subseteq B\)؛ بنابراین:
\(\begin{array}{l}\forall x;(x \in A \cap C) \Rightarrow (x \in A \wedge x \in C) \Rightarrow (x \in B \wedge x \in C)\\\\ \Rightarrow (x \in B \cap C) \Rightarrow A \cap C \subseteq B \cap C\end{array}\)
6 مجموعه های A و B و C و D با مرجع U را در نظر بگیرید، ثابت کنید: اگر \(A \subseteq B\) و \(C \subseteq D\) آن گاه:
الف \(A \cap C \subseteq B \cap D\)
به این دلیل که \(A \subseteq B\) و \(C \subseteq D\)، داریم:
\(\begin{array}{l}\forall x;(x \in A \cap C) \Rightarrow (x \in A \wedge x \in C) \Rightarrow (x \in B \wedge x \in D)\\\\ \Rightarrow (x \in B \cap D) \Rightarrow A \cap C \subseteq B \cap D\end{array}\)
ب \(A \cap C \subseteq B \cup D\)
به این دلیل که \(A \subseteq B\) و \(C \subseteq D\)، داریم:
\(\begin{array}{l}\forall x;(x \in A \cap C) \Rightarrow (x \in A \wedge x \in C) \Rightarrow (x \in B \wedge x \in D)\\\\ \Rightarrow (x \in B \vee x \in D) \Rightarrow (x \in B \cup D) \Rightarrow A \cap C \subseteq B \cup D\end{array}\)
7 الف فرض کنید: \(A \subseteq \emptyset \) ثابت کنید: \(A = \emptyset \).
می دانیم تهی، زیرمجموعه هر مجموعه است. بنابراین:
\(\left\{ \begin{array}{l}\emptyset \subseteq A\\\\A \subseteq \emptyset \end{array} \right. \Rightarrow A = \emptyset \)
ب فرض کنید: \(U \subseteq A\) ثابت کنید: \(A = U\).
می دانیم هر مجموعه، زیرمجموعه مجموعۀ مرجع است. بنابراین:
\(\left\{ \begin{array}{l}A \subseteq U\\\\U \subseteq A\end{array} \right. \Rightarrow A = U\)
8 هرگاه A و B دو مجموعه با مرجع U باشند و \(A \cap B = \emptyset \) در این صورت ثابت کنید:
الف \(B - A = A\)
\(\begin{array}{l}\forall x;x \in B - A \Rightarrow (x \in B \wedge x \notin A) \Rightarrow x \in B \Rightarrow B - A \subseteq B\\\\\left\{ \begin{array}{l}\forall x;x \in B\\\\A \cap B = \emptyset \end{array} \right. \Rightarrow (x \in B \wedge x \notin A) \Rightarrow x \in B - A \Rightarrow B \subseteq B - A\\\\ \Rightarrow B - A = B\end{array}\)
ب \(B \subseteq A'\)
\(\begin{array}{l}\left\{ \begin{array}{l}\forall x;x \in B\\\\A \cap B = \emptyset \end{array} \right. \Rightarrow (x \in B \wedge x \notin A) \Rightarrow x \notin A \Rightarrow x \in A'\\\\ \Rightarrow B \subseteq A'\end{array}\)
9 با استفاده از تعریف اشتراک، اجتماع و خواص جابه جایی، شرکت پذیری و توزیع پذیری برای ترکیب عطفی و فصلی در گزاره ها، هر یک از تساوی های زیر را ثابت کنید.
\(A \cap B = B \cap A\) الف
\(\begin{array}{l}A \cap B = \{ x \in U|x \in A \wedge x \in B\} = \\\\\{ x \in U|x \in B \wedge x \in A\} = B \cap A\end{array}\)
\(A \cap (B \cap C) = (A \cap B) \cap C\) ب
\(\begin{array}{l}A \cap (B \cap C) = \{ x \in U|x \in A \wedge x \in B \cap C\} = \\\\\{ x \in U|x \in A \wedge (x \in B \wedge x \in C)\} = \\\\\{ x \in U|(x \in A \wedge x \in B) \wedge x \in C\} = \\\\\{ x \in U|x \in A \cap B \wedge x \in C\} = (A \cap B) \cap C\end{array}\)
\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\) پ
\(\begin{array}{l}x \in A \cap (B \cup C) \Rightarrow x \in A \wedge x \in B \cup C\\\\ \Rightarrow x \in A \wedge (x \in B \vee x \in C)\\\\ \Rightarrow (x \in A \wedge x \in B) \vee (x \in A \wedge x \in C)\\\\ \Rightarrow (x \in A \cap B) \vee (x \in A \cap C) \Rightarrow x \in (A \cap B) \cup (A \cap C)\\\\ \Rightarrow A \cap (B \cup C) \subseteq (A \cap B) \cup (A \cap C)\end{array}\)
به طور مشابه ثابت می کنیم \((A \cap B) \cup (A \cap C) \subseteq A \cap (B \cup C)\)؛ داریم:
\(\begin{array}{l}x \in (A \cap B) \cup (A \cap C) \Rightarrow (x \in A \cap B) \vee (x \in A \cap C)\\\\ \Rightarrow (x \in A \wedge x \in B) \vee (x \in A \wedge x \in C)\\\\ \Rightarrow x \in A \wedge (x \in B \vee x \in C)\\\\ \Rightarrow x \in A \wedge x \in B \cup C \Rightarrow x \in A \cap (B \cup C)\\\\ \Rightarrow (A \cap B) \cup (A \cap C) \subseteq A \cap (B \cup C)\end{array}\)
در نهایت داریم:
\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
10 درستی هریک از تساوی های زیر را ثابت کنید.
\((A \cap B) \cup (B' \cap A) = A\) الف
\((A \cap B) \cup (B' \cap A) = A \cap (B \cup B') = A \cap U = A\)
\((A' \cap B') \cap A = \emptyset \) ب
\(\begin{array}{l}(A' \cap B') \cap A = (B' \cap A') \cap A = B' \cap (A' \cap A) = \\\\B' \cap \emptyset = \emptyset \end{array}\)
\(A \cap (B \cap C) = (A \cap B) \cap (A \cap C)\) پ
\(A \cap (B \cap C) = (A \cap A) \cap (B \cap C) = (A \cap B) \cap (A \cap C)\)
\(A \cup (B \cup C) = (A \cup B) \cup (A \cup C)\) ت
\(A \cup (B \cup C) = (A \cup A) \cup (B \cup C) = (A \cup B) \cup (A \cup C)\)
11 هر یک از عبارت های زیر را ساده کنید:
\((A' \cap B) \cup ([(B \cap A) - B'] \cap (B \cup A))\) الف
\(\begin{array}{l}(A' \cap B) \cup ([(B \cap A) - B'] \cap (B \cup A)) = \\\\(A' \cap B) \cup ([(B \cap A) \cap B] \cap (B \cup A)) = \\\\(A' \cap B) \cup ([(B \cap B) \cap A] \cap (B \cup A)) = \\\\(A' \cap B) \cup ((B \cap A) \cap (B \cup A)) = \\\\(A' \cap B) \cup ([B \cap (B \cup A)] \cap [A \cap (B \cup A)]) = \\\\(A' \cap B) \cup (B \cap A) = (A' \cap B) \cup (A \cap B) = \\\\(A' \cup A) \cap B = U \cap B = B\end{array}\)
\((A \cup B) - B\) ب
\(\begin{array}{l}(A \cup B) - B = (A \cup B) \cap B' = (A \cap B') \cup (B \cap B') = \\\\(A \cap B') \cup \emptyset = A \cap B' = A - B\end{array}\)
\([(A \cup B) - A] \cup (A \cap B)\) پ
\([(A \cup B) - A] \cup (A \cap B) = [(A \cup B) \cap A'] \cup (A \cap B) = \)
\([(A \cap A') \cup (B \cap A')] \cup (A \cap B) = \)
\(\begin{array}{l}[\emptyset \cup (B \cap A')] \cup (A \cap B) = (B \cap A') \cup (A \cap B) = \\\\(A' \cap B) \cup (A \cap B) = (A' \cup A) \cap B = U \cap B = B\end{array}\)
12 درستی هر یک از تساوی های زیر را بررسی کنید.
\((A \subseteq X) \wedge (A' \subseteq X) \Rightarrow X = U\) الف
\((A \subseteq X) \wedge (A' \subseteq X) = (A \cup A') \subseteq X \Rightarrow U \subseteq X\)
از طرفی می دانیم همواره \(X \subseteq U\)، بنابراین X=U
\((A - B) \cup (A \cap B) = A\) ب
\(\begin{array}{l}(A - B) \cup (A \cap B) = (A \cap B') \cup (A \cap B) = \\\\A \cup (B' \cap B) = A \cup \emptyset = A\end{array}\)
\((A \cap B) - C = (A - C) \cap (B - C)\) پ
\(\begin{array}{l}(A \cap B) - C = (A \cap B) \cap C' = (A \cap B) \cap (C' \cap C') = \\\\(A \cap C') \cap (B \cap C') = (A - C) \cap (B - C)\end{array}\)
\((A - B) \cup (B - A) = (A \cup B) - (A \cap B)\) ت
\((A - B) \cup (B - A) = (A \cap B') \cup (B \cap A') = \)
\([A \cup (B \cap A')] \cap [B' \cup (B \cap A')] = \)
\([(A \cup B) \cap (A \cup A')] \cap [(B' \cup B) \cap (B' \cup A')] = \)
\([(A \cup B) \cap U] \cap [U \cap (B' \cup A')] = (A \cup B) \cap (A' \cup B') = \)
\((A \cup B) - (A' \cup B')' = (A \cup B) - (A \cap B)\)
\((A \cup B) \cap (A' \cap B') = \emptyset \)ث
\(\begin{array}{l}(A \cup B) \cap (A' \cap B') = (A \cup B) - (A' \cap B')' = \\\\(A \cup B) - (A \cup B) = \emptyset \end{array}\)
\([(A \cup B) = (A \cup C) \wedge (A \cap B) = (A \cap C)] \Rightarrow B = C\) ج
\(\begin{array}{l}\left\{ \begin{array}{l}(A \cup B) = (A \cup C)\,\,\,\,\,\,\,\,\,\,(i)\\\\(A \cap B) = (A \cap C)\,\,\,\,\,\,\,\,\,\,(ii)\end{array} \right.\\\\B = B \cup (A \cap B)\mathop = \limits^{(iI)} B \cup (A \cap C) = (B \cup A) \cap (B \cup C) = \\\\(A \cup B) \cap (B \cup C)\mathop = \limits^I (A \cup C) \cap (B \cup C) = (A \cap B) \cup C\mathop = \limits^{(ii)} \\\\(A \cap C) \cup C = C\\\\ \Rightarrow B = C\end{array}\)
13 اگر A={y+2 , 5 , z} و B={x+1 , 4 , -2} در این صورت، با فرض \(A \times B = B \times A\) بیشترین مقدار برای (x+y+z) را بیابید.
از \(A \times B = B \times A\) نتیجه می شود A=B؛ بنابراین:
{y+2 , 5 , z}={x+1 , 4 , -2}
واضح است که 5 فقط می تواند با x+1 برابر باشد لذا x=4 است. اما در موارد دیگر دو حالت داریم :
\(\begin{array}{l}[(y + 2 = 4) \wedge (z = - 2)] \vee [(y + 2 = - 2) \wedge (z = 4)]\\\\ \Rightarrow [(y = 2) \wedge (z = - 2)] \vee [(y = - 4) \wedge (z = 4)] \Rightarrow y + z = 0\end{array}\)
در نتیجه x+y+z=4 خواهد بود.
14 با توجه به مجموعه های داده شده، نمودار هر یک از حاصل ضرب های \(A \times B\) و \(B \times A\) را رسم کنید.
\(A = \{ 2\,,\,3\} \,,\,B = \{ 2\,,\,3\,,\,4\} \) الف
\(\begin{array}{l}A \times B = \{ (2\,,\,2)\,,\,(2\,,\,3)\,,\,(2\,,\,4)\,,\,(3\,,\,2)\,,\,(3\,,\,3)\,,\,(3\,,\,4)\} \\\\B \times A = \{ (2\,,\,2)\,,\,(2\,,\,3)\,,\,(3\,,\,2)\,,\,(3\,,\,3)\,,\,(4\,,\,2)\,,\,(4\,,\,3)\} \end{array}\)
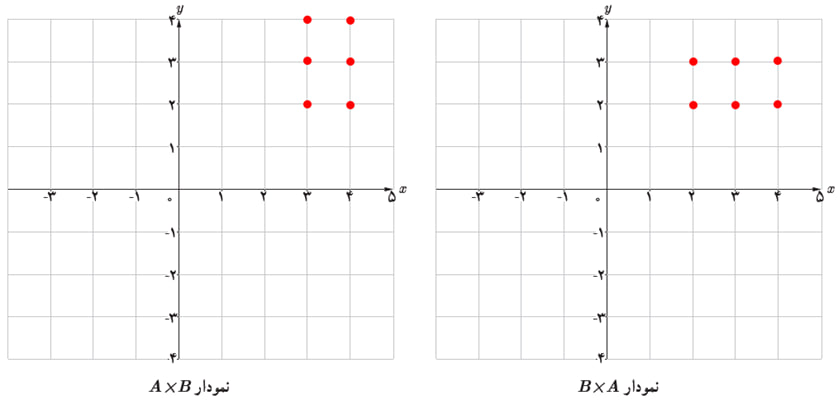
\(A = \{ 3\,,\,4\} \,,\,B = (1\,,\,5]\) ب
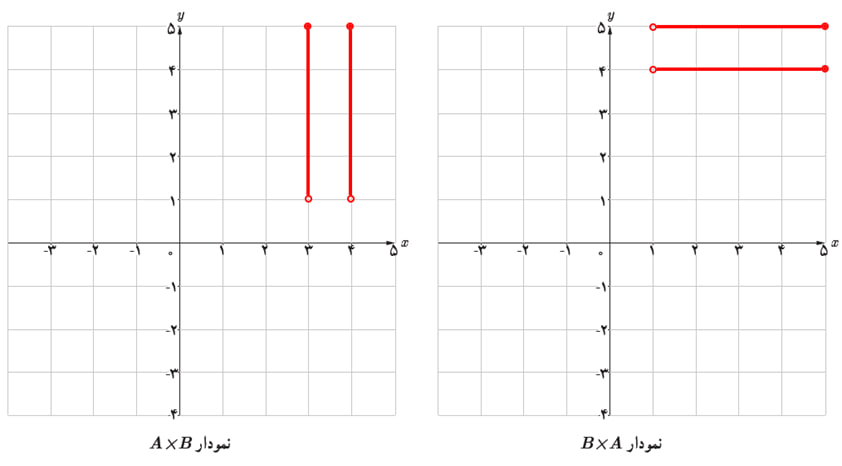
\(A = [2\,,\,6]\,,\,B = [3\,,\,8]\) پ
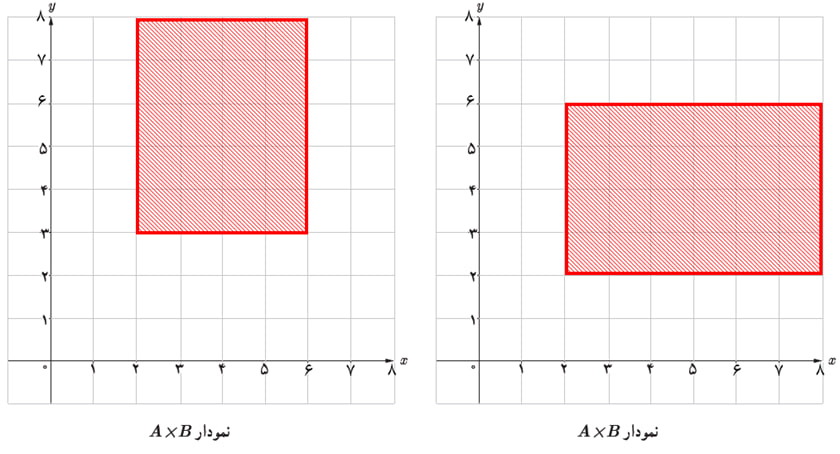
\(A = \mathbb{N}\,,\,B = [1\,,\,4]\) ت
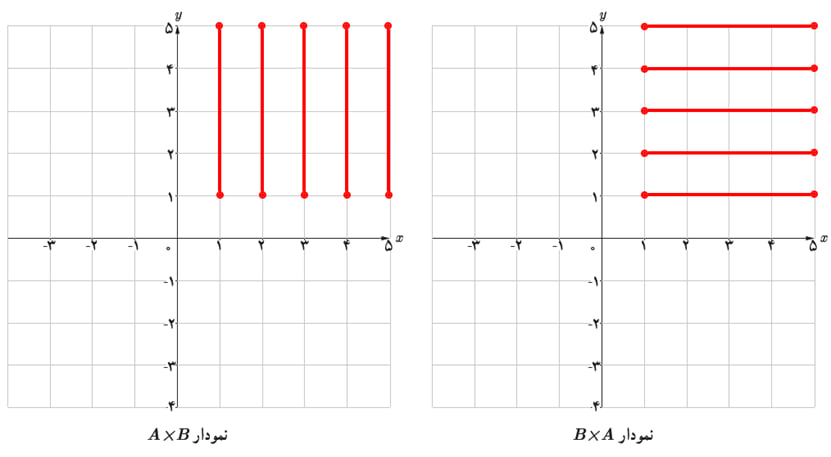
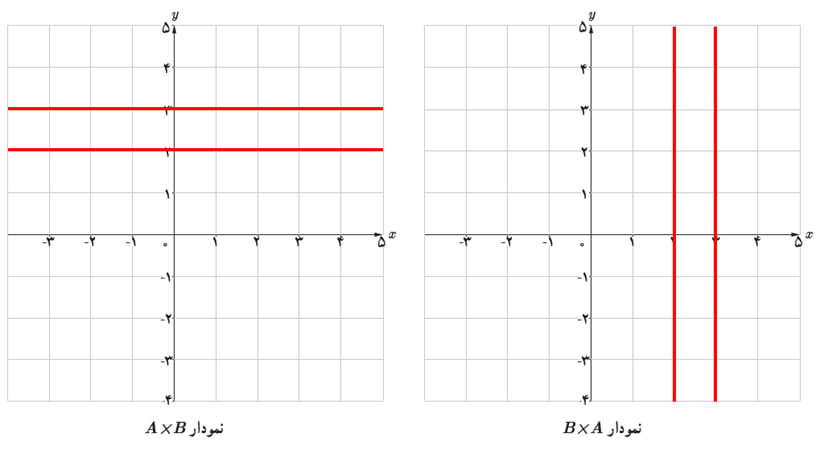
\(A = \mathbb{R}\,,\,B = \{ 2\,,\,3\} \) ث
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















