جواب فعّالیت صفحه 64 درس 3 هندسه یازدهم (روابط طولی در مثلث)
تعداد بازدید : 80.84Mپاسخ فعّالیت صفحه 64 هندسه یازدهم
-گام به گام فعّالیت صفحه 64 درس روابط طولی در مثلث
-فعّالیت صفحه 64 درس 3
-شما در حال مشاهده جواب فعّالیت صفحه 64 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
الف در مثلث ABC \(\left( {\widehat A < {{90}^\circ }} \right)\) ارتفاع BH را رسم کرده ایم. با توجه به تعریف نسبت های مثلثاتی در مثلث های قائم الزاویه، جاهای خالی را پر کنید:
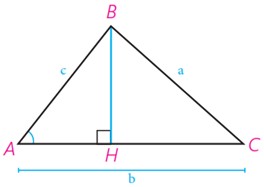
\(\begin{array}{l}\cos A = \frac{{\;....\;}}{{....}}\;\; \to \;AH = ....\; \times \;....\;\;,\\\\CH = b - Ah = ....\\\\\sin A = \frac{{\;....\;}}{{....}}\;\; \to \;BH = ....\; \times \;....\\\\\Delta BHC:B{C^2} = B{H^2} + C{H^2}\;\; \to \\\\{a^2} = {\left( {...........} \right)^2} + {\left( {...........} \right)^2}\end{array}\)
حال به کمک اتحادهای جبری و اتحاد مثلثاتی \({\sin ^2}A + {\cos ^2}A = 1\)، نشان دهید:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
ب اکنون در مثلث ABC \(\left( {\widehat A > {{90}^\circ }} \right)\) ارتفاع BH را در بیرون مثلث رسم می کنیم.
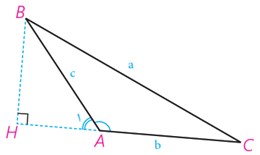
اگر A1 زاویه خـارجی رأس A باشــد با توجه به اینـکه \({\widehat A_1} = 180 - \widehat A\) داریم:
..... =sinA1 و ..... =cosA1 و در مثلث ABH نیز با توجه به تعریف نسبت های مثلثاتی می توان نوشت:
\(\begin{array}{l}\cos {A_1} = \frac{{\;....\;}}{{....}}\;,\;\sin {A_1} = \frac{{\;....\;}}{{....}}\; \to \;AH = ....\; \times \;....\;\;,\\\\BH = ....\; \times \;....\;,\;CH = b + AH = ...........\\\\\Delta BHC:B{C^2} = B{H^2} + C{H^2}\;\; \to \\\\{a^2} = {\left( {...........} \right)^2} + {\left( {...........} \right)^2}\end{array}\)
و با ساده کردن عبارت ها نشان دهید:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
سؤال: در حالتی که زاویه A قائمه باشد، این رابطه به چه صورت در می آید؟
الف
\(\begin{array}{l}\cos A = \frac{{AH}}{c}\;\; \to \;AH = c \times \cos A\;\;,\\\\CH = b - Ah = b - c \times \cos A\\\\\sin A = \frac{{BH}}{c}\;\; \to \;BH = c\; \times \;\sin A\\\\\Delta BHC:B{C^2} = B{H^2} + C{H^2}\;\; \to \\\\{a^2} = {\left( {c\; \times \;\sin A} \right)^2} + {\left( {b - c \times \cos A} \right)^2}\end{array}\)
\(\begin{array}{l}{a^2} = {(c.\sin A)^2} + (b - c.\cos A)\\\\ = {c^2}.{\sin ^2}A + {b^2} + {c^2}{\cos ^2}A - 2bc \cdot \cos A\\\\ = {b^2} + {c^2}(si{n^2}A + {\cos ^2}A) - 2bc \cdot \cos A\\\\ = {b^2} + {c^2} - 2bc \cdot \cos A\\\\ \Rightarrow {a^2} = {b^2} + {c^2} - 2bc \cdot \cos A\end{array}\)
ب
sinA=sinA1 و cosA=cosA1 و در مثلث ABH نیز با توجه به تعریف نسبت های مثلثاتی می توان نوشت:
\(\begin{array}{l}\cos {A_1} = \frac{{AH}}{c}\;,\;\sin {A_1} = \frac{{BH}}{c}\; \to \;AH = c\; \times \;\left( { - \cos A} \right)\;\;,\\\\BH = c\; \times \;\sin A\;,\;CH = b + AH = b - c \times \cos A\\\\\Delta BHC:B{C^2} = B{H^2} + C{H^2}\;\; \to \\\\{a^2} = {\left( {c\; \times \;\sin A} \right)^2} + {\left( {b - c \times \cos A} \right)^2}\end{array}\)
سؤال
\({a^2} = {b^2} + {c^2} - 2bc \cdot \cos {90^ \circ } \Rightarrow {a^2} = {b^2} + {c^2}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















