درسنامه کامل فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست - درسنامه شب امتحان فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست - جزوه شب امتحان فیزیک دوازدهم ریاضی نوبت اول فصل 1 حرکت بر خط راست
حرکت شناسی
حرکت شناسی
حركت و سكون يک امر نسبی هستند يعنی نسبت به دستگاه خاصی سنجيده می شوند هرگاه فاصله جسمی با گذشت زمان نسبت به يک مبدأ تغيير كند جسم نسبت به آن مبدأ دارای حركت می باشد.
انواع حرکت
1) حركت با سرعت ثابت (حركت يكنواخت(
2) حركت تند شونده و (شتابدار يا كند شونده(
مبدا حرکت
1) مبدأ مكان
نقطه ای اختياری بر روی محور مكان است. (\(x = 0\) )
2) مبدأ زمان
لحظه شروع حركت (\({t_0}\)) يا لحظه ای كه از آن پس حركت را بررسی می كنيم.
مکان اولیه
موضع يا مكان متحرک را در لحظه ی \({t_0} = 0\) مكان اوليه \({x_0}\) می نامند . اگر متحرک در مبدا زمان در مبدا مكان باشد مكان اوليه ی آن صفر است. (\({x_0} = 0\) )
مسیر حرکت
مكان هندسی نقاطی است كه جسم ضمن حركت از آن نقاط عبور می كند .
حرکت بر روی خط راست
در اين حركت راستای بردار جابه جايی و بردار های مكان منطبق بر مسير حركت است. بزرگی بردار مكان در هر لحظه ، فاصله ی متحرک را از مبدأ مكان نشان می دهد مطابق شكل زير مسير حركت جسمی بر روی محور xنمايش داده شده است مكان جسم در اين شكل با بردار d مشخص شده است.
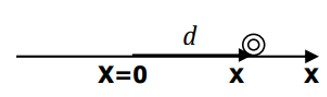
(\(d = xi\) ) بزرگی بردار مکان و(\(d = \Delta x = x - {x_0}\) )
بردار جا به جایی
بردار جابه جايی بين دو لحظه \({t_1}\) و \({t_2}\) برداری است كه ابتدای آن مكان متحرک در لحظه \({t_1}\) و انتهای آن مكان متحرک در لحظه \({t_2}\) می باشد.
بردار جابه جايی به مبدأ مكان و به شكل مسير حركت بستگی ندارد يعنی با تغيير مبدأ، تغيير نمی كند لذا نسبی نيست. (به بردار جابه جايی بردار تغيير مكان نيز می گويند.)
مكان متحرک
درحركت روی خط راست مكان متحرک عددی جبری است مانندx يا y كه جای متحرک را نسبت به مبدا مشخص می كند.
مثال
در شكل زير مسير حركت متحركی بر روی خط راست نشان داده شده است، مطلوب است:
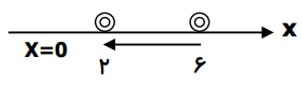
الف) رسم بردار جا به جایی
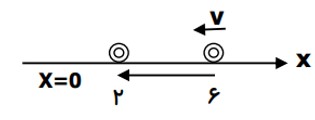
ب) محاسبه بزرگی جا به جایی
\(d = \Delta x = {x_2} - {x_1} = 2 - 6 = - 4m\)
تفاوت مسافت طی شده با جا به جایی
مسافت (L) راهی است كه متحرک می پيمايد و كميتی نرده ای است يعنی فـقط مقدار دارد (جهت ندارد) ولی جابه جايی (d) فاصله مستقيم بين مبدأ و مقصد است و كميتی برداری است.
هر گاه متحركی يک مسيری را برود و دو باره به مكان اوليه اش باز گردد ؛ جا به جايی آن صفر خواهد شد.
مثال
متحرکی از مکان \(x = - 4m\) تا مکان \(x = + 6m\) جا به جا می شود و سپس به مکان \(x = - 4m\) یر می گردد، مسافت طی شده و جا به جایی این متحرک به ترتیب چند متر است؟
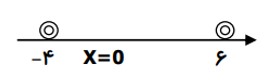
\(\begin{array}{l}L = 10 + 10 = 20m\\\Delta x = {x_3} - {x_1} = - 4 - ( - 4) = 0\end{array}\)
در حركت روی خط راست هرگاه متحرک در يک جهت حركت كند و بازگشتی وجود نداشته باشد مسافت پيموده شده با اندازه ی جابه جايی برابر است .
بازه ی زمانی
به فاصله زمانی بين دو لحظه از يک رويداد گفته می شود وبا نشان داده می شود.
مثال
متحرکی از لحظه \(t = 2s\) تا \(t = 6s\) به اندازه ی 20 مترجابه جا می شود زمان حركت (\(\Delta t\) ) چقدر بوده است؟
\(\Delta t = {t_2} - {t_1} = 4s\)
نمودار مکان-زمان
منحنی تغییرات \(x = f(t)\) نمودار مکان-زمان خوانده می شود غالباً محور افقی زمان و محور قائم مكان جسم را نشان می دهد. به كمک اين نمودار می توان مشخص کرد:
1) مكان متحرک در هر لحظه
2) مسافت
3) جا به جايی
4) مدت زمان حركت
5) تندی متوسط سرعت متوسط در هر بازه ی زمانی
6) تندی لحظه ای
7) جهت حرکت روی محور
8) علامت شتاب دار
درشكل های زير چند نمونه از اين نمودارها نشان داده شده است .
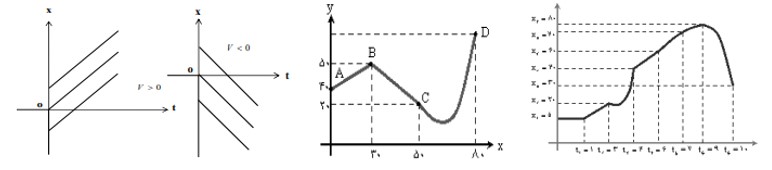
1 حركت را تعريف كنيد.
تغییر مکان یک جسم طی گذشت زمان نسبت به یک مرجع لخت، حرکت در فیزیک به معنی تغییر مکان جسم در ارتباط با زمان است .حرکت در فیزیک از نیرو ناشی می شود و با مفاهیم سرعت، شتاب، جا به جایی و زمان مرتبط است. بنا بر قانون اول نیوتن، سرعت یک جسم تنها در حالتی تغییر می کند که نیرویی به آن وارد شود.
حرکت همیشه بر اساس یک مرجع بررسی می شود و اگر مرجع ثابتی وجود نداشته باشد حرکت مطلق قابل مشاهده نیست، بنا بر همین استدلال، باید از حرکت نسبی سخن گفت. در این نگاه اگر چیزی بنا به یک مرجع ثابت باشد، به شکل نسبی در حال حرکت نسبت به مراجع دیگر است و به همین دلیل ادعا می شود که در جهان، همه چیز حرکت می کند.
2 بردار مكان چيست؟
برداری که ابتدای ان مبدا مختصات و انتهای ان مکان جسم باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تندی
تندی
تندی و سرعت متوسط
نسبت مسافت طی شده توسط متوسط تندی زمان را مدت متحرک به می گويند. و نسبت جابجايی متحرک به زمان طی شده را سرعت متوسط می گويند.
تندی متوسط (\({s_{av}} = \frac{l}{{\Delta t}}\) )
سرعت متوسط (\({v_{av}} = \frac{d}{{\Delta t}}\) )
1 سرعت متوسط كميتی برداری است در حالی كه تندی متوسط كميتی نرده ای می باشد.
2 یکای سرعت در SI متر بر ثانیه (\(\frac{m}{s}\) ) است ولی یکاهای (\(\frac{{cm}}{s}\) ) و (\(\frac{{km}}{h}\) ) نیز برای سرعت به کار برده می شوند.
3 برای تبديل واحد سرعت از متر بر ثانيه به كيلومتر بر ساعت يا بلعكس به اين صورت عمل می كنيم:
\(\begin{array}{l}\frac{{km}}{h} \div 3/6 \to \frac{m}{s}\\\frac{m}{s} \times 3/6 \to \frac{{km}}{h}\end{array}\)
تعیین سرعت متوسط به کمک نمودار مکان-زمان
سرعت متوسط بين دو نقطه از نمودار مكان-زمان برابر شيب خطی است كه آن دو نقطه را به يكديگر وصل می كند.
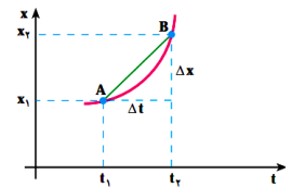
\(\frac{{\Delta x}}{{\Delta t}} = V\)
تندی لحظه ای و سرعت لحظه ای
لحظه، يعنی يک زمان بسيار كوچک
- تندی متحرک در هر لحظه از زمان را تندی لحظه ای می گويند.
- تندی كه تندی سنج اتومبيل نشان می دهد تندی لحظه ای اتومبيل می باشد.
- سرعت لحظه ای برداری است كه مماس بر مسير حركت و در جهت حركت می باشد.
1 اگر سرعت لحظه ای مثبت باشد متحرک در جهت محور مكان و اگر منفی باشد متحرک در خلاف جهت محور مكان حركت می كند.
2 هرگاه علامت سرعت عوض شود متحرک تغيير جهت می دهد و شرط اينكه متحركی نسبت به مسير اوليه خود تغيير جهت دهد (برگردد يا ساكن شود) آن است كه سرعتش صفر شود.
تعیین سرعت لحظه ای به کمک نمودار مكان-زمان
درنمودار مكان زمان شكل مقابل اگر \(\Delta t\) فوق العاده كوچک شود نقطه B خيلی به A نزديک می شود و در نهايت خط AB در نقطه A برنمودار مماس می شود.
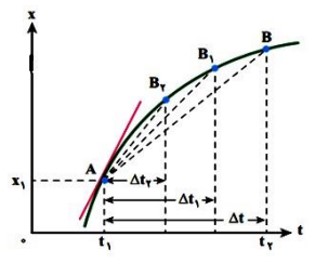
سرعت در هر لحظه برابر شیب خط مماس بر نمودار مكان– زمان در آن لحظه است.
هر گاه مماس بر نمودار مكان-زمان موازی و يا منطبق بر محور زمان باشد سرعت در آن لحظه ، برابر صفر است كه مربوط به ماكزيمم يا مينيمم منحنی است .
حرکت یكنواخت روی خط راست
هرگاه سرعت لحظه ای متحركی كه بر روی خط راست حركت می كند در تمام لحظه ها يكسان باشد، حركت آن يكنواخت ناميده می شود. در حركت يكنواخت متحرک در زمان های مساوی مسافت های مساوی را طی می كند به عبارت ديگر ، حركت يكنواخت به حركتی گويند كه در طول مسير، بردار سرعت ثابت بماند يعنی علاوه بر ثابت ماندن مقدار سرعت بايد جهت سرعت نيز ثابت بماند.
نكات مهم حرکت یكنواخت
1) در اين نوع حركت سرعت متوسط با سر عت لحظه ای برابر است. (\(V = V\) )
2) شيب نمودار مكان زمان چنين حركتی كه همان سرعت است همواره ثابت است.
3) در اين نوع حركت مكان متحرک تابعی از زمان حركت آن است: \(x = f(t)\) و اين تابع نسبت به زمان، از درجه ی اول است يعنی نمودار (مكان-زمان) آن يک خط راست است .
رابطه ی مكان زمان یا معادله حرکت
معادله حركت يک رابطه رياضی بين مكان متحرک (X) و زمانی كه متحرک به اين مكان رسيده است يعنی (t) می باشد بوسيله اين معادله می توان مكان متحرک را در هر لحظه تعيين كرد.
اگر فاصله متحرک تا مبدأ در لحظه \(t = 0\) برابر \({x_0}\) و در لحظه t برابر x باشد:
معادله حرکت یکنواخت
\(V = \frac{{\Delta x}}{{\Delta t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} \to V = \frac{{{x_2} - {x_0}}}{{{t_2} - {t_0}}} \to x = Vt + {x_0}\)
مثال
متحرکی بر روی مسیر مستقیم در مبداء زمان از نقطه (\( - 5m\) ) مطابق شکل در حال حرکت می باشد اگر سرعت آن ثابت و برابر (\(15\frac{m}{s}\) ) باشد، مکان آن را در زمان \(t = 20s\) تعیین کنید.
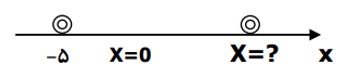
\(\begin{array}{l}x = Vt + {x_0}\\x = 15t + ( - 5) \to x = 15t - 5 \to x = 15 \times 20 - 5 = 295m\end{array}\)
نمودار سرعت-زمان
با داشتن سرعت در زمان های مختلف می توانيم اين نمودار را رسم كنيم. محور افقی را زمان و محور قائم را سرعت اختيار می كنيم.اگر متحرک با سرعت ثابت روی خط راست حركت كند نمودار سرعت زمان آن مطابق شكل مقابل خواهد بود.
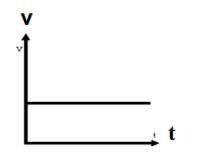
اگر سرعت متحرک ثابت نباشد نمودار سرعت زمان آن ممكن است مطابق شكل های زير باشد .

سطح محصور بين نمودار سرعت-زمان و محور زمان در بازه ی زمانی\(\Delta t\) برابر با جابه جايی متحرک (\(\Delta x\) ) است . اگر اين مساحت در بالای محور زمان باشد جابه جايی مثبت و اگر در زير محور زمان باشد جابه جايی منفی است .
1تندی متوسط و سرعت متوسط را با یکدیگر مقایسه کنید؟
تندی متوسط نسبت مسافت به زمان و کمیت نرده ای است. سرعت متوسط نسبت جا به جایی به زمان و کمیت برداری است. همچنین سرعت متوسط در یک بازه زمانی، برابر با شیب خطی است که دو نقطه نمودار مکان-زمان مربوط به ابتدا و انتهای آن بازه را به یکدیگر وصل می کند.
2در چه صورت اندازه سرعت متوسط یک متحرک با تندی متوسط آن برابر است؟
وقتی اندازه مسافت با جابه جایی برابر باشند، به عبارت دیگر اگر جهت سرعت تغییر نکند.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
شتاب
شتاب
حرکت شتابدار
در مواردی كه سرعت متحرک تغيير می كند می گوييم حركت شتاب دار يا غير يكنواخت است. يعنی ميزان جابجايی در زمان های مساوی با هم برابر نيست.
ما چه وقت احساس شتاب می كنيم؟
- زمانی كه روی پدال گاز فشار می دهيم.
- وقتی كه ترمز می كنيم.
- وقتی كه حول يک ميدان درحال دور زدن هستيم و...
در حركت شتاب دار جهت و يا اندازه سرعت و يا هر دو می تواند تغيير كند مثال درحركت بر روی مسير خميده جهت سرعت الزاما تغيير می كند يعنی در حركت بر روی مسير منحنی، حتی اگر بزرگی سرعت هم تغيير نكند حركت شتابدار است .
عوامل ایجاد کننده شتاب
1) تغيير در سرعت متحرک
2) تغيير در جهت حركت
شتاب متوسط
شتاب متوسط برابر تغيير سرعت در واحد زمان است و با \({a_{av}}\) نشان مي دهند و یکای آن (\(\frac{m}{{{s^2}}}\) ) است.
\(a = \frac{{\Delta V}}{{\Delta t}} = \frac{{{V_2} - {V_1}}}{{{t_2} - {t_1}}}\)
نکات مهم شتاب
- شتاب يک كميت برداری است. يعنی هم مقدار و هم جهت دارد.
- شتاب يعنی در هر ثانيه يک مقدار ثابت بر سرعت اضافه يا كم می شود.
- در مواردی كه بزرگی سرعت متحرک يا جهت بردار سرعت تغيير كند حركت شتاب دار است.
- در صورتی كه متحرک ساكن يا با سرعت ثابت در مسير مستقيم حركت كند شتاب آن صفر است.
- در صورتی كه سرعت متحرک مرتبا كاهش يابد يعنی ترمز كند شتاب آن منفی است.
- درفرمول شتاب هميشه سرعت نهايی ازسرعت اوليه كم می شود پس اگر \({V_2} - {V_1}\) مثبت باشد، شتاب مثبت و اگر منفی باشد شتاب منفی است.
مثال
متحركی بروی خط راست از حال سكون شروع به حركت نموده و پس از 5 ثانيه سرعتش به \(20\frac{m}{s}\) می رسد، شتاب حرکت آن را حساب کنید.
\(a = \frac{{\Delta V}}{{\Delta t}} = \frac{{V - {V_0}}}{{\Delta t}} = \frac{{20 - 0}}{5} = 4\frac{m}{{{s^2}}}\)
تعیین شتاب متوسط به کمک نمودار سرعت-زمان
شتاب متوسط بين دو لحظه برابر شيب خطی است كه نمودار سرعت زمان را در آن دو لحظه قطع می كند.
\(\alpha = a = \frac{{\Delta V}}{{\Delta t}}\)
شتاب لحظه ای
شتابی كه متحرک در هر لحظه دارد شتاب لحظه ای گويند.
شیب خط مماس بر نمودار سرعت-زمان در هر لحظه برابر شتاب لحظه ای است و هر قدر اين شيب بيشتر باشد شتاب نيز بيشتر است .
حرکت تند شونده وکند شونده
در حركت شتاب دار با شتاب ثابت روی خط راست هرگاه بردار شتاب هم جهت با بردار سرعت باشد حركت تند شونده است (\(av\rangle 0\) ) در اين نوع حركت قدر مطلق سرعت متحرک رو به افزايش می باشد و هرگاه بردار شتاب درخلاف جهت بردار سرعت باشد حركت كند شونده و قدرمطلق سرعت به تدريج كاهش می يابد: (\(av\langle 0\) )
اگر a وv هم علامت باشند حركت تند شونده در غير اين صورت حركت كند شونده است .
حرکت شتاب دار با شتاب ثابت روی خط راست
هرگاه متحركی روی خط راست حركت كند و تغيير سرعت آن در هر فاصله زمانی مساوی ، يكسان باشد شتاب متحرک ثابت است در اين نوع حركت (يعنی حركت با شتاب ثابت) شتاب متوسط بين هر دو لحظه دلخواه با شتاب متحرک در هر لحظه برابر است.
معادلات حرکت با شتاب ثابت
1) شتاب متوسط و لحظه ای
\(1)\alpha = a = \frac{{\Delta V}}{{\Delta t}}\)
2) سرعت متوسط
\(\begin{array}{l}2)V = \frac{{\Delta x}}{{\Delta t}}\\2')V = \frac{{{V_1} + {V_2}}}{2}\\2'')V = \frac{1}{2}at + {V_0}\end{array}\)
3) معادله سرعت-زمان
\(3)v = at + {v_0}\)
4) معادله مکان-زمان (معادله حرکت)
\(4)x = \frac{1}{2}a{t^2} + {v_0}t + {x_0}\)
5) معادله مستقل از زمان
\(5){v^2} - {v_0}^2 = 2a\Delta x\)
6) معادله مستقل از شتاب
\(6)\Delta x = \frac{{v + {v_0}}}{2}\Delta t\)
جا به جایی متحرک در t ثانیه n ام حرکت
اگر متحرکی با شتاب ثابت a و با سرعت اولیه \({V_0}\) روی خط راست در حال حرکت باشد جا به جایی متحرک در t ثانیه n ام حرکت از رابطه زیر بدست می آید:
\(\Delta x = \frac{1}{2}a{t^2}(2n - 1) + {V_0}t \to t = 1s \to \Delta x = \frac{1}{2}a(2n - 1) + {V_0}\)
مثال
جسمی از حال سکون با شتاب ثابت \(10\frac{m}{{{s^2}}}\) شروع به حرکت می کند، مسافت پیموده شده در ثانیه چهارم چند متر است؟
\(\begin{array}{l}{V_0} = 0\\a = 10\frac{m}{{{s^2}}}\\t = 1s\\n = 4\\\Delta x = ?\\\Delta x = \frac{1}{2}a(2n - 1) + {V_0} \to \Delta x = \frac{1}{2} \times 10 \times (2 \times 4 - 1) + 0\\\Delta x = 35m\end{array}\)
جا به جایی متحرک در n ثانیه ی آخر حرکت و در ثانیه آخر حرکت از رابطه های زیر بدست می آید:
\(\Delta x = \frac{1}{2}an(2t - n) + n{V_0} \to n = 1 \to \Delta x = \frac{1}{2}a(2t - 1) + {V_0}\)
نمودار مکان-زمان در حرکت با شتاب ثابت روی خط راست
چون معادله حركت شتابدار ثابت از درجه 2 است؛ لذا نمودار مكان-زمان آن يک سهمی است اگر دهانه نمودار به سمت بالا باشد شتاب مثبت و اگر به سمت پايين باشد شتاب منفی است. درشكل های زير چند نمونه از اين نمودارها نشان داده شده است .
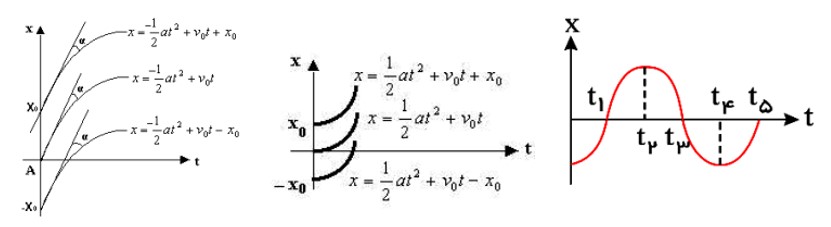
نمودار سرعت - زمان در حرکت با شتاب ثابت روی خط راست
چون معادله سرعت (\(v = at + {v_0}\) ) نسبت به زمان از درجه يک است بنابراين سرعت متحرک به طور خطی با زمان تغيير می كند يعنی نمودار سرعت-زمان اين نوع حركت به صورت يک خط راست است كه شيب آن برابر شتاب ثابت حركت است.
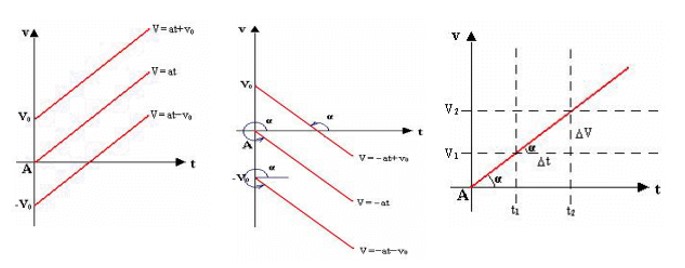
\(\alpha = a = \frac{{\Delta v}}{{\Delta t}}\)
سطح زير نمودار سرعت-زمان در حركت شتاب دار ثابت نيز اندازه جا به جايی را نشان می دهد.
نمودار شتاب-زمان
- هرنقطه از نمودار , شتاب متحرک را در يک لحظه ی دلخواه نشان می دهد.
- مساحت سطح محصور بين نمودار تا محور زمان برابر تغيير سرعت متحرک است كه اگر بالای محور زمان باشد \(\Delta v\) مثبت و اگر زير محور باشد \(\Delta v\) منفی است.
دو متحرک همزمان از یک نقطه در مسیری یکسان به حرکت در می آیند. سرعت متحرک اول در هر لحظه از متحرک دوم بیشتر است. آیا ممکن است سرعت متوسط متحرک دوم در یک بازه زمانی دلخواه بیشتر از اولی باشد؟
بله، در صورتی که مسیر خط راست نباشد؛ ممکن است جابه جایی در یک بازه زمانی برای جسم دوم بیشتر از اولی باشد و سرعت متوسط جسم دوم بزرگتر از اول شود. به عنوان مثال حرکت یک متحرک روی مسیر راست و مستقیم که برگشت هم داشته باشد، و همچنین حرکت روی مسیر دایره ای بهترین مثال ها برای توجیه این پرسش هستند. دو شناگر را تصور کنید که در مسیر رفت و برگشت یک استخر مسابقه می دهند، وقتی شناگر اول به محل اولیه برگردد سرعت متوسط آن صفر می شود در صورتی که شناگر دوم که آهسته تر حرکت می کرد سرعت متوسط آن صفر نخواهد شد.



1736019749.png)















