درسنامه کامل فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج - درسنامه شب امتحان فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج - جزوه شب امتحان فیزیک دوازدهم ریاضی نوبت اول فصل 4 برهم کنش های موج
برهم کنش موج ها
برهم کنش موج ها
مفهوم بر هم كنش موج
پديده هايی مانند بازتاب امواج، شكست موج و تداخل امواج، بر هم كنش امواج ناميده می شود.
بازتاب امواج مكانيكی در يک بعد
اگر تپی را در يک فنر (يا يک ريسمان) كشيده ی بلند كه يک سر آن بر تكيه گاهی ثابت شده است روانه كنيم، وقتی تپ به تكيه گاه (مرز) می رسد نيرويی به آن وارد می كند و طبق قانون سوم نيوتن، تكيه گاه نيز نيرويی با اندازه ی برابر و در جهت مخالف بر فنر وارد می آورد. اين نيرو در محل تكيه گاه، تپی در فنر ايجاد می كند كه روی فنر در جهت مخالف تپ تابيده حركت می كند. به مثال زير توجه كنيد:
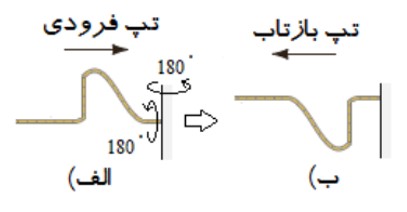
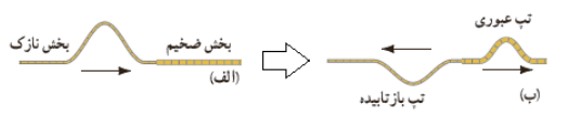
1 وقتی موجی به مرز جدايی دو محيط می رسد، بخشی از آن بازتابيده می شود و بخشی ديگر عبور می كند، به طور مثال تپ عبور در يک طناب را به صورت زير در نظر بگيريد كه از سمت نازک طناب به سمت بخش ضخيم آن در حركت است، بخشی از اين تاب بازتاب می شود و بخش ديگر عبور می كند. براي يک موج سينوسی بسامد اين دو موج همان بسامد فرودی است كه توسط چشمه ی موج تعيين می گردد، اما چون تندی آن در قسمت ضخيم كم تر است، طبق رابطه ی \(\lambda = \frac{V}{f}\) ، طول موج كم تری نسبت به موج فرودی خواهد داشت:
2 توليد صدا در آلات موسيقی، پژواک صداها، ديدن ماه، گرم شدن مواد غذايی در اجاق های خورشيدی، جمع شدن امواج راديويی در كانون آنتن های بشقابی و . . . مثال هايی از كاربرد بازتاب امواج در زندگی هستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
امواج مکانیکی
امواج مکانیکی
بازتاب امواج مكانيكی در دو بعد
امواج تختی كه بر سطح آب تشكيل می شود پس از برخورد با مانع تخت بازتاب می شوند كه اين امواج بازتابيده مانند تصاوير زير نيز تخت هستند. با استفاده از جبهه های موج می توانيم به طور تجربی به رفتار موج در برخورد با يک مانع پی ببريم:
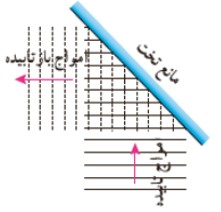
در تصوير فوق موج جبهه های موج تابيده با خطوط توپر و خطوط خط چين جبهه های موج بازتابيده را نشان می دهند.
نمودار پرتويی برای نمايش بازتاب امواج مكانيكی در دو بعد
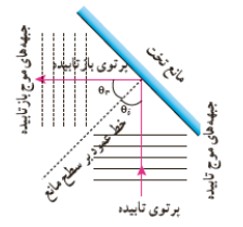
در اين نمودار يک پرتو، پيكان مستقيمی عمود بر جبهه های موج است كه جهت انتشار موج را نشان می دهد. در اين نمودار به موارد زير توجه كنيد:
1) زاويه ی تابش (\({\theta _i}\))
زاويه يی بين خط عمود بر سطح مانع و پرتوی تابيده (فرودی) زاويه ی تابش ناميده می شود.
2) زاویه بازتابش (\({\theta _r}\))
زاويه ی بين خط عمود بر سطح مانع و پرتوی بازتابيده زاويه ی تابش ناميده می شود.
3) برای امواج دايره ای و كروی همواره زاويه ی تابش و بازتابش برابر است. ( يعنی \({\theta _i} - {\theta _r}\) است كه به آن، قانون بازتاب عمومی گفته می شود(
بازتاب امواج مكانيكی در سه بعد
بازتاب امواج صوتی نمونه ای از بازتاب امواج در سه بعد است. صوت می تواند از يک مانع سخت مانند ديوار بازتاب می شود. بازتاب صوت نيز از قانون بازتاب عمومی پيروی می كند.
كاربرد بازتاب امواج صوتی در پارک های تفريحی
دو سطح كاو مانند شكل زير را در نظر بگيريد كه وقتی شخصی در كانون يكی از اين سطوح صحبت می كند، شخص ديگری در كانون سطح كاو ديگر آن را می شنود.
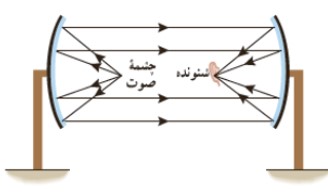
در ساخت ميكروفون سهموی كه برای ثبت صداهای ضعيف استفاده می شود و دستگاه ليتوتريپسی كه از آن برای شكستن سنگ های كليه استفاده می شود از باز تابنده های بيضوی استفاده می شود.
پژواک
اگر صوت پس از بازتاب، با يک تأخير زمانی به گوش شنونده ای برسد كه صوت اوليه را مستقيماً می شنود به چنين بازتابی پژواک می گويند. (اگر تأخير زمانی بين دو صوت كم تر از \(0/1\) ثانيه باشد گوش انسان نمی تواند پژواک صوت را از صوت اصلی تشخيص دهد)
مكان يابی پژواكی
روشی است كه بر اساس امواج بازتابيده از يک جسم، مكان آن جسم را تعيين می كند.
1 برخی جانواران نظير خفاش و دلفين از مكان يابی پژواكی استفاده می كنند.
2 در فناوری هايی نظير اندازه گيری تندی شارش خون در رگ ها، دستگاه سونار كه در كشتی ها برای مكان يابی اجسام زير آب و در سونوگرافی از مكان يابی پژواكی استفاده می شود.
3 از مكان يابی پژواكی به همراه اثر دوپلر در تعيين مكان و تعيين تندی اجسام متحرک به كار می رود.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
امواج الکترومغناطیس
امواج الکترومغناطیس
اين امواج نيز می توانند از يک سطح بازتابيده شوند و بازتاب آن ها نمونه ديگری از بازتاب در سه بعد است.
امواج الكترومغناطيسی تخت تابيده به يک سطح كاو پس از بازتابش، به يک نقطه ی كانونی می رسند. از اين ساز و كار برای دريافت امواج راديويی توسط آنتن های بشقابی و يا امواج فرو سرخ برای گرم كردن آب يا مواد غذايی در اجاق های خورشيدی استفاده می شود:
رادار دوپلری وسيله ای است كه از امواج الكترومغناطيسی براي مكان يابی پژواكی و تعيين تندی خودروها استفاده می شود.
بازتاب در نور مرئی
از آنجا كه نور مرئی نيز يک موج الكترو مغناطيس است از قانون بازتاب عمومی امواج پيروی می كند. يعنی اولاً زاويه تابش و بازتابشی با هم برابرند و ثانياً پرتوی تابش، پرتوی بازتابش و خط عمود بر سطح بازتابنده، در هر بازتابش در يک صفحه واقع اند.
انواع بازتاب نور مرئی
1) بازتاب آينه ای يا منظم
در مواردی كه سطح بازتابنده ی نور همچون يک آينه، بسيار هموار باشد، بازتاب نور را بازتاب آينه ای يا منظم می گويند.
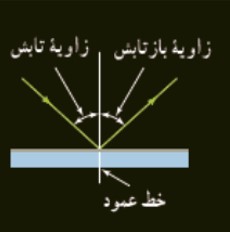
2) بازتاب پخشنده يا نامنظم
اين بازتاب وقتی رخ می دهد كه صيقلی و هموار نباشد. پرتوهای نور به طور كاتوره ای از پستی و بلندی های سطح بازتابيده، و در تمام جهات پراكنده می شود. علت ديدن اجسام رخ دادن اين نوع بازتاب است.

1 در بازتاب آينه ای از يک آينه تخت، دسته پرتوی موازی را تنها در يک جهت می توانيد ببينيد، اما در بازتاب پخشنده، اين دسته پرتو را در جهت های مختلف می توان مشاهده كرد.
2 منظور از سطح ناهموار آن است كه سطح در مقايسه با طول موج نور ناهموار است، مثلاً كاغذ در ظاهر بسيار هموار به نظر می رسد اما از ديد ميكروسكوپی اين سطح از اجزای متمايز و كوچكی تشكيل شده است كه برای يک نور مرئی ناهموار محسوب می شود.
3 برای مسائل محاسباتی مربوط به آينه های تخت به موارد زير توجه كنيد:
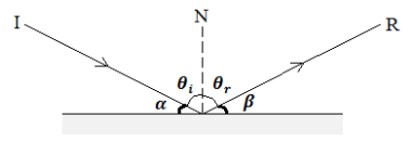
\(\begin{array}{l}{\theta _1} = {\theta _2}\\\alpha = \beta \\{\theta _1} + \alpha = 90\\{\theta _2} + \beta = 90\end{array}\)
شکست موج
شکست موج
در امواج دوبعدی (مانند امواج روی آب) و سه بعدی (امواج الكترومغناطيس) با عبور موج از يک مرز و ورود آن به محيط ديگر، تندی موج تغيير می كند و موجب تغيير جهت موج می گردد كه به آن شكست موج گفته می شود.
بررسی علت شكست موج در آب
همان طور كه قبل تر گفته شد تندی موج در سطح آب به عمق آب بستگی دارد. در تشت موج، با ورود موج به بخش كم عمق آب، تندی امواج سطحی كاهش می يابد. در حقيقت آن بخش كه زودتر به ناحيه ی كم عمق می رسد، چون با تندی كم تر حركت می كند از بقيه ی موج كه هنوز وارد اين ناحيه نشده، عقب می افتد و مطابق شكل در مرز دو ناحيه تغيير جهت می دهد. (اين مطلب را می توان در نزديک شدن امواج به يک ساحل شيب دار مشاهده كرد، درست مانند تغيير مسير يک اسباب بازی چرخ دار كه از كف صاف اتاق وارد قاليچه ای می شود(
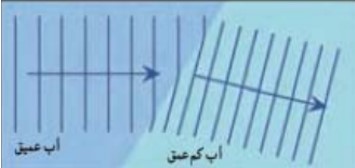
حالت های مختلف شكست با نمودار پرتويی
1) در صورتی كه موجی از محيطی با تندی كم تر به محيطی با تندی بيش تر برود زاويه ی شكست \({\theta _2}\) بزرگ تر از زاويه ی تابش \({\theta _1}\) می شود.
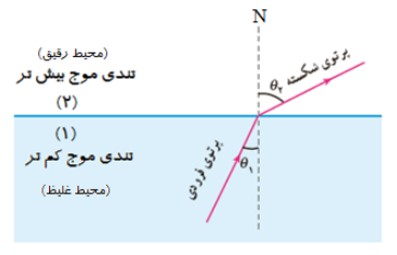
2) در صورتی كه موجی از محيطی با تندی بيش تر به محيطی با تنديی كم تر برود زاويه ی شكست \({\theta _2}\) كوچک تر از زاويه ی تابش \({\theta _1}\) می شود.
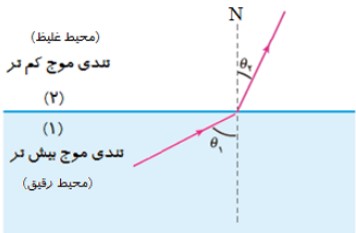
قانون عمومی شكست
نسبت سينوس زاويه شكست در محيط دوم (\({\theta _2}\)) به سينوس زاويه تابش در محيط اول (\({\theta _1}\))، برابر نسبت تندی انتشار در محيط دوم به تندی انتشار در محيط اول است:
\(\frac{{{\mathop{\rm Sin}\nolimits} {\theta _2}}}{{{\mathop{\rm Sin}\nolimits} {\theta _1}}} = \frac{{{V_2}}}{{{V_1}}}\)
ضريب شكست
برای يک پرتوی نور، نسبت تندی نور در خلأ به تندی نور در يک محیط، ضريب شكست آن محيط است:
\(n = \frac{C}{V}\)
C تندی نور در خلا (\(3 \times {10^8}\frac{m}{s}\) )
V تندی نور در يک محيط شفاف (\(\frac{m}{s}\) )
N ضريب شكست محيط شفاف
قانون شكست اسنل
رابطه ی زير كه مربوط به شكست نور و ضريب شكست است، قانون اسنل ناميده می شود:
\({n_1}{\mathop{\rm Sin}\nolimits} {\theta _1} = {n_2}{\mathop{\rm Sin}\nolimits} {\theta _2}\)
1 ضريب شكست خلأ (هوا) برابر 1 است.
2 اگر پرتو نوری به طور عمود به سطح جداكننده ی دو محيط تابش شود شكسته نمی شود.
3 هرچه محيطی متراكم تر باشد ضريب شكست آن محيط نيز بيش تر است.
4 ضريب شكست يک محيط با تندی نور در آن محيط (V) و طول موج (\(\lambda \)) رابطه ی وارونه دارد. (هر چه ضريب شكست بيش تر باشد، تندی نور و طول موج نور در آن كم تر است.)
5 بسامد، دوره تناوب و انرژی موج الكترو مغناطيس تنها به چشمه ی موج وابسته است و به ضريب شكست بستگی ندارد.
بيش تر روابطی كه در رابطه با شكست نور نوشته شده است را می توان در رابطه ی زير خلاصه نمود:
\(\frac{{{\mathop{\rm Sin}\nolimits} {\theta _2}}}{{{\mathop{\rm Sin}\nolimits} {\theta _1}}} = \frac{{{n_1}}}{{{n_2}}} = \frac{{{V_2}}}{{{V_1}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}}\)
عمق ظاهری
هنگامی كه از يک محيط شفاف به محيط شفاف ديگر نگاه می كنيم ، اجسام داخل محيط دوم در عمق بيش تر يا كم تر از مكان واقعی خود مشاهده می شوند كه در دوحالت زير می توان برای آن محاسبه انجام داد:
1) اگر ازمحيط رقيق تر به محيط غليظ تر نگاه كنيم، اجسام را در عمق كمتر از مكان واقعی خود می بينيم:
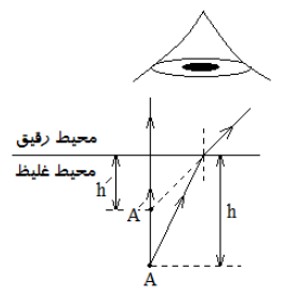
2) اگر از محيط غليظ تر به محيط رقيق تر نگاه كنيم: اجسام را در عمق می بینیم:
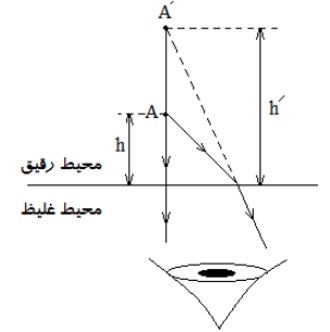
سراب
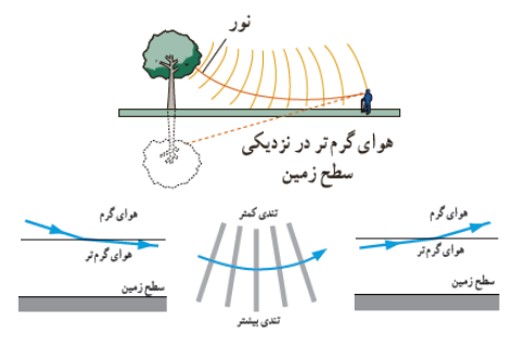
در روز های گرم، سطح زمين داغ است. از طرفی، چگالی هوا با افزايش دما كاهش می يابد كه اين سبب كاهش ضريب شكست نيز می شود. با پايين آمدن هر چه بيش تر پرتوها، آن ها با ضريب شكست كمتر و كمتری مواجه می شوند و در هر مرحله با دور شدن از خط عمود، بيشتر و بيشتر به سمت افق خم می شوند. وقتی پرتوها در نزديكی زمين تقريبا افقی می شوند، به سمت بالا خم بر می دارند زيرا بخش پايينی هر جبهه ی موج در هوای كمی گرم قرار دارد و بنابراين كمی تند تر از بخش بالايی جبهه ی موج حركت می كند و اين تفاوت رفتار دو قسمت جبهه های موج ، موجب خم شدن رو به بالای پرتوهای موج می شود، زيرا پرتوهای موج بايد همواره عمود بر جبهه های موج باشند. وقتی پرتوها رو به بالا می روند به خم شدن رو به بالای خود ادامه می دهند، زيرا اكنون مدام با محيط هايی با ضريب شكست های بزرگ و بزرگ تر مواجه می شوند و در هر مرحله با نزديک شدن به خط عمود، بيش تر و بيش تر رو به بالا خم می شوند. اگر بخشی از اين نور به چشم ما برسد، به نظر می آيد كه منشأ اين نور از امتداد رو به عقب پرتوهايی است كه به چشم ما رسيده اند و اين احساس را ايجاد می كنند كه گويی از سطح زمين آمده اند.
پاشندگی نور
وقتی باريكه ی نوری شامل پرتوهايی با طول موج های مختلف باشد، اين پرتوها هنگام عبور از مرز دو محيط در زاويه های مختلفی شكسته می شوند. به اين پخش شدگی نور، پاشندگی نور می گويند. (دليل اين پديده آن است كه ضريب شكست يک محيط برای طول موج های مختلف، يكسان نيست و هر رنگی كه طول موج كم تری دارد ضريب شكست بيش تری داشته و انحراف بيش تری پيدا می كند.) تصوير زير پاشندگی نور سفيد را در يک منشور نشان می دهد:
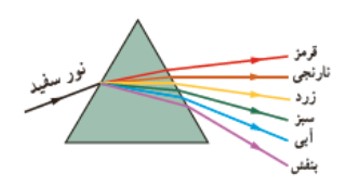
پراش موج
هنگامی كه موج از يک شكاف با پهنايی از مرتبه ی طول موج عبور می كند، به اطراف گسترده می شود، به اين پديده پراش موج گفته می شود.
1 اگر موج تختی از شكافی عبور كند كه پهنای آن خيلی بزرگ تر از طول موج باشد، آن قسمتی كه از شكاف می گذرد تقريباً تخت باقی می ماند، اما اگر موج تختی از شكافی عبور كند كه پهنای آن خيلی بزرگ تر از طول موج نباشد، آن قسمتی كه از شكاف می گذرد كاملاً از حالت موج تخت خارج شده و به مقدار بيش تری به اطراف گسترده می شود. شكل زير پراش در سه شكاف با پهناهای متفاوت را نشان می دهد:
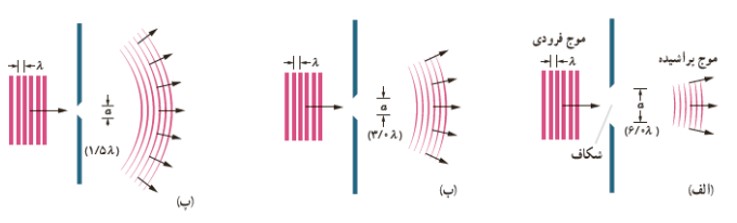
2 پراش فقط به وضعيت عبور موج از يک شكاف باريک (روزنه) محدود نمی شود بلكه هنگام عبور موج از لبه های مانعی كه ابعاد آن در حدود طول موج باشد باشد نيز رخ می دهد.
نقش پراش
اگر پراش نوری تكفام از يک شكاف باريک يا لبه ای تيز را روی يک پرده ملاحظه كنيم، همواره نوارهای تاريک و روشنی مشاهده می كنيم كه به آن نقش پراش گفته می شود. به طور مثال تصوير زير نقش پراش نوری تكفام را نشان می دهد كه از لبه های يک تيغ عبور می كند.

1 سيگنال های فرستنده های راديويی و تلويزيونی هنگام برخورد به يک مانع (مانند ديوار يا يک تپه) به دليل پراش از لبه های مانع دريافت خواهد شد. (ناحيه ای كه سيگنال به آن نمی رسد ناحيه ی سايه ناميده می شود)
2 طول موج سيگنال های فرستنده های تلويزيونی ديجيتالی امروزی كوتاه تر از طول فرستنده های قديمی است، كه اين موضوع سبب می شود پراش سيگنال ها به ناحيه ی سايه كاهش پيدا كند، زيرا همان طور كه گفته شد هرچه شكاف ها و لبه ها ابعاد بزرگتری نسبت به طول موج داشته باشد پراش كم تری رخ می دهد و گستردگی و خميدگی موج كم تر می شود.
علت خطوط تاریک در طیف نور خورشید چیست؟
طول موج مربوط به این خطوط، توسط گازهای جو خورشید و جو زمین جذب شده است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تداخل امواج
تداخل امواج
به تركيب موج ها با يكديگر تداخل می گويند.
اصل بر هم نهی امواج
وقتی چند موج به طور هم زمان بر ناحيه ای از فضا تأثير بگذارند، اثر خالص آن ها برابر مجموع اثرهای مجزای هر يک از آنها است. (به عبارت ديگر تداخل، تركيب دو يا چند موج است كه به طور هم زمان از يک منطقه عبور می كنند.)
تپ ها يا امواجی كه با يكديگر تداخل دارند به هيچ وجه شكل حركت يكديگر را تغيير نمی دهند و پس از هم پوشانی و تداخل، بدون هرگونه تغيير شكلی به حركت خود ادامه می دهند.
انواع تداخل موج
1) تداخل سازنده
اگر تپ ها در اثر هم پوشانی تپ برگتری را ايجاد كنند به آن تداخل سازنده گفته می شود.

2) تداخل ويرانگر(مخرب)
اگر تپ ها در اثر همپوشانی يكديگر را حذف كنند به آن تداخل ويرانگر گفته می شود.

تداخل امواج سطحی آب
برای مشاهده ی تداخل امواج سطحی بر سطح آب با استفاده از تشت موج، دو گوی كوچک را با بسامد يكسان، به طور هم زمان بر سطح آب به نوسان در می آوريم. دو دسته موج دايره ای ايجاد می شود كه در برخی نقاط برآمدگی ها يا فرورفتگی ها به طور هم زمان در نقطه ای به هم می رسند و همديگر را تقويت می كنند (تداخل سازنده) و اگر برآمدگی يک موج در يک زمان و در يک نقطه به فرورفتگی موج ديگر برسد، دو موج يكديگر را تضعيف می كنند (تداخل مخرب) و بنابراين سطح آب در چنين نقطه ای نوسان چندانی نخواهد داشت.

تداخل امواج صوتی
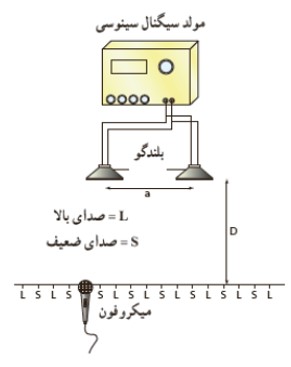
برای بررسی تداخل امواج صوتی به تصوير مقابل دقت كنيد، در اين آزمايش دو بلندگو كه به يک مولد سيگنال الكتريكی متصل اند امواج سينوسی هم بسامدی در فضا منتشر می كنند. با حركت دادن ميكروفون در امتداد خط فرضی نشان داده شده در شكل كه در فاصله ی مناسبی از بلندگوها قرار دارد در می يابيم كه بلندی صدا به طور متناوب كم يا زياد می شود. در نواحی كاهش صدا تداخل ويرانگر و در نواحی افزايش صدا تداخل سازنده رخ داده است.
تداخل امواج نوری
شخصی به نام (يانگ) با طراحی آزمايشی ثابت كرد كه بر خلاف نظر بيش تر فيزيكدانان آن زمان، نور يک موج است. شكل زير طرحی از آزمايش يانگ را نشان می دهد. نور حاصل از يک چشمه ی تكفام بر يک شكاف می تابد، سپس نور خروجی بر اثر پراش، گسترده می شود و دو شكاف و
را روشن می كند. موج های حاصل از پراش نور توسط اين دو شكاف با يكديگر تداخل می كنند و نقش حاصل از اين تداخل را می توان روی پرده ای كه در ناحيه ی سمت راست دو شكاف قرار دارد مشاهده كرد.
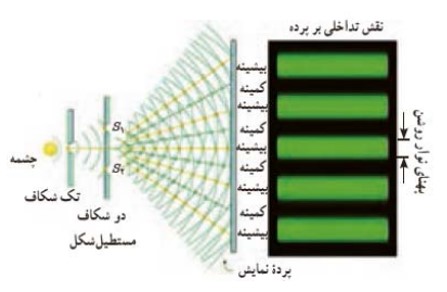
روی پرده، نقطه های با تداخل سازنده، نوارها يا فريزهای روشن را تشكيل می دهند.
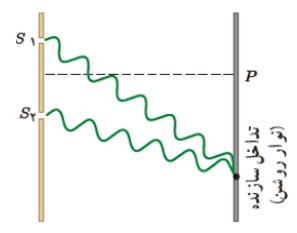
و نقطه های با تداخل ويرانگر نوارها يا فريزهای تاريک را تشكيل می دهند.
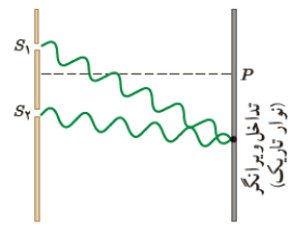
نقش تداخلی
نوارهای روشن و تاريک روی پرده كه ناشی از تداخل های سازنده و ويرانگر هستند، نقش تداخلی ناميده می شوند.
1 در نقش تداخلی پهنای نوارهای روشن و تاريک برابرند.
2 پهنای نوار های روشن و تاريک با طول موج نور به كار رفته در آزمايش رابطه ی مستقيم دارد. (يعنی هر چه طول موج به كار رفته بيش تر باشد پهنای نوارهای روشن و تاريک بيش تر است.)
3 با كمک آزمايش يانگ طول موج نور به كار رفته را می توان محاسبه نمود.
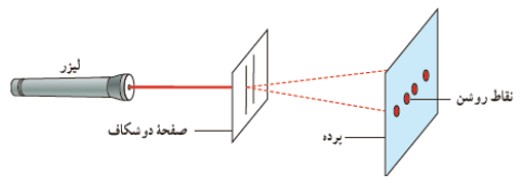
مشاهده ی نقش تداخلی به كمک نور ليزر
اگر از نور ليزر استفاده كنيم، ديگر نيازی به استفاده از يک تک شكاف در آزمايش يانگ نيست. با استفاده از يک ليزر مدادی، می توان صفحه ی دو شكاف يانگ را روشن نمود. (البته ممكن است لازم باشد از يک عدسی واگرا در برابر نور ليزر استفاده شود تا هر دو شكاف روشن گردد.)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
موج ایستاده و کشیده
موج ایستاده و کشیده
موج ايستاده و تشديد در ريسمان كشيده
هر گاه دو موج عرضی كاملاً مشابه كه در دو سوی مختلف انتشار پيدا می كنند با يكديگر تداخل نمايند، موج برايند ديگر رونده نيست و به آن موج ساكن يا ايستاده گفته می شود، كه تصوير موج برايند به شكل زير است:
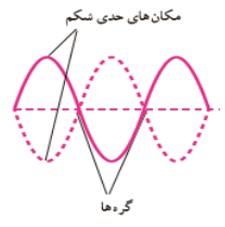
گره
نقاطی روی موج ايستاده كه هرگز نوسان نمی كنند، گره هستند. (دامنه ی نوسان صفر است)
شكم
نقاطی روی موج ايستاده كه دامنه ی موج برايند در آنجا بيشينه است. (دامنه آن ها دو برابر دامنه موج های اوليه است)
1 فاصله ی دو گره ی متوالی يا دو شكم متوالی برابر \(\frac{\lambda }{2}\) است.
2 فاصله ی يک گره از شكم مجاورش برابر \(\frac{\lambda }{4}\) است.
3 موج های تابش و بازتابش در محل گره ها با يكديگر تداخل ويرانگر انجام می دهند و در اصطلاح گفته می شود دو موج در محل گره ها كاملاً ناهمفاز (در فاز مخالف) هستند.
4 موج های تابش و بازتابش در محل شكم ها با يكديگر تداخل سازنده انجام می دهند و در اصطلاح گفته می شود دو موج در محل شكم ها در كاملاً همفاز هستند.
5 از آن جا كه موج ايستاده به چپ يا راست حركت نمی كند محل گره ها يا شكم ها ثابت است.
بسامد های تشديدی
هر گاه يک تار كشيده شده به وسيله ی يک چشمه به نوسان در آيد، به ازای بسامدهای معينی، تداخل موجب ايجاد موج ايستاده ی بارزی (يا اصطلاحاً يک مد نوسان) در تار می شود كه به اين بسامدها، بسامدهای تشديدی گفته می شود. (اگر تار در بسامدهای غير از بسامدهای تشديدی نوسان كند موج ايستاده بارزی ايجاد نمی شود.)
روابط محاسباتی موج ساكن در تار مرتعش تحت كشش
شكل زير تصاوير مربوط به حالت های مختلف موج ايستاده در يک تار است.

\(\begin{array}{l}L = n\frac{{\lambda n}}{2}\\{f_n} = n\frac{V}{{2L}} = n{f_1}\\{f_1} = \frac{V}{{2L}}\end{array}\)
(n) تعداد شكم ها(تعدادگره ها \(n + 1\) است) یا عدد هماهنگ
L طول تار
V تندي انتشار موج در طناب
\({\lambda _n}\) طول موج تشدیدی
\({f_n}\) بسامد تشدیدی
\({f_1}\) بسامد اصلی يا بسامد هماهنگ (مد) اول
1 تندی انتشار در تار مرتعش با رابطه ی \(V = \sqrt {\frac{F}{\mu }} = \sqrt {\frac{{F.L}}{m}} \) بدست می آید.
2 اختلاف بسامد دو هماهنگ متوالی در ريسمان دو انتها ثابت برابر بسامد اصلی (\({f_1}\)) است.
\({f_{n + 1}} - {f_n} = {f_1} = \frac{V}{{2L}}\)
موج ايستاده و تشديد در لوله های صوتی
در لوله های پر شده از هوا نيز می توان موج ايستاده ايجاد كرد كه به آن ها لوله های صوتی گفته می شود و در نوع دو انتها باز و يک انتها باز ساخته می شوند. وقتی موج های صوتی در هوای درون لوله حركت می كنند، از هر دو انتها باز می تابند و به درون لوله باز می گردند، حتی اگر آن انتها باز باشد (البته اگر انتهای لوله باز باشد اين بازتاب به كاملی بازتابی نيست كه از يک انتهای بسته رخ می دهد) بسياری از مشخصه های اين موج ايستاده مشابه موج ايستاده در ريسمان است؛ انتهای بسته ی لوله مانند انتهای ثابت شده ی ريسمان است كه در آنجا بايد يک گره وجود داشته باشد، و در انتهای باز لوله نيز يک شكم وجود دارد. (البته اين شكم كمی بيرون از انتهای باز لوله قرار دارد كه آن را در نظر نمی گيريم) همچنين فاصله ی گره های مجاور از هم برابر \(\frac{\lambda }{2}\) و فاصله ی گره ها از شكم های مجاور \(\frac{\lambda }{4}\) است. تصوير های زير سه مد اول را در هر دو نوع لوله نشان می دهد:
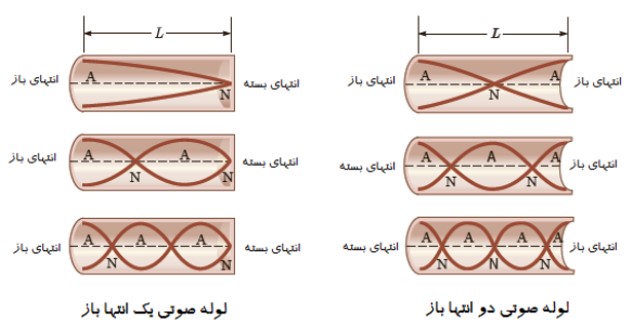
1 هر چه بسامد صوتی بيش تر می شود، آن صوت زير تر شنيده می شود و هرچه بسامد صوتی كم تر می شود آن صوت بم تر شنيده خواهد شد.
2 طول موج صوت حاصل از لوله ی صوتی با طول لوله رابطه ی مستقيم دارد. (يعنی هر چه طول لوله بيشتر باشد طول موج صوت حاصل از آن نيز بيش تر است)
3 صدای حاصل از پر شدن آب داخل يک ليوان گستره وسيعی از بسامدها را دارد كه در هر لحظه، يكی از اين بسامدها با پايين ترين بسامد تشديدی هوای درون ظرف ( بسامد مد اول) منطبق است، به همين دليل با پر شدن ليوان و كوتاه شدن فضای پر از هوای آن (كه يک لوله ی صوتی فرض می شود) طول موج صوت حاصل كاهش و بسامد آن افزايش يافته و صدا زير تر شنيده می شود.
تشديدگر هلمهولتز
كره هايی توخالي با دهانه ای باز به شكل گردن است كه همانند لوله های صوتی بسامدهای تشديدی معينی دارند و هر گاه بسامد يک صوت برابر با يكی از بسامدهای تشديديی آن ها باشد تشديدگر پاسخ قوی تری به اين صوت می دهد. (اين موضوع درست مانند دميدن در يک بطری است، در بطری نيز يكی از بسامدهايی كه هنگام دميدن توليد می شود با يكی از بسامدهای تشديدی منطبق باشد، يک موج صوتی قوی ايجاد می شود)

اجاق های ميكروموج (مايكروفر)
اين اجاق ها بر اساس تداخل امواج الكترومغناطيسی و تشكيل امواج ايستاده كار می كنند. در مورد اين وسيله به نكات زير توجه كنيد:
- ميكرو موج های بازتابيده از ديواره های فلزی اجاق با بر هم نهی با موج های تابيده (با طول موج حدود \(12cm\) ) موج های ايستاده ای را در داخل محفظه ی اجاق ايجاد می كنند كه از گره ها و شكم هايی تشكيل شده اند.
- در محل شكم ها دامنه ی نوسان ميدان الكتريكی بيشينه است. مولكول های آب موجود در مواد غذايی در اين نقاط به شدت به ارتعاش در می آيند و بيش ترين افزايش دما ايجاد می شود. (نقاط گرم)
- در محل گره ها دامنه نوسان صفر است و غذا گرم نمی شود. (نقاط سرد)



1736019749.png)















