درسنامه کامل فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای - درسنامه شب امتحان فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای - جزوه شب امتحان فیزیک دوازدهم ریاضی نوبت اول فصل 2 دینامیک و حرکت دایره ای
دینامیک
دینامیک
ديناميک به بررسی علت حركت می پردازد.
ويژگی های نيرو:
- نيرو حاصل بر هم كنش يا اثر متقابل دو جسم بر يكديگر است.
- نيرو كميتی برداری است كه يكای آن نيوتن (N) است.
- اثر نيرو بر يک جسم به شكل های مختلف مانند شروع به حركت كردن، توقف، كم و زياد شدن اندازه ی سرعت، تغيير جهت سرعت و تغيير شكل جسم ، خود را نشان می دهد.
محاسبه نیروی خالص
1) اگر دو بردار با يكديگر هم جهت باشند؛
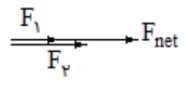
\(1){F_{net}} = {F_1} + {F_2}\)
2) اگر دو بردار خلاف جهت يكديگر باشند؛
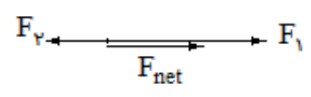
\(2){F_{net}} = \left| {{F_1} - {F_2}} \right|\)
3) اگر دو بردار عمود بر هم باشند؛
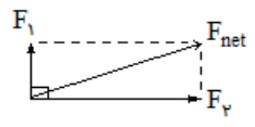
\(3){F_{net}} = \sqrt {F_1^2 + F_2^2} \)
4) اگر دو بردار هم اندازه و عمود بر هم باشند؛
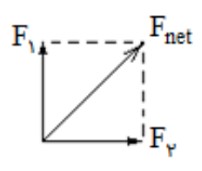
\(4){F_{net}} = \sqrt 2 {F_1}\)
روش حل مسائل ديناميک
به ترتيب زير عمل كنيد:
- رسم تمام نيروهای وارد بر جسم.
- انتخاب محورهای مختصات مناسب (در صورتی كه حركت شتاب دار باشد بهتر است يكی از محورها در جهت شتاب حركت باشد)
- نوشتن قانون اول يا دوم نيوتن روی محور های x و y به طور جداگانه و حل مسأله.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قوانین حرکت نیوتون
قوانین حرکت نیوتون
1) قانون اول نیوتون
يک جسم، حالت سكون يا حركت با سرعت ثابت خود را حفظ می كند مگر آنكه نيروی خالص غير صفری به آن وارد شود.
به عبارت ديگر:
\({F_{net}} = 0\) اگر جسم ساکن باشد یا حرکت یکنواخت روی خط راست انجام دهد.
اگر به جسمی به طور هم زمان چند نيرو اثر كند و اين نيرو ها اثر يكديگر را خنثی كنند ( برآيند نيروها صفر باشد) می گوييم نيروهای وارد بر جسم متوازن است.
لختی
هنگامی كه نيروی خالص وارد بر جسم صفر باشد، جسم حالت سكون يا حركت يكنواخت خود را حفظ می كند، به اين خاصيت لختی گفته می شود.
2) قانون دوم نیوتون
هر گاه برجسمی نيروی خالصی وارد شود، جسم تحت تأثير آن نيرو شتاب می گيرد كه اين شتاب با نيروی خالص وارد بر جسم نسبت مستقيم دارد و در همان جهت نيروی خالص است و با جرم جسم نسبت وارون دارد:
\({F_{net}} = ma\) اگر جسم حرکت شتاب دار داشته باشد. (سرعت جسم تغییر کند)
بر اساس قانون دوم نيوتن می توان گفت جهت بردار شتاب يک جسم ، هم جهت با برآيند نيروهای وارد بر جسم است.
3) قانون سوم نیوتون
هرگاه جسمی به جسم ديگر نيرو وارد كند، جسم دوم نيز به جسم اول نيرويی هم اندازه و هم راستا در خلاف جهت وارد می كند. (نيروها ی كنش و واكنش با هم برابرند و درخلاف جهت يكديگر)
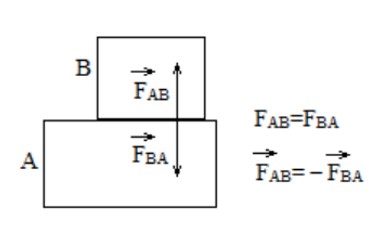
1 نيروی كنش و واكنش به دو جسم وارد می شود و برآيند گيری از آن ها اشتباه است.
2 نيروی كنش و واكنش اثرهای يكسانی بر اجسام ندارند.
3 نيروی كنش و واكنش هم نوعند.
دو شخص به جرم هاي \(75Kg\) و یا \(50Kg\) با كفش های چرخ دار در يک سالن مسطح و صاف روبه روی هم ايستاده اند. شخص اول با نيروي \(120N\) شخص دوم را به طرف راست هل می دهد، اگر اصطكاک قابل چشم پوشی باشد،
الف) شتاب که شخص دوم چند \(\frac{m}{{{s^2}}}\) می شود؟
\({F_{12}} = {m_2}{a_2} \to {a_2} = \frac{{{F_{12}}}}{{{m_2}}} \to {a_2} = \frac{{120}}{{50}} \to {a_2} = 2/4\frac{m}{{{s^2}}}\)
ب) جهت شتاب شخص اول چقدر و به كدام سمت است؟
\(\begin{array}{l}{F_{12}} = - {F_{21}}\\{a_1} = \frac{{ - {F_{21}}}}{{{m_1}}} \to {a_1} = \frac{{ - 120}}{{75}}i \to {a_1} = - 1/6\frac{m}{{{s^2}}}i\end{array}\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
برخی از نیرو های خاص
نیروی وزن
وزن يک جسم روی زمين ، نيروی گرانشی است كه از طرف زمين بر جسم وارد می شود، كه به صورت زير قابل محاسبه است:
\(W = mg\)
1 جهت نيروی وزن و شتاب گرانشی همواره به طرف مركز زمين است.
2 جرم يک جسم در مكان های مختلف ثابت است اما وزن آن به مقدار g در آن مكان بستگی دارد.
نیروی عمودی سطح
نيرويی كه از طرف سطح به اجسام روی آن و به صورت عمود بر سطح وارد می شود، نيروی عمودی سطح (نيروی عمودی تكيه گاه) ناميده می شود. (این نیرو با \({F_N}\) نمایش داده می شود)
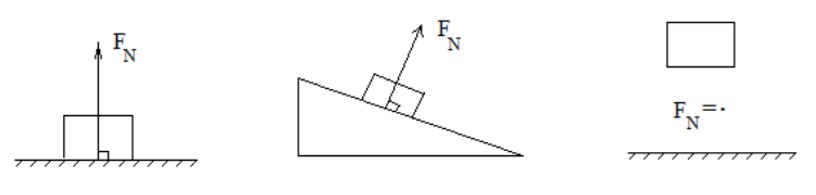
نيروی عمودی سطح ناشی از تغيير شكل سطح تماس دو جسم است. (هنگامی كه اجسام روی سطوح بسيار سخت قرار می گيرند سطح مانند اسفنج تغيير شكل دارد. اين تغيير شكل مربوط به نيروهای بين مولكولی است)
نیروی اصطکاک
وقتی تلاش می كنيم جسمی را روی سطحی به حركت در آوريم، چه جسم حركت كند و چه ساكن بماند، با مقاومتی از طرف سطح روبه رو می شويم كه به آن نيروی اصطكاک می گوييم.
انواع نیروی اصطکاک
الف) نيروی اصطكاک ايستايی (\({f_s}\))
هنگامی كه نيرويی برای حركت دادن جسم روی سطح وارد می شود، اما جسم حركت نكند، نيرويی كه از طرف سطح در مقابل حركت وارد می شود ، نيروی اصطكاک ايستايی ناميده می شود:
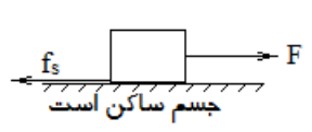
\({f_s} = F\)
ب) نیروی اصطکاک در آستانه ی حرکت (\({f_{s\max }}\) )
اين نيرو، نوعی نيروی اصطكاک ايستايی است، هنگامی كه نيرويی بر جسم وارد شود و آن را در آستانه ی حركت قرار دهد (يعنی جسم هنوز شروع به حركت نكرده است اما با تغيير ناچيزی در شرايط جسم شروع به حركت كند)، نيرويی كه در برابر حركت جسم مقاومت می كند، نيروی اصطكاک در آستانه ی حركت ناميده می شود و در واقع اين نيرو بيشينه ی نيروی اصطكاک ايستايی است:
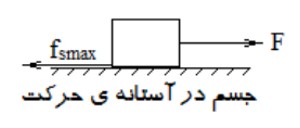
\(\begin{array}{l}{f_{s\max }} = F\\{f_{s\max }} = {\mu _s}{F_N}\end{array}\)
\({\mu _s}\) ضریب اصطکاک ایستایی
\({F_N}\) نیروی عمودی تکیه گاه
طراحی آزمايش برای تعيين ضريب اصطكاک ايستايی جسم با سطح:
ابتدا مانند تصوير به نيروسنج متصل به جسم را به تدريج می كشيم تا جسم در آستانه حركت قرار گيرد. (يعنی با ضربه كوچكی شروع به حركت نمايد)

در اين لحظه عدد نيرو سنج را می خوانيم در اين وضعيت عددی كه نيروسنج نشان می دهد (F) همان نيروی اصطكاک آستانه حركت (\({f_{s\max }}\) ) است. با رابطه زير ضريب اصطكاک ايستايی را محاسبه می كنيم:
\({f_{s\max }} = F \to {\mu _s}{F_N} = F \to {\mu _s}mg = F \to {\mu _s} = \frac{F}{{mg}}\)
پ) نیروی اصطکاک جنبشی (\({f_K}\) )
نيرويی است كه از طرف سطح در خلاف جهت حركت بر اجسام متحرک وارد می شود:
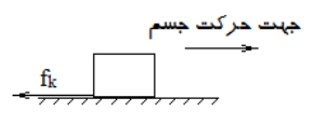
\({f_K} = {\mu _K}{F_N}\)
\({\mu _K}\) ضریب اصطکاک جنبشی
\({F_N}\) نیروی عمودی تکیه گاه
1 ضريب اصطكاک ايستايی (\({\mu _s}\) ) و ضريب اصطكاک جنبشی (\({\mu _K}\) ) به مشخصات فيزيكی دو سطح تماس (مانند جنس دو سطح تماس، ميزان صافی يا زبری آن ها و . . . )بستگی دارند.
2 برای دو سطح تماس معين \({\mu _K} \le {\mu _s}\) و \({f_K} \le {f_{s\max }}\) است.
3 نمودار نيروی اصطكاک بر حسب نيرويی كه جسم را می كشد به صورت زير است:
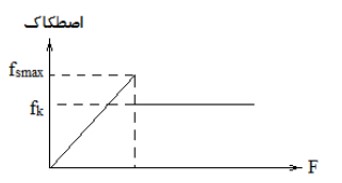
در مسائلی كه مشخص نيست جسم ساكن است يا متحرک، ابتدا با رابطه ی \({f_{s\max }} = {\mu _s}{F_N}\) ، بيشينه ی اصطكاک ايستايی را محاسبه می كنيم و سپس آن را با نيروی كشش وارد بر جسم (نيروی خلاف جهت اصطكاک) مقايسه می كنيم و به موارد زير توجه می كنيم:
- اگر نيروی كشش بزرگتر از \({f_{s\max }}\) باشد، آنگاه جسم حرکت می کند و در نتیجه اصطکاک سطح از نوع \({f_K}\) است.
- اگر نيروی كشش کوچکتر از \({f_{s\max }}\) باشد، آنگاه جسم ساکن است و در نتیجه اصطکاک سطح از نوع \({f_s}\) است.
- اگر نيروی كشش برابر با \({f_{s\max }}\) باشد، آنگاه جسم در آستانه ی حرکت است و در نتیجه اصطکاک سطح از نوع \({f_{s\max }}\) است.
نیروی واکنش سطح
برآيند نيروهايی كه از طرف سطح به جسم وارد می شوند (برآيند نيروی اصطكاک و نيروی عمودی تكيه گاه) نيروی واكنش سطح ناميده می شود:
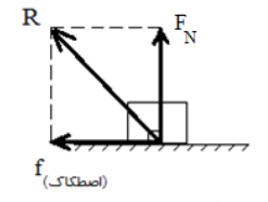
\(R = \sqrt {f_{fri}^2 + F_N^2} \)
(fri) بخشی از کلمه (Friction) به معنای اصطکاک است.
نیروی مقاومت شاره
وقتی جسمی در يک شاره (مايع يا گاز) قرار دارد و نسبت به آن حركت می كند از طرف شاره نيرويی در خلاف جهت حركت جسم ، به آن وارد می شود كه به آن نيروی مقاومت شاره می گويند و معمولاً آن را با \({f_D}\) نشان می دهند.
1 نيروی مقاومت شاره به بزرگی جسم، تندی آن و . . . بستگی دارد و هر چه اندازه جسم بزرگتر باشد يا تندی آن بيش تر شود نيروی مقاومت شاره نيز بيش تر می شود.
2 اگر جسم در هوا حركت كند، به جای نيروی مقاومت شاره ، اصطلاح نيروی مقاومت هوا به كار برده می شود.
تندی حدی
هنگام سقوط آزاد جسمی مانند چتر نجات يا قطرات باران، تندی جسم كاهش می يابد تا اينكه نيروی مقاومت هوا با وزن جسم هم اندازه شده و پس از آن جسم با تندی ثابتی به طرف پايين حركت می كند. به اين تندی ثابت تندی حدی گفته می شود.
نیروی شناوری
نيروی بالا سويی كه از طرف شاره به جسم شناور يا غوطه ور در شاره وارد می شود، نيروی شناوری گفته می شود که با \({F_b}\) نشان می دهند.
نیروی کشسانی فنر
اگر فنر را بكشيم يا فشرده كنيم، فنر نيرويی به طرف نقطه ی تعادل به جسم وارد می كند كه به آن نيروی فنر گفته می شود و با \({F_e}\) نمايش داده می شود كه جهت آن از جسم به سمت بيرون و در راستای فنر است و با رابطه ی زير محاسبه می گردد:
\({F_e} = k\Delta x\)
K ثابت فنر یا ضریب سختی فنر (\(\frac{N}{m}\) )
\(\Delta x\) تغییر طول فنر (m)
قانون هوک
نسبت نيروی وارد شده به فنر به تغيير طول آن همواره مقدار ثابتی است.
عوامل مؤثر بر ضريب سختی فنر عبارتند از:
- اندازه فنر
- شکل فنر
- جنس فنر
در نمودار نيروی فنر بر حسب تغيير طول فنر هر چه شيب نمودار بيش تر باشد ثابت فنر بيشتر و فنر سخت تر است.
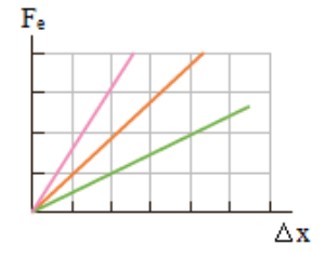
طراحی آزمايش برای تعيين ضريب سختی فنر
فنری با طول اوليه مشخص را مانند تصوير از يک نقطه به طور قائم آويزان می كنيم و به سر ديگر آن جسمی به جرم m وصل می كنيم. پس از رسيدن فنر به حالت تعادل ، تغيير طول فنر (\(\Delta x\) ) را حساب كرده و از رابطه زير ثابت فنر به دست می آيد:
\(K\Delta x = mg \to K = \frac{{mg}}{{\Delta x}}\)
نیروی کشش طناب
هنگامی كه با يک طناب جسمی را می كشيم ، طناب نيز با نيرويی جسم را می كشد كه به آن نيروی كشش ريسمان گفته می شود و جهت آن از جسم به سمت بيرون و در راستای طناب است و اين نيرو با نماد T نشان داده می شود.
تمرین
1فنری به طول \(20cm\) و ثابت\(40\frac{N}{{cm}}\) را از سقف یک آسانســور آویزان کرده و جسمی به جرم \(2Kg\) را به انتهای فنـر وصل می کنیم. اگر آسانسور با شتاب ثابت \(2\frac{m}{{{s^2}}}\) به طرف بالا شروع به حرکت کند، طول فنر چند سانتی متر می شود؟ (\(g = 10\frac{m}{{{s^2}}}\) )
\(\begin{array}{l}{F_e} - mg = ma \to kx = m(g + a) \to 40x = 2 \times 12\\x = \frac{{24}}{{40}} = 0/6cm \to x = {L_2} - {L_1} \to {L_2} = x + {L_1} \to {L_2} = 20/6cm\end{array}\)
2جسمی به جرم \(200Kg\) روی زمین قرار دارد. جسم را توسط یک نیروی افقی به طرف راست می کشیم. اگر ضریب اصطکاک جسم با زمین \(0/3\) ، نیروی مقاومت هوا در برابر حرکت 300 نیوتن و شتاب حرکت جسم \(2\frac{m}{{{s^2}}}\) باشد، نیروی افقی چند نیوتن است؟ (\(g = 10\frac{m}{{{s^2}}}\) )
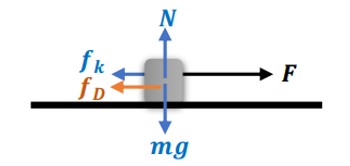
\(\begin{array}{l}{f_k} = {\mu _k}{F_N} = {\mu _k}mg = 0/3 \times 2000 = 600N\\F - {f_D} - {f_k} = ma \to F = ma + {f_D} + {f_k}\\F = 400 + 300 + 600 = 1300N\end{array}\)
مسائل آسانسور
مسائل آسانسور
در اينگونه مسائل بايد توجه داشته باشيد كه شتاب اجسام داخل آسانسور همان شتاب خود آسانسور است، به مثال های زير كه برای كابل آسانسور نوشته شده است توجه كنيد: ( توصيه می كنيم كه جهت محور y را جهت شتاب آسانسور فرض كنيد)
1) اگر شتاب آسانسور رو به بالا باشد:
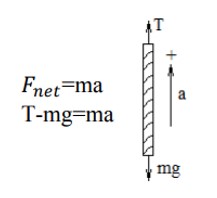
2) اگر شتاب آسانسور رو به پايين باشد:
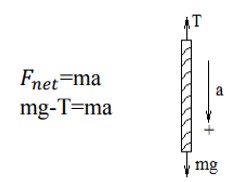
وزن ظاهری اجسام داخل آسانسور
نيروی عمودی تكيه گاه (\({F_N}\) ) كه از طرف كف آسانسور بر اجسام داخل آسانسور وارد می شود همان وزن ظاهری جسم داخل آسانسور با محتوياتش است .
جسمی به جرم \(3Kg\) را به انتهای فنری با ثابت \(50\frac{N}{{cm}}\) بسته ایم و فنر را از سقف یک آسانسور آویزان می کنیم. اگر آسانسور با شتاب ثابت به طرف بالا شروع به حرکت کند و تغییر طول فنر \(0/72cm\) باشد، اندازه شتاب آسانسور چقدر است؟ (\(g = 10\frac{m}{{{s^2}}}\) )
\(\begin{array}{l}{F_e} - mg = ma \to kx = m(g + a) \to 50 \times 0/72 = 30 + 3a\\36 - 30 = 3a \to a = 2\frac{m}{{{s^2}}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تکانه
تکانه
حاصل ضرب جرم جسم در سرعتش تكانه ناميده می شود.
بردار تکانه (\(\vec P = m\vec V\) )
اندازه ی تکانه (\(P = mV\) )
تكانه كميتی برداری است و بردار آن هم جهت با بردار سرعت جسم است.
تغييرات تكانه، به صورت زير به دست می آيد:
بردار تغییرات تکانه (\(\Delta \vec P = m\Delta \vec V\) )
اندازه ی تغییرات تکانه (\(\Delta P = m\Delta V\) )
رابطه ی تكانه و قانون دوم نيوتن (رابطه ی نيرو و تغييرات تكانه)
بردار نیروی خالص
\({\vec F_{av}} = \frac{{\Delta \vec P}}{{\Delta t}}\)
اندازه ی بردار نیروی خالص
\({F_{av}} = \frac{{\Delta P}}{{\Delta t}}\)
1 شيب خط واصل بين دو نقطه در نمودار P-t نيروی متوسط وارد بر جسم است.
2 شيب خط مماس بر نمودار P-t در هر لحظه ، نيروی وارد بر جسم در آن لحظه است.
3 مساحت زير نمودار F-t برابر تغييرات تكانه ی جسم (\(\Delta P\)) است.
انرژی جنبشی با تكانه رابطه ای به صورت زير است:
\(K = \frac{{{P^2}}}{{2m}}\)
تکانه (\(\frac{{Kg \times m}}{s}\) )
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
نیروی گرانشی
نیروی گرانشی
نيروی جاذبه بين دو جسم دارای جرم نيروی گرانشی ناميده می شود. (طبق قانون سوم نيوتن اين دو يک جفت نيروی كنش-واكنش را تشكيل می دهند)
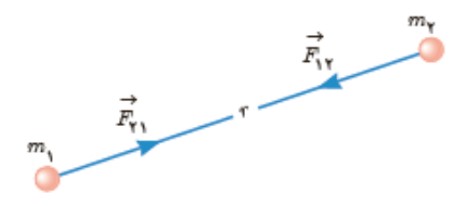
تعريف قانون عمومی گرانش
نيروی گرانش ميان دو ذره با حاصل ضرب جرم دو ذره نسبت مستقيم و با مربع فاصله ی آن ها از يكديگر نسبت وارون دارد:
\(F = \frac{{G{m_1}{m_2}}}{{{r^2}}},G = 6/67 \times {10^{ - 11}}\frac{{N \times {m^2}}}{{K{g^2}}}\)
جزئيات بيش تر در رابطه با نيروی وزن
با توجه به اينكه نيروی وزن نوعی نيروی گرانش محسوب می شود، بايد با حالت های زير برای نيروی وزن آشنا باشيد:
1) نيروی وزن در سطح زمين
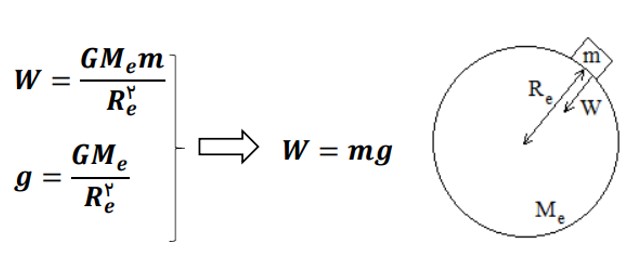
\({M_e}\) جرم کره زمین
\({{\mathop{\rm R}\nolimits} _e}\) شعاع کره زمین
\(g\) شتاب گرانش در سطح زمین
2) نيروی وزن در ارتفاع معينی از سطح زمين
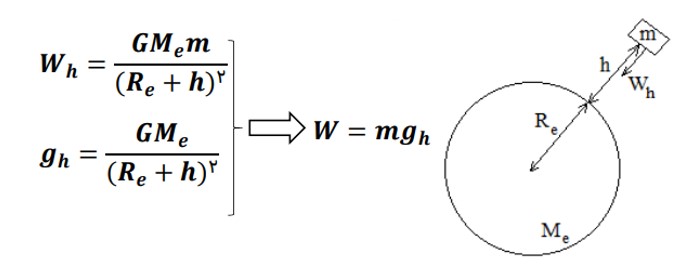
\({M_e}\) جرم کره زمین
\({{\mathop{\rm R}\nolimits} _e}\) شعاع کره زمین
H ارتفاع از سطح زمین
\({g_h}\) شتاب گرانش در سطح زمین
3) نیروی وزن در کرات و سیارات دیگر
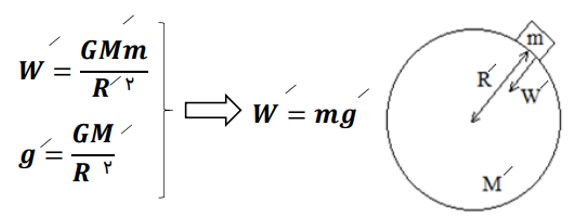
\(M'\) جرم سیاره
\(R'\) شعاع سیاره
\(g'\) شتاب گرانش در سطح سیاره
سیاره ای به شعاع \({10^4}\) کیلومتر و جرم \(2 \times {10^{25}}\) به دور خود می چرخد. شتاب گرانشی در سطح این سیاره چند \(\frac{m}{{{s^2}}}\) است؟ (\(G = 6/7 \times {10^{ - 11}}\frac{{N{m^2}}}{{K{g^2}}}\) )
\(g = \frac{{GM}}{{{r^2}}} \to g = \frac{{6/7 \times {{10}^{ - 11}} \times 2 \times {{10}^{25}}}}{{{{({{10}^7})}^2}}} \to g = 13/4\frac{m}{{{s^2}}}\)
حرکت دایره ای یکنواخت
حرکت دایره ای یکنواخت
حركت جسمی روی يک دايره يا بخشی از آن كه با تندی ثابت انجام می شود حركت دايره ای يكنواخت نام دارد.
همان طور كه قبل تر گفته شد در هر مسيری بردار سرعت مماس بر مسير است.
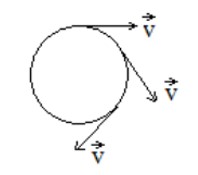
در حركت دايره ای يكنواخت اندازه سرعت ( تندی) ثابت است اما جهت بردار سرعت تغيير می كند، بنابراين يک حركت شتاب دار محسوب می شود.
در حركت دايره ای يكنواخت ذره در بازه های زمانی برابر، مسافت های يكسانی را طی می كند. (زيرا در زمان های مساوی زاويه ها ی يكسانی را می چرخد)
دوره تناوب در حركت دايره ای يكنواخت
زمان لازم برای پيمودن يک دور محيط دايره را دوره ی تناوب (دوره) می نامند، كه با فرمول های زير محاسبه می گردد:
\(\begin{array}{l}T = \frac{{2\pi r}}{V}\\T = \frac{t}{N}\end{array}\)
r)) شعاع دايره
V)) اندازه ی سرعت
t)) زمان كل گردش ها
N)) تعداد كل گردش ها
T)) دوره يا زمان تناوب
بسامد در حركت دايره ای يكنواخت
تعداد گردش ها در هر ثانيه است كه به صورت زير محاسبه می گردد:
\(f = \frac{N}{t}\)
محاسبه ی زاويه ای كه ذره در يک بازه ی زمانی روی دايره می چرخد:
اين زاويه برحسب راديان به صورت زير به دست می آيد:
\(\Delta \theta = \frac{{2\pi }}{T}\Delta t\)
شتاب مركز گرا در حركت دايره ای يكنواخت
همانطور كه گفته شد در حركت دايره ای يكنواخت، اندازه ی سرعت ثابت است اما جهت آن دائم تغيير می كند به همين دليل اين حركت يک حركت شتاب دار است، شتاب حركت همواره به سمت مركز دايره است و اندازه ی آن به صورت زير محاسبه می شود:
\(\begin{array}{l}{a_c} = \frac{{{V^2}}}{r}\\{a_c} = \frac{{4{\pi ^2}r}}{{{T^2}}}\end{array}\)
قانون دوم نيوتن در حركت دايره ای يكنواخت
از آنجا كه شتاب يک جسم را نيروی خالص وارد بر آن ايجاد می كند و شتاب جسم همواره در راستا و جهت نيروی خالص وارد بر جسم است، بنابراين در اين حركت همواره يک نيروی خالص رو به مركز دايره وجود دارد كه به آن نيروی مركز گرا گفته می شود:
\(\begin{array}{l}{F_{net}} = m{a_c} \to {F_{net}} = \frac{{m{V^2}}}{r}\\{F_{net}} = m{a_c} \to {F_{net}} = \frac{{4{\pi ^2}rm}}{{{T^2}}}\end{array}\)
در رابطه ی فوق به جاي \({F_{net}}\) می توان برآیند نیرو های وارد بر جسم در راستای شعاع دایره را نوشت. )در واقع نيروی مركز گرا نوع جديدی از نيرو نيست و نيروهايی مانند كشش ريسمان، نيروی فنر، اصطكاک و . . . می توانند همان نيروی مركزگرا باشند.)
حرکت ماهواره ای
حركت ماهواره ها و كره ی ماه به دور كره ی زمين را حركت ماهواره ای می گويند، تنها نيرويی كه بر چنين اجرامی وارد می شود نيروی گرانش است (\({F_r} = {W_h}\) )، بنابراين شتاب مركز گرا نيز همان شتاب گرانش است و برای حركت های ماهواره ای روابطی به صورت زير می توان نوشت:
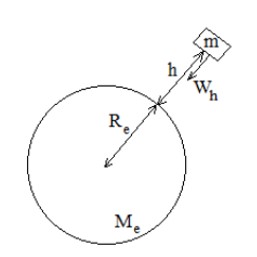
\(\begin{array}{l}{a_c} = {g_h} \to \frac{{{V^2}}}{r} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\\{a_c} = {g_h} \to \frac{{4{\pi ^2}r}}{{{T^2}}} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\\ \to r = {{\mathop{\rm R}\nolimits} _e} + h\end{array}\)
1 با توجه به روابط فوق، برای سرعت حركت ماهواره رابطه ای به صورت زير می توان اثبات نمود:
\(V = \sqrt {\frac{{G{M_e}}}{{{{\mathop{\rm R}\nolimits} _e} + h}}} \)
2 با توجه به روابط فوق، برای دوره تناوب حركت ماهواره ای رابطه ای به صورت زير می توان اثبات نمود:
\(T = 2\pi \sqrt {\frac{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^3}}}{{G{M_e}}}} \)
ماهواره ای با تندی \(6 \times {10^3}\frac{m}{s}\) روی یک مدار تقریباً دایره ای به دور زمین می چرخد. اگر جرم ماهواره \(200Kg\) و فاصله آن از مرکز زمین \(9000Km\) باشد، نیروی گرانشی ای که زمین بر ماهواره وارد می کند را حساب کنید.
\(F = \frac{{m{V^2}}}{r} \to F = \frac{{200 \times {{(6 \times {{10}^3})}^2}}}{{9 \times {{10}^6}}} = 800N\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی



1736019749.png)















