درسنامه کامل فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دوازدهم ریاضی فصل 3 نوسان و موج - درسنامه شب امتحان فیزیک دوازدهم ریاضی فصل 3 نوسان و موج - جزوه شب امتحان فیزیک دوازدهم ریاضی نوبت اول فصل 3 نوسان و موج
چرخه
چرخه
تكرار منظم يک حركت چرخه يا سيكل نوسان گفته می شود.
انواع نوسان ها
نوسان ها به دو دسته ی زير تقسيم می شوند:
1) نوسان دوره ای
نوسان هايی كه را كه هر چرخه ی آن در دورهای ديگر تكرار می شود نوسان دوره ای می نامند. مانند (مانند ضرب آهنگ (ریتم)، قلب انسان)
2) نوسان غیر دوره ای
نوسان روی خط راست
يک رفت و برگشت نوسانگر، نوسان ناميده می شود. هر نوسان دارای 4 قسمت به شكل زير است:
دوره تناوب
مدت زمان يک نوسان (چرخه)، دوره تناوب حركت ناميده می شود، كه به صورت زير محاسبه می گردد:
\(T = \frac{t}{N}\)
بسامد(فركانس)
تعداد نوسان های انجام شده (تعداد چرخه) در هر ثانيه بسامد ناميده می شود كه به صورت زير محاسبه می گردد:
\(f = \frac{N}{t}\)
دوره تناوب و بسامد رابطه ای به صورت زير دارند:
\(f = \frac{1}{T}\) یا \(T = \frac{1}{f}\)
حركت هماهنگ ساده (SHM)
به نوسان های سينوسی، حركت هماهنگ ساده گفته می شود.
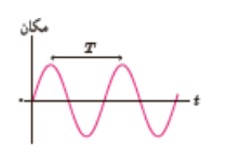
حركت هماهنگ ساده، مبنايی برای درک هر نوع نوسان دوره ای ديگر است زيرا در سطوح بالاتر نشان داده می شود كه هر نوسان دوره ای را می توان مجموعی از نوسان های سينوسی در نظر گرفت.
حركت نوسانی وزنه-فنر
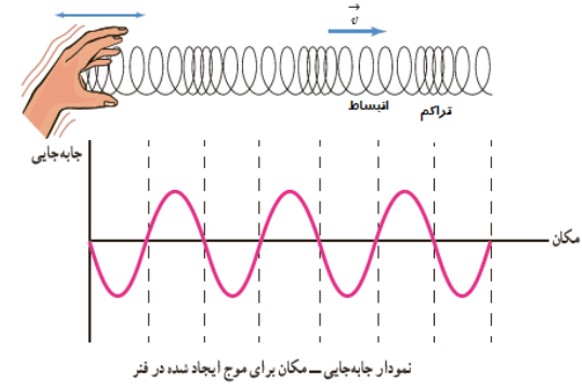
يک نمونه معروف از حركت هماهنگ ساده است. اگر فرض كنيم نوسان روی سطح بدون اصطكاكی صورت می گيرد و مكان جسم را در بازه های متوالی و يكسان ثبت كنيم به نموداری سينوسی می رسيم كه در شكل مقابل آمده است:
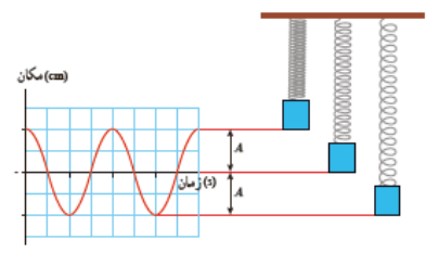
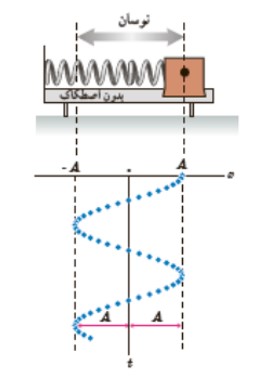
نقطه تعادل (مرکز نوسان)
وسط پاره خط نوسانی مركز نوسان گفته می شود.
دامنه نوسان (A)
بيشترين فاصله ی نوسانگر از نقطه ی تعادل دامنه ناميده می شود.

نقاط بازگشت حركت
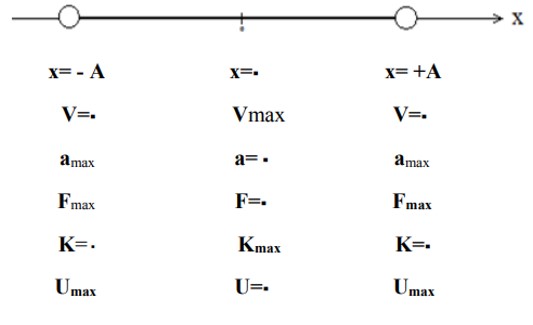
وقتی نوسانگر در مكان \(x = \pm A\) است، سرعت آن برابر صفر است. به اين نقطه ها نقاط بازگشت حركت می گوييم.
بسامد زاويه ای
رابطه ای به صورت زير دارد:
\(\omega = \frac{{2\pi }}{T}\)
بسامد زاویه (\(\frac{{rad}}{s}\) )
ويژگی های كلی حركت نوسانی
انرژی مكانيكی (E) در كل حركت نوسانی ثابت است.
علامت و جهت سرعت، شتاب و نيرو در حركت نوسانی
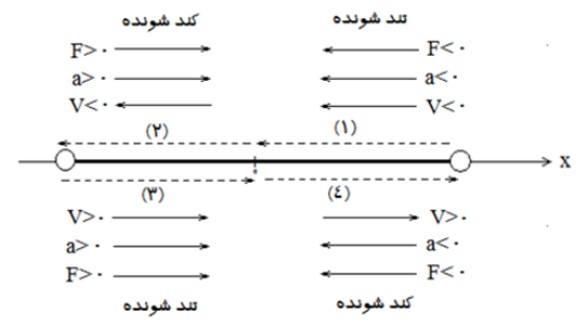
1) سرعت (V) همواره در جهت حركت است.
2) شتاب (a) و نیرو (F) همواره به سمت مركز نوسان است.
علامت هر يک از بردارهای فوق كه در جهت محور x باشد، مثبت، و هركدام كه در خلاف جهت محور x، باشد منفی است.
معادله و نمودار مكان-زمان در حركت نوسانی
\(X = A\cos \omega t\)
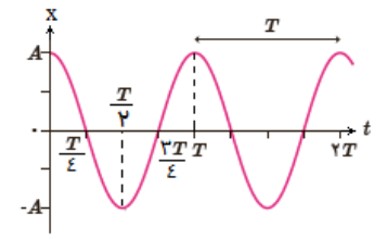
X مکان نوسانگر
A دامنه
\(\omega \) بسامد زاویه ای (\(rad.{s^{ - 1}}\) )
T دوره
بيشينه سرعت نوسانگر
نوسانگر هماهنگ ساده هنگامی كه به نقطه ی تعادل می رسد سرعتش بيشينه می شود كه اين بيشينه ی سرعت با را بطه ی زير قابل محاسبه است:
\({V_m} = A\omega \)
معادله شتاب-مكان در حركت نوسانی
\(a = - {\omega ^2}x\)
با توجه به اينكه يک نوسان كامل 4 قسمت دارد و اين 4 قسمت به اندازه يک دوره (T) زمان نياز دارد، می توان نتيجه گرفت هر يک از 4 قسمت \(\frac{T}{4}\) زمان نیاز دارد:
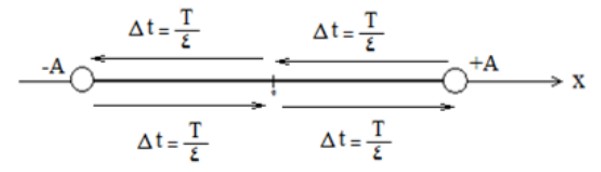
دوره تناوب نوسانگر جرم-فنر
علاوه بر فرمول های قبلی رابطه ی زير برای محاسبه ی دوره تناوب سامانه وزنه-فنر قابل محاسبه است:
\(\begin{array}{l}T = 2\pi \sqrt {\frac{m}{k}} \\k = m{\omega ^2}\end{array}\)
با توجه به رابطه فوق می توان گفت دوره و بسامد نوسانگر وزنه-فنر به دو عامل جرم و ثابت فنر بستگی دارد.
دامنه نوسان یک حرکت هماهنگ ساده \(4cm\) و بسامد آن \(40Hz\) است. معادله حرکت این نوسانگر را بنویسید.
\(\begin{array}{l}\omega = 2\pi f \to \omega = 2\pi \times 40 = 80\pi \frac{{rad}}{s}\\x = A\cos \omega t \to {x_{(cm)}} = 4\cos 80\omega t\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
آونگ
آونگ
آونگ ساده شامل وزنه ی كوچكی به جرم m است كه از نخی بدون جرم و كش نيامدنی به طول L كه سر ديگر آن ثابت شده، آويزان است. اگر زاويه ی انحراف آونگ از وضع تعادل كوچک باشد، آونگ حركت هماهنگ ساده خواهد داشت و علاوه بر تمام روابط حركت هماهنگ ساده، رابطه ی زير نيز برای دوره تناوب آن بر قرار است:
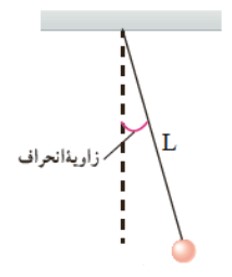
\(T = 2\pi \sqrt {\frac{L}{g}} \)
1 دوره تناوب و بسامد آونگ تنها به طول آن و شتاب گرانش محل نوسان آونگ بستگی دارد (دوره و بسامد آن به جرم وزنه ی متصل به آن بستگی ندارد)
2 وابسته بودن دوره ی آونگ به شتاب گرانش باعث می شود كه با اندازه گيری طول (L) و دوره ی آن (T) بتوان به طور دقيق شتاب گرانش يک محل را به دست آورد.
3 شتاب گرانش در سطح زمين، ارتفاعات زمين و ساير كرات ديگر روابطی در ديناميک دارد كه آنها را برايتان يادآوری می كنيم:
شتاب گرانش در سطح زمین : \(g = \frac{{G{M_e}}}{{R_e^2}}\)
شتاب گرانش در ارتفاعات زمین : \({g_h} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\)
شتاب گرانش در کرات و سیارات دیگر : \(g' = \frac{{GM'}}{{{{R'}^2}}}\)
دوره آونگ ساده ای 2 ثانیه است. طول این آونگ چند متر است؟ (\({\pi ^2} = g\) )
\(T = 2\pi \sqrt {\frac{L}{g}} \to 2 = 2\pi \sqrt {\frac{L}{g}} \to 1 = {\pi ^2}(\frac{L}{{10}}) \to L = 1m\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
انرژی در حرکت هماهنگ ساده
انرژی در حرکت هماهنگ ساده
انرژی جنبشی در حركت هماهنگ ساده
با توجه به فيزيک 1 به صورت زير قابل محاسبه است:
\(K = \frac{1}{2}m{V^2}\)
انرژي پتاسيل در حركت هماهنگ ساده
برای اين انرژی رابطه ای در كتاب درسی نيامده است ولی با كمک انرژی جنبشی (K) و انرژی مكانيكی (E) می توان آن را به دست آورد.
انرژی مكانيكی در حركت هماهنگ ساده
انرژی مكانيكی، مجموع انرژی جنبشی و انرژی پتانسيل است و به صورت زير می توان برای آن رابطه نوشت:
\(\begin{array}{l}E = U + K\\E = \frac{1}{2}m{\omega ^2}{A^2}\end{array}\)
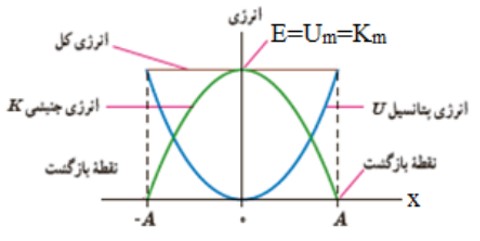
1 چون در حركت هماهنگ ساده از اصطكاک صرف نظر می شود انرژی مكانيكی ثابت می ماند، به عبارت ديگر برای يک نوسانگر، مجموع انرژی جنبشی و پتانسيل در تمام نقاط حركت برابر است و اين يعنی در طول حركت هر مقدار انرژی جنبشی كاهش يابد بر انرژی پتانسيل افزوده می شود و برعكس.
2 هنگامی كه انرژی پتانسيل بيشينه است، انرژی جنبشی صفر است و هنگامی كه انرژی پتانسيل صفر است انرژی جنبشی بيشينه است و اين يعنی بيشينه ی انرژی جنبشی و بيشينه ی انرژی پتانسيل برابر انرژی مكانيكی است، پس:
\({K_m} = {U_m} = \frac{1}{2}m{\omega ^2}{A^2}\)
نمودار انرژی جنبشی و انرژی پتانسيل بر حسب مكان:
نوسان
نوسان
بسامد طبيعی
هر نوسانگر با انحراف از وضع تعادل با بسامدی معين شروع به نوسان می كند. به اين نوسان ها بسامد طبيعی گفته می شود. (بسامد اين نوسان با \({f_o}\) نمايش داده می شود.)
نوسان واداشته
هر نوسانگری با اعمال نيروی خارجی با بسامد متفاوتی نسبت به بسامد طبيعی شروع به نوسان می كند، به چنين نوسانی، نوسان واداشته گفته می شود. (بسامد اين نوسان با \({f_d}\) نمايش داده می شود.)
نوسان ميرا
اتلاف انرژی و اصطكاک برای هر نوسانگری كه با بسامد طبيعی نوسان می كند سبب می شود كه پس از مدتی نوسان متوقف گردد، به چنين نوسانی ، نوسان ميرا گفته می شود.
1 تاب خوردن يک كودک بدون هل دادن يک نوسان طبيعی است، اگر هل داده شود يک نوسان واداشته است، و اين هل دادن باعث جبران اتلاف انرژی و مقاومت هوا می گردد و مانع از ميرا شدن نوسان تاب می گردد.
2 با توجه به روابط آونگ ساده و نوسان وزنه-فنر می توان گفت بسامد طبيعی آونگ ساده به صورت \({f_o} = \frac{1}{{2\pi }}\sqrt {\frac{g}{L}} \) و بسامد طبیعی وزنه-فنر به صورت \({f_o} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) است.
تشديد يا رزونانس
اگر به يک نوسانگر به صورت دوره ای نيرو وارد كنيم و بسامد اين نيرو با بسامد طبيعی نوسانگر برابر باشد (\({f_d} = {f_o}\) ) باشد، دامنه ی نوسانگر تا مقدار معينی بزرگ شده و سپس با همين دامنه نوسان خود را ادامه می دهد، به اين پديده تشديد گفته می شود.
اگر بسامد نيروی وارد بر نوسانگر، بيش تر يا كم تر از نوسان طبيعی آن باشد تشديد رخ نمی دهد ودامنه ی نوسان كوچكتر از حالتی خواهد شد كه بسامد نيرو با بسامد طبيعی برابر است.
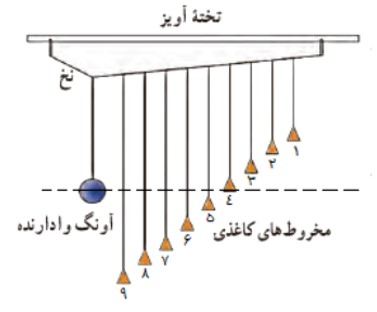
آونگ های بارتون
یک آونگ با وزنه ی سنگين و تعدادی آونگ سبک با طول های متفاوت را مطابق شكل زیر در نظر بگيريد. آونگ ها روی نخی سوار شده اند كه هر دو انتهای آن توسط گيره هايی به تخته آويز متصل شده است. به آونگ سنگين اصطلاحا آونگ وادارنده گفته می شود، زيرا به نوسان در آوردن اين آونگ، موجب تاب خوردن نخ آويز و در نتيجه به نوسان واداشتن ساير آونگ ها می شود. اما از آنجا كه بسامد آونگ مطابق رابطه ی \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{L}} \) با جذر طول (\(\sqrt L \) ) رابطه مستقيم دارد، بسامد آونگ وادارنده و بسامد آونگ شماره 4 يكسان است (\({f_d} = {f_o}\) ) و در آونگ 4 تشديد رخ می دهد، يعنی دامنه ی نوسان آن بيش از ساير آونگ ها می شود و به مدت طولانی تری نوسان می كند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
موج
موج
هرگاه در ناحيه ای از محيط كشسان ارتعاشی به وجود آيد، موجب پديد آمدن ارتعاش های پی در پی ديگری می شود كه از محل شروع ارتعاش دور و دور ترند و به اين ترتيب موج حاصل می شود.
انواع موج با توجه به محيط انتشار:
1) موج مكانيكی
امواجی كه برای انتشار خود نياز به محيط مادی كشسان دارند موج مكانيكی هستند. ( مانند امواج روی سطح آب و امواج صوتی)
2) موج الكترومغناطيسی
امواجی كه برای انتشار خود نياز به محيط مادی ندارند موج الكترومغناطيسی هستند. (مانند نور مرئی، موج های راديويی و تلويزيونی، ميكروموج ها و پرتوهای X)
تپ موج
تغيير يا آشفتگی ايجاد شده در يک محيط كشسان را تپ موج می گوييم.
موج پيشرونده
موجی است كه از نقطه ای به نقطه ی ديگر حركت كرده و انرژی را با خود منتقل می كنند. (در اين امواج ماده منتقل نمی شود)
انواع موج پيش رونده
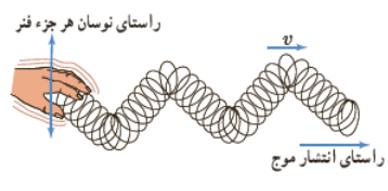
1) موج عرضی
موجی است كه راستای جابه جايی هر جزء نوسان كننده (راستای ارتعاش) عمود بر راستای حركت موج (راستای انتشار) است. تصوير زير موج عرضی روی فنر را نشان می دهد.
2) موج طولی
موجی است كه راستای جابه جايی هر جزء نوسان كننده (راستای ارتعاش) منطبق بر راستای حركت موج( راستای انتشار) است. تصوير زير موج طولی روی فنر را نشان می دهد.
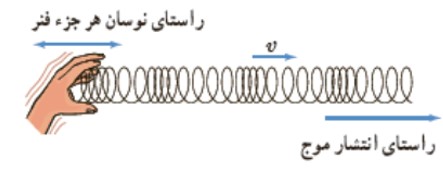
چشمه موج
چشمه موج معمولاً يک نوسانگر است كه حركت هماهنگ ساده انجام می دهد و بسامد يک موج همان بسامد چشمه ی موج است.
جبهه موج روی سطح آب
برآمدگی ها يا فرورفتگی های ايجاد شده روی سطح آب، يی جبهه موج ناميده می شود. (به برآمدگی ها قله يا ستيغ و به فرو رفتگی ها دره يا پاستيغ گفته می شود)
دامنه ی موج (A)
بيشينه ی فاصله ی يک ذره از مكان تعادل، دامنه ی موج ناميده می شود. (همان فاصله ی قله يا دره نسبت به سطح آرام يا ساكن است)
دوره تناوب موج (T)
مدت زمانی كه هر ذره ی محيط يک نوسان كامل انجام می دهد دوره تناوب موج ناميده می شود.
بسامد موج (f)
تعداد نوسان های انجام شده توسط هر ذره از محيط در يک ثانيه بسامد موج ناميده می شود.
تندی انتشار موج (V)
مسافت طی شده توسط موج در واحد زمان تندی انتشار ناميده می شود:
\(V = \frac{L}{{\Delta t}}\)
1 بسامد و دوره تناوب موج همان بسامد ودوره ی چشمه ی موج است و به ويژگی های فيزيكی چشمه ی موج بستگی دارند و به ويژگی های محيط انتشار وابسته نيستند.
2 تندی انتشار موج به جنس و ويژگی های محيط انتشار بستگی دارد و به ويژگی های چشمه ی موج وابسته نيست.
3 با افزايش عمق آب، تندی انتشار امواج روی سطح آب نيز بيش تر می شود.
4 اختلاف زمانی دو موج با تندی متفاوت به صورت زير قابل محاسبه است:
\(\Delta {t_T} = \Delta {t_2} - \Delta {t_1} \to \Delta {t_T} = \frac{L}{{{V_2}}} - \frac{L}{{{V_1}}}\)
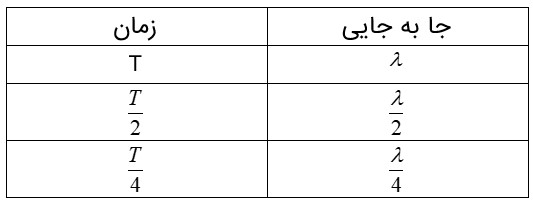
طول موج (\(\lambda \))
مسافتی است كه موج در مدت دوره تناوب نوسان چشمه طی می كند.
\(\begin{array}{l}\lambda = \frac{V}{f}\\\lambda = VT\end{array}\)
با توجه به مفهوم طول موج می توان گفت در مدت زمان) Tدوره) مسافتی كه موج می پيمايد برابر \(\lambda \) است، همچنين برای مسافتی كه موج می پيمايد و زمان، می توان تناسب هايی به صورت زير نوشت:
مشخصه های موج عرضی
فاصله ی دو قله ی متوالی يا دو دره ی متوالی در امواج عرضی برابر طول موج است، همچنين بيشينه ی فاصله ی هر نقطه از مركز نوسان دامنه است:
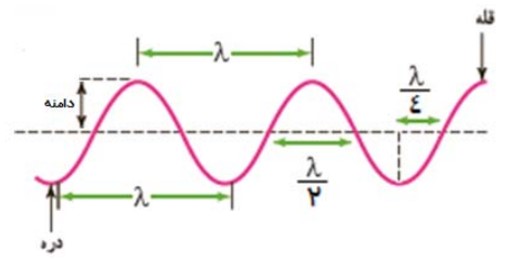
برای تعيين جهت حركت هر ذره روی موج عرضی به وضعيت نقاط قبل تر از آن توجه كنيد. جهت حركت هر نقطه به سمت نقاط قبل تر از خودش است.
مشخصه های موج طولی
فاصله دو انبساط (بازشدگی) متوالی يا دو تراكم (جمع شدگی) متوالی در امواج طوليی برابر طول موج است، همچنين بيشينه ی فاصله ی هر نقطه از مركز نوسان، دامنه است:
برای امواج مكانيكی، تندی انتشار امواج طولی در يک محيط جامد بيش تر از تندی انتشار امواج عرضی در همان محيط است.
امواج لرزه ای
امواج لرزه ای، موج های مكانيكی هستند كه از لايه های زمين عبور می كنند. يكی از منشأ های مهم امواج لرزه ای، زمين لرزه ها هستند. انواع امواج لرزه ای عبارتند از:
- امواج P يا امواج اوليه كه طولی بوده و سرعت بيش تری داشته و سريع تر به دستگاه لرزه نگار می رسد.
- امواج S يا امواج ثانويه كه عرضی بوده و سرعت كم تری داشته و دير تر به دستگاه لرزه نگار می رسد.
انتقال انرژی در موج عرضی
هر موجی حامل انرژی است. می توان ثابت كرد كه متوسط آهنگ انتقال انرژی (توان متوسط) در يک موج عرضی برای همه ی امواج مكانيكی با دو عامل زير متناسب است:
1) مربع دامنه (\({A^2}\) )
2) مربع بسامد (\({f^2}\) )
محاسبه تندی انتشار موج عرضی در تار (سيم) يا فنر:
\(V = \sqrt {\frac{F}{\mu }} = \sqrt {\frac{{FL}}{m}} = \sqrt {\frac{F}{{\rho A}}} = \frac{1}{r}\sqrt {\frac{F}{{\rho \pi }}} = \frac{2}{D}\sqrt {\frac{F}{{\rho \pi }}} \)
\(\mu \) چگالی خطی (\(Kg.{m^{ - 1}}\) )
M جرم تار
L طول تار
A سطح مقطع تار
R شعاع مقطع تار
D قطر مقطع تار
\(\rho \) چگالی
V تندی انتشار در تار
\(\begin{array}{l}\mu = \frac{m}{L}\\\rho = \frac{m}{V} \to m = \rho V\\V = AL = \pi {r^2}L\end{array}\)
1شکل مقابل نشان دهنده انتشار کدام موج در طول فنر است؟ چرا؟
موج عرضی زیرا، جابجایی هر جزء نوسان کننده از فنر، در راستای عمود بر حرکت موج است.
2یک موج مکانیکی از محیط 1 وارد محیط 2 می شود و تندی انتشار آن افزایش می یابد. طول موج و بسامد موج چگونه تغییر می کنند؟
طول موج افزایش می یابد و بسامد ثابت می ماند.
بسامد از ویژگی های چشمه موج است لذا از محیطی به محیط دیگر، ثابت می ماند ولی طبق رابطه \(V = f\lambda \) ، سرعت و طول موج رابطه مستقیم دارند؛ لذا اگر سرعت افزایش یابد طول موج نیز افزایش می یابد.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دوازدهم ریاضی فصل 1 حرکت بر خط راست
جزوه جامع فیزیک دوازدهم ریاضی فصل 2 دینامیک و حرکت دایره ای
جزوه جامع فیزیک دوازدهم ریاضی فصل 3 نوسان و موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 4 برهم کنش های موج
جزوه جامع فیزیک دوازدهم ریاضی فصل 5 آشنایی با فیزیک اتمی
جزوه جامع فیزیک دوازدهم ریاضی فصل 6 آشنایی با فیزیک هسته ای
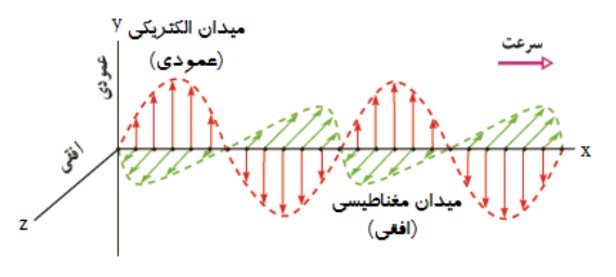
موج الکترومغناطیسی
موج الکترومغناطیسی
- بار الكتريكی ، ميدان الكتريكی ايجاد می كند.
- جريان الكتريكی، ميدان مغناطيسی توليد می كند.
- اگر بارهای الكتريكی ساكن باشند، ميدان الكتريكی حاصل از آن ها با زمان تغيير نمی كند.
- اگر جريان الكتريكی ثابت باشد، ميدان مغناطيسی حاصل از آن ثابت و بدون تغيير می شود.
نحوه ايجاد موج الكترومغناطيس
امواج الكترومغناطيسی از رابطه ی متقابل ميدان های الكتريكی و مغناطيسی به وجود می آيند. يعنی هر تغييری در ميدان الكتريكی در هر نقطه از فضا، ميدان مغناطيسی متغيری ايجاد می كند و اين ميدان مغناطيسی متغير، خود ميدان الكتريكی متغيری به وجود می آورد. اين رابطه ی متقابل ميدان ها سبب انتقال نوسان ها ی ميدان های الكتريكی و مغناطيسی از يک نقطه ی فضا به نقاط ديگر و يا همان انتشار موج الكترومغناطيسی می شود.
ايجاد ميدان الكتريكی به علت تغيير ميدان مغناطيسی همان قانون القای الكترومغناطيس است كه توسط مايكل فاراده كشف شد.
نظر ماكسول در مورد موج الكترومغناطيس
عكس قانون فاراده توسط جيمز كلارک ماكسول پيش بيني شد، يعنی او پيش بينی كرد كه همانطور كه طبق قانون فاراده بر اثر تغيير ميدان مغناطيسی می توان ميدان الكتريكی توليد نمود، بر اثر تغيير ميدان الكتريكی نيز می توان ميدان مغناطيسی توليد نمود. ماكسول از اين دو پديده نتيجه گرفت كه امواج الكترومغناطيس بايد لزوماً ناشی از تغييرات هم زمان ميدان های الكتريكی و مغناطيسی (اصطلاحاً ميدان الكترومغناطيسی) باشد.
تصويری از يک موج الكترومغناطيس و نحوه ی انتشار آن:
مهمترين مشخصات موج الكترومغناطيسی
- ميدان الكتريكی (E) همواره عمود بر ميدان مغناطيسی (B) است.
- ميدان الكتریکی و مغناطيس (E) و (B) همواره بر جهت حركت موج عمودند و در نتيجه موج الكترومغناطيسی، يک موج عرضی است.
- ميدان های الكتريكی و مغناطيسی با بسامد يكسان و همگام با يكديگر تغيير می كنند.
نحوه تعيين جهت انتشار موج الكترومغناطيسی
با كمک قاعده ی دست راست تعيين می شود.
تندی انتشار امواج الكترومغناطيس
ماكسول با يک تحليل رياضی نشان داد كه تندی انتشار امواج الكترومغناطيس در هوا يا خلأ از رابطه ی زير به دست می آيد:
\(C = \frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }} = 3 \times {10^8}\)
\({\mu _0}\) تراوایی مغناطیسی خلاء (\(4\pi \times {10^{ - 7}}\frac{{T.m}}{A}\) )
\({\varepsilon _0}\) تراوايی الكتريكي خلاء (\(8/85 \times {10^{ - 12}}\frac{{{C^2}}}{{N.{m^2}}}\) )
C تندی انتشار موج الكترومغناطيس در هوا يا خلاء (\(\frac{m}{s}\) )
انرژی امواج الكترو مغناطيس
انرژی اين امواج مانند امواج مكانيكی به صورت انرژی جنبشی و پتانسيل ذرات محيط نيست (زيرا اين امواج برای انتشار نياز به محيط مادی ندارند) بلكه اين امواج انرژی را به صورت انرژی ميدان های الكتريكی و مغناطيسی منتقل می كنند.
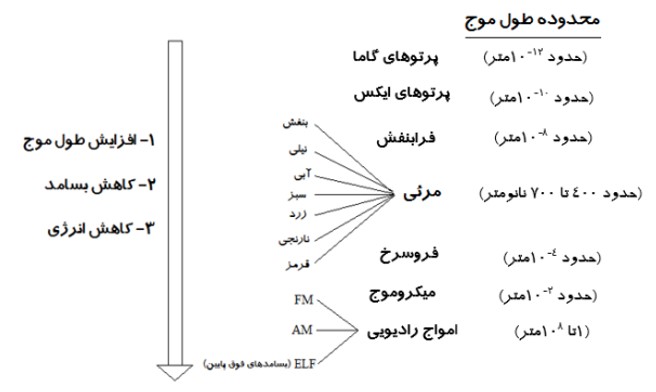
طيف امواج الكترومغناطيسی
اين طيف به ترتيب افزايش طول موج به صورت زير است. (هيچ گسستگی در اين طيف وجود ندارد و همگی با تندی نور درخلأ حركت می كنند)
امواج الکترومغناطیسی طولی هستند یا عرضی؟ چرا؟
عرضی ،چون راستای نوسان میدان های الکتریکی و مغناطیسی بر راستای انتشار موج عمود است.
موج صوتی
موج صوتی
صوت يک موج مكانيكی طولی است كه توسط جسم مرتعش توليد می شود. (به اين جسم مرتعش نيز چشمه ی صوت گفته می شود)
1 انتشار صوت با تندی ثابت و در تمام جهات به صورت سه بعدی صورت می گيرد. (جبهه های موج كروی است)
2 هنگام انتشار صوت هر مولكول هوا، با موج حركت نمی كند، بلكه در مكان ثابتی نوسان می نمايد.
3 هر چه محيطی متراكم تر باشد سرعت انتشار آن نيز بيش تر می شود، به طور مثال سرعت انتشار در جامدها بيش تر از مايعات و در مايعات نيز بيش تر از گازها است. (البته استثناهايی نيز وجود دارد)
4 چشمه ی صوت برای انتقال انرژی، لايه ای از محيط كه در تماس با آن است را به حركت در می آورد و انرژی از اين لايه به لايه ی بعدی در تمام جهات منتشر می شود.
5 با توجه به اينكه صوت حركت يكنواخت انجام می دهد رابطه ی زير برای آن برقرار است:
\(V = \frac{L}{{\Delta t}}\)
عوامل مؤثر بر تندی صوت
- جنس محيط انتشار
- دمای محيط انتشار
شدت صوت (I)
شدت صوت برابر با آهنگ متوسط انرژی ای است كه توسط موج به واحد سطح، عمود بر راستای انتشار صوت می رسد.
\(\begin{array}{l}I = \frac{P}{A}\\I = \frac{P}{{4\pi {r^2}}}\end{array}\)
P متوسط توان چشمه صوتی (W)
I شدت صوت (\(\frac{W}{{{m^2}}}\) )
R فاصله از چشمه صوت (m)
A مساحت جبه های موج صوتی (\({m^2}\) )
عوامل مؤثر بر شدت صوت
1) مجذور دامنه (\({A^2}\) )
2) مجذور بسامد (\({f^2}\) )
3) مجذور فاصله (\({r^2}\))
براساس 3 عامل فوق رابطه ای به صورت زير می توان برای مقايسه ی دو شدت صوت نوشت:
\(\frac{{{I_2}}}{{{I_1}}} = {(\frac{{{A_2}}}{{{A_1}}} \times \frac{{{f_2}}}{{{f_1}}} \times \frac{{{r_1}}}{{{r_2}}})^2}\)
تراز شدت صوت يا تراز صوتی (\(\beta \))
به صورت زير و برای تشخيص مقدار بلندی صوت محاسبه می شود:
(b) بر حسب بل : \(\beta = Lo{g^{\frac{I}{{{I_o}}}}}\)
(db) بر حسب دسی بل : \(\beta = 10Lo{g^{\frac{I}{{{I_o}}}}}\)
\({I_o}\) شدت صوت مرجع يا حد پايين شنوای انسان (\({10^{12}}\frac{W}{{{m^2}}}\) )
I شدت صوت (\(\frac{W}{{{m^2}}}\) )
\(\beta \) تراز شدت صوت
مقايسه دو تراز شدت صوت
هر گاه دو تراز صوتی در سؤالی مطرح شد، به صورت زير رابطه بنويسيد:
بر حسب بل : \({\beta _2} - {\beta _1} = Lo{g^{\frac{{{I_2}}}{{{I_1}}}}}\)
بر حسب دسی بل : \({\beta _2} - {\beta _1} = 10Lo{g^{\frac{{{I_2}}}{{{I_1}}}}}\)
تراز شدت صوتی\(80db\) است. شدت این صوت چند وات بر متر مربع است؟ (\({I_0} = {10^{ - 12}}\frac{W}{{{m^2}}}\) )
\(\beta = 10Lo{g^{\frac{I}{{{I_0}}}}} \to 80 = 10Lo{g^{\frac{I}{{{{10}^{ - 12}}}}}} \to {10^8} = \frac{I}{{{{10}^{ - 12}}}} \to I = {10^{ - 4}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تن موسیقی
تن موسیقی
به صوت حاصل از چشمه ی صوتی كه به دليل ميرايی كم مشابه حركت هماهنگ ساده است، تن گفته می شود. (مانند صوت حاصل از يک دياپازون)
دو ويژگی مهم تن موسيقی
1) ارتفاع تن
ارتفاع، بسامدی است كه گوش انسان درک می كند.
2) بلندی تن
بلندی، شدتی است كه گوش انسان درک می كند.
1 ارتفاع و بلندی تن به ادراک شنوايی انسان مربوط است.
2 اگر به يک دياپازون ضربه هايی با قدرت های متفاوت بزنيم، بسامد صدايی كه می شنويم تغيير نمی كند اما صداهايی با بلندی متفاوت را حس می كنيم كه به شدت اين ضربه ها بستگی دارد.
3 بلندی با شدت متفاوت است. شدت را می توان با يک آشكارساز اندازه گيری كرد، اما بلندی چيزی است كه شما احساس می كنيد.
4 بيش ترين حساسيت انسان به بسامدهايی در گستره ی \(2000Hz\) تا \(5000Hz\) است. درحالی كه گوش انسان قادر به شنيدن تن های صدای \(20Hz\) تا \(20000Hz\) است.
اثر دوپلر
هنگامی كه چشمه ی صوتی و شنونده نسبت به هم دور يا نزديک شوند، بسامد و طول موجی كه شنونده دريافت می كند با بسامد و طول موج واقعی چشمه موج متفاوت است. به اين پديده اثر دوپلر گفته می شود.
بررسی حالت های مختلف اثر دوپلر
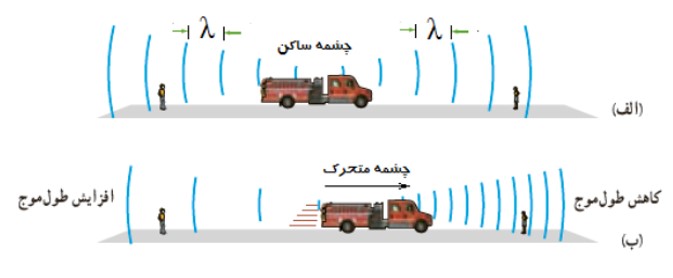
1) چشمه ی متحرک و ناظر (شنونده ی ساكن)
در اين حالت با توجه تصوير زير اگر چشمه ی موج به شنونده نزديک شود، طول موج كوتاه تر و اگر از آن دور شود طول موج بيش تر خواهد شد:
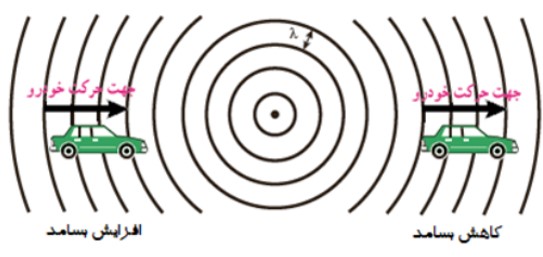
2) چشمه ساكن و ناظر (شنونده ) متحرک
در اين حالت تجمع جبهه های موج در دو سوی چشمه يكسان است. اگر ناظر به طرف چشمه حركت كند، در مقايسه با ناظر ساكن، در مدت زمان يكسان، با جبهه های موج بيش تری مواجه می شود كه اين منجر به افزايش بسامد صوتی می شود كه ناظر می شنود و اگر ناظر از چشمه دور شود، در مقايسه با ناظر ساكن، در مدت زمان يكسان، با جبهه های موج كم تری مواجه می شود كه اين منجر به كاهش بسامد صوتی می شود كه ناظر می شنود :
اثر دوپلر برای امواج الكترومغناطيس
بررسی اثر دوپلر در صوت با بررسی اثر دوپلر در امواج الكترومغناطيس متفاوت است. در بررسی اثر دوپلری برای موج الكترومغناطيس دو اصطلاح زير را به كار مي برند:
1) انتقال به سرخ
وقتی چشمه ی نور از ناظر (آشكار ساز) دور می شود، طول موج افزايش می يابد كه به آن انتقال به سرخ گفته می شود.
2) انتقال به آبی
وقتی چشمه ی نور به ناظر (آشكار ساز) نزديک می شود ، طول موج كاهش می يابد كه به آن انتقال به آبی گفته می شود.
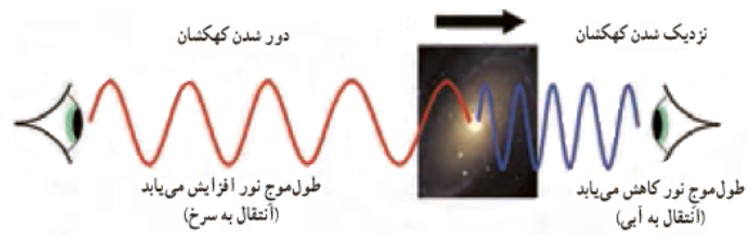
در رصد های نجومی ستارگان، كهكشان ها و ساير چشمه های نوری سماوی، چه هنگامی كه از ما دور می شوند چه هنگامی كه به ما نزديک می شوند، با اندازه گيری جابه جايی دوپلری آن ها می توان اطلاعاتی در مورد تندی و چگونگی حركت آن ها به دست آورد.



1736019749.png)