درسنامه کامل ریاضیات گسسته
تعداد بازدید : 515.21kخلاصه نکات ریاضیات گسسته - درسنامه شب امتحان ریاضیات گسسته - جزوه شب امتحان ریاضیات گسسته نوبت اول
انواعی از استدلال
فصل 1 : آشنایی با نظریۀ اعداد
انواعی از استدلال
گزاره
گزاره به يک حکم (يا ادعا) گفته می شود که يا دقيقاً درست و يا دقيقاً نادرست باشد.
اگر گزاره در تمام حالات ممکن درست باشد، گوييم آن گزاره درست است، ولی برای نادرست بودن آن، کافی است فقط در يک مورد نادرست شود.
بنابراين، در مواجهه با يک گزاره، در کل دو راه برای روشن کردن وضعيت آن وجود دارد.
رد کردن يا اثبات درستی
برايی رد يک ادعای کلی، روش زير را به کار می بريم.
مثال نقض
برای نشان دادن اينكه يک حكم کلی نادرست است، کافی است مثالی آورده شود كه كليت آن حكم را رد كند. به چنين مثالی، (مثال نقض) گفته می شود.
اگر بتوانيم برای يک حکم مثال نقض بياوريم، در واقع اثبات کرده ايم که آن حکم نادرست است.
مثال
درستی يا نادرستی گزاره ی زير را تعيين کنيد.
الف برای هر عدد طبيعی n بزرگتر از 1، عدد \({2^n} - 1\) اول است.
نادرست؛ عدد \(n = 4\) براي اين حكم يک مثال نقض است:
\(\begin{array}{l}{2^4} - 1 = 16 - 1 = 15\\ \to 15 = 3 \times 5\end{array}\) اول نیست.
ب مجموع دو عدد گنگ عددی گنگ است.
نادرست است و مثال نقض دارد، عدد های \(a = \sqrt 2 \) و \(b = - \sqrt 2 \) هر دو گنگ هستند ولی جمعشان گویا است:
\(a + b = \sqrt 2 - \sqrt 2 = 0 \in \mathbb{Q}\)
مثالی که برای نقض يک حکم کلی آورده می شود، بايد دارای شرط زير باشد:
فرض عبارت داده شده را برقرار سازد، ولی حکم آن عبارت نادرست شود.
مثال
1 حكم (حاصل جمع سه عدد گنگ، عددی گنگ است.) را با مثال نقض رد کنيد.
بايد سه عدد گنگ ارائه دهيم كه جمعشان گنگ نشود (گويا باشد). عددهای گنگ \(3 - 2\sqrt 2 ,\sqrt 2 + 2,\sqrt 2 - 1\) این شرایط را دارند؛
\(3 - 2\sqrt 2 + \sqrt 2 + 2 + \sqrt 2 - 1 = 4\)
2 هيچ دو عدد صحيح مانند x و y وجود ندارد که تساوي \({x^2} - {y^2} = {(x + y)^2}\) برقرار باشد.
نادرست است و مثال نقض دارد، عدد های \(x = 1\) و \(y = 0\) وجود دارند؛
\({x^2} + {y^2} = {1^2} + {0^2} = 1 + 0 = 1\) و \({(x + y)^2} = {(1 + 0)^2} = {1^2} = 1\)
ممکن است با بررسی مثال های گوناگون، نتوانيم هيچ مثال نقضی پيدا کنيم و تمام مثال های آورده شده، حکم را تاييد کنند. در اين صورت، توجه کنيد:
- هر تعداد مثال در تاييد يک حکم آورده شود، باعث اثبات آن نخواهد شد، چون امکان دارد مثال بعدی، يک مثال نقض باشد.
- وقتی چندين مثال يک حکم را تاييد می کنند، احتمال درست بودن حکم معمولاً بيشتر می شود.
روش نتيجه گيری با بررسی چند مثال و مشاهده ی درستی حکم را (استدلال استقرايی) گويند. اين روش در علوم تجربی کاربرد فراوان دارد. اما در ریاضیات بعد از به کار بردن استدلال استقرايی، حکم را به عنوان يک (حدس) يا (فرضيه) می پذيريم.
برای اينکه فرضيه يا حدس تاييد قطعی شود، نياز به اثبات دارد که توسط دو مؤلفه ی زير انجام می شود.
حقايق پذيرفته شده
اصول و احکامی که قبلاً درستی آنها پذيرفته يا اثبات شده است.
روش های درست استنتاج
معمولاً حقايق پذيرفته شده ی قبلی با روش های درست استدلال، مفروضات مسأله را به کار می برنـد تـا يـک حکـم جديـد اثبات شود.
حقايق پذيرفته شده
برخی حقايق پذيرفته شده که در اثبات ها بيشتر به کار می روند را ببينيد:
هر عدد زوج به صورت \(2k\) و هر عدد فرد به صورت \(2k - 1\) است.
هر عدد گويا را ميتوان به صورت کسر \(\frac{m}{n}\) نوشت که m و n دو عدد صحيح بوده و مخرج غير صفر است.
هر عددی که نتوان آن را به صورت کسر گويا نوشت، گنگ است.
روش های اثبات
می توان روش های اثبات احکام رياضی را در دو نوع کلی طبقه بندی کرد:
اثبات مستقيم و اثبات غيرمستقيم
اثبات مستقيم
در روش هايی که در اين گروه جای می گيرند، فرض مسأله و حقايق قبلی به طور مناسب به کار رفته، حکم تاييد می شود و اثبات صورت می پذيرد.
اثبات غير مستقيم
در اين گروه از روش های اثبات، به نوعی حکم مسأله و حقايق قبلی را مورد استفاده قرار داده و درسـت بـودن حکـم را نتيجه می گيريم.
مثال
1 نشان دهيد مربع هر عدد زوج، زوج و مربع هر عدد فرد هم فرد است.
اگر n عددی زوج باشد:
\(n = 2k \to {n^2} = 4{k^2} = 2 \times 2{k^2} = 2k' \to {n^2} = 2k'\)
اگر n عددی فرد باشد:
\(n = 2k + 1 \to {n^2} = 4{k^2} + 4k + 1 = 2 \times (2{k^2} + 2k) + 1 = 2k' + 1 \to {n^2} = 2k' + 1\)
2 نشان دهيد نتيجه گيری زير برای اعداد درست است.
\(ab = 0 \Rightarrow a = 0 \vee b = 0\)
اگر \(a = 0\) باشد، نتیجه گیری برقرار شده است.
اگر \(a \ne 0\) باشد، در این صورت \(\frac{1}{a}\) وجود دارد و طبق فرض:
\(ab = 0 \Rightarrow \frac{1}{a} \times ab = \frac{1}{a} \times 0 \Rightarrow 1 \times b = 0 \Rightarrow b = 0\)
پس نتیجه گیری همواره درست است.
برسی تمام حالات
گاهی استفاده از تکنيک زير، در اثبات مستقيم احکام مورد نياز است:
تفکیک فرض به تمام حالت های ممکن، و بررسی درستی حکم در هر حالت.
به هم ارزی زير بين گزاره ها توجه کنيد:
\(\begin{array}{l}({P_1} \vee {P_2} \vee ... \vee {P_K}) \Rightarrow q \Leftrightarrow \sim ({P_1} \vee {P_2} \vee ... \vee {P_K}) \vee q\\ \Leftrightarrow ( \sim {P_1} \wedge \sim {P_2} \wedge ... \wedge \sim {P_K}) \vee q\\ \Leftrightarrow ( \sim {P_1} \vee q) \wedge ( \sim {P_2} \vee q) \wedge ... \wedge ( \sim {P_K} \vee q)\\ \Leftrightarrow ({P_1} \Rightarrow q) \wedge ({P_2} \Rightarrow q) \wedge ... \wedge ({P_K} \Rightarrow q)\end{array}\)
یعنی اگر فرض در کل به حالت های \({P_2},{P_1}\) ... و \({P_K}\) تفکيک شده و هرکدام از آن ها درستی q را نشان دهند. درستی q در کل اثبات می گردد.
در ادامه، دو روش در اثبات غير مستقيم و نمونه هايی از هر کدام ببينيد:
برهان خلف
برای استفاده از اين روش، طبق گام های زير عمل می کنيم:
حكم مورد نظر را نادرست در نظر می گيريم؛ يعنی فرض می کنيم حکم نادرست باشد.
با توجه به فرض مرحله ی قبل و بيان استدلالی مناسب، (حقايق شناخته شده) يا (فرض) آن قضيه يا مسأله را نقض می كنيم.
نتيجه می گيريم حكم آن مسأله نمی تواند نادرست باشد و از ابتدا صحيح بوده است.
مثال
1 نشان دهید اگر \({n^2}\) فرد باشد، آنگاه n هم فرد است.
با برهان خلف پیش می رویم؛ فرض كنيد n فرد نباشد. پس n زوج است و چنان كه قبلاً ديديم، بايد\({n^2}\) هم زوج باشد كه با فرض تناقض دارد. پس حكم نمی تواند نادرست باشد و لذا صحيح خواهد بود.
2 اگر \(\alpha \) و \(\beta \) دو عدد گنگ و \(\alpha + \beta \) گویا باشد، نشان دهید عدد \(\alpha + 2\beta \) گنگ است.
با برهان خلف پیش می رویم:
اگر \(\alpha + 2\beta \) گویا باشد، چون تفریق دو عدد گویا، گویا است:
\(\alpha + 2\beta - (\alpha + \beta ) = \beta \) گویا
گویا بودن \(\beta \) با فرض تناقض دارد.
اثبات بازگشتی
در اثبات به طريق بازگشتی به ترتيب زير عمل می کنيم:
درستی حكم را موقتاً می پذيريم.
با شروع از حکم، در چند مرحله به يک رابطه ی بديهی يا فرض داده شده می رسيم.
اکنون اگر تمام مراحل را بتوان از آخر به اول نتيجه گرفت، يعنی اعمال انجام شده برگشت پذير باشـند، درسـتی حكم تأييد می شود.
يک استنتاجِ درست، ممکن است برگشت پذير باشد يا نباشد؛ نمونه ای ببينيد:
استنتاج (\(x = 2 \to {x^2} = 4\) )برگشت پذیر نیست؛ زیرا نتیجه گیری (\({x^2} = 4 \to x = 2\) )
مثال
1 به روش بازگشتی ثابت کنيد: حاصل ضرب هر دو عدد حقيقی، کوچکتر يا مساوی نصف مجموع مربعات آنها است.
باید ثابت کنیم: \(xy \le \frac{{{x^2} + {y^2}}}{2}\)
\(xy \le \frac{{{x^2} + {y^2}}}{2} \to \times 2 \to 2xy \le {x^2} + {y^2} \to 0 \le {x^2} + {y^2} - 2xy \to 0 \le {(x + y)^2}\)
چون نامساوی آخر هميشه صحيح بوده و مراحل بالا برگشتپذير هستند، اثبات كامل است.
2 نامساوی \(a + \frac{1}{a} \ge 2\) را در \(a\rangle 0\) نشان دهید.
کافی است دو طرف حکم \(a + \frac{1}{a} \ge 2\) را در \(a\rangle 0\) ضرب کنیم:
\(a + \frac{1}{a} \ge 2 \to \times a \to {a^2} + 1 \ge 2a \to {a^2} - 2a + 1 \ge 0 \Rightarrow \left( {a - 1} \right) \ge 0\)
عبارت \(\left( {a - 1} \right) \ge 0\) همواره درست است و بعلاوه تمام مراحل بالا برگشت پذير هستند.
وقتی از برگشت پذيری استنتاج ها اطمينان داريد، بهتر است به جای استفاده از نماد \( \to \)، نماد \( \leftrightarrow \) را به کار ببرید.
گزاره ی درست را اثبات کرده و برای گزاره ی نادرست مثال نقض بياوريد.
الف مجموع دو عدد گنگ، عددی گنگ است.
نادرست است و مثال نقض دارد، عدد های \(a = \sqrt 2 \) و \(b = - {\kern 1pt} \sqrt 2 \) هر دو گنگ هستند، ولی جمعشان گویا است؛
\(\begin{array}{l}a + b = \sqrt 2 - \sqrt 2 = 0\\0 \in \mathbb{Q}\end{array}\)
ب اگر \(\alpha \) و \(\beta \) دو عدد گنگ و \(\alpha + \beta \) گویا باشد، نشان دهید عدد \(\alpha + 2\beta \) گنگ است.
با برهان خلف پیش می رویم؛ اگر \(\alpha + 2\beta \) گویا باشد، چون تفریق دو عدد گویا، گویا است؛ \(\alpha + 2\beta - (\alpha + \beta ) = \beta \) گویا بودن \(\beta \) با فرض تناقض دارد.
تهیه کننده: علیرضا نورالدّینی
- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته
بخش پذیری در Z
فصل 1 : آشنایی با نظریۀ اعداد
بخش پذیری در Z
به بيان دقيق مفهوم (بخش پذيری) در اعداد صحيح توجه کنيد:
بخش پذيری
فرض کنید a و \(b \ne 0\) عددهایی صحیح باشند.
عدد a را بر b(بخش پذير) گوييم، هرگاه عدد صحيح k يافت شود كه \(a = bk\) در این صورت می نویسیم: \(b|a\)
برای نمونه
داریم: \(4| - 12\) ، زیرا عدد \( - 12\) را می توان به صورت \(4( - 3)\) نوشت.
عبارت \(b|a\) به صورت b عاد می کند a را يا b عدد a را می شمارد، خوانده می شود. (b یک شمارنده یا مقسوم علیه a است.)
خواص مقدماتی
تمام اعداد بر 1 و \( - 1\) بخش پذير هستند؛ يعنی همواره: \( \pm 1|a\)
زیرا
\(a = 1 \times a \to 1|a,a = - 1 \times ( - a) \to - 1|a\)
تمام اعداد صحيح، عدد صفر را عاد می کنند، زيرا \(0 = a \times 0\) به عبارت دیگر؛ صفر تنها عددی است که بر تمام اعداد بخش پذير است، يعنی همواره، \(a|0\) .
هيچ عددی بر صفر بخش پذير نيست. ولی چون تساوی \(0 = 0 \times k\) برای هر عدد صحیح k برقرار است، خواهیم داشت \(0|0\) بنابراین:
\(0|a \Rightarrow a = 0\)
يعنی عدد صفر فقط خودش را عاد می کند.
هر عددی بر خودش بخش پذير است؛ زيرا:
\(a = a \times 1 \Rightarrow a|a\)
به صورت مشابه، موارد \(a| - a\) و \( - a|a\) نيز درست هستند. يعنی \( \pm a| \pm a\)
مثال
1 نشان می دهيم برای هر عدد طبيعی n داريم:
\(a|{a^n}\)
در حالت \(n = 1\) ، رابطه ی بدیهی \(a|a\) را داريم که درست است. اگر \(n\rangle 1\) باشد، در این صورت:
\({a^n} = a \times {a^n} - 1 \to {a^n} = ak \Rightarrow a|{a^n}\)
2 نشان می دهيم اگر \(a|b\) ، آنگاه برای هر عدد طبیعی n داریم:
\({a^n}|{b^n}\)
حالت \(n = 1\) بدیهی است. اگر \(n\rangle 1\) باشد، چون \(b = ak\) است، در این صورت:
\(bn = {\left( {ak} \right)^n} = {a^n} \times {k^n} \to {k^n} = k' \to {b^n} = {a^n}k' \Rightarrow {a^n}|{b^n}\)
يادآوری يک مفهوم بسيار پرکاربرد در مبحث نظريه اعداد:
عدد اول
عدد طبیعی \(p\rangle 1\) را اول گوییم. هرگاه غير از 1 و خودش هيچ مقسوم عليه مثبتی نداشته باشد. بنابراين، اگر p عددی اول باشد:
\(a|p \Rightarrow a = \pm 1,a = \pm p\)
ساير اعداد طبيعی بزرگ تر از يک را (مركب) گوييم. بنابراين:
عدد ١ نه اول است و نه مركب.
در ادامه ويژگی های اصلی شمارش، دليل هر کدام و برخی کاربردهای آنها را ببينيد.
1) اگر a عدد b را عاد کند، aهر مضربd از b را نيز عاد می کند؛ يعنی برای هر عدد صحيح m :
\(a|b \Rightarrow a|bm\)
برای نمونه؛
\(5|10 \Rightarrow 5|20,5| - 10,5|50,...\)
2) شمارش، خاصيت تعدی دارد. يعنی اگر a بر b و b بر c بخش پذير باشد، آنگاه:a بر c بخش پذير است.
با صورت نمادين
\(c|b \wedge b|a \Rightarrow c|a\)
برای نمونه؛
از این که \(6|12\) و \(12|48\) می توان نتیجه گرفت: \(6|48\)
برای عددهای صحيح a و b ، با توجه به تجزيه ی عبارت های \({a^n} \pm {b^n}\)
\(\begin{array}{l}{a^n} - {b^n} = (a - b)({a^{n - 1}} + {a^{n - 2}}b + ... + a{b^{n - 2}} + {b^{n - 1}})\\{a^n} + {b^n} = (a + b)({a^{n - 1}} + {a^{n - 2}}b + ... - a{b^{n - 2}} + {b^{n - 1}})\end{array}\)
همواره رابطه ی \(a - b|{a^n} - {b^n}\) برقرار است.
3) اين ويژگی به صورت زير بيان می شود:
اگر دو عدد بر عددی بخش پذير باشند، آنگاه جمع و تفريق آنها هم بر آن عدد بخش پذير است.
با نماد رياضی:
\(a|b \wedge a|c \Rightarrow a|b \pm c\)
4) اگر داشته باشيم \(a|b\) و \(b \ne 0\) باشد، آنگاه \(\left| a \right| \le \left| b \right|\) به صورت نمادین:
\(a|b \wedge b \ne 0 \Rightarrow \left| a \right| \le \left| b \right|\)
به بیان ساده؛ يک عدد مثبت نمی تواند بر عددهای بزرگتر از خود بخش پذير باشد. زیرا:
طبق فرض، عدد \(k \in \mathbb{Z} - \{ 0\} \) هست که \(b = ak\) در نتیجه:
\(\left| b \right| = \left| a \right|\left| k \right| \to \left| k \right| \ge 1 \to \left| b \right| \ge \left| a \right|\)
مثال
1 نشان دهید مربع هر عدد فرد به صورت \(8K + 1\) است.
فرض کنید n عددی فرد باشد، پس؛ \(n = 2q + 1\) و خواهیم داشت:
\({n^2} = {\left( {2q + 1} \right)^2} = 4{q^2} + 4q + 1 = 4q\left( {q + 1} \right) + 1 \to q\left( {q + 1} \right) = 2k \to 8k + 1\)
بيان مهم ديگری از حکم اين مثال چنين است:
(باقی مانده ی تقسيم مربع هر عدد فرد بر 8 برابر 1 است.)
2 نشان دهید اگر k عددی زوج باشد، \({k^3} - 4k\) همواره مضرب 48 است.
می نویسیم \(k = 2n\) و طبق خاصیت گفته شده برای ضرب 3 عدد متوالی:
\({k^3} - 4k = {\left( {2n} \right)^3} - 4\left( {2n} \right) = 8{n^3} - 8n = 8n\left( {{n^2} - 1} \right) = 8n\left( {n - 1} \right)\left( {n + 1} \right) \to n\left( {n - 1} \right)\left( {n + 1} \right) = 6q \to 8n\left( {n - 1} \right)\left( {n + 1} \right) = 48q\)
قضیه تقسیم
در تقسيم عدد صحيح a بر عدد طبيعی b ، اعداد صحيح و يكتای q و r وجود دارند که:
\(\begin{array}{l}a = bq + r\\0 \le r\langle b\end{array}\)
عددهای q و r به ترتيب (خارج قسمت) و (باقيمانده) تقسيم a بر b نام دارند.
در تقسيم a بر b همواره می توان:
خارج قسمت را توسط جزء صحيح \(q = \left[ {\frac{a}{b}} \right]\) و سپس؛ باقيمانده را از رابطه ی \(r = a - bq\) به دست آورد.
دسته بندی اعداد صحیح
فرض کنید \(m\rangle 1\) عدد طبيعی ثابتی باشد. عدد صحيح دلخواه a را در نظر گرفته و آن را بر m تقسيم می کنيم:
\(\begin{array}{l}a = mk + r\\r = 0,1,2,...,m - 1\end{array}\)
می بينيد که می توان عددهای صحيح را بر حسب باقيمانده تقسيم بر m در يک مجموعه قرار داد.
اگر باقيمانده صفر باشد، عددها به صورت زير هستند:
\(a = mk,k \in \mathbb{Z}\)
مجموعه ی تمام اين نوع اعداد را با \({[0]_m}\) نشان می دهیم:
\({[0]_m} = \{ mk|k \in \mathbb{Z}\} \)
اگر باقيمانده ی تقسيم برابر 1 شود، عددها به اين صورت هستند:
\({[1]_m} = \{ mk + 1|k \in \mathbb{Z}\} \)
ساير عددهای صحيح نيز به يکی از صورت های زير خواهند بود:
\(\begin{array}{l}{[2]_m} = \{ mk + 2|k \in \mathbb{Z}\} \\{[3]_m} = \{ mk + 3|k \in \mathbb{Z}\} \\.\\.\\{[m - 1]_m} = \{ mk + m - 1|k \in \mathbb{Z}\} \end{array}\)
بنابراين:
با انتخاب عدد طبيعی m ، مجموعه ی \(\mathbb{Z}\) دقيقاً به تعداد m زير مجموعه افراز می شود:
\({[0]_m},{[1]_m},{[2]_m},...,{[m - 1]_m}\)
یعنی
- اين مجموعه ها هيچکدام تهی نيستند.
- دو به دو اشتراک ندارند.
- هر عدد صحيح در يکی از آنها جای دارد.
هر عدد صحيح a بر حسب عدد طبيعی m به يكی از صورت های زير قابل نوشتن است:
\(mk,mk + 1,mk + 2,...,mk + m - 1\)
مثال
نشان دهيد برای عدد صحيح فرد a ، عدد \({a^4}\) به صورت \(16k + 1\) است.
می دانیم که كه مربع هر عدد فرد به صورت \(8k + 1\) ست، پس می توان نوشت:
\(a4 = {({a^2})^2} = {(8k + 1)^2} = 64{k^2} + 16k + 1 = 16(4{k^2} + k) + 1\)
ثابت کنيد اگر \(p \ge 5\) عددی اول باشد، آنگاه به يکی از دو صورت \(p = 4k + 1\) یا \(p = 4k + 3\) نوشته می شود.
عدد p در تقسيم بر 4 به يكی از چهار حالت زير است:
\(4k,4k + 1,4k + 2,4k + 3\)
در دو حالت زير،p اول نيست:
\(p = 4k:\)
چون p بر 2 بخش پذير است.
\(p = 4k + 2:\)
در اين صورت \(p = 2(2k + 1)\) بوده و باز هم بر 2 بخش پذير است.
در نتيجه:
p فقط می تواند به صورت \(4k + 1\) یا \(4k + 3\) باشد.
تهیه کننده: علیرضا نورالدّینی
ب.م.م و ک.م.م
فصل 1 : آشنایی با نظریۀ اعداد
ب.م.م و ک.م.م
دو مفهوم ب.م.م و ک.م.م کاربردهای زيادی در نظريه اعداد دارند.
ب.م.م اعداد
فرض كنيد a و b دو عدد صحيح باشند كه لااقل یكی از آنها غيـر صـفر اسـت. عـدد طبيعـی d را (ب.م.م) يعنـی بزرگترين مقسوم عليه مشترک اين دو عدد گوئيم، هرگاه:
1) \(d|b,d|a\)
2) ساير مقسوم عليه های مشترک a و b از d كوچكتر باشند. در اين صورت می نويسيم:
\((a,b) = d\)
در حالت خاص:
اگر \(a|b\) ، آنگاه \((a,b) = \left| a \right|\) است. به ویژه:
\((a,a) = \left| a \right|,(a,0) = \left| a \right|\)
البته عبارت \((0,0)\) بی معنی است.
حالت خاص زير در مورد ب.م.م اعداد اهميت بسياری دارد.
اعداد متباين:
دو عدد a و b را نسبت به هم اول يا (مُتَبايِن) گوئيم، هرگاه:
\((a,b) = 1\)
به دو مورد در ارتباط با اين مفهوم توجه کنيد:
واضح است که \((4,9) = 1\) و بنابراين متباين بودن اعداد ربطی به اول بودن تک تک آنها ندارد.
ولی عکس آن صحيح است:
اگر p و q دو عدد اول مختلف باشند، همواره: \((p,q) = 1\) .
دو عدد a و b وقتی نسبت به هم اول هستند که در تجزيه ی اين دو عدد به عددهای اول، عامـل اول مـشترکی وجود نداشته باشد. برای نمونه؛
چون \(35 = 5 \times 7,48 = {2^2} \times 3\) ، بنابراین \((48,35) = 1\) است.
مثال
1 نشان دهيد عدد 77 نسبت به هر سه عدد 64، 81 و 125 اول است.
تجزيه ی اين عددها به صورت زير است:
\(77 = 7 \times 11,64 = {2^6},81 = {3^4},125 = {5^3}\)
چون 77 با هيچ كدام عامل مشترک ندارد، نسبت به همه ی آنها اول است.
2 نشان دهيد دو عدد فرد متوالی همواره نسبت به هم اول هستند.
دو عدد فرد متوالی به صورت \(2n + 1\) و \(2n + 3\) هستند. قرار می دهیم: \(\left( {2n + 1,2n + 3} \right) = d\) . طبق تعریف:
\(\begin{array}{l}d|2n + 1\\d|2n + 3\\ \to - \to d|2n + 3 - \left( {2n + 1} \right) \to d|2 \to d = 1 \vee d = 2\end{array}\)
چون عدد ها فرد هستند، \(d = 2\) غیرممکن بوده و در نتیجه \(\left( {2n + 1,2n + 3} \right) = 1\) است.
اکنون مضرب های مشترک دو عدد صحيح را بررسی می کنيم:
ک.م.م اعداد
فرض كنيم a و b دو عدد صحيح باشند كه هر دو غير صفر هستند. عدد طبيعـی c را (ک.م.م) يعنـی کوچـکتـرين مضرب مشترک اين دو عدد گوئيم، هرگاه:
1) \(b|c,a|c\)
2) ساير مضرب های مثبت و مشترک a و b از c بزرگتر باشند. در اين صورت می نويسيم:
\([a,b] = c\)
در يک حالت خاص
هر گاه \(a|b\) ، آنگاه \([a,b] = \left| b \right|\) است؛ به ویژه:
\([a, \pm a] = |a|,[ \pm 1,a] = |a|\)
مثال
برای دو عدد صحيح غير صفر a و b ، مقادير زير را حساب کنيد.
\([a,(a,b)],(a,[a,b])\)
چون \((a,b)|a,a|[a,b]\) ، جواب دو مورد برابر \(|a|\) است.
اگر عددهای داده شده را تجزيه کنيد، در اين صورت:
- ب.م.م. برابر ضرب عامل های مشترک با توان کوچکتر است.
- ک.م.م. برابر ضرب عامل های مشترک با توان بزرگتر ضربدر تمام عامل های غير مشترک است.
تکنیک \(a'\) و \(b'\)
ابتدا توجه کنيد:
اگر a و b دو عدد صحيح و \((a,b) = d\) باشد، آنگاه \((\frac{a}{d},\frac{b}{d}) = 1\) است.
اکنون فرض کنيد \((a,b) = d\) باشد، آنگاه:
قرار می دهيم: \(\frac{b}{d} = b',\frac{a}{d} = a'\)
طبق مرحله ی قبل خواهيم داشت: \(a = a'd\) و \(b = b'd\) و البته \((a',b') = 1\)
به جای اينکه دنبال اعداد نسبتاً بزرگ a و b بگرديد، بهتر است دنبال عددهای کوچکتر و متباين \(a'\) و \(b'\) بگردید.
ک.م.م بر حسب \(a'\) و \(b'\)
ک.م.م برابر \([a,b] = a'b'd\) است، زیرا:
\([a,b] = \frac{{a'd \times b'd}}{d} \Rightarrow [a,b] = a'b'd\)
اگر \((a,b) = 1\) باشد، آنگاه \([a,b] = |ab|\)
اگر a و b اعدادی صحيح باشند، آنگاه نشان دهيد \((ab + 1,a) = 1\) .
قرار می دهیم: \((ab + 1,a) = d\)
طبق تعريف بايد \(d|a\) و لذا d هر مضرب a از جمله ab را عاد می كند. بنابراين:
\(\begin{array}{l}d|ab\\d|ab + 1\\ \to d|ab + 1 - d|ab \to d|1 \to d = 1\end{array}\)
تهیه کننده: علیرضا نورالدّینی
معرفی گراف
فصل 2 : گراف و مدل سازی
معرفی گراف
گراف از مجموعه ای از نقاط (که به هر کدام راس می گوییم) و مجموعه ای از خطوط (که به هرکدام یال می گوییم) تشکیل شده است. هر یال بین دو راس قرار دارد. در گراف G مجموعه ی راس ها را با (Vertex) V (G) و مجموعه یال ها را با (Edge) E (G) نشان می دهیم.
گراف یک روش مدل سازی برای نشان دادن رابطه بین اعضای یک مجموعه است.
مثال
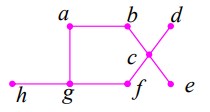
1 برای گراف زیر یک مجموعه ی احاطه گر بنویسید.
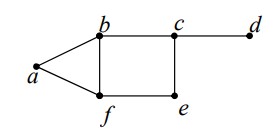
\(\{ a,b,e,d\} \)
2 یک گراف 5 راسی با عدد احاطه گری 2 رسم کنید.
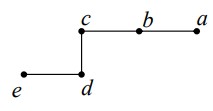
به گرافی که یال های آن جهت داشته باشند، گراف جهت دار می گوییم. در نمایش گراف جهت دار با استفاده از نماد های ریاضی، یال هارا با زوج مرتب نشان می دهیم.
مثال
مجموعه ی راس ها و یال های گراف زیر را بنویسید.
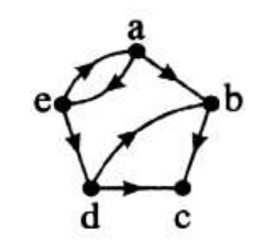
\(\begin{array}{l}V = \{ a,b,c,d,e\} \\E = \{ (a,b),(b,c),(d,c),(d,b),(e,d),(e,a),(a,e)\} \end{array}\)
برای رسم نمودار یک گراف روش یکتایی وجود ندارد و شکل گراف صرفا باید مشخص کند که کدام راس ها به هم متصل اند.
مثلا دو نمودار زیر هر دو یک گراف را نمایش می دهند.
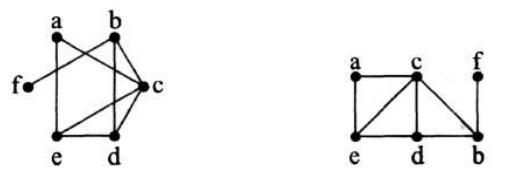
بین هر دو راس گراف ممکن است بیش از یک یال موجود باشد و همچنین یک یال ممکن است یک راس را به خود آن راس وصل کند که در این صورت به آن یال طوقه می گویند.
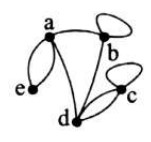
به گرافی که طوقه نداشته باشد و بین هر دو راس آن حداکثر یک یال وجود داشته باشد، گراف ساده می گوییم. در این فصل با گراف های ساده سر و کار خواهیم داشت و هر کجا از گراف نام ببریم، منظور گراف ساده است.
مرتبه و اندازه گراف
به تعداد راس های گراف G، مرتبه ی گراف گفته و آن را با P نشان می دهیم. به تعداد یال های گراف G، اندازه ی گراف گفته و آن را با q نشان می دهیم.
تعریف درجه راس گراف
به تعداد یال های متصل به گراف G که به راس V متصل اند، درجه ی آن راس گفته و آن را با \({\deg _G}(v)\) یا \(\deg (v)\) نشان می دهیم. اگر درجه یک راس عددی فرد باشد، به آن راس فرد و اگر درجه زوج باشد، به آن راس زوج می گوییم. در صورتی که \(\deg (v) = 0\) باشد (یعنی راس مورد نظر به راس دیگر متصل نباشد) به v راس تنها یا ایزوله می گوییم.
دو راس مجاور
دو راس که توسط یالی به هم متصل شده باشند را مجاور (یا همسایه) می نامیم. مثلا در گراف زیر راس های مجاور و غیر مجاور عبارت اند از:
مجموعه های همسایه های یک راس
فرض کنیم \(v \in V(G)\)، به مجموعه راس هایی از گراف g که به راس v متصل هستند، همسایگی باز راس v می گوییم و با \({N_G}(v)\) نمایش می دهیم. اضافه کردن خود راس v به \({N_G}(v)\) همسایگی بسته ی راس v را به دست می دهد که آن را با \({N_G}[v]\) نمایش می دهیم. می توان این دو مجموعه را به صورت زیر نشان داد:
\(\begin{array}{l}{N_G}(v) = \{ u \in V(G):uv \in E(G)\} \\{N_G}[v] = {N_G}(v) \cup \{ v\} \end{array}\)
مثال
مجموعه های همسایه های یک راس گراف زیر را بنویسید.
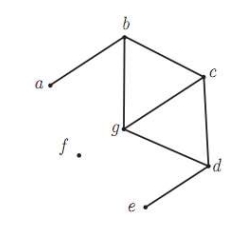
\(\begin{array}{l}{N_G}(a) = \{ b\} \\{N_G}(c) = \{ b,d,g\} \\{N_G}(f) = \emptyset \\{N_G}[a] = \{ a,b\} \\{N_G}[c] = \{ b,c,d,g\} \\{N_G}[f] = \{ f\} \end{array}\)
در صورتی که \({N_G}[v] = \emptyset \) باشد، راس v ایزوله است.
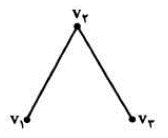
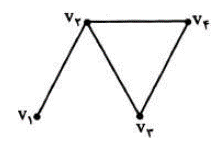
دو یال مجاور
دو یال را مجاور می نامیم هر گاه راسی وجود داشته باسد که هر دو یال به آن وصل باشند. مثلا در گراف زیر یال های \({v_1}{v_2}\) و \({v_2}{v_3}\) مجاورند. ولی یال های \({v_1}{v_2}\) و \({v_3}{v_4}\) مجاور نیستند.
بزرگ ترین و کوچک ترین درجه گراف
بزرگ ترین درجه در بین راس های یک گراف را ماکزیمم درجه نامیده و آن را با نماد \(\Delta (G)\) نمایش می دهیم. به صورت مشابه، کوچک ترین درجه را مینیمم درجه نامیده و با نماد \(\delta (G)\) نمایش می دهیم.
برای مثال در گراف زیر \(\Delta = 3\) و \(\delta = 1\)
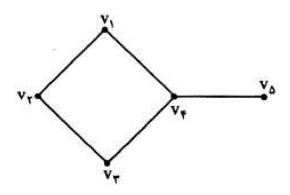
حواستان باشد ممکن است چند راس از درجه ماکسیمم یا مینیمم وجود داشته باشد.
همواره داریم \(\Delta \le p - 1\)
در گراف از مرتبه p، راسی که با همه رئوس دیگر مجاور باشد، را راس فول (پر) می نامیم. در واقع راس فول دارای درجه \(p - 1\) است.
اگر گرافی از مرتبه p، دارای k راس فول باشد آنگاه \(\delta \ge K\)
ارتباط درجه راس ها با تعداد یال ها
فرض کنید گراف G از مرتبه ی p و اندازه ی q باشد، در این صورت:
\(\sum\limits_{i - 1}^p {\deg ({v_i}) = } \deg ({v_1}) + \deg ({v_2}) + ... + \deg ({v_p}) = 2q\)
در نتیجه تعداد راس های فرد هرگراف عددی زوج است.
تمرین
1 در گراف شکل زیر
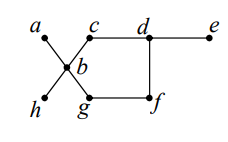
الف) مجموعه احاطه گری بنویسید که مینیمال باشد ولی مینیمم نباشد.
\(\{ a,h,c,e,f\} \)
ب) عدد احاطه گری این گراف را تعیین کنید.
\(\left[ {\frac{8}{{4 + 1}}} \right] = 2 \le \gamma (G)\) و چون \(\{ b,d\} \) یک مجموعه ی احاطه گر پس \(\gamma (G) = 2\)
2 شهری دارای 11 میدان است و هر میدان شهر از طریق خیابان ها حداکثر به 4 میدان دیگر متصل است. می خواهیم در بعضی از میدان ها نمازخانه بسازیم به طوری که هر شخصی در هر یک از میدان های شهر که باشد، یا در همانی میدانی که ایستاده به نمازخانه دسترسی داشته باشد یا در میدان مجاور آن. آیا با ساخت 2 نمازخانه می توانیم به این هدف برسیم؟ چرا؟
چون کران پایین عدد احاطه گری 3 است. پس با تعداد کمتر از 3 نمازخانه به هدف نمی رسیم و حداقل به 3 نماز خانه لازم است.
\(\gamma (G) = \left[ {\frac{{11}}{{4 + 1}}} \right] = 3\)
تهیه کننده: جابر عامری و الماسی کیا
- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته
انواع گراف
فصل 2 : گراف و مدل سازی
انواع گراف
گراف های منتظم
گرافی که درجه ی همه راس های آن r باشد، گراف r-منظم (از مرتبه p) نامیده می شود. برای نمونه گراف های زیر 2-منتظم و 3-منتظم هستند:
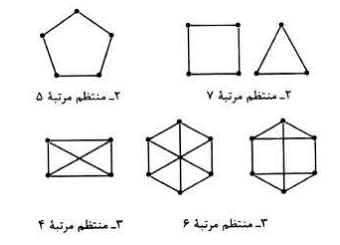
گفتیم هر گراف، مجموع درجه ها برابر  می شود. حال در گراف r-منتظم p راسی داریم:
می شود. حال در گراف r-منتظم p راسی داریم:
مجموع درجه ها = \(r + r + ... + r = 2q \Rightarrow pr = 2q\)
یعنی در گراف های منتظم ضرب مرتبه در درجه راس ها، دو برابر تعداد یال ها می شود.
یعنی pr همواره عددی زوج است؛ پس p و r نمی توانند هر دو فرد باشد (یعنی گراف فرد-منتظم از مرتبه فرد نداریم).
مثال
1 یک گراف 2-منتظم 5 راسی رسم کنید که دارای بیش از یک مجموعه ی احاطه گر مینیمم با اندازه 2 باشد. حداقل دو تا از مجموعه های احاطه گر مینیمم آن را بنویسید.
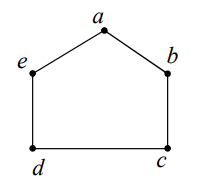
مجموعه های احاطه گر مینیمم، مجموعه های زیر می باشند.
\(\{ a,c\} ,\{ a,d\} \)
2 یک گراف 8 راسی با عدد احاطه گری 2 رسم کنید که دارای فقط یک مجموعه ی احاطه گر باشد.
در گراف زیر تنها مجموعه ی \(\{ c,g\} \) احاطه گر مینیمم می باشد.
گراف های کامل
گرافی از مرتبه ی p که هر دو راس آن مجاور باشند را گراف کامل نامیده و با \({K_p}\) نشان می دهیم.
در واقع گراف های کامل حداکثر تعداد یال ها را در مرتبه ی خود دارند و دیگر نمی توانیم به آن ها یال اضافه کنیم.
در جدول زیر گراف های کامل تا مرتبه 5 را مشاهده کنید:
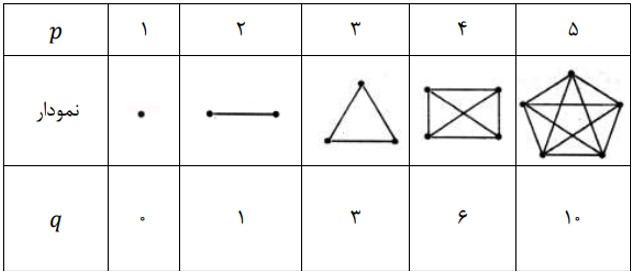
1 درجه ی هر راس در گراف کامل p راسی \(p - 1\) است. یعنی گراف کامل \({K_p}\)، یک گراف \(p - 1\) منتظم است.
2 تعداد یال ها در گراف کامل p راسی برابر است با:
مجموع درجه ها = \((p - 1) + (p - 1) + ... + (p - 1) = 2q \Rightarrow q = \frac{{p(p - 1)}}{2}\)
مکمل گراف
مکمل گراف G که آن را با \({G^c}\) یا \(\bar G\) نشان می دهیم، گرافی است که مجموعه راس های آن همان مجموعه ی راس ها است و دو راس در \(\bar G\) مجاورند اگر در G مجاور نباشند. برای مثال در شکل زیر یک گراف کامل و مکمل آن را می بینید:
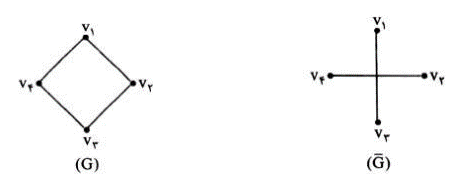
اگر تعداد یال های G و \(\bar G\) را با هم جمع کنیم، برابر تعداد یال های گراف کامل می شود؛ یعنی:
\(q(G) + q(\bar G) = \frac{{p(p - 1)}}{2}\)
مکمل گرافی r-منتظم گرافی \(\bar r\)-منتظم بوده و \(r + \bar r = p - 1\)
زیر گراف
گراف H را یک زیر گراف از G می گوییم هر گاه \(E(H) \subseteq E(G),V(H) \subseteq V(G)\)
برای مثال گراف G و سه زیر گراف آن را در زیر مشاهده می کنید:
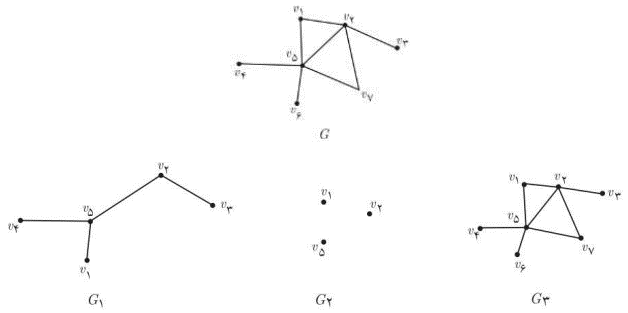
تهیه کننده: جابر عامری و الماسی کیا
مسیر در گراف
فصل 2 : گراف و مدل سازی
مسیر در گراف
فرض کنیم u و v دو راس از گراف G باشند. یک مسیر از u به v در G دنباله ای متشکل از راس های دو به دو متمایز است که از u شروع و به v ختم می شود به طوری که هر دو راس متوالی در این مسیر، مجاور هستند. طول مسیر همان تعداد یال های طی شده است که یکی کمتر از تعداد راس ها است.
قرارداد
هر راس به تنهایی، یک مسیر به طول صفر از خودش به خودش است.
گرافی که تنها از یک مسیر n راسی تشکیل شده باشد با \({P_n}\) نمایش می دهیم.
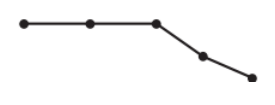
گراف های همبند
گراف G را همبند گوییم، هر گاه بین هر دو راس آن حداقل یک مسیر وجود داشته باشد، مانند گراف زیر:
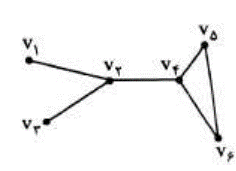
گرافی که همبند نباشد را ناهمبند می نامیم. مانند گراف های زیر:
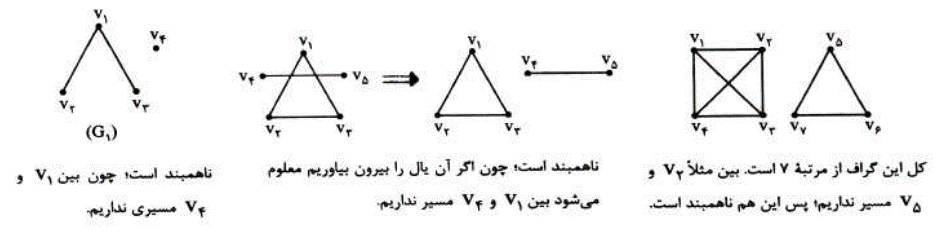
1 اگر \(q\langle p - 1\) باشد، گراف قطعا نا همبند است.
2 اگر \(q\rangle (\frac{{p - 1}}{2})\) باشد، گراف قطعا همبند است. همچنین اگر در گرافی \(\Delta = p - 1\) باشد (یعنی یک راس به همه وصل باشد) گراف قطعا همبند است.
دور در گراف
یک دور به طول m در گراف G دنباله ای از \(m + 1\) راس، که راس های متوالی مجاور بوده و m راس اول آن دو به دو متمایز بوده و راس آخر همان راس اول باشد. در شکل زیر دور \({v_1}{v_2}{v_3}{v_4}{v_1}\) را ببینید. این دور به طول 4 است.
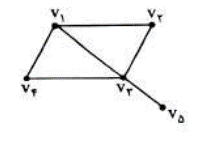
1 حداقل طول دور می تواند 3 باشد.
2 طول دور همان تعداد یال های طی شده است.
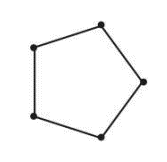
گرافی را که تنها از یک دور n راسی تشکیل شده باشد با \({C_n}\) نمایش می دهیم.
برای مثال \({C_5}\) را در شکل زیر می بینید:
تمرین
1 با توجه به گراف زیر یک مجموعه ی احاطه گر مینیمال بنویسید که مینیمم نباشد.
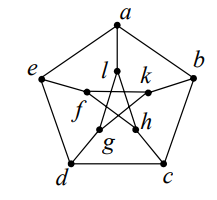
مجموعه ی \(\{ a,b,c,d,e\} \) احاطه گر مینیمال است ولی مینیمم نیست، مجموعه ی احاطه گر مینیمم این گراف \(\{ c,l,f\} \) می باشد.
2 درستی یا نادرستی گزاره های زیر را برسی کنید.
الف) مجموعه ی احاطه گر هر گراف، مساوی مجموعه ی احاطه گر مینیمم آن است.
نادرست
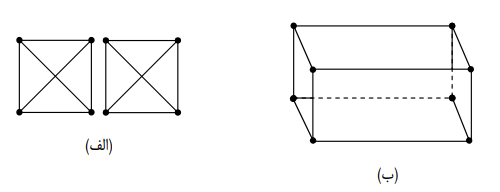
ب) مجموعه احاطه گر مینیمم هر دو گراف زیر یک مجموعه ی دو عضوی است.
درست
تهیه کننده: جابر عامری و الماسی کیا
مباحثی در ترکیبیات
فصل 3 : ترکیبیّات (شمارش)
مباحثی در ترکیبیات
اصل ضرب
اگر کاری در مرحله اول به m روش و در مرحله دوم به n روش و در مرحله سوم به P روش و ... انجام شود کل کار به \(m \times n \times P \times ...\) روش انجام می شود.
مثال
1 با حروف کلمه Stop چند کلمه چهار حرفی با تکرار حروف می توان نوشت در صورتی که:
الف) با حرف T شروع شود؟
\(1 \times 4 \times 4 \times 4 = 64\)
ب) با حرف P شروع شده و به حرف O ختم شود؟
\(1 \times 4 \times 4 \times 1 = 16\)
2 می خواهیم 5 توپ با شماره های \(1,2,3,4,5\) را در 3 جعبه به رنگ های آبی، زرد و قرمز توزیع کنیم. این کار به چند طریق امکان پذیر است؟
برای هر توپ 3 انتخاب وجود دارد؛ بنابراین طبق اصل ضرب \(3 \times 3 \times 3 \times 3 \times 3 = {3^5}\) است.
جایگشت
تعداد حالت های کنار هم قرار گرفتن n شی متمایز را جایگشت آن n شی متمایز نامیده و برابر است با: \(n!\)
مثال
5 دانش آموز به چند طریق می توانند در یک صف بایستند؟
\(5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\)
N نفر به چند طریق می توانند در یک صف بایستند به طوری که:
الف) k نفر مشخص همواره کنار هم باشند.
\((n - k + 1)! \times k!\)
ب) k نفر مشخص همواره کنار هم نباشند.
\(n! - (n - k + 1)! \times k!\)
مثال
به چند طریق می توان 7 دانش آموز را در یک صف قرار داد به طوری که:
الف) دو نفر از آنها که برادرند کنار هم باشند؟
\(\begin{array}{l}(n - k + 1)! \times k!\\(7 - 2 + 1)! \times 2! = 6! \times 2! = 720 \times 2 = 1440\end{array}\)
ب) دو نفر از آنها که برادرند کنار هم نباشند؟
\(\begin{array}{l}n! - (n - k + 1)! \times k!\\7! - (7 - 2 + 1)! \times 2! \to 7! - 6! \times 2! = 5040 - 1440 = 3600\end{array}\)
\(\begin{array}{l}0! = 1\\1! = 1\end{array}\)
جایگشت k شی از n شی متمایز
تعداد حالت های کنار هم قرار گرفتن k شی از n شی متمایز را با علامت \(P(n,k)\) نشان داده و از فرمول زیر حساب می کنیم:
\(P(n,k) = \frac{{n!}}{{(n - k)!}}\)
مثال
1 با حروف کلمه FAMILY و بدون تکرار حروف چند کلمه 4 حرفی شامل حرف M می توان ساخت؟
قرار دادن حرف M در یکی از چهار مکان به 4 طریق ممکن است و پر کردن سه مکان باقی مانده توسط 5 حرف باقی مانده به صورت زیر ممکن است:
\(P(5,3) = \frac{{5!}}{{(5 - 3)!}} = 60\)
طبق اصل ضرب = \(4 \times 60 = 240\)
2 شرکتی در نظر برای هر یک از شغل های نگهبانی، دفترداری، روابط عمومی و مسئول رایانه، یک نفر را استخدام کند، 10 نفر برای استخدام در این شغل ها داوطلب شده اند. شرکت به چند روش می تواند افراد را برای این مشاغل استخدام کند؟
برای نگهبانی هر کدام از 10 نفر را می توان انتخاب کرد پس 10 روش، برای دفترداری نیز 9 روش و برای روابط عمومی 8 روش و برای مسئول رایانه نیز 7 روش وجود دارد. در نتیجه \(10 \times 9 \times 8 \times 7\) طریق وجود دارد. (یا می توان ابتدا 4 نفر از 10 نفر را انتخاب کرده و سپس آن چهار نفر را برای شغل ها انتخاب نمود)
\(\left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right) \times 4! = \frac{{10!}}{{6!}}\)
ترکیب k شی از n شی متمایز
اگر از بین n شی متمایز بخواهیم k شی (\(k \le n\)) را انتخاب کنیم و حالت های کنار هم قرار گرفتن آنها اهمیتی نداشته باشد آن را یک ترکیب k شی از n شی می گوییم و با علامت \(C(n,k)\) یا \(\left( {\begin{array}{*{20}{c}}n\\k\end{array}} \right)\) نشان داده و از فرمول زیر محاسبه می کنیم:
\(C(n,k) = \frac{{n!}}{{k! \times (n - k)!}}\)
مثال
1 به چند طریق می توان از بین 8 نفر، یک تیم 3 نفری انتخاب کرد؟
\(C(8,3) = \frac{{8!}}{{3! \times 5!}} = 56\)
2 شرکتی در نظر برای هر یک از شغل های نگهبانی، دفترداری، روابط عمومی و مسئول رایانه، به ترتیب \(3,2,2,1\) را استخدام کند، 10 نفر برای استخدام در این شغل ها داوطلب شده اند. شرکت به چند روش می تواند افراد را برای این مشاغل استخدام کند؟
\(\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}7\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right)\)
جایگشت های با تکرار
اگر n شی متمایز داشته باشیم به طوری که P تای آنها از نوع اول، q تای آنها از نوع دوم و r تای آنها از نوع سوم و ... باشد تعداد کل جایگشت های اشیا برابر است با:
\(\frac{{n!}}{{p! \times q! \times r! \times ...}}\)
مثال
1 9 نفر به چند طریق می توانند در سه اتاق 2 نفره، 3 نفره و 4 نفره در یک هتل اسکان یابند؟
\(\begin{array}{l}\frac{{n!}}{{p! \times q! \times r! \times ...}}\\\frac{{9!}}{{2! \times 3! \times 4!}} = \frac{{362880}}{{288}} = 1260\end{array}\)
2 با حروف کلمات (انتخابات) چند کلمه 8 حرفی بدون توجه به مفهوم آن می توان ساخت؟
با توجه به اینکه 3 حرف (الف) و 2 حرف (ت) وجود دارد، در نتیجه \(\frac{{8!}}{{3! \times 2!}}\) است.
اگر یک شبکه \(n \times m\) مطابق شکل زیر داشته باشیم و فقط به راست یا بالا حرکت کنیم تعداد مسیر ها از A به B برابر است با:
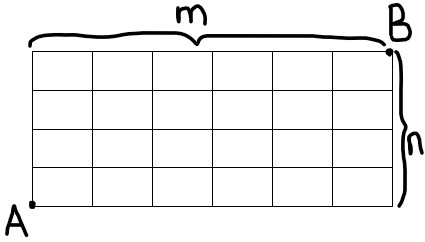
تعداد مسیر ها = \(\frac{{(n + m)!}}{{n! \times m!}}\)
مثال
چند مسیر از A به B وجود دارد به طوری که فقط مجاز باشیم به راست یا بالا جرکت کنیم؟

\(\begin{array}{l}\frac{{(n + m)!}}{{n! \times m!}}\\\frac{{(4 + 5)!}}{{4! \times 5!}} = \frac{{362880}}{{2880}} = 126\end{array}\)
حل معادله سیاله خطی با ضرایب واحد:
تعداد جواب های صحیح و نا منفی معادله \({x_1} + {x_2} + ... + {x_k} = n\) برابر است با:
\(\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right)\)
که همان تعداد انتخاب های دلخواه n شاخه گل از بین k نوع گل است.
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 7\) چند جواب صحیح و نا منفی دارد؟
n = 7
k = 3
\(\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{7 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9\\2\end{array}} \right) = \frac{{9!}}{{2! \times 7!}} = 36\)
2 به چند طریق می توان از بین 4 نوع گل، دسته گلی شامل 8 شاخه گل را به دلخواه انتخاب کرد؟
تعداد گل های نوع اول را \({x_1}\) و نوع دوم را \({x_2}\) و .... آنگاه در نظر می گیریم:
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 8\\n = 8,k = 4\\\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 + 4 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{11}\\3\end{array}} \right) = \frac{{11!}}{{3! \times 8!}} = 165\end{array}\)
تعداد جواب های طبیعی معادله \({x_1} + {x_2} + ... + {x_k} = n\) برابر است با:
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right)\)
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 5\) چند جواب صحیح و مثبت (طبیعی) دارد؟
n = 5
k = 3
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{5 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) = \frac{{4!}}{{2! \times 2!}} = 6\)
2 به چند طریق می توان دسته گلی شامل 9 شاخه گل را از بین 4 نوع گل انتخاب کرد به شرط آن که از هر نوع گل حداقل 1 شاخه انتخاب شود؟
چون از هر نوع گل حداقل 1 شاخه باید انتخاب شود و جواب های معادله عدد طبیعی هستند، آنگاه:
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 9\\n = 9,k = 4\\\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{9 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}8\\3\end{array}} \right) = 56\end{array}\)
حل معادله \({x_1} + {x_2} + ... + {x_k} = n\) به روش تغییر متغیر
اگر در مساله سیاله شرط هایی به صورت \({x_1} \ge a\) و \({x_2} \ge b\) و ... داشته باشیم در این صورت متغیر را تغییر داده و معادله را طبق شرایط زیر حل می کنیم:
\(\begin{array}{l}{x_1} \ge a \to {x_1} - a \ge 0 \to {x_1} - a = {y_1} \to {x_1} = {y_1} + a,{y_1} \ge 0\\{x_2} \ge b \to {x_2} - b \ge 0 \to {x_2} - b = {y_2} \to {x_2} = {y_2} + b,{y_2} \ge 0\end{array}\)
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 7\) چند جواب طبیعی دارد؟
\(\begin{array}{l}{x_1} \ge {x_1} = {y_1} + 1\\{x_2} \ge {x_2} = {y_2} + 1\\{x_3} \ge {x_3} = {y_3} + 1\\{y_1} + 1 + {y_2} + 1 + {y_3} + 1 = 7 \to {y_1} + {y_2} + {y_3} = 4\\n = 4,k = 3\\\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{4 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6\\2\end{array}} \right) = 15\end{array}\)
2 به چند طریق می توان 8 توپ یکسان را بین 4 نفر توزیع کرد، هرگاه بخواهیم هر نفر حداقل یک توپ داشته باشد؟
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 8,{x_i} \ge 1,i = 1,2,3,4\\n = 8,k = 4\\\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 35\end{array}\)
تمرین
1 با حروف کلمه (می سی سی پی) چند جایگشت 8 حرفی با معنا یا بی معنا می توان نوشت؟
تعداد (ی) = 4
تعداد (س) = 2
\(\frac{{8!}}{{4! \times 2!}} = 840\)
2 اگر داشته باشیم \(A = \{ 1,2,3,4\} \) و \(B = \{ 5,6,7,8,9\} \) در این صورت چند کد یا رمز 5 رقمی می توان نوشت که هر یک شامل دو رقم متمایز از A و سه رقم متمایز از B باشد؟
\(\left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) \times 5! = 7200\)
3 6 کتاب ریاضی مختلف و 5 کتاب فیزیک متمایز را به چند طریق می توان کنار هم در یک ردیف قرار داد به طوری که:
الف) کتاب ها یکی در میان قرار گیرند؟
\(6! \times 5!\)
ب) کتاب های ریاضی کنار هم و کتاب های فیزیک نیز کنار هم باشند؟
\(6! \times 5! \times 2!\)
4 به چند طریق می توان 4 خودکار متفاوت را بین 8 نفر توزیع کرد به شرطی که هیچکس بیشتر از یک خودکار نداشته باشد؟ (به هر نفر حداکثر یک خودکار داده باشیم)
\(P(8,4) = \frac{{8!}}{{(8 - 4)!}} = \frac{{8!}}{{4!}} = 1680\)
5 7 نفر به چند طریق می توانند در دو اتاق دو نفره و یک اتاق سه نفره قرار بگیرند؟
\(\frac{{7!}}{{2! \times 2! \times 3!}} = 210\)
6 به چند طریق می توان 5 توپ یکسان را بین 3 نفر و به دلخواه توزیع کرد؟
\(\begin{array}{l}\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right)\\{x_1} + {x_2} + {x_3} = 5 \to \left( {\begin{array}{*{20}{c}}{5 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 21\end{array}\)
7 به چند طریق می توان 8 توپ یکسان را بین 4 نفر توزیع کرد هر گاه بخواهیم هر نفر حداقل یک توپ داشته باشد؟
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 35\)
تهیه کننده: عادل نقدی
- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته
مربع های لاتین
فصل 3 : ترکیبیّات (شمارش)
مربع های لاتین
یک جدول مربعی از اعداد \(1,2,3,...,n\) به شکل یک مربع \(n \times n\) را که سطر ها و ستون های آن با اعداد \(1,2,3,...,n\) پر شده باشد و در هیچ سطر آن و نیز در هیچ ستون آن عدد تکراری وجود نداشته باشد، مربع لاتین می نامیم و به هر یک از اعداد درون مربع لاتین یک درایه می گوییم.
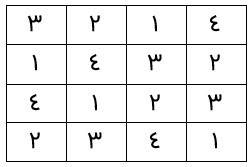
در حالت کلی شکل زیر یک مربع لاتین \(n \times n\) است که به آن مربع لایتن چرخشی می گوییم.

مربع لاتین از هر مرتبه ای وجود دارد.
یک مربع لاتین \(1 \times 1\) داریم:

ساخت مربع لاتین
روش چرخشی
در سطر اول اعداد \(1,2,3,...,n\) را می گذاریم، آخرین عدد سطر اول را که n است در ابتدای سطر دوم نوشته و بقیه عدد ها را در سطر دوم یکی یکی به راست می بریم و این کار را تکرار می کنیم.

کل مربع های لاتین مرتبه دو نوع هستند.
روی قطر اعداد تکراری
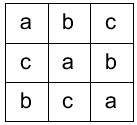
روی قطر اعداد غیر تکراری
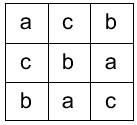
روش جا به جایی سطر و ستون
با تعویض جای هر دو سطر یا هر دو ستون یک مربع لاتین می توان مربع لاتین جدیدی ساخت.
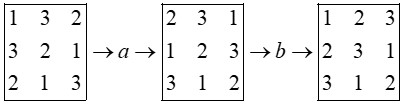
در a ستون 1 با ستون 3 تعویض شد و در b سطر 1 با سطر 2 تعویض شد.
روش جایگشت
می توانیم بدون تغییر جای سطر ها و ستون ها، جای خود عدد ها را با هم عوض کنیم، مثلا به جای تمام 3 ها 2 بنویسیم و برعکس یا همه 1 ها را 2 و همه 2 ها را به 3 و همه 3 ها را به 1 تبدیل کنیم و ... . در این صورت می گوییم جایگشت روی 1 عدد اعمال کرده ایم، با این روش مربع لاتین جدیدی ساخته می شود.
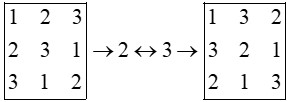
دو مربع لاتین متعامد
فرض کنیم A و B دو مربع لاتین هم مرتبه باشند به طوری که از کنار هم قرار دادن درایه های نظیر به نظیر این دو مربع، مربع جدیدی از همان مرتبه حاصل شود که هر خانه آن حاوی یک عدد دو رقمی است که تمام رقم های سمت چپ مربوط به مربع a و تمام رقم های سمت راست مربوط به مربع B (و یا برعکس) است، اگر هیچ یک از اعداد دو رقمی موجود در خانه های مربع جدید تکرار نشده باشند می گوییم دو مربع لاتین A و B متعامدند.
متعامد (عدد تکراری ندارد)
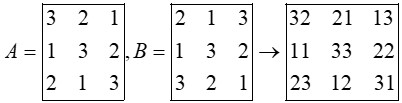
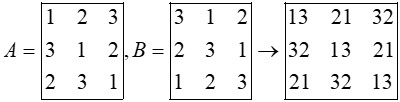
نا متعامد (عدد تکراری دارد)
مثال
دو مربع لاتین متعامد از مرتبه 3 بنویسید و متعامد بودن آنها را نشان دهید.
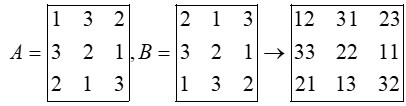
یک روش برای ساختن دو مربع لاتین متعامد از مرتبه یک عدد فرد:
به عنوان مثال نحوه ایجاد دو مربع لاتین متعامد \(3 \times 3\) (مرتبه فرد است) را توضیح می دهیم:
دو شکل مانند زیر ایجاد می کنیم:
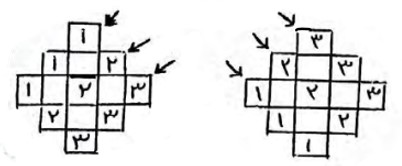
حال دو شکل را با هم ترکیب می کنیم:
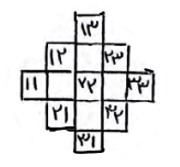
تهیه کننده: عادل نقدی
اصل شمول و عدم شمول
فصل 3 : ترکیبیّات (شمارش)
اصل شمول و عدم شمول
اصل شمول و عدم شمول برای دو مجموعه
تعداد عضو هایی که به مجموعه A یا به مجموعه B تعلق دارند برابر است با:
\(\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\)
واضح است که تعداد عضو هایی که به هیچ یک از مجموعه های A و B تعلق ندارند برابر است با:
\(\left| {\bar A\bar \cup \bar B} \right| = \left| {\bar A \cap \bar B} \right| = \left| {(A \cup B)'} \right| = \left| S \right| - \left| {A \cup B} \right|\)
تعداد اعداد طبیعی کوچکتر یا مساوی n که بر k بخش پذیرند برابر است با:
خارج قسمت تقسیم = \(\left[ {\frac{n}{k}} \right]\)
مثال
چند عضو از مجموعه \(S = \{ n \in \mathbb{N}|n \le 400\} \) نه بر 2 و نه بر 3 بخش پذیرند؟
\(\begin{array}{l}S = \{ 1,2,3,...,400\} \to \left| S \right| = 400\\ \div 2 = A \to \left| A \right| = \left[ {\frac{{400}}{2}} \right] = 200\\ \div 3 = B \to \left| B \right| = \left[ {\frac{{400}}{3}} \right] = 133\\ \div 3,2 = A \cap B \to \left| {A \cap B} \right| = \left[ {\frac{{400}}{{2 \times 3}}} \right] = \left[ {\frac{{400}}{6}} \right] = 66\\\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right| = 200 + 133 - 66 = 267\\\left| {(A \cup B)'} \right| = \left| S \right| - \left| {A \cup B} \right| = 400 - 267 = 133\end{array}\)
اصل شمول و عدم شمول برای سه مجموعه
تعداد عضو هایی که حداقل به یکی از سه مجموعه A یا B یا C تعلق دارد برابر است با:
\(\begin{array}{l}\left| {A \cup B \cup C} \right| = \left| A \right| + \left| B \right| + \left| C \right| - \left| {A \cap B} \right| - \left| {A \cap C} \right| - \left| {B \cap C} \right| + \left| {A \cap B \cap C} \right|\\\left| {{{\left( {A \cap B \cap C} \right)}^\prime }} \right| = \left| {A' \cap B' \cap C'} \right| = \left| S \right| - \left| {A \cup B \cup C} \right|\end{array}\)
مثال
چند عدد طبیعی مانند n به طوری که \(1 \le n \le 350\) وجود دارد که بر هیچ یک از اعداد 4 و 5 و 6 بخش پذیر نباشد؟
\(\begin{array}{l}\left| S \right| = 350,\left[ {4,5} \right] = 20,\left[ {4,6} \right] = 12,\left[ {5,6} \right] = 30,\left[ {4,5,6} \right] = 60\\\left| A \right| = \left[ {\frac{{350}}{4}} \right] = 87,\left| B \right| = \left[ {\frac{{350}}{5}} \right] = 70,\left| C \right| = \left[ {\frac{{350}}{6}} \right] = 58\\\left| {A \cap B} \right| = \left[ {\frac{{350}}{{20}}} \right] = 17,\left| {A \cap C} \right| = \left[ {\frac{{350}}{{12}}} \right] = 29,\left| {B \cap C} \right| = \left[ {\frac{{350}}{{30}}} \right] = 11\\\left| {A \cap B \cap C} \right| = \left[ {\frac{{350}}{{60}}} \right] = 5 \to \left| {A \cup B \cup C} \right| = 163 \to \left| {A' \cup B' \cup C'} \right| = 350 - 163 = 187\end{array}\)
تابع شماری
اگر A و B دو مجموعه باشند، تعداد توابع از A به B برابر است با:
\({\left| B \right|^{\left| A \right|}}\)
مثال
چند تابع از مجموعه \(A = \{ {a_1},{a_2},{a_3}\} \) به مجموعه \(B = \{ {b_1},{b_2}\} \) می توان نوشت؟
\(\left| A \right| = 3,\left| B \right| = 2 \to {\left| B \right|^{\left| A \right|}} = {2^3} = 8\)
اگر \(\left| A \right| = m\) و \(\left| B \right| = k\) با شرط \(m \le k\) تعداد توابع یک به یک از مجموعه A به مجموعه B برابر است با:
\({(k)_m} = \frac{{k!}}{{(k - m)!}}\)
مثال
به چند طریق می توان 4 خودکار متفاوت را بین 8 نفر توزیع کرد به شرط آن که هیچکس بیشتر از یک خودکار نداشته باشد؟ (به هر نفر حداکثر یک خودکار برسد)
تعداد حالت های ممکن \({\left( 8 \right)_4} = \frac{{8!}}{{4!}} = 1680\) که معادل است با پیدا کردن تعداد تابع های یک به یک از مجموعه ای 4 عضوی به مجموعه ای 8 عضوی
تابع f از مجموعه A به مجموعه B را پوشا می نامند هر گاه برد تابع f، شامل کل اعضای B باشد، به عبارت دیگر به هر عضو B یک پیکان رسم شود و آن را به صورت زیر نشان می دهند.
\(\begin{array}{l}A = \{ {a_1},{a_2},...,{a_n}\} ,B = \{ {b_1},{b_2},...,{b_n}\} \\f:A \to B\\{R_f} = B\end{array}\)
برای پیدا کردن تعداد تابع های پوشا از مجموعه n عضوی A به مجموعه m عضوی B از فرمول های زیر استفاده می کنیم که همان اصل شمول و عدم شمول است:
\(\begin{array}{l}{A_j} = \{ f:A \to B|f({a_i}) \ne {b_j},1 \le i \le n,1 \le j \le m\} \\\left| S \right| = {\left| B \right|^{\left| A \right|}} = {m^n},\left| {{A_1}} \right| = \left| {{A_2}} \right| = ... = \left| {{A_m}} \right| = {2^m}\\\left| {{A_1} \cap {A_2}} \right| = \left| {{A_1} \cap {A_3}} \right| = ... = \left| {{A_2} \cap {A_3}} \right| = ... = 1,\left| {{A_1} \cap {A_2} \cap {A_3} \cap ... \cap {A_m}} \right| = 0\\\left| {{{\bar A}_1} \cap {{\bar A}_2} \cap ... \cap {{\bar A}_m}} \right| = \left| {{{\bar A}_1}\bar \cup {{\bar A}_2}\bar \cup ...\bar \cup {{\bar A}_m}} \right| = \left| S \right| - \left| {{A_1} \cup {A_2} \cup ... \cup {A_m}} \right|\end{array}\)
مثال
با استفاده از اصل شمول و عدم شمول، تعداد توابع پوشا از یک مجموعه 4 عضوی به یک مجموعه 3 عضوی را بدست آورید.
\(\begin{array}{l}{A_j} = \{ f:A \to B|f({a_i}) \ne {b_j},1 \le i \le 4,1 \le j \le 3\} \\A = \{ {a_1},{a_2},{a_3},{a_4}\} ,B = \{ {b_1},{b_2},{b_3}\} \to \left| A \right| = 4,\left| B \right| = 3\\\left| S \right| = {3^4} = 81,\left| {{A_i}} \right| = {2^4} = 16 \to \left| {{A_i} \cap {A_j}} \right| = 1,\left| {{A_1} \cap {A_2} \cap {A_3}} \right| = 0\\\left| {{{\bar A}_1} \cup {{\bar A}_2} \cup {{\bar A}_3}} \right| = \left| S \right| - \left| {{A_1} \cup {A_2} \cup {A_3}} \right| = 81 - \left( {16 + 16 + 16 - 3 + 0} \right) = 36\end{array}\)
تعداد تابع های پوشا از مجموعه m عضوی A به مجموعه 3 عضوی B از فرمول زیر بدست می آید:
\(\begin{array}{l}\left| A \right| = m,\left| B \right| = 3\\f:A \to B,{R_f} = B\\{3^m} - (3 \times {2^m} - 3)\end{array}\)
مثال
تعداد تابع های پوشا از مجموعه 4 عضوی A به مجموعه 3 عضوی B چند تا است؟
\(\begin{array}{l}m = 4\\{3^4} - (3 \times {2^4} - 3) = 36\end{array}\)
تهیه کننده: عادل نقدی
اصل لانه کبوتری
فصل 3 : ترکیبیّات (شمارش)
اصل لانه کبوتری
اگر m کبوتر و n لانه داشته باشیم و \(m\rangle n\) و همه کبوتر ها درون لانه ها قرار بگیرند در این صورت لانه ای وجود دارد که حداقل دو کبوتر در آن قرار گرفته است.
مثال
در کلاس 40 نفره، حداقل چند نفر ماه تولدشان یکسان است؟
40 نفر را کبوتر و 12 ماه سال را لانه در نظر می گیریم \(40 \div 12 = 3 \to 3 \times 12 = 36 \to 40 - 36 = 4\) باقی مانده صفر نشد پس حداقل \(3 + 1\) یعنی 4 نفر می توان یافت.
اگر باقی مانده صفر نشود یک واحد به خارج قسمت اضافه می کنیم.
تعمیم اصل لانه کبوتری
هر گاه (\(kn + 1\)) کبوتر یا بیشتر در n لانه قرار بگیرند در این صورت لانه ای وجود دارد که حداقل (\(k + 1\)) کبوتر در آن قرار گرفته است.
مثال
1 در یک اردوی دانش آموزی حداقل چند دانش آموز وجود داشته باشند تا اطمینان داشته باشیم که حداقل 7 نفر از آنها ماه تولد یکسانی دارند؟
\(\begin{array}{l}k + 1 = 7 \to k = 6\\kn + 1 = \left( {6 \times 12} \right) + 1 = 73\end{array}\)
2 در یک دبیرستان حداقل چند دانش آموز وجود داشته باشد تا مطمئن باشیم حداقل 10 نفر از آنها ماه و روز هفته تولدشان یکی است؟
\(\begin{array}{l}year = 12month\\week = 7day\\ \to n = 12 \times 7 = 84\\k + 1 = 10 \to k = 9 \to kn + 1 = 9 \times 84 + 1 = 757\end{array}\)
تمرین
1 54 شاخه گل را حداکثر در چند گلدان قرار دهیم تا اطمینان داشته باشیم گلدانی هست که در آن حداقل 5 شاخه گل قرار گرفته است؟
\(\begin{array}{l}k + 1 = 5 \to k = 4\\kn + 1 = 54 \to 4n + 1 = 54 \to n = \left[ {\frac{{53}}{4}} \right] = 13\end{array}\)
پس n باید حداکثر 13 باشد.
2 در بین اعداد 1 تا 90 چند عدد وجود دارد که بر 2 یا 3 بخش پذیر باشند؟
\(\begin{array}{l}\left| A \right| = \left[ {\frac{{90}}{2}} \right] = 45\\\left| B \right| = \left[ {\frac{{90}}{3}} \right] = 30\\\left| {A \cap B} \right| = \left[ {\frac{{90}}{6}} \right] = 15\\\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right| = 45 + 30 - 15 = 60\end{array}\)
3 در یک اردوی دانش آموزی حداقل چند دانش آموز حضور داشته باشند تا اطمینان داشته باشیم که لااقل 7 نفر از آنها ماه تولد یکسانی دارند؟
\(\begin{array}{l}k + 1 = 7 \to k = 6\\n = 12\\kn + 1 = \left( {6 \times 12} \right) + 1 = 73\end{array}\)
4 چند عدد طبیعی مانند n به طوریکه \(1 \le n \le 350\) وجود دارد که بر هیچ یک از اعداد 4 و 6 بخش پذیر نباشد؟
\(\begin{array}{l}\left| {\bar A \cap \bar B} \right| = \left| {\bar A \cap \bar B} \right| = \left| S \right| - \left( {\left| A \right| + \left| B \right| - \left| {A \cap B} \right|} \right) = 350\\350 - \left( {\left[ {\frac{{350}}{4}} \right] + \left[ {\frac{{350}}{6}} \right] - \left[ {\frac{{350}}{{12}}} \right]} \right) = 234\end{array}\)
تهیه کننده: عادل نقدی
- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته



1736019749.png)















