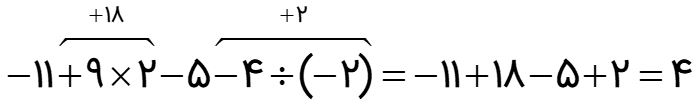آیا درسنامه ریاضی هفتم، مطابق با آخرین تغییرات کتب درسی است ؟

بله، درسنامه ریاضی هفتم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 تدوین شده است.

آیا نکات درس به صورت کامل بیان شده اند ؟

بله، تمام نکات به صورت کاملا شیوا و با هدف یادگیری و تسلط به مبحث بیان شده اند.

درسنامه کامل ریاضی هفتم

تعداد بازدید : 301.01k

خلاصه نکات ریاضی هفتم - درسنامه شب امتحان ریاضی هفتم - جزوه شب امتحان ریاضی هفتم نوبت اول

راهبردهای حل مسئله

فصل 1 : راهبردهای حل مسئله

مراحل حل یک مسئله

برای حل یک مسئله بایستی دو روش زیر را به کار ببریم:

1) فهمیدن مسئله

2) انتخاب راهبرد مناسب

1- فهمیدن مسئله

یعنی ارتباطی بین اطلاعات داده شده در مسئله و خواسته های آن پیدا کرده و آن ها را به خوبی درک کنیم. برای فهمیدن یک مسئله می توانیم کارهایی که در زیر آمده است را دنبال کنیم:

1) اطلاعات داده شده در مسئله را مشخص کنیم.

2) خواسته های مسئله را نیز مشخص کنیم.

3) مسئله را به صورت خلاصه شده بیان کنیم.

4) مسئله را با زبان و بیان خود توضیح دهیم.

5) مسئله را نمایش دهیم.

6) از شکل ها و اشیا برای مدل سازی در حل مسئله استفاده کنیم.

2- انتخاب راهبرد مناسب

انتخاب راهبرد مناسب یعنی یک روش یا راه حل مناسب برای حل مسئله یافته و با مرور راهبردها، تشخیص دهیم که کدام یک برای حل مسئله مناسب می باشد.

راهبردهای حل مسئله

1- راهبرد رسم شکل

۲- راهبرد الگوسازی (تفکّر نظام دار)

3- راهبرد حذف حالت های نامطلوب

4- راهبرد الگویابی

5- راهبرد حدس و آزمایش

6- راهبرد زیر مسئله

۷- راهبرد حل مسئله ساده تر

۸- راهبرد روش های نمادین

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد الگوسازی (تفکّر نظام دار)

فصل 1 : راهبردهای حل مسئله

راهبرد الگوسازی

برای حل بعضی از مسئله ها باید همه حالت های ممکن را بنویسید. برای اینکه هیچ حالتی از قلم نیفتد، لازم است آنها را با نظم، الگو و ترتیبی مشخص بنویسید. الگوسازی به شما کمک می کند تا مطمئن شوید همه حالت ها را نوشته اید. بنابراین در مسئله هایی که لازم است همه جواب ها و پاسخ های ممکن را بنویسید، می توانید از این راهبرد استفاده کنید. با توجه به نظم و ترتیبی که می سازید به این راهبرد تفکر نظام دار نیز می گویند.

دو عدد طبیعی پیدا کنید که حاصل ضرب آنها ۲۴ و حاصل جمع آنها کمترین مقدار باشد. جدول را با یک نظم و ترتیب کامل کنید.

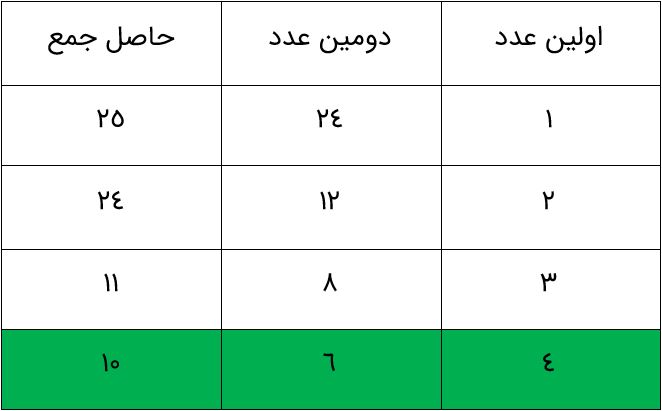
جواب سطر رنگی می باشد.

مجموع دو عدد طبیعی 24 است. حداکثر حاصل ضرب آن ها کدام است؟

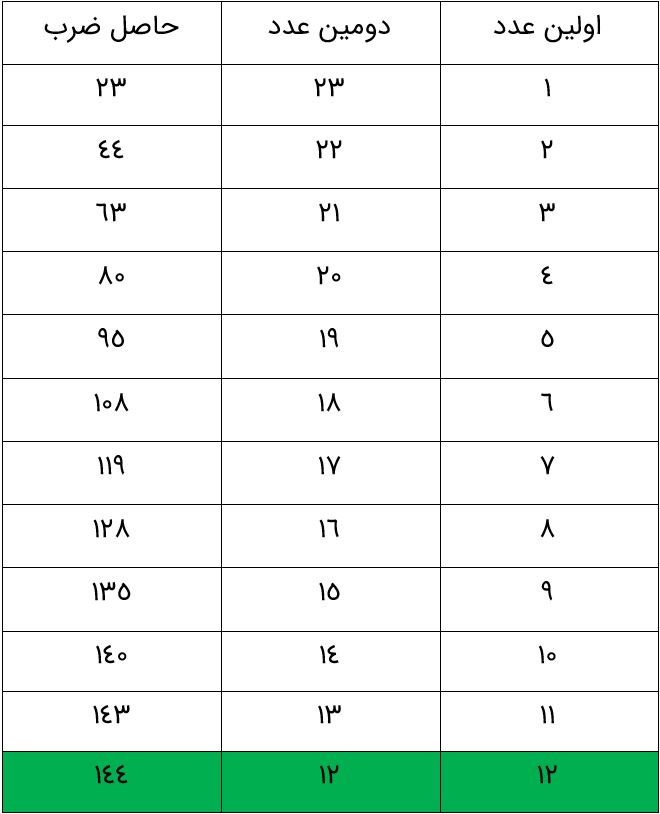
بیشترین مقدار حاصل ضرب عدد 144 می باشد.

با رقم های 6، 7 و 9 چند عدد دو رقمی بدون تکرار رقم های می توان نوشت؟

باید سعی کنیم همه حالت های ممکن را بیابیم:

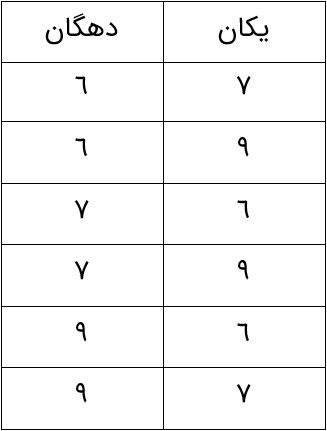
6 عدد دو رقمی بدون تکرار رقم ها می توان نوشت. دقت کنید که ابتدا دهگان را ثابت گرفتبم و حالت ها را نوشتیم.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

راهبرد حذف حالت های نامطلوب

فصل 1 : راهبردهای حل مسئله

راهبرد حذف حالت های نامطلوب

به شرایط و اطّلاعات مسئله توجه کنید و حالت های نامطلوب و نادرست را کنار بگذارید. آنگاه پاسخ مسئله یا همان حالت های مطلوب به دست می آیند. برای پیدا کردن تمام حالت های ممکن می توانید از راهبرد الگوسازی استفاده کنید . ابتدا فهرستی از تمام حالت ها به دست آورید؛ سپس با توجه به شرایط گفته شده در مسئله، حالت های نامطلوب را حذف کنید.

مجموع سن سه نفر ۱۴ سال و حاصل ضرب سن آنها ۷۰ است. سن بزرگ ترین نفر چقدر است؟

سن بزرگ ترین نفر 7 سال می باشد.

مجموع ۳ عدد متفاوت ۱۱ و حاصل ضرب آن‌ها ۳۶ شده است. این اعداد را مشخص کنید.

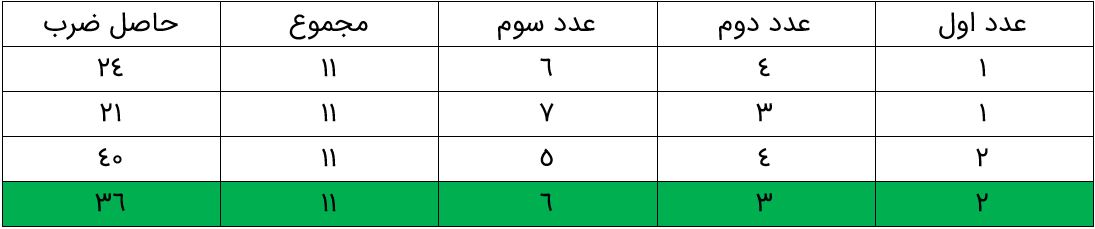
این اعداد به ترتیب 2، 3 و 6 می باشند.

مجموع سن دو نفر ۲۰ سال و حاصل ضرب سن آن‌ها ۹۶ است. اختلاف سن آن‌ها را بیابید.

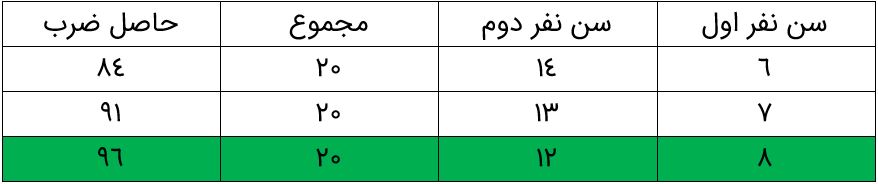
راهبرد الگویابی

فصل 1 : راهبردهای حل مسئله

راهبرد الگویابی

در ریاضی با دو نوع الگوی عددی یا هندسی رو به رو می شویم. کشف الگو، رابطه و نظم موجود در بین دنباله های عددی یا هندسی کمک می کند تا بتوانید خواسته مسئله را به دست آورید. این راهبرد در مسئله هایی کاربرد دارد که بین شکل ها یا عددها، الگو و رابطه خاصی وجود داشته باشد.

سه عدد بعدی الگوی زیر را بنویسید رابطه بین عددها را توضیح دهید.

\(1\;,\;4\;,\;9\;,\;16\;,\;\;\;,\;\;\;,\;\)

جواب:

اگر با دقت به اعداد این الگو توجه کنیم متوجه می شویم که همگی آنها مجذور شده اند ( به توان ۲ رسیده اند). پس مجذورهای بعدی را به سادگی می نویسیم:

\(1\;,\;4\;,\;9\;,\;16\;,\;25\;,\;36\;,\;49\)

به شکل زیر نگاه کنید. شکل دهم چند دایره خواهد داشت؟

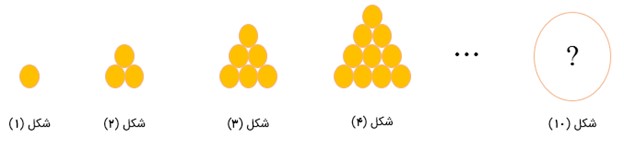
1 : شکل (1)

3 = 2 + 1 : شکل (2)

6 = 3 + 2 + 1 : شکل (3)

10 = 4 + 3 + 2 + 1 : شکل (4)

55 = 10 + 9 + ... + 4 + 3 + 2 + 1 : شکل (10)

حاصل عبارت زیر را بدست آورید.

\(\frac{{12}}{{13}} \times \frac{{13}}{{14}} \times \frac{{14}}{{15}} \times \cdots \times \frac{{112}}{{113}} = \)

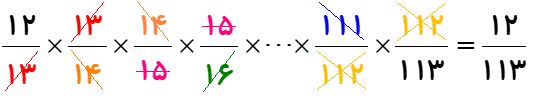
مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد حدس و آزمایش

فصل 1 : راهبردهای حل مسئله

راهبرد حدس و آزمایش

ممکن است حلّ یک مسئله، روش و راه حل مستقیمی نداشته باشد یا راه رسیدن به جواب آن طولانی و دشوار باشد. شما می توانید با یک روش منطقی و منظم پاسخ احتمالی مسئله را حدس بزنید؛ سپس با توجه به شرایط گفته شده در مسئله، حدس خود را بررسی کنید و با توجه به نتیجه به دست آمده حدس بعدی را بزنید تا کم کم به پاسخ مسئله نزدیک شوید. برای نشان دادن حدس ها و آزمایش های خود راه حل مناسبی پیدا کنید.

۲۰ دستگاه دوچرخه و سه چرخه در یک پارکینگ وجود دارد. اگر تعداد کل چرخ های آنها ۴۵ عدد باشد، چند دوچرخه و چند سه چرخه در پارکینگ وجود دارد؟

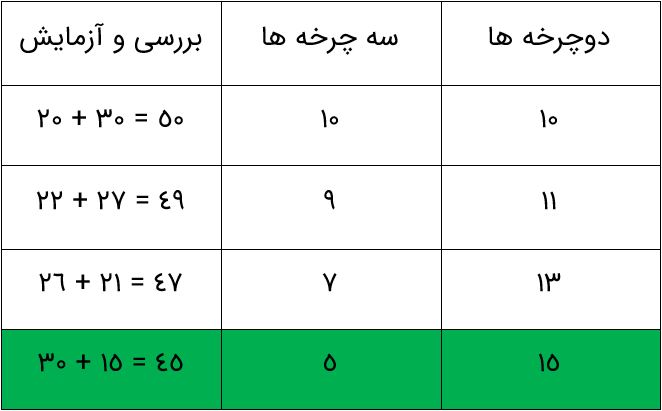
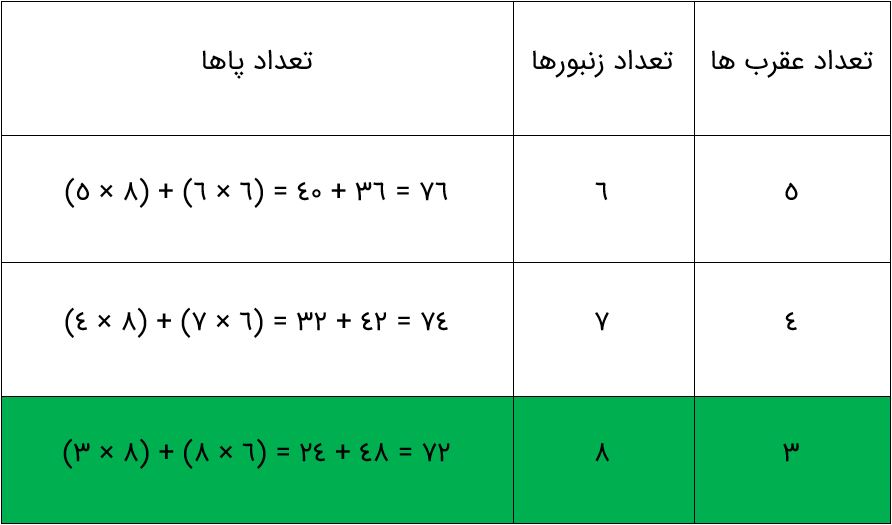
در یک ظرف شیشه ای تعدادی زنبور و عقرب انداخته ایم. اگر تعداد سرها 11 تا و مجموع پاهای آن ها 72 باشد، چند زنبور و چند عقرب در ظرف وجود دارد؟ (راهنمایی: عقرب ها 8 پا و زنبورها 6 پا دارند)

در جای خالی، عدد مناسب قرار دهید:

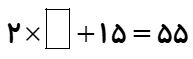\(% MathType!Translator!2!1!AMS LaTeX.tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbjjvqon % vyUnharmWu51MyVXgaruavP1wzZbItLDhis9wBH5gatCvAUfKCHjwA % Jbqegieil92BKf2Aaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaG % qiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0x % bba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adba % qaaeGaciGaaiaadeabauaadaGbaaGcbaGaeGOmaiJaey41aq7aauIh % aeaaaaGaey4kaSIaeGymaeJaeGynauJaeyypa0JaeGynauJaeGynau % daaa!483B! \[2 \times \boxed{} + 15 = 55\]% MathType!End!2!1! \)

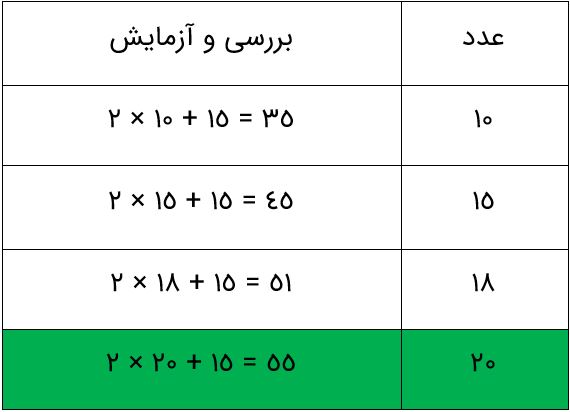
عدد مناسب جای خالی، 20 می باشد.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

راهبرد زیر مسئله

فصل 1 : راهبردهای حل مسئله

راهبرد زیرمسئله

مسئله پیچیده و چند مرحله ای را به چند مسئله ساده تبدیل کنید. فهرستی از این زیر مسئله ها را درست کنید؛ سپس به ترتیب به آنها پاسخ دهید. اگر ترتیب زیر مسئله ها را درست تشخیص داده باشید، حل هر زیر مسئله به حل مسئله بعدی کمک می کند تا در نهایت به خواسته اصلی مسئله برسید.

پس انداز هفتگی محمد ۳۰۰۰ تومان است. او حساب کرد ۵ هفته پس انداز او نصف قیمت کیفی است که دوست دارد بخرد.

الف) پس انداز ۵ هفته چقدر می شود؟

ب) اگر این عدد نصف قیمت کیف باشد قیمت کیف چقدر است؟

الف)

\(3000\; \times \;5 = 15000\)

ب)

\(15000\; \times \;2 = 30000\)

خمس نصف عددی 5 است. دو برابر این عدد چند است؟

به فرض مسئله توجه کنید:

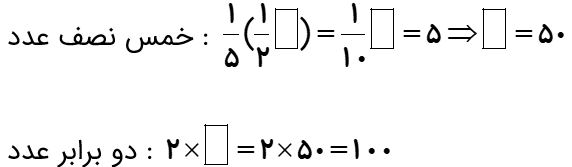
فروشنده ای به ازای هر کیلوگرم سیب 30% و به ازای هر کیلوگرم خیار 20% سود می کند. اگر این فروشنده 15 کیلوگرم سیب 5000 تومانی و 20 کیلوگرم خیار 4000 تومانی بفروشد، در مجموع چند تومان سود کرده است؟

تومان \(\frac{{30}}{{100}} \times 5000 \times 15 = 22500\) :سود حاصل از فروش سیب ها

تومان \(\frac{{20}}{{100}} \times 4000 \times 20 = 16000\) :سود حاصل از فروش خیار ها

تومان \(22500 + 16000 = 38500\) :سود کل <=

راهبرد حل مسئله ساده تر

فصل 1 : راهبردهای حل مسئله

راهبرد حل مسئله ساده تر

برای حل بعضی از مسئله ها، ابتدا مسئله ای ساده تر را که با مسئله اصلی در ارتباط است، حل می کنیم. سپس با استفاده از نتیجه و پاسخ مسئله ساده شده، جواب مسئله اصلی را به دست می آوریم. برای ساده کردن مسئله می توان از عددهای تقریبی یا عددهای کوچک تر استفاده کرد. برای نتیجه گیری و پیدا کردن پاسخ مسئله اصلی، از راهبرد الگویابی استفاده می کنیم و الگوی کشف شده در مسئله ساده را به مسئله اصلی مرتبط می کنیم.

قطر خورشید ۱۳۹۲۵۳۰ کیلومتر و قطر کره زمین 12756/6 کیلومتر است. قطر خورشید تقریباً چند برابر قطر زمین است؟

برای ساده شدن مسئله بهتر است از عددهای تقریبی استفاده کنید. خلاصه مسئله ساده شده را بنویسید و پاسخ دهید:

\(\begin{array}{l}1,392,530 \simeq 1,000,000\\\\12,756/6 \simeq 10,000\\\\1,000,000 \div 10,000 = 100\\\\1392530 \div 12,756/6 \simeq 100\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد روش های نمادین

فصل 1 : راهبردهای حل مسئله

راهبرد روش های نمادین

بسیاری از مسئله ها را می توانیم به کمک نمادهای جبری به یک معادله تبدیل کنیم. از فصل سوم به بعد می توانید از این راهبرد نیز برای حل مسئله استفاده کنید. در بعضی از مسئله ها هم می توانیم از مدل سازی هندسی استفاده کنیم. تبدیل مسئله به یک شکل هندسی و حل هندسی آن نیز نوعی روش نمادین یا مدل سازی به شمار می رود.

احمد ۳۰۰۰۰ تومان پول داشت. او ۴ دفتر خرید و ۲۰۰۰ تومان برایش باقی ماند. قیمت هر دفتر چقدر است؟

متن این سؤال را می توانید با تساوی زیر نشان دهید:

که مربع نشان دهنده تعداد دفترهاست.

اکنون می توانید عددی را که باید در مربع قرار گیرد حدس بزنید و آزمایش کنید.

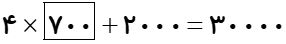
در یک کاری، جریمه عقب افتادگی کار دو برابر جریمه عقب افتادگی قبلی است. اگر یک کارگر پس از 3 بار عقب افتادگی در مجموع 210000 تومان جریمه شود، جریمه عقب افتادگی اول او چقدر بوده است؟

در این سوال هر جریمه عقب افتادگی دو برابر جریمه عقب افتادگی قبلی است:

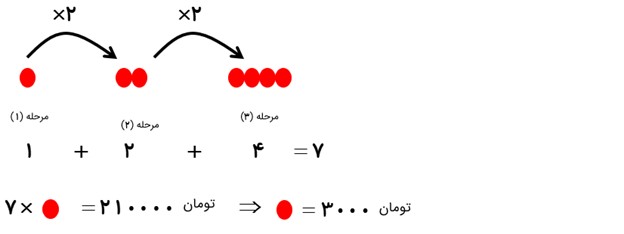
ثلث پول حسین با چهار برابر پول رضا برابر است. اگر آنها در مجموع 26000 تومان پول داشته باشند، پول حسین چند تومان است؟

با دو مجهول سر و کار داریم. با استفاده از نمادهای زیر، مسئله را حل می نماییم:

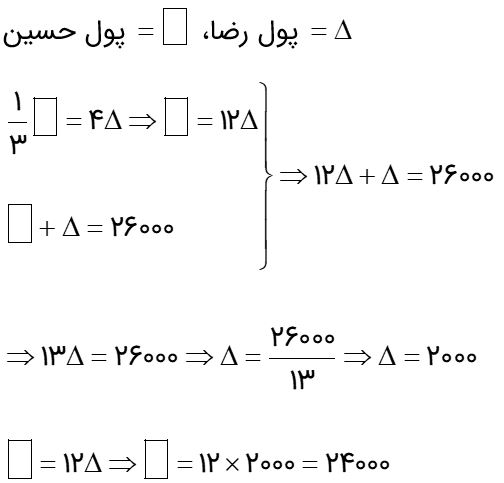
تومان 2000 = پول رضا، تومان 24000 = پول حسین

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

راهبرد رسم شکل

فصل 1 : راهبردهای حل مسئله

راهبرد رسم شکل

کشیدن یک شکل مناسب می تواند به حل مسئله کمک کند یا به طور کامل آن را حل کند؛ به طوری که نیازی به نوشتن عملیات و محاسبه نباشد. گاهی ممکن است شکل را فقط تصور کنید و آن را رسم نکنید. منظور از رسم شکل، نقاشی نیست، بلکه می توانید برای این کار شکل های ساده بکشید.

مثال

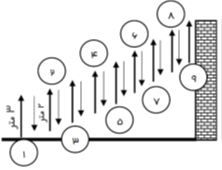
قورباغه ای می خواهد از یک دیوار عمودی بالا برود. او با هر جهش ۳ متر بالا می رود و هر بار ۲ سر می خورد و پایین می آید. اگر ارتفاع دیوار ۹ متر باشد ، او با چند جهش به بالای دیوار می رسد؟

همانطور که در شکل پیداست با نهمین پرش به بالای دیوار می رسد.

مثال

توپی از ارتفاع 32 متری سطح زمین رها می شود و پس از هر بار برخورد با زمین نصف ارتفاع قبلی خود را بالا می آید. این توپ از لحظه رها شدن تا سومین مرتبه که به زمین می خورد، چند متر حرکت کرده است؟

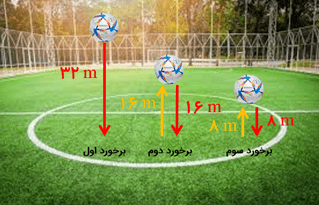
\(32 + 16 + 16 + 8 + 8 = 80\,m\)

یک استخر مستطیل شکلی به طول 6 متر و عرض 4 متر در باغچه ای وجود دارد. می خواهیم به فاصله یک متر از لبه های استخر را دور تا دور آن حفاظ بکشیم. به چند متر از این حفاظ نیاز داریم؟

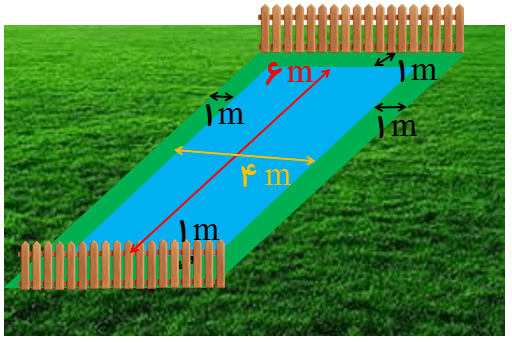
دور تا دور (محیط مستطیل)

2 × (عرض + مستطیل) = محیط مستطیل

8 = 2 + 6 = طول مستطیل

6 = 2 + 4 = عرض مستطیل

متر 28 = 2 × (6 + 8)

عددهای علامت دار

فصل 2 : عددهای صحیح

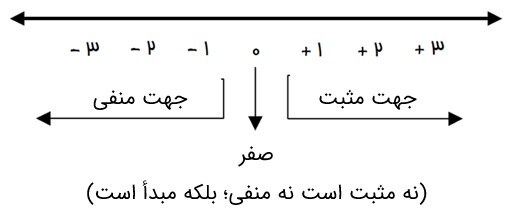
در ریاضیات برای ساده و مختصر کردن بیان عددهای علامت دار از علامت های + و - استفاده می کنیم. برای تعیین علامت عددها نیاز داریم که محل مبدأ و واحد اندازه گیری و همچنین جهت های مثبت و منفی را قرارداد کنیم و براساس آن، عددها را علامت دار کنیم.

برای یکی شدن قراردادها، سمت راست را روی محور مثبت و سمت چپ را منفی در نظر می گیرند.

هر یک از عددهای … را عددهای صحیح می نامیم. «عدد صفر نه مثبت است و نه منفی.»

هرچه به سمت مثبت پیش می رویم عددها بزرگتر می شوند. بنابراین می توان نوشت: ۱ + > ۱ -

چند تا از عددهای مجموعه مقابل صحیح اند؟

\(\left\{ { - \frac{{2/4}}{6}\,,\, - 2\frac{4}{2}\,,\,\frac{5}{4}\,,\,0\,,\, - \frac{{1071}}{9}} \right\}\)

عددهای \(\left\{ { - 2\frac{4}{2},\,0\,,\, - \frac{{1071}}{9}} \right\}\) عددهای صحیح هستند.

بین 5- و 9+ چند عدد صحیح وجود دارد؟

تعداد عددهای صحیح بین دو عدد m و n که n>m برابر است با: 1 - m - n ؛ بنابراین:

13 = 1 – (5 + 9) = 1 – ((5–) – 9+)

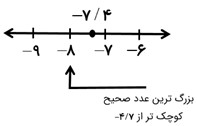
بزرگترین عدد صحیح کوجک تر از 7/4- کدام است؟

بزرگ ترین عدد صحیح کوچک تر از 7/4- عدد 8- است. همچنین می توان از محور اعداد نیز استفاده کرد:

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

قرینه اعداد صحیح

فصل 2 : عددهای صحیح

قرينه هر عدد منفی، عددی مثبت و قرینه هر عدد مثبت، عددی منفی است. قرينه صفر هم خود صفر است. برای نمایش قرینه هر عدد از نماد ( - ) در سمت چپ آن عدد استفاده می کنیم.

8- = (8+)- = قرینه (8+)

5+ = (5-)- = قرینه (5-)

قرينه هر عدد صحیح را می توان با تغییر علامت آن عدد به دست آورد .

قرينه ی قرينه هر عدد صحيح، مساوی خودش است.

\(\begin{array}{l} - \left[ { - \,( - \,3)} \right] = - \,3\\\\ - \left[ { + \,( - \,6)} \right] = + \,6\end{array}\)

عددهای صحیح مثبت، همان عددهای طبیعی اند؛ برای مثال می توان نوشت:

\( + \,3 = 3\;\;\;\;\;,\;\;\;\;\; + 6 = 6\)

عددهای صحیح شامل عددهای صحیح مثبت ، صفر و عددهای صحیح منفی می شوند.

جمع هر عدد صحيح با قرینه اش برابر صفر می شود.

\(7\, - \,7 = 7 + \,(\, - \,7) = 0\)

جمع هر عدد صحیح با صفر برابر خودش می شود.

\(( - \,9) + 0 = - \,9\;\;\;\;\;\;,\;\;\;\;\;\;4 + 0 = 4\)

هر عدد صحیح مثبت از هر عدد صحیح منفی بزرگتر است.

همه عددهای صحیح مثبت از صفر بزرگ ترند.

همه عددهای صحیح منفی از صفر کوچکتر هستند.

قرینه عدد صفر نسبت به 2- کدام است؟

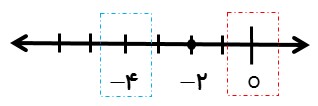
عدد قرینه 0 نسبت به 2- : \( \circ - ( - 2) = 2 \Rightarrow \,\, - 2 - (2) = - 4\)

قرینه قرینه قرینه عدد 10 کدام است؟

هر کلمه قرینه را با نماد – نشان می دهیم:

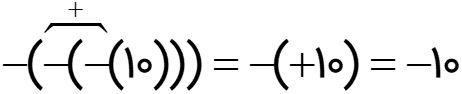
اگر عدد 25- را 1023 بار قرینه کنیم، نتیجه حاصل چه عددی می شود؟

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

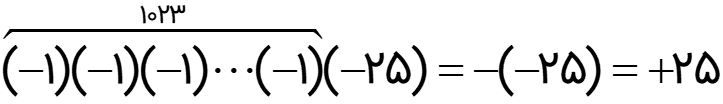
حرکت روی محور عددهای صحیح

فصل 2 : عددهای صحیح

شامل دو بخش زیر است:

الف) جهت:

حرکت به سمت راست مثبت +، حرکت به سمت چپ -، در جای خود حرکت 0 (صفر).

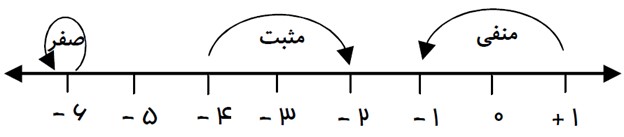
ب) اندازه:

به مقدار جابجایی که با عدد نشان داده می شود.

اگر متحرکی فاصله 4- تا 6+ را در 20 ثانیه طی کند، فاصله 5- تا 20- را در چند ثانیه طی هواهد کرد؟

منظور از فاصله، مسافت طی شده توسط متحرک است که برابر است با:

عدد مبدأ – عدد مقصد = فاصله

10+ = (4–) – 6+ : فاصله 4– تا 6+

15– = (5–) – (20–) : فاصله 5– تا 20–

10+ یعنی 10 واحد جلو رفته و 15– یعنی 15 واحد به عقب برگشته است:

ثانیه \(?\,\, = \,\frac{{20 \times 15}}{{10}} = 30\)

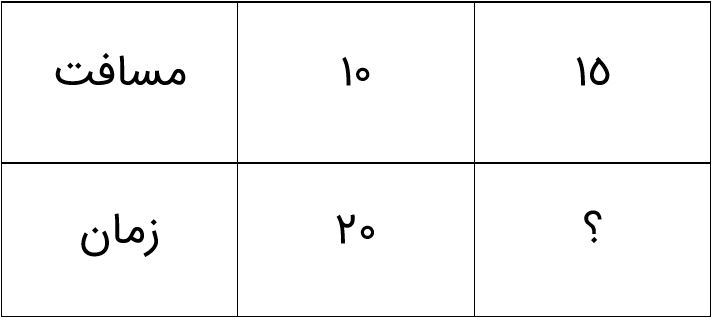
بردار 5- ابتدا در 1- را رسم کنید.

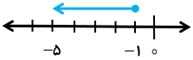
از نقطه 10+ برداری را که انتهای آن نقطه 3+ است، رسم می کنیم. اگر انتهای بردار را به 1+ منتقل کنیم، باید بردار را از چه نقطه ای رسم کنیم؟

ابتدا خود بردار (اندازه و جهت) را به دست می آوریم:

\(\,\, = ( + 3) - ( + 10) = - 7\) اندازه بردار <= ابتدا – انتها = اندازه بردار

سپس انتهای بردار را جا به جا می کنیم و ابتدای بردار جدید را به دست می آوریم:

<= ابتدا – انتها = بردار \( - 7 = + 1 - \)ابتدا

ابتدا – \( = - 7 - 1 = - 8\)

\( = 8\)ابتدا

جمع عددهای صحیح روی محور

فصل 2 : عددهای صحیح

اگر دو یا چند حرکت روی محور پشت سر هم انجام گیرد، می توان برای این حرکات یک تساوی جمع نوشت:

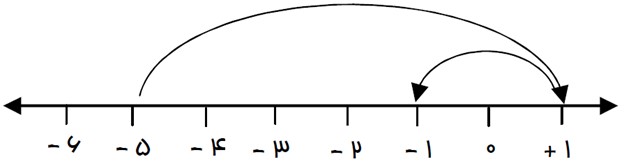
\(( + \,6) + ( - \,2) = ( + \,4)\)

مثال

جمع متناظر نمودار زیر را بنویسید و بدست آورید.

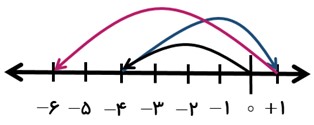
جمع متناظر نمودار بالا به صورت زیر است:

\(( - 4) + ( + 5) + ( - 7) = - 6\)

برای جمع زیر نمودار متناظر را نوشته و جواب را بدست آورید.

\(( + \,6) + ( - \,2) + ( - 3) = \)

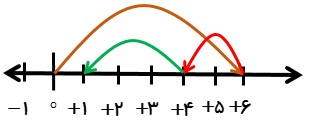
\(( + \,6) + ( - \,2) + ( - 3) = + 1\)

جمع و تفریق عددهای صحیح (بدون محور):

باید گام های زیر را به ترتیب انجام داد:

گام اول، مختصر یا ساده نویسی:

پرانتزها را حذف کنید.

گام دوم، تعیین علامت:

اگر قبل از عددی بیش از یک علامت وجود داشت ، باید به کمک عمل ضرب آنها را به یک علامت تبدیل کنید.

\(\begin{array}{l} - \,( - \,7) = + \,7\\\\ + \,( - \,2) = - \,2\end{array}\)

برای این کار از جدول داده شده کمک بگیرید:

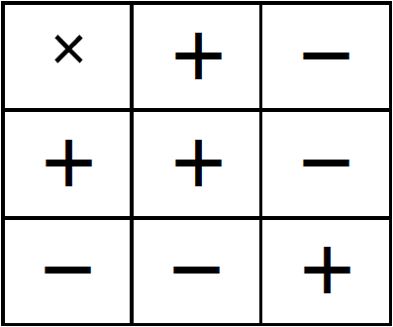
گام سوم، تعیین علامت حاصل:

پس از مختصر نویسی و تعیین علامت عددهای صحیح نوبت به یافتن علامت جواب (حاصل) می باشد. اگر هر دو علامت یک جور بود ، یک علامت را برای جواب قرار داده و عددها را جمع می کنیم:

\(\begin{array}{l}8 - \,( + \,7) = 8\, - \,7 = + \,1\\\\( - \,12) + \,( - \,7) = - \,12\, - \,7 = - \,19\end{array}\)

اگر علامت ها یک جور نبود، علامت عدد ظاهراً بزرگتر را برای جواب قرار داده و عددها را از هم کم می کنیم:

\(\begin{array}{l}8 - \,( - \,7) = 8\, + \,7 = + \,15\\\\( - \,18) + \,( + \,11) = - \,18\, + \,11 = - \,7\end{array}\)

مثال

حاصل عبارت \(( - 1) - ( - 2) - ( - 3) - ( - 4) - ( - 5)\) را بدست آورید.

\(\begin{array}{l}( - 1) - ( - 2) - ( - 3) - ( - 4) - ( - 5) = \\\\( - 1) + 2 + 3 + 4 + 5 = 13\end{array}\)

قرینه حاصل عبارت \( - \left[ {\left( { + 14} \right) - \left( { - 2} \right) - \left( {10} \right) + \left( { - 4} \right)} \right]\) را بدست آورید.

\(\begin{array}{l} - \left[ {\left( { + 14} \right) - \left( { - 2} \right) - \left( {10} \right) + \left( { - 4} \right)} \right] = \\\\ - \left[ {\underline { + 14 + 2} \,\,\,\,\underline { - 10 - 4} } \right] = - \left[ { + 16 - 14} \right] = - 2\end{array}\)

قرینه 2- نیز 2+ می باشد.

جمع و تفریق عددهای صحیح (به روش ارزش مکانی):

در این روش هر عدد را به همراه علامتش در جدول ارزش مکانی نوشته، با تبدیل آن به یک عبارت، حاصل را به دست می آوریم:

\( - \,15\, + \,61\, - \,38\)

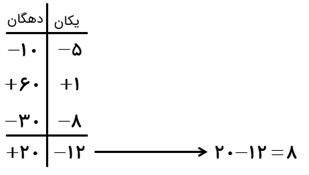
مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

ضرب عددهای صحیح به کمک محور

فصل 2 : عددهای صحیح

از دستور زیر می توان به سادگی به پاسخ رسید:

\(( - \,2)\, \times 3 = - \,6\)

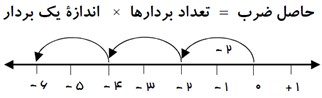
مثال

ضرب متناظر با محور مقابل را بیابید.

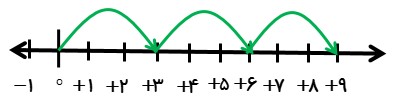
ضرب متناظر آن به صورت زیر است:

\(( + 3)\, \times 3 = + 9\)

نمودار متناظر با ضرب زیر را بنویسید و حاصل را بدست آورید.

\(( - 2)\, \times 4 = \)

نمودار متناظر با ضرب به صورت زیر می شود:

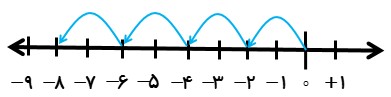
ضرب و تقسیم عددهای صحیح

برای ضرب و تقسیم عددهای صحیح نیز باید دو گام زیر را به ترتیب انجام داد:

گام اول، تعیین علامت حاصل:

اگر علامت ها یک جور بود، علامت حاصل مثبت + و اگر همسان نبود، علامت حاصل منفی خواهد شد.

گام دوم، بدست آوردن جواب:

پس از تعیین علامت، عددها را در هم ضرب یا بر هم تقسیم کنید.

\(( - \,18)\, \div ( + \,3) = - \,6\)

مثال

حاصل عبارت های زیر را بدست آورید.

\(\begin{array}{l}1)\,\,\,( - 100) \div ( + 10) = \\\\2)\,\,( - 4) \times ( + 25) = \\\\3)\,{\kern 1pt} ( - 2) \times ( - 3) \div ( + 6) = \end{array}\)

\(\begin{array}{l}1)\,\,\,( - 100) \div ( + 10) = - 10\\\\2)\,\,( - 4) \times ( + 25) = - 100\\\\3)\,{\kern 1pt} ( - 2) \times ( - 3) \div ( + 6) = ( + 6) \div ( + 6) = + 1\end{array}\)

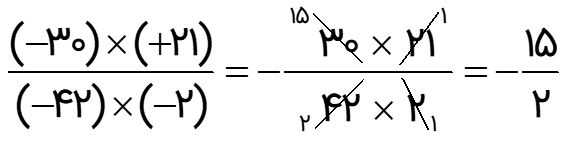
حاصل عبارت \(\frac{{( - 30) \times ( + 21)}}{{( - 42) \times ( - 2)}}\) را بدست آورید.

باید در ساده کردن این طور کسرها دقت کرد. با توجه به جدول ضرب و تقسیم برای علامت های + و – داریم:

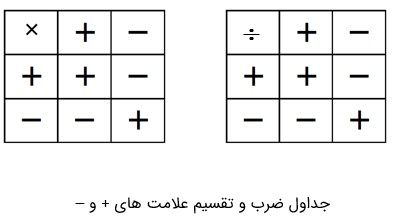
عبارت های ترکیبی

در حل این عبارت ها ابتدا پرانتز (کروشه) را محاسبه و سپس با توجه به علامت بین عددها، حاصل را به دست می آوریم. اگر در یک عبارت ترکیبی پرانتز (کروشه) وجود نداشت، طبق اولویت علامت ها از سمت چپ: یعنی ضرب، تقسیم، جمع و تفریق را انجام دهید:

مثال

حاصل عبارت زیر را بدست آورید.

\(\frac{{ - 30 + 40 - 50 + 60 - \cdots - 210 + 220}}{{ - 150 + 200 - 250 + 300 - \cdots - 1050 + 1100}} = \)

صورت و مخرج کسر را به صورت زیر دسته بندی می کنیم:

\(\begin{array}{l}\frac{{( - 30 + 40) + ( - 50 + 60) + \cdots + ( - 210 + 220)}}{{( - 150 + 200) + ( - 250 + 300) + \cdots + ( - 1050 + 1100)}} = \\\\\frac{{10 + 10 + \cdots + 10}}{{50 + 50 + \cdots + 50}} = \frac{{10 \times 10}}{{50 \times 10}} = \frac{{10}}{{50}} = \frac{1}{5}\end{array}\)

حاصل عبارت \( - \left[ {5\frac{ \circ }{2} \times 3\frac{4}{4} - 12\frac{{48}}{{24}} \times 6\frac{6}{6}} \right]\) را بدست آورید.

دقت کنید عددهایی مانند \(3\frac{4}{4}\) عددهای مخلوط اند که بین عدد و کسر، علامت جمع (به صورت پنهان) وجود دارد:

\(\begin{array}{l}5\frac{ \circ }{2} = 5 + \frac{ \circ }{2} = 5 + \circ = 5\\\\3\frac{4}{4} = 3 + \frac{4}{4} = 3 + 1 = 4\\\\12\frac{{48}}{{24}} = 12 + \frac{{48}}{{24}} = 12 + 2 = 14\\\\6\frac{6}{6} = 6 + \frac{6}{6} = 6 + 1 = 7\\\\ - \left[ {5\frac{ \circ }{2} \times 3\frac{4}{4} - 12\frac{{48}}{{24}} \times 6\frac{6}{6}} \right] = - \left[ {5 \times 4 - 14 \times 7} \right] = \\\\ - \left[ {20 - 98} \right] = - ( - 68) = + 68\end{array}\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

حل مسائل به کمک عددهای صحیح

فصل 2 : عددهای صحیح

گروه اول:

اگر در مسئله ای اختلاف یا فاصله، مانند سردتر، گرمتر و ... خواسته شد، از دستور زیر استفاده کنید:

عدد کوچکتر - عدد بزرگتر = اختلاف

مثال

دمای هوای تهران ۲۸ درجه بالای صفر است. اردبیل ۸ درجه زیر صفر است. اختلاف دمای هوای دو شهر چند درجه است؟

\(( + \,28)\, - \,( - \,8) = 28\, + \,8 = 36\)

گروه دوم:

اگر در مسئله ای میانگین عددها خواسته شد، ابتدا عددها را با هم جمع و سپس حاصل را بر تعداد آنها تقسیم کنید.

مثال

دمای هوا در تبریز دو درجه زیر صفر و دمای اردبیل ۳ برابر آن است. میانگین دمای این دو شهر چند درجه است؟

\(\begin{array}{l}( - \,2) \times 3 = \, - \,6\\\\( - \,6)\, + \,( - \,2) = - \,6\, - \,2 = - \,8\\\\ - \,8\, \div \,2 = - \,4\end{array}\)

گروه سوم:

اگر در مسئله ای هیچ کدام از حالت های قبل وجود نداشت، بین عددها علامت جمع قرار دهید.

مثال

دمای هوای شهر کرد ۳ درجه زیر صفر است. اردبیل ۸ درجه از شهرکرد سردتر است. دمای هوای شهر اردبیل چند درجه است؟

\(( - \,3)\, + \,( - \,8) = - \,11\)

الگو

فصل 3 : جبر و معادله

به رابطه ای منظم بین تعداد بی شمار عدد یا شکل گفته می شود؛ به منظور درک بهتر الگوها، آنها را به گروه های زیر طبقه بندی کرده ایم:

۱- الگوهای عددی و جمله n ام

در این الگوها با توجه به رابطه ای که بین اعداد وجود دارد، می توان به جمله n ام رسید.

مثال

جمله n ام الگوی عددی زیر را نوشته و جمله بیستم آن را حساب کنید.

\(1\,,\,3\,,\,5\,,\,...\)

ملاحظه می شود تفاوت هر جمله با جمله قبلش ۲ می باشد، پس عدد ۲ در تمامی جمله ها ضرب شده که یک واحد از آنها کم شده است. یعنی جمله ام این الگو می شود: \(2\,n - 1\)

\(2(20)\, - \,1 = 40\, - \,1 = 39\) :جمله بیستم

جمله n ام الگوی عددی زیر را بیابید.

\(1\,,\,5\,,\,9\,,\,13\,,\,...\)

ملاحظه می شود تفاوت هر جمله با جمله قبلش 4 می باشد، پس عدد 4 در تمامی جمله ها ضرب شده و مقدار ثابتی از این حاصل ضرب کم شده است که با کمی کنکاش، مقدار ثابت عدد 3- بدست می آید؛ چرا که وقتی جمله اول را بخواهیم بدست آوریم عدد 1 را در 4 ضرب کرده که حاصل ضرب عدد 4 می شود. حال بایستی با چه عددی جمع شود تا حاصل عدد 1 شود؟ درست حدس زدید: عدد 3- . الگوی بدست آمده از توضیحات بالا به صورت زیر می شود:

\(4n - 3\)

برای مطمئن شدن از الگوی n ام بدست آمده، فقط کافی است که مقادیر 2، 3 و ... را در رابطه گذاشته تا جمله های دوم، سوم و ... نیز بدست آید

2- الگو های شکلی و جمله n ام

در این الگوها با توجه به رابطه ای که بین شکل ها وجود دارد، می توان به جمله n ام و شکل مورد نظر رسید.

مثال

جمله n ام الگوی زیر را یافته و بنویسید. شکل دهم این الگو از چند چوب کبریت درست شده است؟

با دقت در شکل ها ملاحظه می شود تفاوت شکل دوم و اول ۳ چوب کبریت می باشد. همچنین تفاوت شکل سوم و دوم نیز 3 چوب کبریت می باشد . در نتیجه جمله n ام مضربی از عدد ۳ خواهد بود که یک واحد به آن اضافه شده است. پس جمله n ام این الگو برابر است با: \(3\,n\, + \,1\)

تعداد چوب کبریت های شکل دهم نیز به این صورت محاسبه می شود:

\(3\,(10)\, + \,1 = 31\)

در الگوی مقابل، شکل n ام چند چوب کبریت و چند مثلث دارد؟

با دقت در شکل ها متوجه می شویم تفاوت شکل بعدی با شکل فعلی، 2 عدد چوب کبریت است، پس شمار تعداد چوب ها از ضرب شماره هر شکل در عدد 2 با جمع یک مقدار ثابت بدست می آید که بعد از کمی دقت متوجه می شویم که این مقدار ثابت عدد 1 می باشد. پس شمار تعداد چوب کبریت های شکل n ام از رابطه زیر بدست می آید:

\(2n + 1\)

و تعداد مثلث در هر شکل با شماره آن شکل یکی است؛ بنابراین تعداد مثلث در شکل n ام برابر همان n می باشد.

3- جمله عمومی مسئله ها

در بعضی از مسائل محاسباتی مربوط به کار در شرکت ها و مکان های اداری، در آمد به صورت هزینه ثابت و هزینه متغیر با مقدار ساعت اضافه کاری محاسبه می شود. در این الگوها ابتدا هزینه ثابت را نوشته و هزینه دیگر را به عنوان ضریب n در نظر گرفته و به آن اضافه می کنیم.

مثال

یک شرکت حمل بار ۳۰۰۰۰ تومان در ابتدای فرداد و به ازای هر ساعت کار ۴۰۰۰ تومان دریافت می کند. برای n ساعت کار چقدر باید پول پرداخت؟

\(30000\, + \,4000\,\,n\,\)

حقوق ثابت رضا 700000 تومان است. اگر به ازای هر ساعت اضافه کاری 20000 تومان به او بدهند، به ازای n ساعت اضافه کاری در ماه، در پایان ماه، حقوق او به چه صورت محاسبه می شود؟

مقدار حقوق \(\; = 700,000\, + \,20,000\,\,n\,\) تومان

4- نوشتن دستور محاسبه محیط و مساحت به صورت جبری

برای این کار با توجه به دستور رسیدن به محیط و مساحت اشکال مختلف و حروفی که روی اضلاع آن شکل آمده، عمل می کنیم.

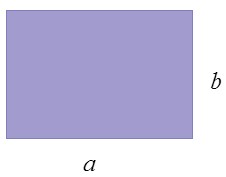
2× (عرض + طول) = محیط مستطیل عرض × طول = مساحت مستطیل

\(P\, = \,(a + b) \times 2\) \(S\, = \,a \times \,b\)

مثال

نسبت مساحت به محیط یک مستطیل به طول a و عرض b را به صورت جبری بدست آورید.

2× (عرض + طول) = محیط مستطیل عرض × طول = مساحت مستطیل

\(S\, = \,a \times \,b\) \(P\, = \,(a + b) \times 2\)

بنابراین:

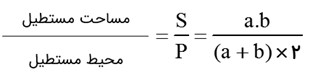
نسبت مساحت به محیط یک دایره را به شعاع R به صورت جبری بدست آورید.

مساحت دایره: \(\;S = \pi {R^2}\)

محیط دایره: \(P = 2\pi R\)

بنابراین:

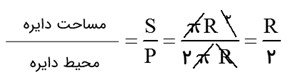
مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

جمله جبری

فصل 3 : جبر و معادله

جمله جبری، کوچکترین بخش از هر عبارت جبری را گویند که شامل دو بخش می باشد:

۱- ضریب عددی:

عددی است که در ابتدای هر جمله جبری قرار گرفته است.

۲- بخش حرفی:

حرف یا حروفی است که بعد از ضریب قرار می گیرند.

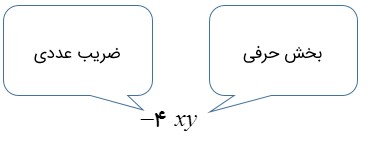
برای جلوگیری از اشتباه شدن علامت ضرب با حرف x در یک عبارت جبری، به جای علامت × از نقطه یا پرانتز و یا از قرار دادن این علامت بطور کلی صرف نظر می کنند؛ مانند:

\(3\, \times \,a\, \times \,b = 3\, \cdot \,a\, \cdot \,b = 3\,(\,a\, \cdot \,b) = 3ab\)

از نوشتن ضریب ۱ می توان صرف نظر کرد:

\(1\, \times \,a\, \times \,b = ab\)

اعداد به تنهایی و بدون حرف خود یک جمله ای جبری به حساب می آیند.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

چند جمله ای

فصل 3 : جبر و معادله

از کنار هم قرار گرفتن چند یک جمله ای که با علامت های جمع یا تفریق از هم جدا شده اند، به وجود می آید؛ مانند:

دو جمله ای\(8\, + \,x\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\)

چهار جمله ای \( - \,b\, - \,8\, + \,7\,x\,y + 2a\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\)

جمله های متشابه

عبارت های جبری هستند که بخش حرفی آنها مثل هم بوده و تفاوت آن ها در ضرایب عددی آنهاست؛ مانند:

\( - \,4\,x\;\;,\;\;\frac{1}{2}\,x\;\;,\;\;9\,x\;\;,\;\; \cdots \)

اعمال جمع، تفریق و ضرب در عبارت های جبری

فصل 3 : جبر و معادله

جمع و تفریق در عبارت های جبری

برای این کار فقط می توان جمله های متشابه را با هم جمع یا از هم کم کرد؛ مانند :

\( - \,4\,x\, + \,5\,x\, - \,2\,x\, = \,(\, - \,4\, + \,5\, - \,2)\,x = \, - \,1\,x = - \,x\)

ساده کردن عبارت های جبری

برای ساده کردن یک عبارت جبری، ابتدا عملیاتی که بین جمله ها وجود دارند را انجام داده، سپس جمله های متشابه را با هم جمع یا از هم کم می کنیم.

اگر هنگام ساده کردن یک عبارت جبری، جمله ای متشابه نداشت، آن جمله را بدون تغییر در مراحل بعد می نویسیم.

ضرب عدد در عبارت جبری

1- ضرب عدد در یک جمله ای:

عدد در ضریب یک جمله ای ضرب می شود؛ مانند:

\( - 2 \times (3x) = - 6x\)

2- ضرب عدد در چند جمله ای:

عدد در تک تک ضرایب یک جمله ای ها ضرب می شود؛ مانند:

\( - 2 \times ( - 3x + 5y) = 6x - 10y\)

ضرب یک جمله ای در چند جمله ای

ابتدا علامت ها، بعد ضرایب عددی و سپس حروف در هم ضرب خواهند شد؛ مانند:

\(2a \times ( - 3x + 7y) = - 6ax + 14ay\)

مثال

عبارت های جبری زیر را ساده کنید.

الف \( - 4ab(\frac{1}{a} - \frac{3}{b}) - \frac{3}{{ab}}( - 2{a^2}b - \frac{4}{6}{b^2}a)\)

ب \( - 2{a^2}b( - 2b + a) + 3b{a^2}( + \frac{1}{3}b - 4a)\)

پ \( - ( - x - 2y - 3z) + 2(z + 2x + 3y) - 4(y - 2z - 3x)\)

الف

\(\begin{array}{l} - 4ab(\frac{1}{a} - \frac{3}{b}) - \frac{3}{{ab}}( - 2{a^2}b - \frac{4}{6}{b^2}a) = \\\underline { - 4b} + \underline{\underline {12a}} + \underline{\underline {6a}} + \underline {2b} = - 2b + 18a = 2(9a - b)\end{array}\)

\(\begin{array}{l} - 2{a^2}b( - 2b + a) + 3b{a^2}( + \frac{1}{3}b - 4a) = \\ + \underline {4{a^2}{b^2}} - \underline{\underline {2{a^3}b}} + \underline {{b^2}{a^2}} - \underline{\underline {12{a^3}b}} = \\5{b^2}{a^2} - 14{a^3}b = {a^2}b( - 14a + 5b)\end{array}\)

\(\begin{array}{l} - ( - x - 2y - 3z) + 2(z + 2x + 3y) - 4(y - 2z - 3x) = \\ + \underline x + \underline{\underline {2y}} + \underline{\underline {\underline {3z} }} + \underline{\underline {\underline {2z} }} + \underline {4x} + \underline{\underline {6y}} - \underline{\underline {4y}} + \underline{\underline {\underline {8z} }} + \underline {12x} = \\17x + 4y + 13z\end{array}\)

مقدار عددی عبارت جبری

برای تعیین این مقدار، به جای حروف موجود در عبارت، اعداد داده شده را می نویسیم؛ مانند:

مثال

مقدار عددی عبارت \(m( - 3m + 1)\) به ازای \(m = - 2\) به دست آورید.

\(\begin{array}{l}m( - 3m + 1)\mathop = \limits^{m = - 2} ( - 2)\left[ { - 3 \times ( - 2) + 1} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - 2 \times 7 = - 14\end{array}\)

اگر 5- = a و 4 = b باشد، حاصل عبارت \( - 3a(1 - b) + \frac{2}{3}b(2a - 1)\) برابر چه عددی می باشد؟

\(\begin{array}{l} - 3a(1 - b) + \frac{2}{3}b(2a - 1) = \\ - 3( - 5)(1 - 4) + \frac{2}{3} \times 4(2( - 5) - 1) = \\45 + \frac{2}{3}( - 44) = 45 - \frac{{88}}{3} = \frac{{135 - 88}}{3} = \frac{{47}}{3}\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

معادله

فصل 3 : جبر و معادله

به یک تساوی جبری که به ازای بعضی از عددها به تساوی عددی تبدیل می شود، «معادله» می گویند.

مراحل حل معادله

1- گام اول، معلوم ، مجهول کردن:

یعنی هر چه متغیر یا مجهول داریم را به یک طرف تساوی و هرچه عدد داریم به طرف دیگر تساوی انتقال دهید. البته توجه داشته باشید در این نقل و انتقال تمام آنچه که منتقل شده اند باید قرینه (علامت آنها عوض) شود.

2- گام دوم، ساده کردن طرفین تساوی:

پس از انجام انتقال، دو طرف تساوی را به ساده ترین صورت در آورید؛ یعنی اگر جمع یا تفریقی در هر طرف تساوی وجود داشت، آنها را انجام دهید.

3- گام آخر، رسیدن به جواب:

جمع عددها را بر مجموع ضرایب تقسیم کنید.

مثال

جواب معادله زیر را به دست آورید.

\(4 - 3x = - 8x - 6\)

\( - 3x + 8x = - 6 - 4\) : گام اول

\(5x = - 10\) : گام دوم

\(x = - \frac{{10}}{5}\) : گام آخر

\(x = - 2\) : جواب معادله

معادلات زیر را حل نمایید.

الف \(\frac{1}{2}x - \frac{1}{3}x + \frac{1}{4}x - \frac{1}{5}x = - 78\)

ب \( - 4(x - 8) = 64\)

پ \(\frac{{2x - 4}}{{3x + 1}} = 0\)

ت \(\frac{{1 - 2x}}{3} - \frac{{4x - 2}}{5} = - 4\)

جواب:

الف

\(\begin{array}{l}\frac{1}{2}x - \frac{1}{3}x + \frac{1}{4}x - \frac{1}{5}x = - 78\\\\ \Rightarrow \frac{{30x - 20x + 15x - 12x}}{{60}} = - 78\\\\ \Rightarrow \frac{{13x}}{{60}} = - 78 \Rightarrow x = \frac{{ - 78 \times 60}}{{13}}\\\\ \Rightarrow x = - 360\end{array}\)

\(\begin{array}{l} - 4(x - 8) = 64\\\\ \Rightarrow x - 8 = \frac{{64}}{{ - 4}} = - 16\\\\ \Rightarrow x = - 16 + 8 \Rightarrow x = - 8\end{array}\)

\(\begin{array}{l}\frac{{2x - 4}}{{3x + 1}} = 0 \Rightarrow 2x - 4 = 0 \Rightarrow 2x = 4\\ \Rightarrow x = \frac{4}{2} \Rightarrow x = 2\end{array}\)

جواب بدست آمده را در مخرج نیز محاسبه می کنیم. اگر مخرج غیر صفر شد، جواب بدست آمده صحیح است؛ در غیر این صورت مسئله جواب ندارد:

\(x = 2 \Rightarrow 3x + 1 = 3(2) + 1 = 7 \ne \circ \)

بنابراین 2 = x جواب مسئله می باشد.

\(\begin{array}{l}\frac{{1 - 2x}}{3} - \frac{{4x - 2}}{5} = - 4\\\\ \Rightarrow \frac{{5(1 - 2x) - 3(4x - 2)}}{{15}} = - 4\\\\ \Rightarrow \frac{{5 - 10x - 12x + 6}}{{15}} = \frac{{ - 22x + 11}}{{15}} = - 4\\\\ \Rightarrow - 22x + 11 = - 60 \Rightarrow - 22x = - 60 - 11\\\\ \Rightarrow - 22x = - 71 \Rightarrow x = \frac{{71}}{{22}}\end{array}\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

امتحان جواب معادله

فصل 3 : جبر و معادله

برای امتحان درست بودن حل یک معادله، باید جواب (جواب های) به دست آمده را در صورت معادله به جای مجهول قرار دهید. اگر دو طرف تساوی یک اندازه شد، جواب صحیح و معادله درست حل شده است.

حل مسائل به کمک معادله با تبدیل صورت

بسیاری از مسائل به معادله، می توان با سرعت و دقت به جواب رسید. برای این کار ابتدا خواسته مسئله را با x مشخص کرده و سپس اطلاعات مسئله را به علائم ریاضی تبدیل کنید. به مثال های زیر توجه نمایید:

مثال

از دو برابر عددی پنج واحد کم کردیم، حاصل منفی هفت شد. عدد چیست؟

عدد مورد نظر را x فرض می کنیم. پس داریم:

عدد مورد نظر = مقدار کم شده - (عدد × ۲)

\(\begin{array}{l}(2 \times x) - 5 = - 7\\\\2x - 5 = - 7\\\\2x = - 7 + 5 = - 2\\\\x = - \frac{2}{2}\\x = - 1\end{array}\)

مثال

حاصل جمع سه عدد صحیح متوالی ۳۳- می باشد. آن سه عدد کدامند؟

با توجه به این که سه عدد متوالی هستند، پس داریم:

\(x\) : عدد مورد نظر

\(x - 1\) : عدد کوچک تر

\(x + 1\) : عدد بزرگ تر

\(\begin{array}{l}(x - 1) + x + (x + 1) = - 33\\\\3x = - 33\\\\x = - \frac{{33}}{3}\end{array}\)

\(x = - 11\) : عدد مورد نظر

\((x - 1) = - 11 - 1 = - 12\) : عدد کوچک تر

\((x + 1) = - 11 + 1 = - 10\) : عدد بزرگ تر

خط

فصل 4 : هندسه و استدلال

خط از کنار هم قرار گرفتن بی شمار نقطه در کنار هم به وجود می آید.

انواع خط

1- خط راست.

2- خط شکسته.

3- خط خمیده (منحنی).

نام گذاری نقطه و خط

در ریاضیات برای نام گذاری شکل ها از حروف انگلیسی استفاده می کنیم. به طور معمول نقطه را با حروف بزرگ انگلیسی نام گذاری می کنیم و برای نام گذاری امتداد خط که در شکل با فلش نشان می دهیم از حروف کوچک استفاده می کنیم؛ مانند:

از یک نقطه بی شمار خط می گذرد.

از دو نقطه فقط یک خط راست می گذرد.

از دو نقطه بی شمار خط خمیده و شکسته می گذرد.

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

پاره خط و نیم خط

فصل 4 : هندسه و استدلال

پاره خط

قسمتی از یک خط که با دو نقطه جدا شده باشد.

طول یا اندازه پاره خط:

طول یک پاره خط را با قرار دادن یک پاره خط کوچک در بالای نام آن نمایش می دهیم؛ برای مثال \(\overline {AB} \) یعنی طول پاره خط AB و آن فاصله بین دو سر پاره خط می باشد که با واحدی به نام سانتیمتر (cm) اندازه گیری می شود.

تعداد تمام پاره خط های روی یک خط از این دستور محاسبه می شود:

\(\frac{{n(n - 1)}}{2}\)

در این فرمول n تعداد نقطه ها می باشد.

مثال

اگر روی خطی 7 نقطه قرار دهیم، چند پاره خط روی آن ایجاد می شود؟

در این مثال 7 نقطه داریم (7 = n):

تعداد پاره خط ها \( = \frac{{n(n - 1)}}{2} = \frac{{7(7 - 1)}}{2} = \frac{{7 \times 6}}{2} = 21\)

روی خطی n نقطه قرار دارد. اگر 3 نقطه به این n نقطه اضافه کنیم، چند پاره خط به تعداد پاره خط ها اضافه می شود؟

ابتدا تعداد پاره خط ها را در هر حالت بدست می آوریم:

تعداد نقطه : حالت اول \( = n \Rightarrow \) تعداد پاره خط ها \( = \frac{{n(n - 1)}}{2}\)

عداد نقطه : حالت دوم \( = n + 3 \Rightarrow \) تعداد پاره خط ها \( = \frac{{(n + 3)(n + 3 - 1)}}{2}\)

تعداد پاره خط های اضافه شده \( = \frac{{(n + 3)(n + 2)}}{2} - \frac{{n(n - 1)}}{2}\)

\( = \frac{{{n^2} + 5n + 6 - {n^2} + n}}{2} = \frac{{4n + 6}}{2} = 2n + 3\)

تعداد 3 + n2 پاره خط اضافه می شود.

نیم خط

قسمتی از یک خط که از یک طرف با یک نقطه جدا شده باشد . نیم خط را ابتدا با نام نقطه و سپس نام خط نام گذاری می کنند و می خوانند؛ مانند نیم خط Ax

تعداد تمام نیم خط های روی یک خط از دستور n2 به دست می آید که در آن n تعداد نقطه ها می باشد.

مثال

اگر روی خطی 6 نقطه قرار دهیم، چند نیم خط ایجاد می شود؟

12 = 6 × 2 = تعداد نیم خط ها

در شکل مقابل چند پاره خط وجود دارد؟

از آنجایی که روی هر پاره خط افقی 6 نقطه وجود دارد، با توجه به مطالب بالا، تعداد پاره خط های روی آن ها برابر است با:

\(\frac{{n(n - 1)}}{2} = \frac{{6(6 - 1)}}{2} = 15\)

تعداد کل پاره خط های افقی \( = 5 \times 15 = 75\)

از طرفی 6 پارخط عمودی داریم که روی هر یک از آن ها 5 نقطه وجود دارد:

\(\frac{{n(n - 1)}}{2} = \frac{{5(5 - 1)}}{2} = 10\)

تعداد کل پاره خط های عمودی \( = 6 \times 10 = 60\)

در مجموع، تعداد کل پاره خط ها به صورت زیر محاسبه می شود:

تعداد کل پاره خط ها \( = 75 + 60 = 135\)

مقایسه پاره خط ها

پاره خط ها را با توجه به طول آنها با هم مقایسه می کنیم.

مثلا پاره خط AB بزرگتر از پاره خط EF می باشد. این موضوع را به صورت ریاضی چنین می نویسیم.

جمع و تفریق پاره خط ها

در جمع پاره خط ها به دنبال هم و در تفریق، آنها را روی هم قرار می دهیم؛ مانند:

در شکل نقاطA،B و C روی یک خط قرار دارند. داریم:

\(\begin{array}{l}AB + BC = AC\\AC - AB = BC\\AC - BC = AB\end{array}\)

نسبت بین پاره خط ها

با توجه به طول پاره خط ها می توان بین آنها نسبت های مختلفی به دست آورد؛ مانند:

در شکل M وسط پاره خط AB است.

\(\begin{array}{l}\overline {AB} = 2\overline {MB} \\\overline {AM} = \frac{1}{2}\overline {AB} \end{array}\)

روابط بین پاره خط ها

با شناخت رابطه بین چند پاره خط ها می توان به رابطه های دیگری رسید؛ مانند:

\(\left. \begin{array}{l}\overline {AB} = \overline {CD} \\\overline {AB} > \overline {EF} \end{array} \right\}\;\;\;\; \Rightarrow \;\;\;\;\overline {CD} > \overline {EF} \)

مثال

در شکل زیر، طول نقاط A و B مشخص شده است. اگر \(\overline {AB} = 2\overline {BC} \) و \(\overline {BC} = 3\overline {CD} \) باشد، طول نقاط C و D کدام است؟

روی محور اعداد صحیح، طول نقطه A را با x_A نشان می دهند:

\(\begin{array}{l}\overline {AB} = {x_B} - {x_A} = 10 - 4 = 6\\\overline {AB} = 2\overline {BC} = 6 \Rightarrow \overline {BC} = 3\\\overline {BC} = 3\overline {CD} = 3 \Rightarrow \overline {CD} = 1\\\overline {BC} = 3 \Rightarrow {x_C} - {x_B} = {x_C} - 10 = 3 \Rightarrow {x_C} = 13\\\overline {CD} = 1 \Rightarrow {x_D} - {x_C} = {x_D} - 13 = 1 \Rightarrow {x_D} = 14\end{array}\)

دو خطی که بر خط سومی عمود باشند، نسبت به هم .......... .

موازی هستند.

می خواهیم یک طناب 30 متری را به بیشترین قطعات ممکن با طول هایی که عدد طبیعی بیشتر از 1 هستند، تقسیم کنیم. چند برش لازم داریم؟

هر قطعه طناب می تواند 2 متر باشد؛ یعنی 15 قطعه که 14 برش نیاز دارد.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

زاویه، انواع آن و روابط بین آن ها

فصل 4 : هندسه و استدلال

زاویه

دو نیم خط با رأس مشترک، زاویه ایجاد می کنند.

نام گذاری زاویه:

1- با حرف رأس:

یک حرف بزرگ انگلیسی

2- با حرف رأس و دو نیم خط:

سه حرف انگلیسی که حرف وسط (همان رأس) حرف بزرگ و حروف کناری (نیم خط ها) حرف کوچک استفاده می شود.

مانند:

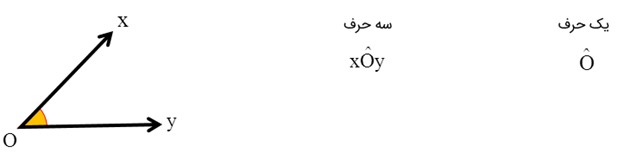
مثال

اگر ضلع های زاویه ای را چهار برابر کنیم، اندازه زاویه ... .

تغییری نمی کند.

اندازه زاویه هیچ ربطی به اندازه های ضلع های آن ندارد، پس هر چه اندازه های ضلع ها تغییر کنند، اندازه زاویه را تغییری نمی دهند.

انواع زاویه

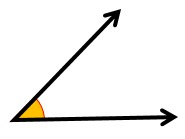
1- زاویه تند یا حاده:

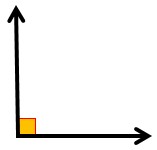
2- زاویه راست یا قائمه:

3- زاویه باز یا منفرجه:

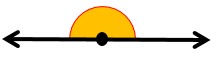
4- زاویه نیم صفحه یا تخت:

5- زاویه مقعر یا کاو (از ۱۸۰ تا ۳۶۰ درجه):

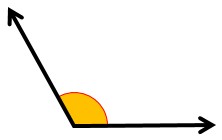
6- زاويه محدب یا کوژ (کمتر از ۱۸۰ درجه):

مثال

با توجه به شکل،

الف چند زاویه قائمه در شکل وجود دارد؟

ب به طور کلی چند زاویه در این شکل موجود است؟

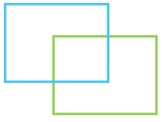
الف

زاویه قائمه زاویه ای است که 90 باشد. در شکل زیر، همه زاویه های قائمه مشخص شده اند (16 تا):

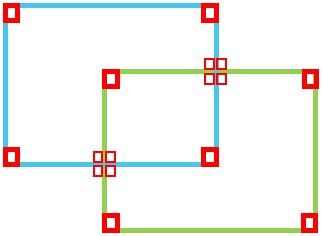
ب به طور کلی 16 زاویه در شکل موجود است.

زاویه های متمم:

دو زاویه (خواه کنار هم، خواه جدا از هم) که مجموع آنها ۹۰ درجه شود.

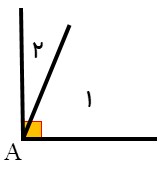
\({\hat A_1} + {\hat A_2} = {90^ \circ }\)

زاویه های مکمل:

دو زاویه (خواه کنار هم، خواه جدا از هم) که مجموع آنها 180 درجه شود.

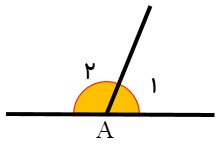
\({\hat A_1} + {\hat A_2} = {180^ \circ }\)

زاویه های متقابل به رأس:

دو زاویه که در رأس مشترک و اضلاع آنها در امتداد هم باشند.

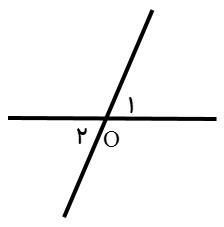
\({\hat O_1} = {\hat O_2}\)

دو زاویه متقابل به رأس همیشه با هم مساویند.

مثال

دو زاویه متقابل به رأس، مکمل اند، اندازه هر کدام برابر چند است؟

دو زاویه متقابل به رأس و مکمل \(\hat A\) و \(\hat B\) را در نظر بگیری:

\(\left. \begin{array}{l}\hat A = \hat B\\\hat A + \hat B = {180^ \circ }\end{array} \right\} \Rightarrow \hat A = \hat B = {90^ \circ }\)

روابط بین زاویه ها

با شناخت رابطه بین چند زاویه، می توان به رابطه های دیگری رسید؛ مانند:

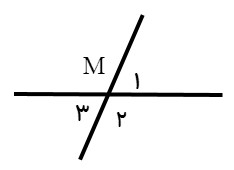
\(\left. \begin{array}{l}{{\hat M}_1} + {{\hat M}_2} = {180^ \circ }\\{{\hat M}_2} + {{\hat M}_3} = {180^ \circ }\end{array} \right\}\;\;\; \Rightarrow \;\;\;{\hat M_1} = {\hat M_3}\)

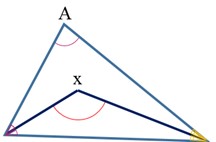
مثال

در مثلث زیر، زاویه A برابر با 80 درجه است. اگر نیمسازهای دو زاویه دیگر را رسم کنیم، اندازه زاویه x را بدست آورید.

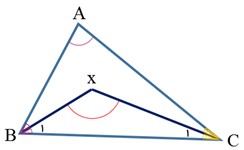
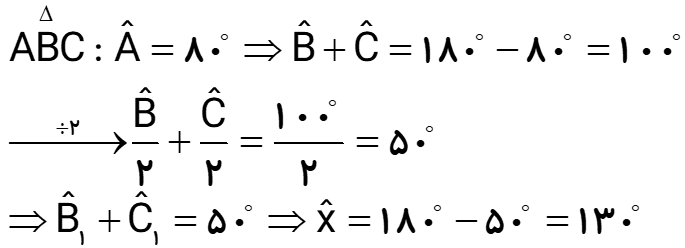
در شکل روبرو، زاویه x چند درجه است؟

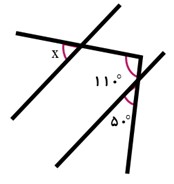
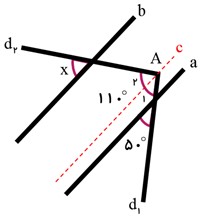
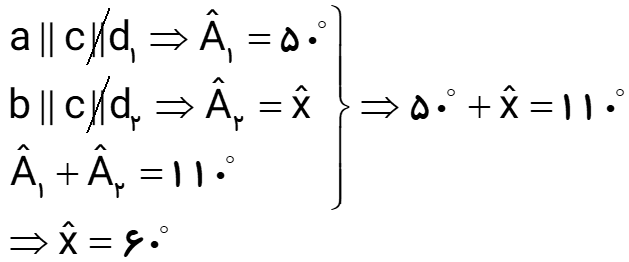
در شکل مقابل، مثلث متساوی الاضلاع CDE روی مربّع ABCD قرار دارد. زاویه BDC چند درجه است؟

از آنجایی که هر زاویه مثلث متساوی الاضلاع 60 درجه و هر زاویه مربع 90 درجه است و در مثلث متساوی الاضلاع، هر سه ضلع و هر سه زاویه برابر است، داریم:

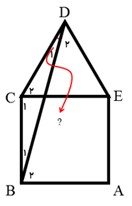
متساوی الاضلاع \(\,D\mathop C\limits^\Delta E \Rightarrow \overline {DC} = \overline {CE} \)

مربع \(ABCD \Rightarrow \overline {CE} = \overline {BC} \)

مثلث متساوی الساقین \(A\mathop E\limits^\Delta D \Rightarrow {\hat B_1} = {\hat D_1}\) \( \Rightarrow \overline {CD} = \overline {BC} \Rightarrow \)

\(\begin{array}{l}\left. \begin{array}{l}{{\hat C}_1} = {90^ \circ }\\{{\hat C}_2} = {60^ \circ }\end{array} \right\} \Rightarrow \hat C = {{\hat C}_1} + {{\hat C}_2} = {90^ \circ } + {60^ \circ } = {150^ \circ }\\\\{{\hat D}_1} + {{\hat B}_1} = {180^ \circ } - \hat C = {180^ \circ } - {150^ \circ } = {30^ \circ }\\\\{{\hat D}_1} = {{\hat B}_1} \Rightarrow 2{{\hat D}_1} = {30^ \circ } \Rightarrow {{\hat D}_1} = {15^ \circ }\end{array}\)

زاویه بین عقربه های ساعت

زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت h و دقیقه m از رابطه زیر به دست می آید:

\(\hat A = \left| {30h - \frac{{11}}{2}m} \right|\)

البته اگر مقدار زاویه بدست آمده بیشتر از 180 درجه شد، زاویه بدست آمده را از 360 درجه کم می کنیم.

مثال

زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت زیر را بیابید.

ساعت اکنون 10:10 می باشد که در این صورت:

\(h = 10\,\;\,\,\,\,,\;\,\,\,\,m = 10\)

\(\begin{array}{l}\hat A = \left| {30h - \frac{{11}}{2}m} \right| = \left| {30 \times 10 - \frac{{11}}{2} \times 10} \right| = \\\\300 - 55 = {245^ \circ }\end{array}\)

چون مقدار 245 درجه از 180 درجه بیشتر است، این عدد را از 360 درجه کم می کنیم:

\({360^ \circ } - {245^ \circ } = {115^ \circ }\)

در نتیجه زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت برابر 115 درجه می باشد.

زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت 6:15 را بیابید.

\(\begin{array}{l}h = 6\,\;\,\,\,\,,\;\,\,\,\,m = 15\\\\\hat A = \left| {30h - \frac{{11}}{2}m} \right| = \left| {30 \times 6 - \frac{{11}}{2} \times 15} \right| = \\\\180 - 82/5 = - {97/5^ \circ }\end{array}\)

چند ضلعی ها

فصل 4 : هندسه و استدلال

مثلث

در هر مثلث مجموع زاویه ها برابر ۱۸۰ درجه است.

مثلث ها را با توجه به اندازه زاویه هایشان به سه دسته تقسیم می کنیم:

1) مثلث هایی که هر سه زاویه آنها تند است.

2) مثلث هایی که یک زاویه راست دارند.

3) مثلث هایی که یک زاویه باز دارند.

4) یک مثلث را وقتی نمی توان کشید که اندازه هر ضلع آن مساوی با بزرگتر از جمع دو ضلع دیگرش باشد:

جمع دو ضلع دیگر > اندازه هر ضلع

5) مثلث مختلف الاضلاع را می توان با «سه زاویه تند» یا «یک زاویه قائمه و دو زاویه تند» و یا «یک زاویه باز و دو زاویه تند» رسم کرد.

6) مثلث متساوی الساقین را می توان با «سه زاویه تند» یا «یک زاویه قائمه و دو زاویه تند» و با «یک زاویه باز و دو زاویه تند» رسم کرد.

7) مثلث متساوی الاضلاع را فقط با سه زاویه تند ( زاویه 60 درجه) می توان رسم کرد.

مثال

آیا با عدد های 5، 12 و 13 می توان مثلث رسم کرد؟

جهت رسم یک مثلث، برای تمام اضلاع باید رابطه زیر برقرار باشد:

جمع دو ضلع دیگر > اندازه هر ضلع

بنابراین:

\(\begin{array}{l}5 < 12 + 13 = 25\\\\12 < 5 + 13 = 18\\\\13 < 5 + 12 = 17\end{array}\)

پس با این اضلاع حتما می توان یک مثلث رسم کرد.

طول دو ضلع مثلثی 7 و 4 می باشد. اندازه ضلع سوم را بررسی کنید.

همان طور که می دانیم برای رسم یک مثلث بایستی هر سه ضلع از قانون زیر تبعیت کنند:

جمع دو ضلع دیگر > اندازه هر ضلع

بنابراین:

\(\,\, < 4 + 7 = 11\)اندازه ضلع سوم

اندازه ضلع سوم باید حتما کمتر از 11 باشد.

نکاتی درباره چند ضلعی ها

1 چند ضلعی هایی که هیچ زاویه بزرگتر از ۱۸۰ درجه ندارند، «چند ضلعی محدب یا کوژ» نامیده می شوند.

2 به چند ضلعی ای که دست کم یک زاویه بزرگتر از ۱۸۰ داشته باشد، «چند ضلعی مقعر یا کاو» می گویند.

3 به چند ضلعی هایی که همۀ ضلع ها و زاویه هایشان با هم مساوی است، «چند ضلعی منتظم» گفته می شود، مانند مثلث متساوی الاضلاع، مربع و ... .

4 مجموع زاویه های هر n ضلعی برابر است با:

\((n - 2) \times 180\)

که n تعداد اضلاع است.

5 اندازه هر زاویه هر n ضلعی منتظم برابر است با:

\(\frac{{180 \times (n - 2)}}{n}\)

6 تعداد قطرهای هر n ضلعی برابر است با:

\(\frac{{n \times (n - 2)}}{2}\)

مثال

مجموع زوایای یک 8 ضلعی را بیابید.

\(\begin{array}{l}n = 8\\\\ \Rightarrow (n - 2) \times {180^ \circ } = (8 - 2) \times {180^ \circ } = 6 \times {180^ \circ } = {720^ \circ }\end{array}\)

تعداد قطرهای یک 8 ضلعی را بیابید.

\(\begin{array}{l}n = 8\\\\ \Rightarrow \frac{{n \times (n - 2)}}{2} = \frac{{8 \times (8 - 2)}}{2} = \frac{{8 \times 6}}{2} = \frac{{48}}{2} = 24\end{array}\)

اندازه یک زاویه داخلی 5 ضلعی منتظم را بیابید.

\(\begin{array}{l}n = 5\\\\ \Rightarrow \frac{{{{180}^ \circ } \times (n - 2)}}{n} = \frac{{{{180}^ \circ } \times (5 - 2)}}{5} = \\\\\frac{{{{180}^ \circ } \times 3}}{5} = \frac{{{{540}^ \circ }}}{5} = {108^ \circ }\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

تبدیلات هندسی (انتقال، تقارن و دوران)

فصل 4 : هندسه و استدلال

اگر شکل را بدون تغییر جهت روی صفحه حرکت دهید تا تصویر آن جابجا گردد، بدین ترتیب شکل را روی صفحه انتقال داده اید.

وقتی قرینه شکلی را نسبت به یک خط (خط تقارن) پیدا می کنیم، تصویر به دست آمده مساوی آن شکل است، اما جهت آن تغییر می کند.

مرکز دوران:

نقطه ای است که شکل حول آن گردش (یا دوران) می کند.

در دوران ۱۸۰ درجه نسبت به مرکز دوران، شکل به اندازه یک زاویه نیم صفحه (۱۸۰ درجه) گردش خواهد داشت.

در دوران ۹۰ درجه نسبت به مرکز دوران، شکل به اندازه یک زاویه قائمه (۹۰ درجه) گردش می کند. این گردش به دو صورت امکان پذیر است. خلاف عقربه های ساعت، که گردش ۹۰ درجه به سمت راست و در جهت عقربه های ساعت که گردش ۹۰ به سمت چپ شکل اولیه صورت می گیرد.

مثال

کدام یک از گزینه های زیر دوران یافته شکل مقابل است؟

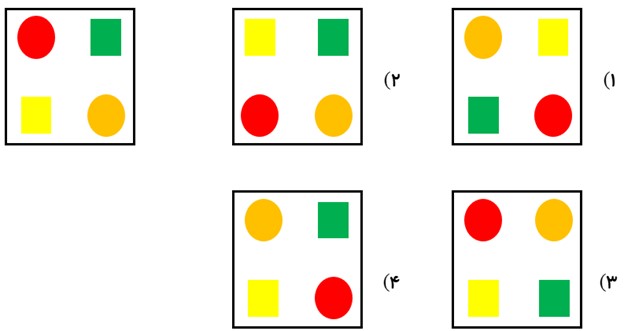
گزینه (1) جواب صحیح می باشد.

شکل های مساوی (هم نهشت)

اگر بتوانیم شکلی را با یک یا چند تبدیل انتقال، تقارن یا دوران در صفحه بر شکل دیگر منطبق کنیم، می گوییم این دو شکل با هم هم نهشت (مساوی) اند. این تبدیل ها به ← مشخص می گردد که نوع تبدیل بالای فلش نوشته می شود.

مثال

اگر دو شکل زیر هم نهشت باشند، مقادیر x و y را بیابید.

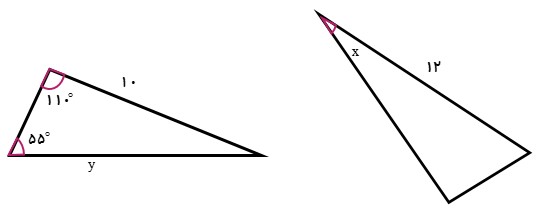
ابتدا راس هر مثلث را نام گذاری می کنیم تا اضلاع و زاویه های متناظر را تعیین کنیم:

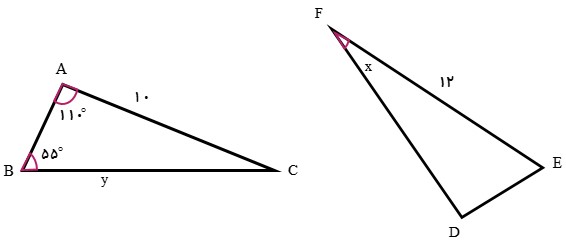
\(\left\{ \begin{array}{l}\hat A = \hat D\\\hat B = \hat E\\\hat C = \hat F\end{array} \right.\,\,\,\,\,\,,\,\,\,\,\,\,\,\left\{ \begin{array}{l}\overline {AB} = \overline {DE} \\\overline {AC} = \overline {DF} \\\overline {BC} = \overline {EC} \end{array} \right.\)

در نتیجه مقادیر x و y به صورت زیر می باشند:

\(\begin{array}{l}x = \hat F = \hat C = {180^ \circ } - (\hat A + \hat B)\\\\ \Rightarrow x = {180^ \circ } - ({110^ \circ } + {55^ \circ }) = {15^ \circ }\\\\y = \overline {BC} = \overline {EF} \Rightarrow y = 12\end{array}\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

شمارنده ها و اعداد اول

فصل 5 : شمارنده ها و اعداد اول

شمارنده ها (مقسوم علیه های) یک عدد

در ریاضیات اگر عددی طبیعی مانند a بر عددی طبیعی مانند b بخش پذیر باشد، b را شمارنده یا مقسوم علیه a گویند. به بیان دیگر باقیمانده a بر b برابر صفر می شود؛ مانند: 1، 2، 3، ۶ و ۱۲ که همگی شمارنده های عدد ۱۲ می باشند.

12 و 6 و 4 و 3 و 2 و 1= شمارنده های ۱۲

عدد اول

اعداد طبیعی هستند که فقط دو شمارنده دارند، یکی عدد ۱ و دیگری خود عدد؛ مانند:

۱ و ۱۱ = شمارنده های ۱۱

۱ و ۲ = شمارنده های ۲

عدد ۱ نه اول است و نه غیر اول (مرکب)، بلکه به آن «بسیط» یا «ساده» می گویند.

شمارنده های اول

به شمارنده هایی که عدد اول باشند، «شمارنده های اول» گفته می شود.

برای رسیدن به شمارنده های اول می توان از روش های زیر استفاده کرد:

۱) نوشتن تمامی شمارنده های عدد مورد نظر و مشخص کردن شمارنده های اول آن.

۲) استفاده از نمودار درختی یا تجزیه کردن (نوشتن عدد به صورت ضرب عامل های اول

استفاده از قواعد بخش پذیری اعداد اول

فصل 5 : شمارنده ها و اعداد اول

1- بخش پذیری بر ۲:

یکان عدد زوج باشد.

2- بخش پذیری بر ۳:

جمع رقم ها مضرب ۳ باشد.

3- بخش پذیری بر ۴:

دو برابر دهگان را با یکان جمع می کنیم و باقیمانده ی تقسیم عدد حاصل بر ۴ را به دست می آوریم. اگر باقیمانده صفر شد. عدد بر ۴ بخش پذیر است.

باقیمانده تقسیم عدد 14 بر 4 برابر 2 می باشد\(2\underline 5 4\;\; \to \;\;2 \times 5 + 4 = 10 + 4 = 14\;\; \Rightarrow \;\;\)

4- بخش پذیری بر ۵:

یکان 0 یا ۵ باشد.

5- بخش پذیری بر ۶:

اعداد زوجی که بر 3 بخش پذیر باشد بر ۶ بخش پذیرند. در واقع اگر عددی هم بر ۲ و هم بر ۳ بخش پذیر است، بر ۶ نیز بخش پذیر خواهد بود.

1 حاصل ضرب سه عدد متوالی بر 6 بخش پذیر است:

\(\begin{array}{l}(2,\,3,\,4)\;\;\;\;\;\;\;\;\;\;\;\;\;\;2 \times 3 \times 4 = 24\\(3,\,4,\,5)\;\;\;\;\;\;\;\;\;\;\;\;\;\;3 \times 4 \times 5 = 60\end{array} \)

2 حاصل ضرب دو عدد فرد یک عدد فرد است.

\(3 \times 5 = 15\)

3 حاصل ضرب دو عدد زوج یک عدد زوج است.

\(2 \times 12 = 24\)

4 حاصل ضرب یک عدد زوج در یک عدد فرد، یک عدد زوج است.

\(5 \times 4 = 20\)

6- بخش پذیری بر ۷:

عدد حاصل از مجموع پنج برابر یکان و بقیه رقم ها، مضرب ۷ باشد؛ مانند:

\(231\;\,\, \to \;\;(1 \times 5) + 23 = 28 = 14\;\,\, \to \;\;28 = 7 \times 4\)

7- بخش پذیری بر ۹:

جمع رقم ها مضرب ۹ باشد.

8- بخش پذیری بر ۱۱:

الف) دو رقمی:

ارقام تکراری؛ مانند : ۷۷ یا ۴۴

ب) سه رقمی:

رقم وسط برابر جمع دو رقم کناری شود؛ مانند: ۱۷۶ یا ۳۵۲ و ... .

پ) چند رقمی:

رقم های عدد مورد نظر را یکی در میان جمع می کنیم. حاصل جمع دو گروه را از هم کم می کنیم. اگر این حاصل 0 یا مضرب ۱۱ شد، عدد پر ۱۱ بخش پذیر می باشد.

\(4136\,\,\,\;\;\left. \begin{array}{l}4 + 3 = 7\\1 + 6 = 7\end{array} \right\}\, \Rightarrow \,7 - 7 = 0\)

9- بخش پذیری بر ۱۳:

حاصل مجموع چهار برابر یکان و بقيه رقم ها، مضرب ۱۳ باشد؛ مانند:

\(65\;\,\, \to \;\;(5 \times 4) + 6 = 26\;\,\, \to \;\;26 = 13 \times 2\)

مثال

مجموع سه عدد فرد متوالی همواره بر کدام یک از عددهای اول تک رقمی بخش پذیر است؟

: مجموع سع عدد فرد متوالی

\((2k + 1) + (2k + 3) + (2k + 5) = 6k + 9 = 3(2k + 3)\)

پس مجموع سه عدد فرد متوالی بر 3 بخش پذیر است.

مثال

مقدار x چند باشد تا عدد نُه رقمی \(\overline {b458abxa5} \) بر 11 بخش پذیر باشد؟

در بخش پذیری بر عدد 11 داشتبم که رقم های عدد را از سمت راست شماره گذاری می کنیم. مجموع رقم های شماره فرد را از مجموع رقم های شماره زوج کم می کنیم. عدد حاصل باید بر 11 بخش پذیر باشد:

\(a + b + 8 + 4 = a + b + 12\) : مجموع رقم های شماره زوج

\(5 + x + a + 5 + b = x + a + b + 10\) : مجموع رقم های شماره فرد

= مجموع رقم های شماره فرد – مجموع رقم های شماره زوج

\((a + b + 12) - (x + a + b + 10) = 2 - x\)

حال عبارت بدست آمده باید صفر و یا مضربی از عدد 11 باشد و چون x یک عدد تک رقمی است، پس حاصل x – 2 بایستی صفر باشد. در نتیجه:

\(2 - x = 0 \Rightarrow x = 2\)

اگر x11 بر y7 بخش پذیر باشد، چه نتیجه ای می توان گرفت؟

x11 بر y7 بخش پذیر است. چون دو عدد 11 و 7 عامل مشترک ندارند (عدد اول هستند)، باید x عددی باشد که بعد از ضرب شدن در 11 بر y7 بخش پذیر شود؛ پس x حتما بر 7 بخش پذیر خواهد بود.

اگر عدد \(\overline {854x3y} \) بر 6 بخش پذیر باشد، بیشترین مقدار y + x را بیابید.

عددی که بر 6 بخش پذیر است، 2 شرط دارد:

شرط اول: عدد زوج باشد، یعنی بر 2 بخش پذیر باشد؛ در نتیجه y زوج می باشد.

شرط دوم: عدد مورد نظر بر 3 نیز بخش پذیر باشد؛ بنابراین:

\(\begin{array}{l}8 + 5 + 4 + x + 3 + y = 20 + x + y\\ \Rightarrow \\x + y = 1\\x + y = 4\\x + y = 7\\x + y = 10\\x + y = 13\\x + y = 16 \to x = 8\,\,\,\,\,,\,\,\,\,\,y = 8\end{array}\)

بیشترین مقدار برای y + x ، 16 است.

اگر حاصل ضرب دو عدد اوّل 91 باشد، حاصل جمع آن ها را بیابید.

\(91 = 13 \times 7 \Rightarrow 13 + 7 = 20\)

به چند حالت می توان با 28 دانش آموز تعدادی صف تشکیل داد؟

به 7 حالت می توان با 28 دانش آموز صف تشکیل داد. \(28 = \left\{ \begin{array}{l}28 \times 1\\14 \times 2\\7 \times 4\\4 \times 7\\2 \times 14\\1 \times 28\end{array} \right. \Rightarrow \)

در الگوریتم غربال برای تعیین اعداد اول 1 تا 100، پنجاه و هفتمین عددی که خط می خورد، کدام است؟

در ابتدا عدد 1 و سپس مضرب های 2 (به غیر از خود عدد 2) خط می خورند (تا الان 50 عدد خط خورده اند و می ماند 7 عدد دیگر تا به جواب برسیم). سپس همه مضرب هایی از 3 که بار اول خط نخورده اند (طبیعتاً به غیر از خود عدد 3) و بعد از پنجاهمین عدد قرار دارند، خط می خورند. در نتیجه پنجاه و هفتمین عدد، 45 است:

\(\begin{array}{*{20}{c}}9&{15}&{21}&{27}&{33}&{39}&{45}\\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow \\{51}&{52}&{53}&{54}&{55}&{56}&{57}\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

ب.م.م، ک.م.م و نمودار درختی

فصل 5 : شمارنده ها و اعداد اول

بزرگ ترین شمارنده مشترک (ب.م.م)

شمارنده های یک عدد را مقسوم علیه های آن نیز می گویند؛ بنابراین بزرگ ترین شمارنده مشترک دو عدد همان بزرگ ترین مقسوم علیه مشترک است که به اختصار آن را ب.م.م می نویسند. ب.م.م دو عدد را به صورت \((\,\,\,\,\,,\,\,\,\,\,)\) نشان می دهند.

کوچک ترین مضرب مشترک (ک.م.م)

کوچک ترین مضرب مشترک دو عدد، اولین مضرب مشترک آن دو عدد است. کوچک ترین مضرب مشترک دو عدد را به طور اختصار ک.م.م می گویند و به صورت \(\left[ {\,\,\,\,\,,\,\,\,\,\,} \right]\) نمایش می دهند.

دستور برای یافتن ب.م.م و ک.م.م

پس از تجزیه عددها به شمارنده های اول آنها از دستورهای زیر برای یافتن ب.م.م و ک.م.م استفاده می کنیم:

ب.م.م \((\,\,\,\,\,,\,\,\,\,\,)\) :

شمارنده های مشترک با کمترین تکرار

ک.م.م \(\left[ {\,\,\,\,\,,\,\,\,\,\,} \right]\) :

شمارنده های غیر مشترک x شمارنده های مشترک با بیشترین تکرار

نمودار درختی

هرگاه عددی طبیعی را به صورت ضرب دو عدد غیر از ۱ به دوشاخه در آوریم (بهتر است این ضرب از یک عدد اول و یک عدد غير اول تشکیل شود) و این کار را ادامه دهیم، به شمارنده های اول آن عدد خواهیم رسید؛ مانند:

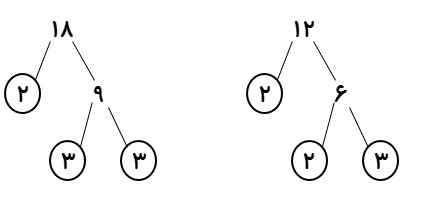
\(\begin{array}{l}18 = 2 \times 3 \times 3\\\\12 = 2 \times 2 \times 3\\\\\left( {18\;,\;12} \right) = 2 \times 3 = 6\\\\\left[ {18\;,\;12} \right] = 2 \times 2 \times 3 \times 3 = 36\end{array}\)

مثال

بزرگ ترین مقسوم علیه مشترک دو عدد A و B را بیابید.

\(\left\{ \begin{array}{l}A = {2^2} \times {3^3} \times 5\\B = 2 \times 3 \times {5^2}\end{array} \right.\)

\(\left\{ \begin{array}{l}A = {2^2} \times {3^3} \times 5\\B = 2 \times 3 \times {5^2}\end{array} \right. \Rightarrow \left( {A\,,\,B} \right) = 2 \times 3 \times 5 = 30\)

ک.م.م دو عدد 48 و 36 را بیابید.

\(\left\{ \begin{array}{l}48 = {2^4} \times 3\\36 = {2^2} \times {3^2}\end{array} \right. \Rightarrow \left[ {48\,,\,36} \right] = {2^4} \times {3^2} = 144\)

نمودار درختی دو عدد 144 و 96 را رسم کرده، ب.م.م و ک.م.م هر دو عدد را مشخص کنید.

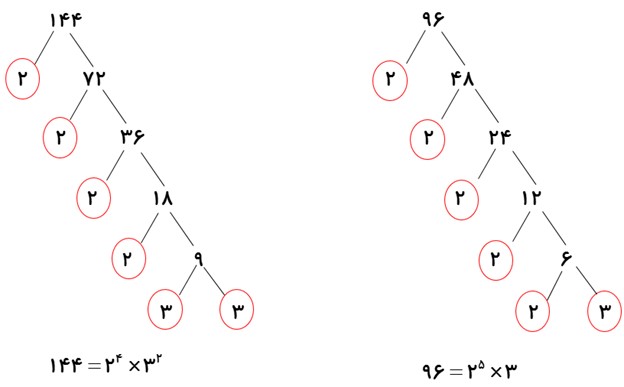
\(\left. \begin{array}{l}144 = {2^4} \times {3^2}\\\\96 = {2^5} \times 3\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\left( {144\,,\,96} \right) = {2^4} \times 3 = 48\\\\\left[ {144\,,\,96} \right] = {2^5} \times {3^2} = 288\end{array} \right.\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

مهم ترین کاربرد شمارنده های اول

فصل 5 : شمارنده ها و اعداد اول

ساده کردن کسرها

از مهم ترین کاربرد شمارنده های اول، ساده کردن کسرها می باشد. برای این منظور صورت و مخرج کسر را به شمارنده های اول آن تجزیه و سپس شمارنده های مشترک در صورت و مخرج را حذف می کنیم؛ مانند:

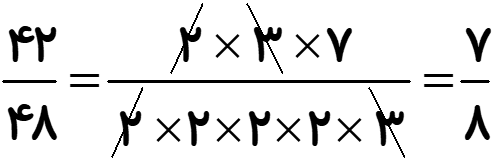
هم مخرج کردن کسرها

یکی از مهم ترین کاربردهای ک.م.م در پیدا کردن مخرج مشترک دو کسر است، یعنی کوچک ترین عددی را پیدا می کنیم که به هر دو مخرج بخش پذیر (قابل قسمت) باشد؛ مانند:

\(\begin{array}{l}\frac{{15}}{{12}} - \frac{7}{{18}} = \\18 = 2 \times 3 \times 3\\12 = 2 \times 2 \times 3\\\left[ {18\,,\,12} \right] = 2 \times 2 \times 3 \times 3 = 36\\\frac{{15}}{{12}} - \frac{7}{{18}} = \frac{{45}}{{36}} - \frac{{14}}{{36}} = \frac{{31}}{{36}}\end{array}\)

نکاتی درباره ب.م.م و ک.م.م

فصل 5 : شمارنده ها و اعداد اول

1 ب.م.م هر عدد با ۱، 1 می شود.

\(\left( {9\,,\,1} \right) = 1 \)

2 ک.م.م هر عدد با ۱، خود عدد می شود.

\(\left[ {1\,,\,12} \right] = 12\)

3 ب. م. م هر عدد با خودش، همان عدد می شود.

\(\left( {15\,,\,15} \right) = 15\)

4 ک.م.م هر عدد با خودش خود همان عدد می شود.

\(\left[ {7\,,\,7} \right] = 7\)

5 ب.م.م دو عدد اول ۱ می شود.

\(\left( {5\,,\,11} \right) = 1\)

6 ک.م.م دو عدد اول، حاصل ضرب آنها می شود.

\(\left[ {7\,,\,13} \right] = 91\)

7 ب. م. م دو عدد بخش پذیر عدد کوچکتر می شود.

\(\left( {7\,,\,35} \right) = 7\)

8 ک.م.م دو عدد بخش پذیر، عدد بزرگتر می شود.

\(\left[ {36\,,\,12} \right] = 36\)

9 ب.م.م دو عدد متوالی، ۱ می شود.

\(\left( {5\,,\,6} \right) = 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {18\,,\,19} \right) = 1\)

10 ک.م.م دو عدد متوالی، حاصل ضرب آنها می شود.

\(\left[ {8\,,\,9} \right] = 72\)

مثال

اگر a بر b بخش پذیر باشد، حاصل عبارت \(\left[ {\left( {ab\,,\,a} \right),\left( {ab\,,\,b} \right)} \right]\) را بیابید.

هرگاه a بر b بخش پذیر باشد، آنگاه a مضربی از b و همچنین b مقسوم علیه a خواهد بود؛ بنابراین:

\(\begin{array}{l}\left( {ab\,,\,a} \right) = a\\\\\left( {ab\,,\,b} \right) = b\\\\ \Rightarrow \left[ {\left( {ab\,,\,a} \right),\left( {ab\,,\,b} \right)} \right] = \left[ {a,b} \right] = a\end{array}\)

اگر \(\left[ {a\,,\,b} \right] = 36\,,\,\left( {a\,,\,b} \right) = 6\,,\,b > a\) و 30 = b + a باشد، حاصل b – a3 را بیابید.

از آنجایی که \(\left( {a\,,\,b} \right) = 6\) در نتیجه a و b مضربی از عدد 6 خواهند بود. همچنین چون مجموع آن دو برابر عدد 30 می شود، پس کوچکتر از عدد 30 خواهند بود؛ یعنی از اعداد 6، 12، 18 و 24 خواهند بود.

همچنین چون \(\left[ {a\,,\,b} \right] = 36\) می شود، بنابراین جزو اعداد 12 و 18 می باشند؛ در نتیجه:

\(\left. \begin{array}{l}\left( {a\,,\,b} \right) = 6 = 2 \times 3\\\\\left[ {a\,,\,b} \right] = 36 = {2^2} \times {3^2}\\\\a > b\\\\a + b = 30\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}a = 12\\\\b = 18\end{array} \right.\)

بنابراین حاصل عبارت خواسته شده برابر است با:

\(3a - b = 3 \times 12 - 18 = 18\)

اگر \(\left[ {a\,,\,b} \right] = a \times b\) و \(\frac{b}{a} = \frac{{144}}{{96}}\) ، حاصل عبارت b + a2 را بیابید.

هنگامی که ک.م.م دو عدد برابر حاصل ضرب یک دیگر هستند، در نتیجه نسبت به یکدیگر اول هستند. بنابراین اگر کسر داده شده را ساده کنیم، مقادیر مجهول را پیدا کرده ایم:

\(\begin{array}{l}\frac{b}{a} = \frac{{144}}{{96}} = \frac{3}{2} \Rightarrow \left\{ \begin{array}{l}a = 2\\\\b = 3\end{array} \right.\\\\ \Rightarrow 2a + b = 2 \times 2 + 3 = 7\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

حجم و انواع آن

فصل 6 : سطح و حجم

حجم

مقدار جایی که هر جسم در فضا اشغال می کند.

انواع حجم:

حجم ها را می توان به دو دسته هندسی و غیرهندسی تقسیم کرد. حجم های هندسی شکل های مشخص و تعریف دارند. حجم های هندسی را می توان به سه دسته تقسیم کرد:

1) منشوری

2) کروی

3) هرمی

برخی از حجم های هندسی نیز ترکیبی از این سه نوع اند.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

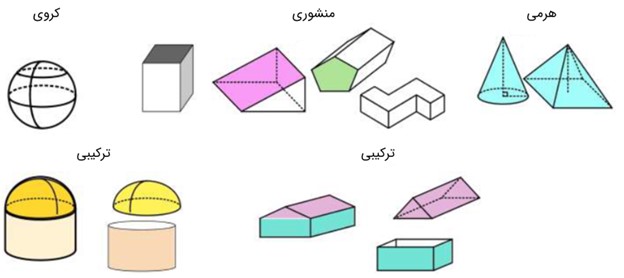
آشنایی بیشتر با حجم های منشوری

فصل 6 : سطح و حجم

آشنایی بیشتر با حجم های منشوری

حجم های منشوری بین دو صفحه موازی قرار می گیرند. به این دو سطح موازی که سطح منشوری را قطع می کنند، «قاعده» و به سطح های اطراف آن «وجه های جانبی» می گویند.

به محل برخورد سطح ها، «یال» و به نقطه برخورد هر سه سطح «رأس» می گویند.

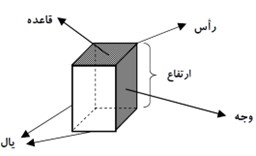
قاعده:

دو سطح بالا و پایین منشور.

وجه یا پهلو:

سطح های اطراف منشور.

یال:

محل برخورد هر دو وجه.

رأس:

محل برخورد یال ها.

ارتفاع:

فاصلۀ بین دو قاعده.

تعداد وجه ها یا پهلوها در حجم های منشوری:

۲ + تعداد ضلع های قاعده = تعداد وجه ها

تعداد یال ها در حجم های منشوری:

۳ × تعداد ضلع های قاعده = تعداد یال ها

تعداد رأس ها در حجم های منشوری:

2 × تعداد ضلع های قاعده = تعداد رأس ها

مقطع زدن:

برش زدن حجم های منشوری از ارتفاع آنها.

مثال

تعداد یال های یک مکعب مستطیل چند تا از تعداد رأس های آن بیشتر است؟

هر مکعب که مکعب مستطیل هم جزو آن دسته به شمار می آید، دارای 6 وجه، 12 یال، 8 رأس و 4 وجه جانبی است. بنابراین تعداد یال ها از تعداد رأس ها 4 عدد بیشتر است.

با 2000 مکعب کوچک، بزرگترین مکعب ممکن را ساخته ایم. چند مکعب کوچک اضافه آمده اند؟

بزرگ ترین مکعب ممکن را به کمک حدس و آزمایش بدست می آوریم:

\(\begin{array}{l}{10^3} = 1000\\{11^3} = 1331\\{12^3} = 1728\\{13^3} = 2197\end{array}\)

پس بزرگ ترین مکعب از 1728 مکعب کوچک ساخته می شود. بنابراین:

272 = 1728 – 2000 = تعداد اضافه مانده معکب های کوچک

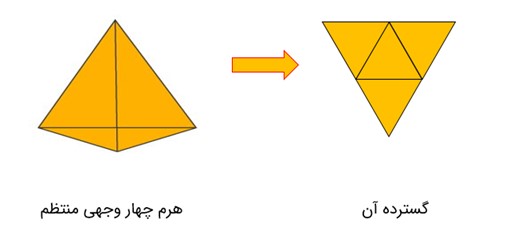
گسترده یک هرم چهار وجهی منتظم به چه صورت است؟

هرم چهار وجهی منتظم نوعی هرم است که از وجه های مثلث متساوی الاضلاع تشکیل شده است. بنابراین گسترده آن در شکل زیر آمده است:

تعداد وجه ها، رأس ها و یال های یک منشور که قاعده 5 ضلعی منتظم دارد را بدست آورید.

یک منشور که قاعده 5 ضلعی منتظم دارد در شکل زیر آمده است:

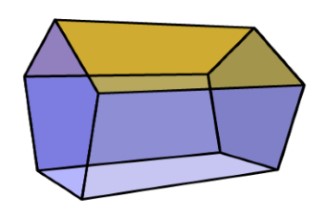
7 = 2 + 5= 2 + تعداد ضلع های قاعده = تعداد وجه ها

15 = 3 × 5 = 3 × تعداد ضلع های قاعده = تعداد یال ها

10 = 2 × 5 = 2 × تعداد ضلع های قاعده = تعداد رأس ها

جهت های دیدن یک حجم

فصل 6 : سطح و حجم

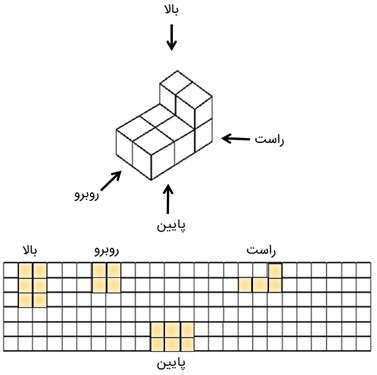
یک حجم را می توان از چهار جهت بالا، روبرو، راست و پایین مشاهده و آن را روی کاغذ شطرنجی رسم کرد؛ مانند:

مثال

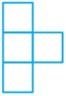
با توجه به زاویه دید شکل مقابل، حجم مقابل به چه شکلی دیده می شود؟

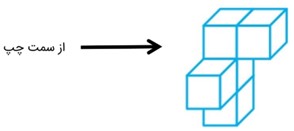
به صورت زیر دیده می شود:

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

محاسبه حجم منشورها

فصل 6 : سطح و حجم

تمام حجم های منشورها را می توانید از دستور زیر محاسبه کنید:

ارتفاع × مساحت قاعده = حجم منشور

رابطه جبری آن:

V = s.h

استوانه هم از حجم های منشوری حساب می شود که دارای قاعده دایره شکل می باشد.

واحدهای اندازه گیری حجم عبارتند از سانتیمتر مکعب و یا مترمکعب.

مثال

درون استوانه ای به شعاع 15 و ارتفاع 12، سوراخی به شعاع 5 ایجاد می کنیم. حجم شکل حاصل را بیابید.

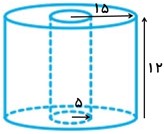
\( = \pi \times {15^2} \times 12 = 2700\pi \) حجم کل

\( = \pi \times {5^2} \times 12 = 300\pi \) حجم سوراخ

\( = 2700\pi - 300\pi = 2400\pi \) حجم شکل حاصل

درون مستطیلی به ابعاد 10 و 7 و ارتفاع 12، یک حفره استوانه ای شکل به شعاع قاعده 2 ایجاد می کنیم. اگر 3 = π ، حجم شکل حاصل را بیابید.

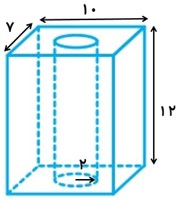
\( = 7 \times 10 \times 12 = 840\) حجم کل

\( = \pi \times {2^2} \times 12 = 48\pi = 48 \times 3 = 144\) حجم حفره

\( = 840 - 144 = 696\) حجم شکل حاصل

اگر شکل زیر را از قسمت نقطه چین تا بزنیم، یک جعبه به شکل مکعب مستطیل بدست می آید. حجم جعبه را بیابید.

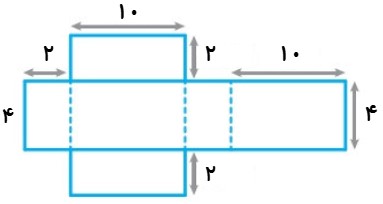
اگر به شکل دقت کنید، متوجه می شوید که:

2 = ارتفاع ، 4 = عرض ، 10 = طول

\( = 10 \times 4 \times 2 = 80\) حجم

اگر به ابعاد طول، عرض و ارتفاع مکعبی 20% اضافه کنیم، به حجم آن چند درصد اضافه می شود؟

اگر ابعاد مکعب را a در نظر بگیریم، داریم:

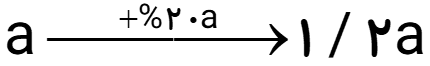
\( = 1/2 \times 1/2 \times 1/2 = 1/728\) حجم

\( \Rightarrow 1/728 - 1 = 0/728 = \% 72/8\)

به حجم مکعب 8/72 درصد اضافه می شود.

حجم شکل مقابل را به دست آورید. (3 = π)

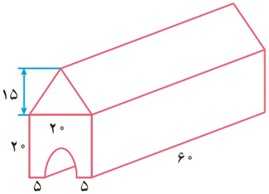
ارتفاع × مساحت قاعده = حجم

مساحت نیم دایره – مساحت مربع + مساحت مثلث = مساحت قاعده

\( = \frac{{20 \times 15}}{2} = 150\) مساحت مثلث

\( = 20 \times 20 = 400\) مساحت مربع

\( = \frac{{\pi \times {5^2}}}{2} = 12/5\pi = 12/5 \times 3 = 37/5\) مساحت نیم دایره

\( = \frac{{\pi \times {5^2}}}{2} = 150 + 400 - 37/5 = 512/5\) مساحت قاعده

\( = 512/5 \times 60 = 30750\) حجم

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

مساحت های جانبی و کل

فصل 6 : سطح و حجم

مساحت جانبی

به مجموع مساحت همه وجه های جانبی منشور مساحت جانبی آن می گویند. برای یافتن مساحت جانبی تمام منشورها می توانید از دستور زیر آن را محاسبه نمایید:

ارتفاع × محیط قاعده = مساحت جانبی

رابطه جبری آن:

S = P.h

قبل از رسیدن به مساحت کل درباره گسترده یا همان پهن شده حجم های منشوری شناخت بیشتری بیابیم. در زیر گسترده بعضی از این احجام را ملاحظه می نمایید:

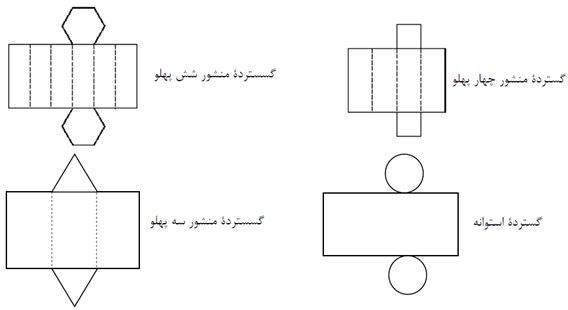
مساحت کل

به مجموع مساحت جانبی و مساحت دو قاعده تمامی منشورها، مساحت کل آن می گویند. برای یافتن مساحت کل تمام منشورها می توانید از دستور زیر آن را محاسبه نمایید:

مساحت دو قاعده + مساحت جانبی = مساحت کل

رابطه جبری آن:

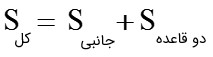
مثال

حجم یک مکعب \(27{a^3}\) است. مساحت جانبی آن کدام است؟

اگر x را ضلع مکعب در نظر بگیریم داریم:

\(27{a^3} = {x^3} \Rightarrow {3^3} \times {a^3} = {x^3} \Rightarrow {\left( {3a} \right)^3} = {x^3} \Rightarrow x = 3a\)

\( = 4{x^2} = 4{(3a)^2} = 4 \times 9{a^2} = 36{a^2}\) مساحت جانبی مکعب

نسبت حجم به مساحت کل یک مکعب به ضلع a را بیابید.

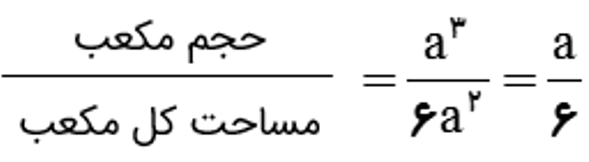
حجم و مساحت کل منشور روبرو را بدست آورید.

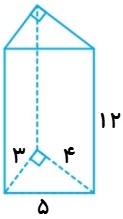
\( = (\frac{{3 \times 4}}{2}) \times 12 = 6 \times 12 = 72\) ارتفاع × مساحت قاعده = حجم

(مساحت قاعده × 2) + (ارتفاع × محیط قاعده) = مساحت کل

\(\begin{array}{l} = \left( {(3 + 4 + 5) \times 12} \right) + \left( {2 \times (\frac{{3 \times 4}}{2})} \right)\\ = 144 + 12 = 156\end{array}\)

اگر حجم یک مکعب، ربع مساحت کل آن باشد، مساحت جانبی آن چقدر است؟

ضلع مکعب را x فرض می کنیم؛ داریم:

\({x^3} = \frac{1}{4} \times 6{x^2} \Rightarrow x = \frac{6}{4} = \frac{3}{2}\)

\( = 4{x^2} = 4 \times \frac{3}{2} \times \frac{3}{2} = 9\) مساحت جانبی

حجم و سطح

فصل 6 : سطح و حجم

یک مستطیل با طول و عرض مشخص را به دو صورت زیر لوله می کنیم تا استوانه به دست آید.

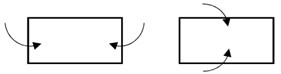
در هر حالت حجم استوانه ها را که به دست آوریم، مشاهده می کنیم این دو حجم با هم متفاوتند و این در حالی است که هر دو حجم از مستطیلی یک اندازه حاصل شده اند.

پس می توان نتیجه گرفت با حرکت یک سطح در فضا حجم ساخته می شود که احجام حاصل با هم متفاوتند. از این خاصیت در خراطی، تراشکاری و سفالگری برای ساختن حجم های مختلف استفاده می کنند.

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

تعریف توان

فصل 7 : توان و جذر

تعریف توان

عبارتی مانند ۲ × ۲ × ۲ × ۲ × ۲ را در ریاضیات برای ساده تر شدن به صورت 2⁵ می نویسیم و آن را چنین می خوانیم:

۲ به توان 5

در عبارت ۲⁵، ۲ را پایه و ۵ را توان می نامیم، درست شبیه همان کاری که در ساده کردن و خلاصه کردن جمع انجام می دادیم:

۲+۲+۲+۲+۲ = ۲×۵

نکاتی درباره توان

1) از توان به منظور مختصر نویسی ضرب های تکراری یک عدد استفاده می کنند.

2) به توان، «نما» و «قوّه» هم گفته می شود.

3) هر عدد به توان یک برابر خودش می شود:

\({a^1} = a\)

4) عدد یک به توان هر عددی برابر یک می شود:

\({1^{53}} = 1\)

5) هر عدد به توان صفر، ۱ می شود:

\({12^ \circ } = 1\)

6) عدد صفر به توان هر عدد مثبتی برابر صفر می شود:

\({ \circ ^{15}} = \circ \)

7) صفر به توان صفر تعریف نشده است:

\({ \circ ^ \circ } = \) تعریف نشده

مثال

حاصل عبارات زیر را بدست آورید.

\(\begin{array}{l}1)\,{10^ \circ }\;\;\;\;\;\;\;2){1^7}\;\;\;\;\;\;\;3){ \circ ^4}\;\;\;\;\;\;\;4){5^1}\\\\5){( - 6)^2}\,\,\,\,\,6) - {3^3}\,\,\,\,7){( - 2)^ \circ }\,\,\,\,\,\,8)( - 3) \times ( - 3) \times ( - 3)\\\\9){11^2}\,\,\,\,\,\,\,\,\,\,10){6^1}\,\,\,\,\,\,\,\,\,\,11){ \circ ^1}\,\,\,\,\,\,\,\,\,\,\,12){( - 2)^ \circ } \times {2^5}\end{array}\)

\(\begin{array}{l}1)\,{10^ \circ } = 1\;\;\;\;\;\;\;\\\\2){1^7} = 7\;\\\\3){ \circ ^4} = \; \circ \\\\4){5^1} = 5\\\\5){( - 6)^2} = \,( - 6) \times ( - 6) = 36\\\\6) - {3^3} = - (3 \times 3 \times 3) = - 27\\\\7){( - 2)^ \circ } = 1\\\,\,\\8)( - 3) \times ( - 3) \times ( - 3) = {( - 3)^2} = - 27\\\\9){11^2} = 11 \times 11 = 121\,\,\,\,\,\\\\10){6^1} = 6\\\\11){ \circ ^1} = \circ \\\\12){( - 2)^ \circ } \times {2^5} = 1 \times 2 \times 2 \times 2 \times 2 \times 2 = 32\end{array}\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

پرانتز در اعداد توان دار

فصل 7 : توان و جذر

نقش پرانتز در اعداد توان دار

1) اگر عددی منفی داخل پرانتز به توان زوج رسید، حاصل عددی مثبت می شود:

\({( - 3)^2} = ( - 3) \times ( - 3) = + 9\)

2) اگر توان عددی منفی داخل پرانتز بود، پرانتز در توان رساندن عدد نقشی ندارد:

\(( - {3^2}) = - (3 \times 3) = - 9\)

3) اگر عددی منفی بدون پرانتز به توان برسد، حاصل عددی منفی می شود:

\( - {4^2} = - (4 \times 4) = - 16\)

4) اگر یک کسر داخل پرانتز به توان برسد، توان شامل صورت و مخرج (هر دو) می شود:

\({(\frac{2}{3})^3} = \frac{{2 \times 2 \times 2}}{{3 \times 3 \times 3}} = \frac{8}{{27}}\)

5) اگر کسری داخل پرانتز به توان گرفت یا توان در صورت یا مخرج کسر باشد، پرانتز هیچ نقشی در توان ندارد:

\(\begin{array}{l}(\frac{{{2^3}}}{5}) = \frac{{2 \times 2 \times 2}}{5} = \frac{8}{5}\\\\\frac{7}{{{3^3}}} = \frac{7}{{3 \times 3 \times 3}} = \frac{7}{{27}}\end{array}\)

6) اگر یک عبارت جبری داخل پرانتز به توان برسد، توان شامل تک تک جمله های عبارت می شود:

\({(2ab)^3} = {2^3}{a^3}{b^3} = 8{a^3}{b^3}\)

7) اگر جمله ای از یک عبارت جبری توان نداشت، توانش ۱ می باشد:

\(5{a^2}b{x^8} = 5{a^2}{b^1}{x^8}\)

مثال

حاصل عبارات زیر را بدست آورید.

\(\begin{array}{l}1)\,{( - 1)^4}\;\;\;\;\;\;\;2){( - 1)^3}\;\;\;\;\;\;\;3)( - {3^4})\;\;\;\;\;\;\;4) - {5^2}\\\\5)\frac{4}{{{3^2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6)\frac{{{{( - 4)}^2}}}{{{4^2}}}\,\,\,\,\,\,\,7){( - \frac{2}{5})^2}\,\,\,\,\,\,\,\,\,\,8){(\frac{a}{b})^3}\end{array}\)

\(\begin{array}{l}1)\,{( - 1)^4} = 1\\\\2){( - 1)^3} = - 1\\\\3)( - {3^4}) = - (3 \times 3 \times 3 \times 3) = - 81\\\\4) - {5^2} = - (5 \times 5) = - 25\\\\5)\frac{4}{{{3^2}}} = \frac{4}{{3 \times 3}} = \frac{4}{9}\\\\6)\frac{{{{( - 4)}^2}}}{{{4^2}}} = \frac{{( - 4) \times ( - 4)}}{{4 \times 4}} = \frac{{16}}{{16}} = 1\\\\7){( - \frac{2}{5})^2} = ( - \frac{2}{5}) \times ( - \frac{2}{5}) = \frac{4}{{25}}\\\\8){(\frac{a}{b})^3} = \frac{a}{b} \times \frac{a}{b} \times \frac{a}{b} = \frac{{a \times a \times a}}{{b \times b \times b}} = \frac{{{a^3}}}{{{b^3}}}\end{array}\)

محاسبه عبارت توان دار

فصل 7 : توان و جذر

محاسبه عبارت توان دار

با توجه به درس توان، ترتیب انجام دادن عملیات مختلف ریاضی به صورت زیر انجام می شود:

۱) پرانتز

2) توان

3) ضرب و تقسیم

۴) جمع و تفریق

\(\frac{{{4^3} \times 4 + 9 - 6}}{{{5^2} + {2^3}}} = \frac{{64 \times 4 + 3}}{{25 + 8}} = \frac{{259}}{{33}}\)

گسترده توانی یک عدد

در نوشتن گسترده توانی هر عدد، ارزش مکانی رقم ها را به صورت توانی از ۱۰ می نویسیم:

\(\begin{array}{l}5062 = 5000 + 60 + 2\\\,\,\,\,\,\,\,\,\,{\rm{ }}\,\, = 5 \times {10^3} + \circ \times {10^2} + 6 \times {10^1} + 2 \times {10^ \circ }\end{array}\)

مثال

حاصل عبارت زیر را به دست آورید.

\(\frac{{{5^3} - {3^3}}}{{{5^3} + {3^3}}} = \)

\(\frac{{{5^3} - {3^3}}}{{{5^3} + {3^3}}} = \frac{{125 - 27}}{{125 + 27}} = \frac{{98}}{{152}} = \frac{{49}}{{76}}\)

مثال

گستره توانی عدد های 58906 و 40200 رابنویسید.

\(\begin{array}{l}58906 = 50000 + 8000 + 900 + 6\\\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 5 \times {10^4} + 8 \times {10^3} + 9 \times {10^2} + \circ \times {10^1} + 6 \times {10^ \circ }\\\\40200 = 40000 + 200\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 4 \times {10^4} + \circ \times {10^3} + 2 \times {10^2} + \circ \times {10^1} + \circ \times {10^ \circ }\\\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

ساده کردن عبارت توان دار

فصل 7 : توان و جذر

ساده کردن عبارت های توان دار

۱) در ضرب عددهای توان دار با پایه های مساوی یکی از پایه ها را نوشته و توان ها را جمع می کنیم:

\({\left( { - 3} \right)^2} \times {\left( { - 3} \right)^4} = {\left( { - 3} \right)^{2 + 4}} = {\left( { - 3} \right)^6}\)

2) در ضرب عددهای توان دار با توان های مساوی، پایه ها را در هم ضرب و یکی از توان ها را می نویسیم:

\({5^4} \times {\left( { - 3} \right)^4} = {\left( {5 \times ( - 3)} \right)^4} = {\left( { - 15} \right)^4}\)

3) اگر ظاهر پایه ها مثل هم نبود، مثلاً یکی عدد و دیگری کسر بود، سعی می کنیم آنها به یک شکل تبدیل کنیم:

\(\begin{array}{l}{(\frac{1}{2})^3} \times {(0/5)^6} = ?\\0/5 = \frac{5}{{10}} = \frac{1}{2}\\{(\frac{1}{2})^3} \times {(0/5)^6} = {(\frac{1}{2})^3} \times {(\frac{1}{2})^6} = {(\frac{1}{2})^{3 + 6}} = {(\frac{1}{2})^9}\end{array}\)

4) یک عدد توان دار را در صورت نیاز می توان به صورت ضرب دو یا چند عدد توان دار تبدیل کرد:

\(\begin{array}{l}{3^7} = {3^2} \times 3 \times {3^4}\\{15^4} = {3^4} \times {5^4}\end{array}\)

این خواص کمک به حل بسیاری از سوالات اعداد توان دار می نماید.

مثال

اگر \({2^{10}} = 1024\) باشد، حاصل 2¹² را به دست آورید.

\({2^{12}} = {2^{10}} \times {2^2} = 1024 \times 4 = 4096\)

مثال

باز شده عدد توان دار زیر را بنویسید.

\({12^7} = ?\)

\(\begin{array}{l}{12^7} = ?\\{12^7} = {(2 \times 6)^7} = {2^7} \times {6^7}\end{array}\)

عبارت توان دار زیر را ساده کنید.

\({5^2} \times {5^7} \times {7^9} = ?\)

\(\begin{array}{l}{5^2} \times {5^7} \times {7^9} = ?\\\underline {{5^2} \times {5^7}} \times {7^9} = {5^{2 + 7}} \times {7^9} = {5^9} \times {7^9} = {(5 \times 7)^9}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {35^9}\end{array}\)

پیش بینی ارقام یک عدد توان دار

مثال

اگر \({4^5} = 1024\) باشد، عدد\({4^{10}}\)چند رقمی است ؟

\({4^{10}} = {4^5} \times {4^5}\)

اگر\({4^5}\)را ۱۰۰۰ فرض کنیم، پس داریم:

\(1000 \times 1000 = 1,000,000\)

در نتیجه\({4^{10}}\)هفت رقمی خواهد بود.

1 استثنای تفریق اعداد توان دار:

\(\begin{array}{l}{10^2} - {6^2} = {4^3}\\{21^2} - {15^2} = {6^3}\end{array}\)

2 استثنای جمع اعداد توان دار:

\({3^9} + {3^9} + {3^9} = {3^9} \times 3 = {3^{10}}\)

محاسبه عبارت توان دار به کمک مقدار داده شده

مثال

اگر \({2^a} = 7\) باشد، مقدار \({2^{a + 1}}\) را بدست آورید.

\({2^{a + 1}} = {2^a} \times {2^1} = 7 \times 2 = 14\)

مثال

حاصل عبارات توان دار زیر را حل کنید.

\(\begin{array}{l}1)\, - {(1 - 2(1 - 2(1 - 2(1 - {2^{ - 1}}))))^{ - 1}}\\\\2)\,\frac{{{4^{a + 2}} - {4^{a + 1}} - {4^a}}}{{{2^a} + {2^a} + {2^a} + {2^a}}}\\\\3)\,\frac{{{2^{101}} + {2^{100}} + {2^{99}} \cdots + {2^{60}}}}{{{2^{51}} + {2^{100}} + {2^{99}} \cdots + {2^{10}}}}\\\\4)\,\frac{{{3^{2a + 2}} \div {3^{2a - 2}}}}{{{9^{2b + 2}} \times {9^{ - 2b}}}}\end{array}\)

1 فقط به اولویت عملیاتی دقت کنید:

\(\begin{array}{l} - {(1 - 2(1 - 2(1 - 2(1 - {2^{ - 1}}))))^{ - 1}}\mathop = \limits^{{2^{ - 1}} = \frac{1}{2}} \\\\ - {(1 - 2(1 - 2(1 - 2(1 - \frac{1}{2}))))^{ - 1}} = \\\\ - {(1 - 2(1 - 2(1 - 2(\frac{1}{2}))))^{ - 1}} = \\\\ - {(1 - 2(1 - 2(1 - 0)))^{ - 1}} = \\\\ - {(1 - 2(1 - 2))^{ - 1}} = \\\\ - {(1 - 2( - 1))^{ - 1}} = - {(1 + 2)^{ - 1}} = - {(3)^{ - 1}} = - \frac{1}{3}\end{array}\)

\(\begin{array}{l}\frac{{{4^{a + 2}} - {4^{a + 1}} - {4^a}}}{{{2^a} + {2^a} + {2^a} + {2^a}}} = \frac{{{4^a}({4^2} - 4 - 1)}}{{{2^a} \times 4}} = \\\\\frac{{{4^a}}}{{{2^a}}} \times \frac{{11}}{4} = {(\frac{4}{2})^a} \times \frac{{11}}{4} = {2^a} \times \frac{{11}}{4}\end{array}\)

\(\begin{array}{l}\,\frac{{{2^{101}} + {2^{100}} + {2^{99}} \cdots + {2^{60}}}}{{{2^{61}} + {2^{60}} + {2^{59}} \cdots + {2^{10}}}} = \\\\\frac{{{2^{60}}({2^{51}} + {2^{50}} + {2^{49}} \cdots + 2 + 1)}}{{{2^{10}}({2^{51}} + {2^{50}} + {2^{49}} \cdots + 2 + 1)}} = \frac{{{2^{60}}}}{{{2^{10}}}} = {2^{60 - 10}} = {2^{50}}\\\end{array}\)

\(\,\frac{{{3^{2a + 2}} \div {3^{2a - 2}}}}{{{9^{2b + 2}} \times {9^{ - 2b}}}} = \frac{{{3^{(2a + 2) - (2a - 2)}}}}{{{9^{(2b + 2 + ( - 2b))}}}} = \frac{{{3^4}}}{{{9^2}}} = \frac{{81}}{{81}} = 1\)

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

جذر(ریشه دوم)

فصل 7 : توان و جذر

جذر(ریشه دوم)

هر گاه عددی در خودش ضرب شود، این حاصل را مجذور و به عددی که در خوش ضرب شده جذر می گوییم. هر عدد مثبت دارای دو ریشه، یکی مثبت و دیگری منفی می باش . مانند عدد ۲۵ که دو ریشه ۵+ و ۵- را دارد.

1 به ریشه دوم مثبت هر عدد جذر آن عدد گفته می شود.

2 علامت جذر \(\sqrt {} \) است .

3 جذر هر عدد برابر است با دو عدد که قرینه یکدیگرند.

4 به جذر یک عدد ریشه دوم آن نیز گفته می شود.

5 اعداد منفی جذر ندارند. زیرا حاصل ضرب هیچ عددی در خوش، منفی نمی شود. عدد صفر تنها یک ریشه دارد که آن خود عدد صفر است.

انواع جذر

1- جذر کامل:

اعداد طبیعی که جذر کامل دارند، یعنی جذر آنها یک عدد طبیعی می شود را مجذور کامل گویند؛ مانند 1، 4، 9، 16، 25 و … . برای رسیدن به جذر کامل از خود سوال کنید چه عددی در خوش ضرب شده که عدد زیر رادیکال را تشکیل داده است؟ مانند:

\(\sqrt {49} = 7\)

2- جذر تقریبی:

جذرهایی که یک عدد اعشاری شوند. برای رسیدن به جذر تقریبی یک عدد، ابتدا باید معلوم کنید که عدد زیر رادیکال شما بین کدام دو عدد صحیح قرار گرفته است؛ مانند \(\sqrt {18} \) که بین دو رایکال \(\sqrt {16} \) و \(\sqrt {25} \) قرار گرفته یعنی \(\sqrt {16} < \sqrt {18} < \sqrt {25} \) بین دو عدد ۴ و 5 قرار گرفته است. این فاصله را نصف کرده به توان ۲ برسانید.

می توانید اگر به عدد کوچکتر نزدیک بود، 1/0 - 1/0 به عدد کوچکتر اضافه کنید تا به حدود جذر مورد نظر برسید و اگر به عدد بزرگتر نزدیک بود، 1/0 - 1/0 از عدد بزرگتر کم کنید تا به حدود جذر مورد نظر برسید.

پس داریم:

\(\sqrt {18} \simeq 4/2\)

مثال

حاصل عبارت هایی که جذر کامل دارند را بنویسید.

\(\begin{array}{l}1)\,\sqrt {49} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\sqrt {0/25} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3)\,\sqrt {8/1} \\\\4)\,\sqrt {8 \times 2} \,\,\,\,\,\,\,\,\,\,\,5)\,\sqrt 3 \times \sqrt {27} \,\,\,\,\,\,\,\,\,\,\,\,6)\,\sqrt 1 \\\\7)\sqrt {125} \,\,\,\,\,\,\,\,\,\,\,\,\,\,8)\sqrt {169} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9)\,\sqrt {\frac{{10}}{{0/1}}} \end{array}\)

\(\begin{array}{l}1)\,\sqrt {49} = 7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\sqrt {0/25} = 0/5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\3)\,\sqrt {8/1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4)\,\sqrt {8 \times 2} \, = \sqrt {16} = 4\\\\5)\,\sqrt 3 \times \sqrt {27} = \sqrt {3 \times 27} = \sqrt {81} = 9\\\\6)\,\sqrt {1\,} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7)\sqrt {125} \,\\\\8)\sqrt {169} = 13\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9)\,\sqrt {\frac{{10}}{{0/1}}} = \sqrt {10 \times 10} = 10\end{array}\)

مثال

حاصل عبارت زیر را حساب کنید.

\(\sqrt {\sqrt {\sqrt {\sqrt {{{81}^2}} } } } \)

\(\sqrt {\sqrt {\sqrt {\sqrt {{{81}^2}} } } } = \sqrt {\sqrt {\sqrt {81} } } = \sqrt {\sqrt 9 } = \sqrt 3 \)

مثال

حاصل عبارات زیر را بدست آورید.

\(\begin{array}{l}1)\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {\sqrt {2\sqrt 4 } } } } } } } } \\\\2)\sqrt {\frac{{25}}{{16}}} + \sqrt {\frac{9}{{25}}} - \sqrt {\frac{{16}}{9}} \end{array}\)

\(\begin{array}{l}1)\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt 4 } } } } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt 4 } } } } } } = \sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } = \sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } = \\\sqrt {2\sqrt {2\sqrt {2 \times 2} } } = \sqrt {2\sqrt {2 \times 2} } = \sqrt {2 \times 2} = 2\\\\2)\sqrt {\frac{{25}}{{16}}} + \sqrt {\frac{9}{{25}}} - \sqrt {\frac{{16}}{9}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} + \frac{{\sqrt 9 }}{{\sqrt {25} }} - \frac{{\sqrt {16} }}{{\sqrt 9 }} = \\\frac{5}{4} + \frac{3}{5} - \frac{4}{3} = \frac{{75 + 36 - 80}}{{60}} = \frac{{31}}{{60}}\end{array}\)

بردار

فصل 8 : بردار و مختصات

شناخت بردار

حرکت و نیرو را با پاره خط های جهت دار نشان می دهیم.در ریاضی به پاره خط جهت دار بردار می گوییم. بردار OA را به صورت \(\overrightarrow {OA} \) نشان می دهیم.

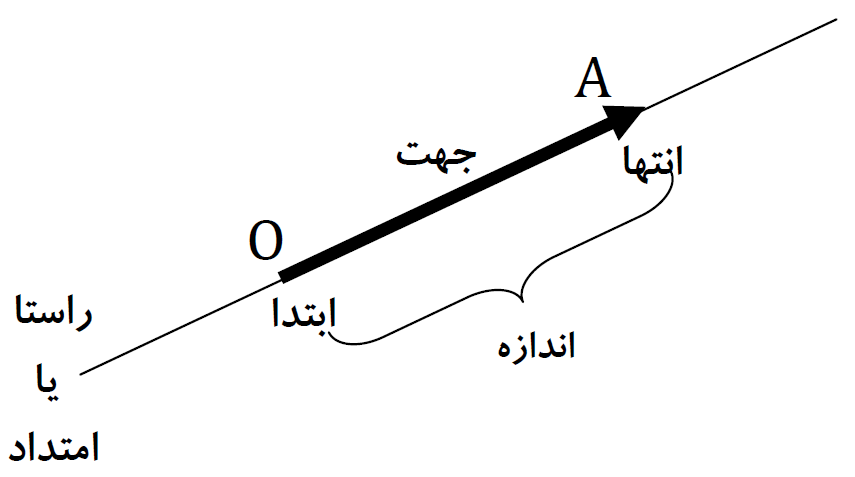
نام گذاری بردار

این کار به دو صورت انجام می شود:

الف) نخست نقطه ابتدا، سپس نقطه انتها را نوشته و نماد → را روی آن قرار دهید؛ مانند: \(\overrightarrow {AB} \)

\(A\;\; \to \;\;B\)

ب) با یک حرف کوچک لاتین که در وسط بردار قرار می گیرد، انجام می شود؛ مانند:

تهیه کننده:مسعود زیرکاری

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

اندازه و انواع بردارها

فصل 8 : بردار و مختصات

اندازه (طول) بردار

برای رسیدن به اندازه بردار نخست به جهت حرکت بردار توجه نمایید (سمت راست + و سمت چپ -) و سپس تعداد واحد های بین ابتدا و انتهای بردار را بشمارید.

بردارهای مساوی

دو بردار وقتی برابرند که هم راستا هم اندازه و هم جهت باشند.

بردارهای قرینه

دو بردار وقتی قرینه یکدیگرند که مساوی باشند، اما در خلاف جهت هم حرکت کنند؛ مانند:

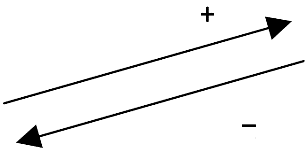
جمع دو بردار قرینه، همیشه صفر می شود.

تهیه کننده:مسعود زیرکاری

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

مختصات

فصل 8 : بردار و مختصات

مختصات

از دو محور عمود بر هم تشکیل می شود. محور افقی را محور طول ها (x ها) و محور عمودی را محور عرض ها (y ها) می نامند.

محل برخورد دو محور را «مبدأ مختصات» می نامند و با حرف O نمایش می دهند.

محورهای مختصات صفحه را به ۴ قسمت تقسیم می کنند.

در شکل مقابل این ۴ ناحیه با عددهای ۱ تا ۴ مشخص شده اند.

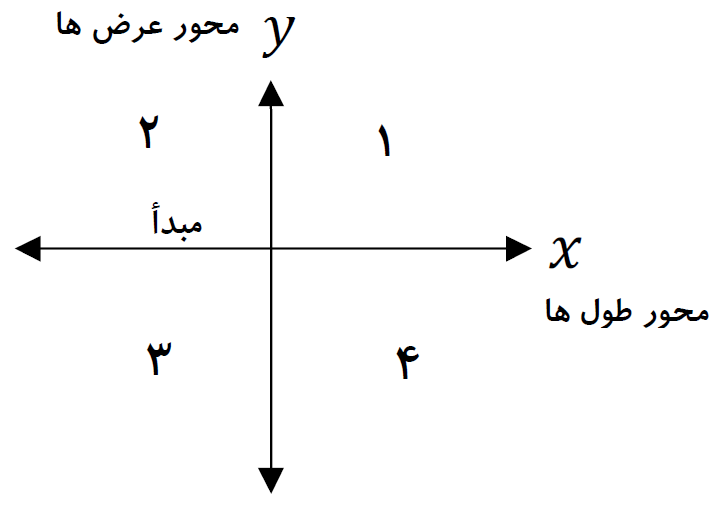
مختصات نقطه

به طول و عرض هر نقطه که به صورت \(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\) نمایش داده می شود، مختصات آن نقطه گفته می شود.

این مختصات می تواند + ، - یا حتی 0 باشد.

مختصات نقاط در ٤ قسمت:

1) اگر نقطه ای در قسمت ۱ (ربع یا ناحیه اول) قرار گرفته باشد، دارای طول و عرض مثبت می باشد:

\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& + \\y& + \end{array}} \right]\)قسمت 1

2) اگر نقطه در قسمت ۲ (ربع یا ناحیه دوم) قرار گرفته باشد، دارای طول منفی و عرض مثبت می باشد:

\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& - \\y& + \end{array}} \right]\)قسمت 2

3) اگر نقطه در قسمت ۳ (ربع یا ناحیه سوم) قرار گرفته باشد، دارای طول و عرض منفی می باشد:

\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& - \\y& - \end{array}} \right]\)قسمت 3

4) و اگر نقطه در قسمت ۴ (ربع یا ناحیه چهارم) قرار گرفته باشد، دارای طول مثبت و عرض منفی می باشد:

\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& + \\y& - \end{array}} \right]\)قسمت 4

اگر نقطه ای روی محور طولها (x ها) قرار گرفته باشد، طول آن نقطه عدد و عرض آن 0 می شود.

1 تمام بردارهایی که موازی محور x ها باشند نیز دارای عرض 0 می باشند.

2 اگر نقطه ای روی محور عرض ها (y ها) قرار گرفته باشد، طول آن نقطه 0 و عرض آن عدد می شود.

3 تمام بردارهایی که موازی محور y ها باشند نیز دارای طول 0 می باشند.

مختصات مبدأ مختصات

محل برخورد محورهای مختصات را با حرف O نمایش می دهند و مختصات آن برابر است با: \(O = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\)

مثال

ناحیه نقاط زیر را بنویسد.

\(\begin{array}{l}1)\,\left[ {\begin{array}{*{20}{c}}1\\{ - 1}\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\left[ {\begin{array}{*{20}{c}}{ - 5}\\{ - 4/5}\end{array}} \right]\\\\3)\left[ \begin{array}{l}6\\5\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4)\left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\\\\5)\,\left[ {\begin{array}{*{20}{c}}{ - 1}\\1\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6)\left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right]\\\\7)\,\left[ {\begin{array}{*{20}{c}} \circ \\6\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8)\left[ {\begin{array}{*{20}{c}}5\\5\end{array}} \right]\end{array}\)

1 ناحیه چهارم 2 ناحیه سوم 3 ناحیه اول

4 مرکز مختصات 5 ناحیه دوم 6 محور x های منفی

7 محور y های مثبت 8 ناحیه اول (بر روی نیم ساز ناحیه اول و سوم)

مثال

اگر نقطه \(\left[ {\begin{array}{*{20}{c}}{m + 6}\\{ - 3m - 5}\end{array}} \right]\) روی محور y ها باشد، مختصات نقطه را مشخص کنید.

هنگامی که مختصات نقطه ای بر روی محور y ها باشد، مؤلفه x آن برابر صفر خواهد بود:

\(m + 6 = 0 \Rightarrow m = - 6 \Rightarrow \left[ {\begin{array}{*{20}{c}} \circ \\{13}\end{array}} \right]\)

مثال

اگر فاصله نقطه \(\left[ {\begin{array}{*{20}{c}}{ - 4a + 1}\\{3a + 8}\end{array}} \right]\) از هر دو محور مختصات به یک فاصله باشد، مختصات نقطه را بیابید و ناحیه آن را مشخص کنید.

\(\begin{array}{l} - 4a + 1 = 3a + 8 \Rightarrow - 4a - 3a = 8 - 1\\\\ \Rightarrow - 7a = 7 \Rightarrow a = - 1 \Rightarrow \left[ \begin{array}{l}5\\5\end{array} \right]\end{array}\)

نقطه در ناحیه اول قرار دارد.

تهیه کننده: مسعود زیرکاری

اعمال ریاضی در بردارها

فصل 8 : بردار و مختصات

جمع متناظر بردار

در نوشتن جمع متناظر با یک بردار به مقدار ابتدا، اندازه و انتهای آن نیاز دارید تا با استفاده از دستور زیر بتوانید جمع متناظر بردار را بنویسید:

انتها = اندازه + ابتدا

بردار انتقال

به برداری گفته می شود که یک نقطه یا یک شکل را به اندازه مختصاتش (از ابتدا به انتها) منتقل نماید.

قرینه بردار

قرینه ابتدا و انتهای بردار مورد نظر را نسبت به مبدأ مختصات یا یکی از محورها (طول یا عرض) یافته و سپس بردار قرینه را رسم می کنیم.

قرینه بردار نسبت به محور طول ها

فقط عرض بردار قرینه می شود:

\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;x \to \;\left[ {\begin{array}{*{20}{c}}x\\{ - y}\end{array}} \right]\)

قرینه بردار نسبت به محور عض ها

فقط طول بردار قرینه می شود:

\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;y \to \;\left[ {\begin{array}{*{20}{c}}x\\{ - y}\end{array}} \right]\)

قرینه بردار نسبت به مبدأ مختصات

طول و عرض بردار هر دو قرینه می شود:

\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;o \to \;\;\left[ {\begin{array}{*{20}{c}}{ - x}\\{ - y}\end{array}} \right]\)

مثال

مرکز پاره خط AB که در آن \(A = \left[ \begin{array}{l}5\\4\end{array} \right]\) و \(B = \left[ \begin{array}{l} - 3\\6\end{array} \right]\) را بیابید.

\(\begin{array}{l}\left. \begin{array}{l}A = \left[ \begin{array}{l}5\\4\end{array} \right] = \left[ \begin{array}{l}{x_A}\\{y_A}\end{array} \right]\\\\B = \left[ \begin{array}{l} - 3\\6\end{array} \right] = \left[ \begin{array}{l}{x_B}\\{y_B}\end{array} \right]\end{array} \right\} \Rightarrow M = \left[ \begin{array}{l}{x_M}\\{y_M}\end{array} \right]\\\\\left. \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{5 + ( - 3)}}{2} = \frac{2}{2} = 1\\\\{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{6 + 4}}{2} = \frac{{10}}{2} = 5\end{array} \right\} \Rightarrow M = \left[ \begin{array}{l}1\\5\end{array} \right]\end{array}\)

مثال

بردار \(\left[ \begin{array}{l}9 - 3x\\1 - \frac{y}{3}\end{array} \right]\) برداری است که ابتدا و انتهای آن روی هم قرار دارند؛ y + x را بدست آورید.

فقط بردار \(\overrightarrow O = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\) ابتدا و انتهای آن روی هم قرار دارند؛ بنابراین:

\(\begin{array}{l}\left[ \begin{array}{l}9 - 3x\\1 - \frac{y}{3}\end{array} \right] = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right] \Rightarrow \left\{ \begin{array}{l}9 - 3x = 0 \Rightarrow 9 = 3x \Rightarrow x = 3\\\\1 - \frac{y}{3} = 0 \Rightarrow 1 = \frac{y}{3} \Rightarrow y = 3\end{array} \right.\\\\ \Rightarrow x + y = 6\end{array}\)

مثال

قرینه بردارهای زیر را نسبت به مرکز و یا محور داده شده مشخص کنید.

\(\begin{array}{l}1)\,\,\left[ \begin{array}{l} - 2\\4\end{array} \right]\,\,\,\,\,\,\,\,\,\,y \to \\\\2)\,\,\left[ \begin{array}{l}5\\ - 3\end{array} \right]\,\,\,\,\,\,\,\,\,\,x \to \\\\3)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,y \to \\\\4)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,x \to \\\\5)\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \\\\6)\,\,\left[ \begin{array}{l} - 10\\ + 3\end{array} \right]\,\,\,\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \end{array}\)

\(\begin{array}{l}1)\,\,\left[ \begin{array}{l} - 2\\4\end{array} \right]\,\,\,\,\,\,y \to \,\,\,\,\,\,\left[ \begin{array}{l}2\\4\end{array} \right]\\\\2)\,\,\left[ \begin{array}{l}5\\ - 3\end{array} \right]\,\,\,\,\,\,\,x \to \,\,\,\,\left[ \begin{array}{l}5\\3\end{array} \right]\\\\3)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,y \to \,\,\,\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\\\\4)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,x \to \,\,\,\,\,\left[ \begin{array}{l} - 15\\20\end{array} \right]\\\\5)\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \,\,\,\,\left[ \begin{array}{l} - 15\\20\end{array} \right]\\\\6)\,\,\left[ \begin{array}{l} - 10\\ + 3\end{array} \right]\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \,\,\,\,\left[ \begin{array}{l} + 10\\ - 3\end{array} \right]\end{array}\)

تهیه کننده: مسعود زیرکاری

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

یافتن مقدار مجهول در تساوی های برداری

فصل 8 : بردار و مختصات

یافتن مقدار مجهول در تساوی های برداری

اگر مقدار مجهول (نامعلوم) در انتهای تساوی برداری بود، مقدارهای ابتدا و اندازه را با هم جمع کنید؛ مانند:

\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}2\\{ - 4}\end{array}} \right]\;\; + \left[ {\begin{array}{*{20}{c}}{ - 3}\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\\\\\left. \begin{array}{l}x = 2 + ( - 3) = - 1\\y = ( - 4) + 1 = - 3\end{array} \right\}\;\; \Rightarrow \;\;\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 3}\end{array}} \right]\end{array}\)

اگر مقدار مجهول (نامعلوم) در ابتدا یا اندازه تساوی برداری قرار گرفته بود، مقدار انتها را منهای قسمت دیگر کنید:

\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}2\\{ - y}\end{array}} \right]\;\; + \left[ {\begin{array}{*{20}{c}}{ - x}\\{ - 2}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 2}\\3\end{array}} \right]\\\\\left. \begin{array}{l} - x = ( - 2) - 2 = - 4\\ - y = 3 - ( - 2) = 5\end{array} \right\}\; \Rightarrow \,\,\left. \begin{array}{l}x = 4\\y = - 5\end{array} \right\}\,\, \Rightarrow \;\;\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}4\\{ - 5}\end{array}} \right]\end{array}\)

مثال

اگر \(A = \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right]\,\,,\,\,B = \left[ {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right]\) و \(2\overrightarrow {BA} + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right]\) ، مختصات نقطه C را بدست آورید.

ابتدا بردار \(\overrightarrow {AC} \) را بدست می آوریم:

\(\begin{array}{l}\overrightarrow {BA} = \overrightarrow {OA} - \overrightarrow {OB} = \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 2}\\2\end{array}} \right]\\\\2\overrightarrow {BA} + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] \Rightarrow 2\left[ {\begin{array}{*{20}{c}}{ - 2}\\2\end{array}} \right] + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right]\\\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{ - 4}\\4\end{array}} \right] + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] \Rightarrow \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}{ - 4}\\4\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right]\\\\\overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} \Rightarrow \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right] = \overrightarrow {OC} - \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right]\\\\ \Rightarrow \overrightarrow {OC} = \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right] \Rightarrow \overrightarrow {OC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\3\end{array}} \right] \Rightarrow C = \left[ {\begin{array}{*{20}{c}}{ - 5}\\3\end{array}} \right]\end{array}\)

مثال

اگر \(\left[ {\begin{array}{*{20}{c}}{4x + 3}\\{7 + y}\end{array}} \right]\, = \left[ {\begin{array}{*{20}{c}}{x - 3}\\{10 - 2y}\end{array}} \right]\) ، حاصل \(\frac{{3x - 1}}{{4y + 2}}\) کدام است؟

\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{4x + 3}\\{7 + y}\end{array}} \right]\, = \left[ {\begin{array}{*{20}{c}}{x - 3}\\{10 - 2y}\end{array}} \right]\\\\4x + 3 = x - 3 \Rightarrow 3x = - 3 \Rightarrow x = - 1\\\\7 + y = 10 - 2y \Rightarrow 3y = - 3 \Rightarrow y = - 1\\\\ \Rightarrow \frac{{3x - 1}}{{4y + 2}} = \frac{{3( - 1) - 1}}{{4( - 1) + 2}} = \frac{{ - 4}}{{ - 2}} = 2\end{array}\)

تهیه کننده:مسعود زیرکاری

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

تعیین مختصات بردار به کمک ترسیم

فصل 8 : بردار و مختصات

تعیین مختصات بردار به کمک ترسیم

از ابتدا و انتهای بردار، دو خط به موازات محور طول و عرض به ترتیب رسم کنید تا در نقطه ای یکدیگر را قطع کنند و تشکیل یک مثلث قائم الزاویه دهند. حالا از ابتدا به سمت انتهای بردار حرکت کنید تا هم جهت و هم مختصات آن را مشخص کنید؛ مانند:

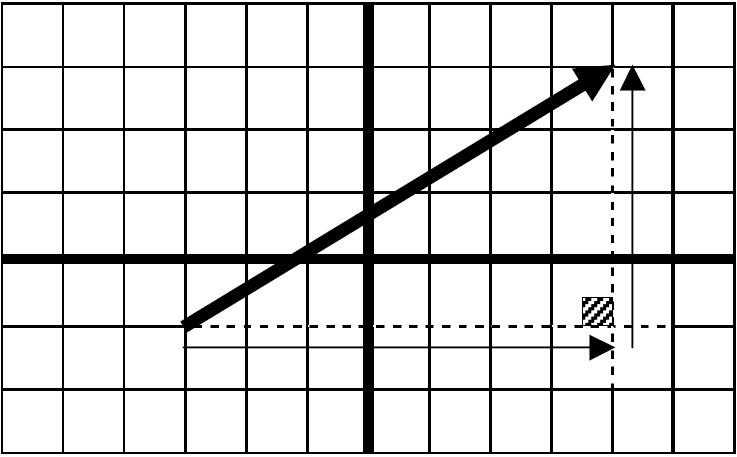
می بینید از ابتدای بردار ۷ واحد به سمت راست حرکت کرده ایم، یعنی ۷+ و 4+ واحد نیز به سمت بالا حرکت کرده ایم؛ پس مختصات بردار مورد نظر \(\left[ {\begin{array}{*{20}{c}}{ + 7}\\{ + 4}\end{array}} \right]\) خواهد بود.

مثال

بردار خواسته شده را رسم کنید.

1 بردار \(\left[ {\begin{array}{*{20}{c}}{ - 2}\\{ - 1}\end{array}} \right]\) ابتدا در \(\left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 2}\end{array}} \right]\)

2 بردار \(\left[ {\begin{array}{*{20}{c}}2\\{ - 2}\end{array}} \right]\) انتها در \(\left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\)

3 بردار \(\left[ {\begin{array}{*{20}{c}}3\\{ - 4}\end{array}} \right]\) ابتدا در \(\left[ {\begin{array}{*{20}{c}}{ - 4}\\2\end{array}} \right]\)

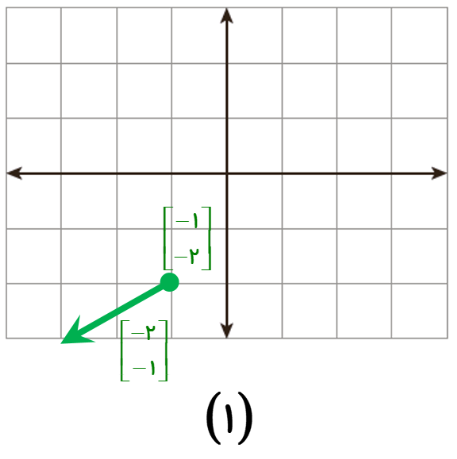
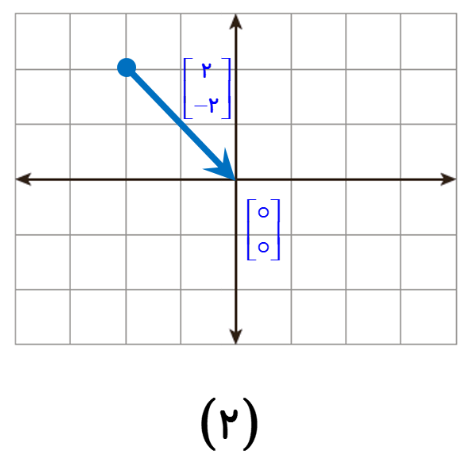
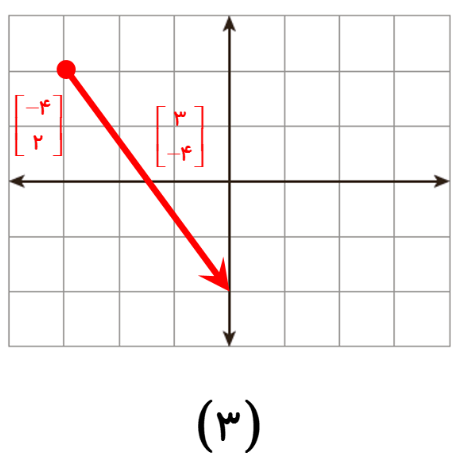
تهیه کننده:مسعود زیرکاری

انواع نمودار در علم آمار

فصل 9 : آمار و احتمال

علم آمار

علم آمار علم جمع آوری اطلاعات، سازماندهی و بررسی آنها است. اطلاعات، جمع آوری شده را «داده های آماری» می گویند.

نمودار در علم آمار

برای مقایسه و بررسی بهتر داده های آماری از انواع «نمودارها» استفاده می کنند. هر نمودار با توجه به موضوعی که داده های آن جمع آوری شده است و نوع اطلاعات به دست آمده، کارایی دارد.

انواع نمودارها و تفسیر نتیجه ها

1- نمودار میله ای:

نمودار میله ای برای مقایسه تعداد پیدا کردن بیشترین و کمترین داده به کار می رود.

در حال حاضر نرم افزارهای زیادی برای رسم انواع نمودار ها وجود دارند.

آنچه اهمیت دارد رسم نمودار نیست، بلکه انتخاب نمودار مناسب برای موضوع مورد نظر است.

مثال

مدت زمانی که طول می کشد تا کارگران یک کار خانه از خانه به محل کار بروند، در نمودار مقابل نشان داده شده است. با توجه به این نمودار، فاصله زمانی خانۀ چند کارگر تا محل کار بیشتر از 10 دقیقه است؟

ابتدا ستون هایی را مشخص می کنیم که زمان بیشتر از 10 دقیقه را نشان می دهند (ستون های سوم، چهارم و پنجم):

45 نفر : ستون سوم (11 تا 15 دقیقه)

30 نفر : ستون چهارم (16 تا 20 دقیقه)

5 نفر : ستون پنجم (20 تا 25 دقیقه)

نفر 80 = 5 + 30 + 45 = تعداد کارگرانی که فاصله خانه تا محل کار بیشتر از 10 دقیقه است

2- نمودار خط شکسته:

نمودار خط شکسته برای نمایش تغییرها کاربرد دارد؛ بنابراین در موضوع هایی که تغییرها اهمیت دارد، از این نمودار استفاده می شود.

برای نمونه، تغییرها در بازارهای مالی، قیمت طلا، نفت، سهام و ... را با این نمودار نشان می دهند.

گاهی وقت ها به جای داده های واقعی از مقدار تقریبی آنها استفاده می کنیم. در برنامه ریزی های کلان به عددهای واقعی و دقیق نیاز نداریم.

برای مثال مقدار تولید گندم یک استان را به صورت چند هزار تن بیان می کنند؛ یعنی مقدار کمتر از ۱۰۰۰ تن یا یک میلیون کیلوگرم در این بررسی اهمیت ندارد.

مثال

در نمودار خط شکسته زیر، بیشترین تغییرات دما بین کدام یک از ماه های سال است؟

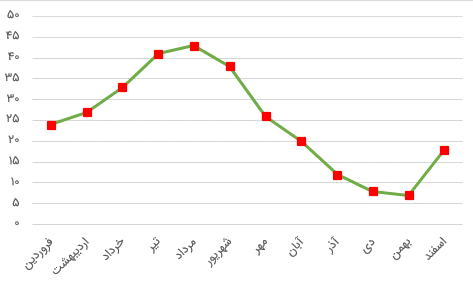
در نمودار خط شکسته، وقتی شیب خطی بیشتر باشد، یعنی تغییرات در آن قسمت ها بیشتر از بقیه قسمت هاست. در نمودار بالا بین دو ماه شهریور و مهر و دو ماه بهمن و اسفند تغییرات دمایی بالایی است؛ حال بین این دو تغییرات یکی از تغییرات بیشترین خواهد بود:

10 = 7 – 17 = تغییرات دمایی بین دو ماه شهریور و مهر

13 = 25 – 38 = تغییرات دمایی بین دو ماه بهمن و اسفند

3- نمودار دایره ای:

بعضی از داده ها و اطلاعات جمع آوری شده نشان می دهد که یک مقدار مشخص به چه نسبتی به بخش های کوچک تر تقسیم شده است.

در این موارد می توان تقسیم شدن را روی یک شکل مثل دایره نشان داد و سهم هر بخش را روی دایره مشخص کرد.

در نمودار دایره ای به طور معمول نسبت و سهم هر بخش را به صورت درصد محاسبه کرده و سپس روی نمودار نمایش می دهند.

مثال

نمودار دایره ای مقابل مربوط به محصولات یک مزرعه است. اگر میزان کل محصولات 180 تن باشد، میزان محصولات این مزرعه را مشخص کنید.

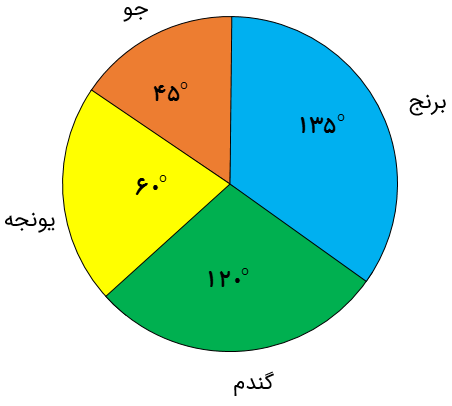
تن \(\, = \,\frac{{{{135}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 67/5\) میزان برنج

تن\(\, = \,\frac{{{{45}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 22/5\) میزان جو

تن\(\, = \,\frac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 30\) میزان یونجه

میزان گندم\(\, = \,\frac{{{{120}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 60\)تن

4- نمودار تصویری:

گاهی وقت ها به جای داده های واقعی از مقدار تقریبی آنها استفاده می کنیم. در برنامه ریزی های کلان به عدد های واقعی و دقیق نیاز نداریم؛ برای مثال مقدار تولید گندم یک استان را به صورت چند هزار تن بیان می کنند، یعنی مقدار کمتر از ۱۰۰۰ تن یا یک میلیون کیلوگرم در این بررسی اهمیت ندارد.

ابتدا مقدار تقریبی هر عدد را با تقریب کمتر از مقدار مورد نظر گرد کنید. سپس با رسم یک شکل برای تعدادی مشخص، نمودار تصویری آن را رسم کنید.

مثال

اگر هر شکل سیب کامل رو به عنوان 10 عدد سیب در نظر بگیریم، و فردی میزان فروش سیب را در ماه های اسفند تا خرداد به صورت زیر ثبت کرده باشد، نمودار تصویری این برنامه فروش را رسم کنید.

در اسفند، 10 سیب فروخته شد.

در فروردین، 40 سیب فروخته شد.

در اردیبهشت 25 سیب فروخته شد.

در خرداد 20 سیب فروخته شد.

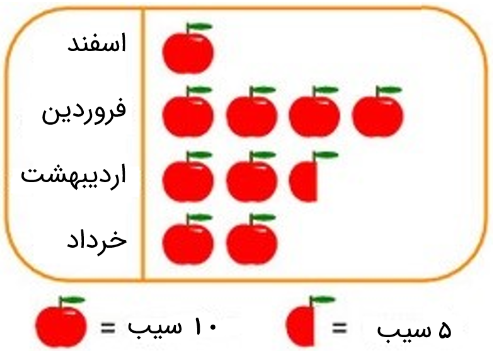
تهیه کننده: مسعود زیرکاری

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

دسته بندی داده ها (فراوانی،میانگین)

فصل 9 : آمار و احتمال

دسته بندی داده ها

اگر داده های جمع آوری شده زیاد و پراکنده باشند بررسی آنها طولانی می شود. برای اینکه بتوانیم آسان تر و بهتر نتیجه بگیریم، داده ها را متناسب با موضوع آماری دسته بندی و سازماندهی می کنیم.

دامنه تغییرات در داده های آماری

به فاصله بین کمترین و بیشترین داده، «دامنه تغییرات» می گویند.

مثال

دامنه تغییرات داده های آماری زیر را بیابید.

10، 15، 13، 21، 18، 23، 8، 1، 30، 31، 15، 10، 8، 7، 12، 11

ابتدا کمترین داده و بیشترین داده را مشخص می کنیم:

1 = کمترین داده

31 = بیشترین داده

30 = 1 – 31 = دامنه تغییرات

فراوانی

تعداد داده های هر دسته را «فراوانی» می گویند. فراوانی را به دو صورت زیر می توان نشان داد:

۱) استفاده از چوب خط

۲) استفاده از عدد

مثال

جدول زیر، امتیازهای شرکت کنندگان یک آزمون 100 نمره ای را نشان می دهد. ابتدا ستون فراوانی را بر اساس ستون چوب خط کامل کنید؛ سپس محاسبه کنید که امتیاز چند نفر بیشتر از 60 می باشد.

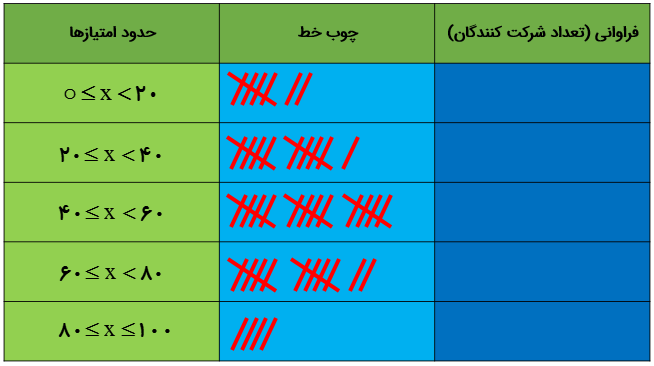
16 = 4 + 12 = تعداد شرکت کنندگانی که امتیاز بالای 60 گرفته اند

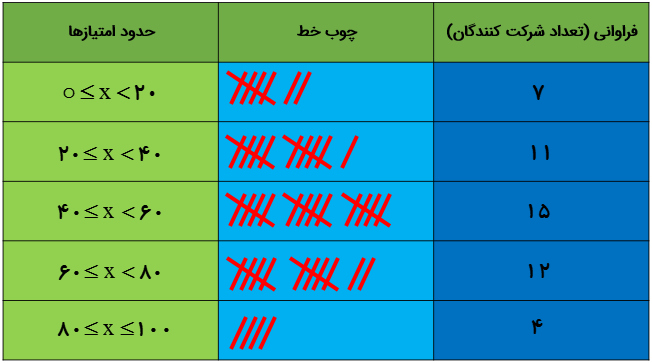
میانگین داده ها

پس از اینکه داده های آماری در جدول سازماندهی می شوند و به کمک نمودارها درک بهتری از داده ها به دست آمد، می توان از میانگین داده ها برای کامل تر شدن نتایج حاصل از داده ها و تحلیل و تفسیر بهتر آنها استفاده کرد. میانگین تعدادی داده از تقسیم مجموع آنها بر تعدادشان به دست می آید:

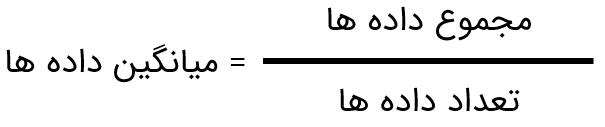
به صورت جبری:

\(\overline x = \frac{s}{n}\)

اگر تعداد داده ها زیاد باشد و داده ها دسته بندی شده باشند، می توان میانگین داده ها را با تقریب بسیار خوب به دست آورد.

مثال

اگر نمودار تغییرات دمایی یک منطقه در 24 ساعت در نمودار زیر آمده باشد، میانگین دمایی این منطقه را بدست آورید.

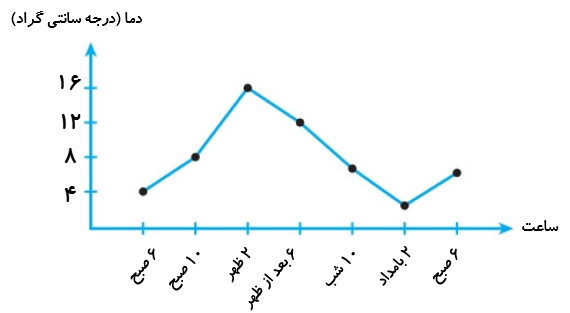
همه دماهای مشخص شده را جمع می بندیم و بر تعداد نقطه ها تقسیم می کنیم:

میانگین دمای منطقه\(\,\, = \frac{{4 + 8 + 16 + 12 + 8 + 4 + 8}}{7} = \frac{{60}}{7} \simeq 8/6\)درجه سانتی گراد

تهیه کننده: مسعود زیرکاری

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم

جزوه جامع علوم تجربی هفتم

جزوه جامع مطالعات اجتماعی هفتم

جزوه جامع عربی هفتم

جزوه جامع فارسی هفتم

جزوه جامع نگارش هفتم

جزوه جامع زبان انگلیسی هفتم

جزوه جامع کتاب کار انگلیسی هفتم

جزوه جامع پیام های آسمانی هفتم

جزوه جامع آموزش قرآن هفتم

جزوه جامع کار و فناوری هفتم

جزوه جامع تفکر و سبک زندگی هفتم

جزوه جامع تربیت دینی هفتم

احتمال یا اندازه گیری شانس

فصل 9 : آمار و احتمال

احتمال یا اندازه گیری شانس

وقتی یک سکه را می اندازیم دو حالت هم شانس ممکن است اتفاق بیفتد، یا سکه رو می آید یا پشت و چون در یک حالت از این دو حالت ممکن، سکه رو می آید، پس احتمال رو آمدن سکه \(\frac{1}{2}\) است.

به این ترتیب برای بیان اندازه شانس رخ دادن یک اتفاق، از یک عدد استفاده کرده ایم که «احتمال رخ دادن» آن اتفاق نامیده می شود.

برای اینکه احتمال رخ دادن یک اتفاق را به دست آوریم، ابتدا همۀ حالت های ممکن را می یابیم، سپس حالت های مورد نظر را از میان حالت های ممکن پیدا می کنیم. احتمال رخ دادن اتفاق مورد نظر برابر است با نسبت تعداد حالت های مورد نظر به تعداد حالت های ممکن؛ بنابراین احتمال رخ دادن یک اتفاق از دستور زیر به دست خواهد آمد:

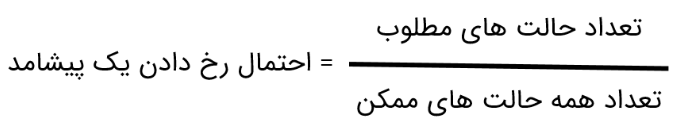
به عبارت دیگر برای اینکه احتمال رخ دادن یک پیشامد را بیابیم، تعداد حالت های منجر به آن اتفاق را بر تعداد کل حالت ها تقسیم می کنیم. احتمال روی دادن هر پیشامد را با یک کسر که بین صفر و یک می باشد، نشان می دهیم.

محاسبه n بار از انتظار یک پیشامد

از دستور زیر کمک می گیریم:

تعداد کل انجام کار × احتمال روی دادن اتفاق

مثال

تاسی را ۶۰ بار پرتاب می کنیم. انتظار داریم چند بار عدد ۴ بیاید؟

\(\frac{1}{6} \times 60 = 10\)

مثال

تمام پیشامدهای ممکن از پرتاب دو سکه را بنویسید.

رو آمدن سکه را با R و پشت آمدن آن را با P نشان می دهیم:

تمام پیشامدهای ممکن از پرتاب دو سکه\( = \left\{ {(R\,,\,R)\,,\,(R\,,\,P)\,,\,(P\,,\,R)\,,\,(P\,,\,P)} \right\}\)

(R ، P) یعنی اینکه سکه اول پشت بیاید و سکه دوم رو ظاهر شود.

مثال

احتمال رخ دادن پیشامد اینکه در پرتاب دو سکه، هر دو سکه پشت ظاهر شوند را بیابید.

پیشامد پشت ظاهر شدن دو سکه\(\,\, = \left\{ {(P\,,\,P)} \right\}\)

تمام پیشامدهای ممکن\(\,\, = \left\{ {(R\,,\,R)\,,\,(R\,,\,P)\,,\,(P\,,\,R)\,,\,(P\,,\,P)} \right\}\)

احتمال\( = \frac{1}{4}\)

مثال

یک سکه و یک تاس را هم زمان به آسمان پرتاب می کنیم. تمام پیشامدهای ممکن را نوشته و محاسبه کنید که چقدر احتمال دارد که بر روی تاس عدد زوج ظاهر شود و سکه نیز رو ظاهر شود؟

رو آمدن سکه را با R و پشت آمدن آن را با P نشان می دهیم:

تمام پیشامدهای ممکن\(\,\, = \left\{ \begin{array}{l}(R\,,\,1)\,,\,(R\,,\,2)\,,\,(R\,,\,3)\,,\,(R\,,\,4)\,,\,(R\,,\,5)\,,\,(R\,,\,6)\,,\,\\(P\,,\,1)\,,\,(P\,,\,2)\,,\,(P\,,\,3)\,,\,(P\,,\,4)\,,\,(P\,,\,5)\,,\,(P\,,\,6)\end{array} \right\}\)

تعداد تمام حالت های ممکن 12 می باشد.

پیشامد تاس زوج و سکه رو\(\,\, = \left\{ {(R\,,\,2)\,,\,(R\,,\,4)\,,\,(R\,,\,6)} \right\}\)

تعداد این پیشامد نیز 3 می باشد. در نتیجه:

احتمال\( = \frac{3}{{12}} = \frac{1}{4}\)

تهیه کننده:مسعود زیرکاری

روش های نوشتن کل حالات پیشامد

فصل 9 : آمار و احتمال

مجموع روی دادن و روی ندادن یک پیشامد

مجموع احتمال روی دادن و احتمال روی ندادن یک اتفاق همیشه برابر با عدد ۱ است.

روش های نوشتن کل حالت های یک پیشامد

برای این کار از دو روش زیر کمک می گیریم:

1- جدول نظام دار:

جدول نظام دار برای حالتی مناسب که دو رویداد را مورد بررسی قرار دهیم. در این روش حالت های یک رویداد را افقی و حالت های رویداد بعدی را عمودی نوشته و مانند جدول ضرب، سایر خانه ها را پر می کنیم.

۲- نمودار درختی:

در روش نمودار درختی، برای هر حالت یک شاخه در نظر گرفته و در انتهای هر شاخه حالت های پیشامد بعدی را می نویسیم. روش نمودار درختی می تواند بهترین روش برای محاسبه همه حالت های رخداد یک پیشامد باشد.

مثال

تمام پیشامدهای ممکن از پرتاب سه تا سکه را به صورت جدول نظام دار و نمودار درختی نمایش دهید.

نمایش به صورت جدول نظام دار:

جدول نظام دار
سکه اول	سکه دوم	سکه سوم
رو	رو	رو
رو	رو	پشت
رو	پشت	رو
رو	پشت	پشت
پشت	رو	رو
پشت	رو	پشت
پشت	پشت	رو
پشت	پشت	پشت

نمایش به صورت نمودار درختی:

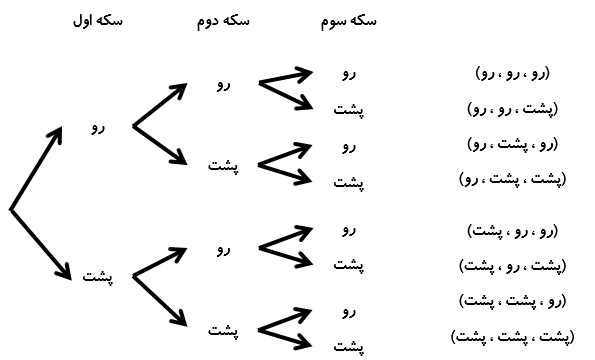
البته نوع دیگری از نمایش جدول نظام دار برای همین مثال به صورت زیر است:

جدول نظام دار
سکه اول	سکه دوم	سکه سوم
رو	رو	رو
		پشت
	پشت	رو
		پشت
پشت		رو
	رو	پشت
	پشت	رو
		پشت

مثال

تمام پیشامدهای ممکن از پرتاب یک سکه و یک تاس را به صورت جدول نظام دار و نمودار درختی نمایش دهید.

نمایش به صورت جدول نظام دار:

جدول نظام دار
تاس	سکه
1	رو
2
3
4
5
6
1	پشت
2
3
4
5
6

نمایش به صورت نمودار درختی:

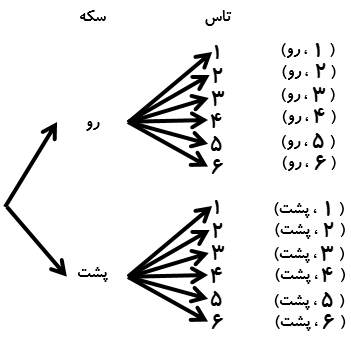
تهیه کننده:مسعود زیرکاری

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

محتوا مورد پسند بوده است ؟

2.65 - 96 رای

صفحه رسمی مای درس

گروه و کانال های تلگرام عصر

گام به گام تمام دروس

آموزش جامع

به وبسایت مای درس خوش آمدید

ویدئو های آموزشی

جزوات

نمونه سوالات

خلاصه نکات ریاضی هفتم - درسنامه شب امتحان ریاضی هفتم - جزوه شب امتحان ریاضی هفتم نوبت اول

راهبردهای حل مسئله

فصل 1 : راهبردهای حل مسئله

مراحل حل یک مسئله

1- فهمیدن مسئله

2- انتخاب راهبرد مناسب

راهبردهای حل مسئله

مای درس ، برترین اپلیکیشن کمک درسی ایران

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد الگوسازی (تفکّر نظام دار)

فصل 1 : راهبردهای حل مسئله

راهبرد الگوسازی

جزوات جامع پایه هفتم

راهبرد حذف حالت های نامطلوب

فصل 1 : راهبردهای حل مسئله

راهبرد حذف حالت های نامطلوب

راهبرد الگویابی

فصل 1 : راهبردهای حل مسئله

راهبرد الگویابی

مای درس ، برترین اپلیکیشن کمک درسی ایران

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد حدس و آزمایش

فصل 1 : راهبردهای حل مسئله

راهبرد حدس و آزمایش

جزوات جامع پایه هفتم

راهبرد زیر مسئله

فصل 1 : راهبردهای حل مسئله

راهبرد زیرمسئله

راهبرد حل مسئله ساده تر

فصل 1 : راهبردهای حل مسئله

راهبرد حل مسئله ساده تر

مای درس ، برترین اپلیکیشن کمک درسی ایران

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

راهبرد روش های نمادین

فصل 1 : راهبردهای حل مسئله

راهبرد روش های نمادین

جزوات جامع پایه هفتم

راهبرد رسم شکل

فصل 1 : راهبردهای حل مسئله

راهبرد رسم شکل

عددهای علامت دار

فصل 2 : عددهای صحیح

مای درس ، برترین اپلیکیشن کمک درسی ایران

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

قرینه اعداد صحیح

فصل 2 : عددهای صحیح

جزوات جامع پایه هفتم

حرکت روی محور عددهای صحیح

فصل 2 : عددهای صحیح

جمع عددهای صحیح روی محور

فصل 2 : عددهای صحیح

جمع و تفریق عددهای صحیح (بدون محور):

جمع و تفریق عددهای صحیح (به روش ارزش مکانی):

مای درس ، برترین اپلیکیشن کمک درسی ایران

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

ضرب عددهای صحیح به کمک محور

فصل 2 : عددهای صحیح

ضرب و تقسیم عددهای صحیح

عبارت های ترکیبی

جزوات جامع پایه هفتم