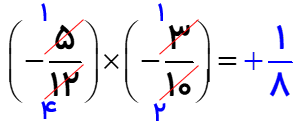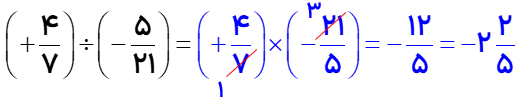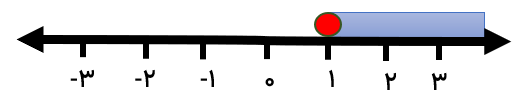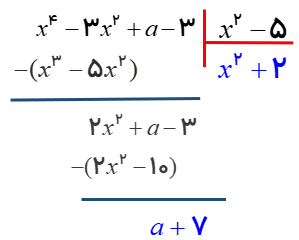درسنامه کامل ریاضی نهم
تعداد بازدید : 209.65kخلاصه نکات ریاضی نهم - درسنامه شب امتحان ریاضی نهم - جزوه شب امتحان ریاضی نهم نوبت اول
مجموعه
فصل 1 : مجموعه ها
مجموعه
به دسته ای از اشیاء کاملا مشخص و دو به دو متمایز (غیر تکراری) «مجموعه» می گویند.
مثال
کدام یک از عبارات زیر مشخص کننده یک مجموعه است؟
الف) 3 عدد زوج متوالی
مجموعه نیست
ب) 4 گل زیبا
مجموعه نیست
پ) اعداد اول کمتر از 10
مجموعه است
1 جموعه را به صورت آکولاد { } نشان می دهند و مجموعه را با حروف بزرگ انگلیسی نام گذاری می کنند.
2 به هر یک از اعداد و عبارت داخل مجموعه عضو می گویند و علامت عضو بودن به صورت \( \in \)و علامت عضو نبودن به صورت \( \notin \)می باشد.
3 تعداد عضو های هر مجموعه مانند A را به صورت n(A) نشان می دهند.
مثال
با توجه به مجموعه ی A درستی یا نادرستی هر عبارت را مشخص کنید.
\(A = \{ 3\,,\,\{ 4\,,\,5\} \,,\,6\} \)
\(n(A) = 4\)
نادرست
\(3 \in A\)
درست
\(4 \notin A\)
درست
\(\{ 6\} \in A\)
نادرست
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مجموعه تهی
فصل 1 : مجموعه ها
مجموعه تهی
مجموعه ای که دارای هیچ عضوی نباشد. علامت مجموعه تهی بصورت { } یا \(\emptyset \) می باشد.
مثال
کدام یک از مجموعه های زیر مجموعه تهی است؟
الف اعداد طبیعی کمتر از 4
\(\{ 1\,,\,2\,,\,3\} \)
ب عداد صحیح کمتر از صفر
\(\{ \ldots \,,\, - 3\,,\, - 2\,,\, - 1\} \)
پ اعداد طبیعی بین 4 و 5
\(\{ \} \)
مجموعه تهی است
تهیه کننده : مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
دو مجموعه برابر
فصل 1 : مجموعه ها
دو مجموعه برابر
دو مجموعه A و B را برابر می گویند که هر عضو مجموعه A در مجموعه B و هر عضو مجموعه B در مجموعه A وجود داشته باشد؛ مانند دو مجموعه ی مقابل:
\(B = \left\{ {\sqrt 9 ,7,\frac{{20}}{5}} \right\}\) و \(A = \{ 4,3,7\} \)
مثال
دو مجموعه ی زیر برابرند،مقدار x و y را به دست آورید؟
\(\left\{ {x - 7,3} \right\} = \left\{ {4,y} \right\}\)
\(\left\{ \begin{array}{l}x - 7 = 4 \Rightarrow x = 11\\\\y = 3\end{array} \right.\)
تهیه کننده : مسعود زیرکاری
زیر مجموعه
فصل 1 : مجموعه ها
زیر مجموعه
مجموعه A زیر مجموعه B است. هر گاه هر عضو مجموعه A عضوی از مجموعه B باشد و آن را به صورت \(A \subseteq B\) نشان می دهد. اگر A زیر مجموعه B نباشد آن را بصورت \(A \not\subset B\) نشان می دهند.
1 اگر \(A \subseteq B\) باشد آنگاه رابطه های زیر همواره برقرار است:
\(\left\{ \begin{array}{l}A \cup B = B\\\\A \cap B = A\end{array} \right.\)
2 برای پیدا کردن تعداد زیر مجموعه ها از رابطه \({2^n}\) استفاده می کنیم. اگر تعداد زیر مجموعه را داشته باشیم و تعداد عضو را خواسته باشند عدد داده شده را تجزیه می کنیم.
مثال
الف مجموعه ی \(A = \{ 1\,,\,2\,,\,3\,,\, \ldots \,,\,10\} \) چند زیر مجموعه دارد؟
\(n(A)\, = \,10\, \Rightarrow \,{2^n}\, = \,\,{2^n} = \,\,1024\,\) زیر مجموعه
ب یک مجموعه دارای 32 زیر مجموعه است. این مجموعه دارای چند عضو است؟
\(32\, = \,{2^5}\, \Rightarrow \,\) 5 عضو دارد
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نمایش مجموعه ها
فصل 1 : مجموعه ها
نمایش مجموعه ها
الف) مجموعه اعداد طبیعی: \(\mathbb{N} = \{ 1\,,\,2\,,\,3\,,\, \ldots \} \)
ب) مجموعه اعداد حسابی: \(W = \{ 0\,,\,1\,,\,2\,,\,3\,,\, \ldots \} \)
پ) مجموعه اعداد صحیح: \(\mathbb{Z} = \{ \ldots \,,\, - 3\,,\, - 2\,,\, - 1\,,\,0\,,\,1\,,\,2\,,\,3\,,\, \ldots \} \)
ت) مجموعه اعداد طبیعی زوج: \(E = \{ 2\,,\,4\,,\,6\,,\, \ldots \} \)
ث) مجموعه اعداد طبیعی فرد: \(O = \{ 1\,,\,3\,,\,5\,,\, \ldots \} \)
ج) مجموعه اعداد گویا: \(Q\, = \,\{ \frac{a}{b}\,|\,a\,,\,b\, \in \,\mathbb{Z}\,,\,b\, \ne \,0\} \)
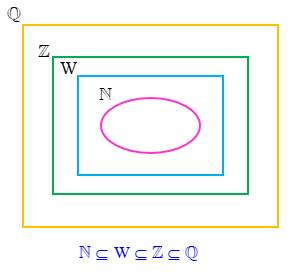
نمودار ون مجموعه ها
مجموعه ها را می توان داخل یک منحنی بسته ای نشان داد.
نمودار ون مجموعه اعداد ریاضی به صورت زیر است:
مثال
الف عضو های هر مجموعه را بنویسید:
\(A = \{ x|x \in \mathbb{Z}\,,\, - 4 \le x < 2\} \)
\(A = \{ - 4\,,\, - 3\,,\, - 2\,,\, - 1\,,\,0\,,\,1\} \)
\(B = \{ 2x - 1|x \in \mathbb{N}\,,\,x \le 3\} \)
\(B = \{ 2(1) - 1\,,\,2(2) - 1\,,\,2(3) - 1\} = \{ 1\,,\,3\,,\,5\} \)
ب صورت ریاضی هر مجموعه را بنویسید:
\(C = \{ 4\,,\,8\,,\,12\,,\, \ldots \} \)
\(C = \{ 4x|x \in \mathbb{N}\} \)
\(D = \{ - 6\,,\, - 5\,,\, - 4\,,\, \ldots \,,\,3\} \)
\(D = \{ x|x \in \mathbb{Z}\,,\, - 7 < x < 4\} \)
تهیه کننده : مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
اشتراک و اجتماع و تفاضل در مجموعه ها
فصل 1 : مجموعه ها
اجتماع دو مجموعه
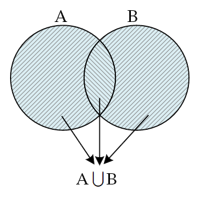
اجتماع دو مجموعه A و B شامل همه عضو هایی است که حداقل در یکی از دو مجموعه A و B باشند و اجتماع دو مجموعه A و B را بصورت \(A \cup B\) نشان می دهند.
نمودار ون اجتماع دو مجموعه A و B
اشتراک دو مجموعه
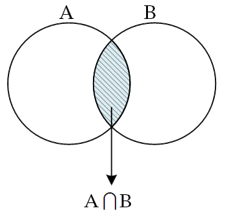
اشتراک دو مجموعه A و B شامل همه عضوهایی که هم عضو A و هم عضو B باشند و اشتراک دو مجموعه A و B را به صورت \(A \cap B\) نمایش می دهند.
نمودار ون اشتراک دو مجموعه A و B
تفاضل دو مجموعه
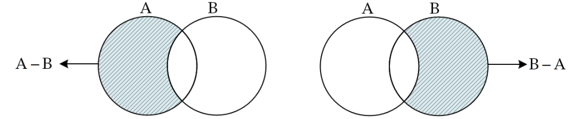
مجموعه A – B (A منهای B) شامل همه عضوهایی است که عضو مجموعه A باشند ولی عضو مجموعه B نباشند.
نمودار ون تفاضل دو مجموعه A و B
مثال
اگر مجموعه \(A = \{ 1\,,\,2\,,\,3\} \) و \(B = \{ x|x \in \mathbb{Z}\,,\, - 2 < x \le 2\} \) و \(C = \{ {x^2} + 1|x \in A\} \) باشد، عضوهای هر مجموعه را همراه با مجموعه های خواسته شده در زیر بنویسید.
\(\begin{array}{l}B = \{ x|x \in \mathbb{Z}\,,\, - 2 < x \le 2\} = \{ - 1\,,\,0\,,\,1\,,\,2\} \\\\C = \{ {x^2} + 1|x \in A\} = \{ 2\,,\,5\,,\,10\} \end{array}\)
الف \(A - C\)
\(A - C = \{ 1\,,\,2\,,\,3\} - \{ 2\,,\,5\,,\,10\} = \{ 1\,,\,3\} \)
ب \(B \cap (A \cup C)\)
\(\begin{array}{l}B \cap (A \cup C) = \{ - 1\,,\,0\,,\,1\,,\,2\} \cap (\{ 1\,,\,2\,,\,3\} \cup \{ 2\,,\,5\,,\,10\} ) = \\\\\{ - 1\,,\,0\,,\,1\,,\,2\} \cap \{ 1\,,\,2\,,\,3\,,\,5\,,\,10\} = \{ 1\,,\,2\} \end{array}\)
مثال
با توجه به هر شکل مجموعه های داده شده را هاشور بزنید؟
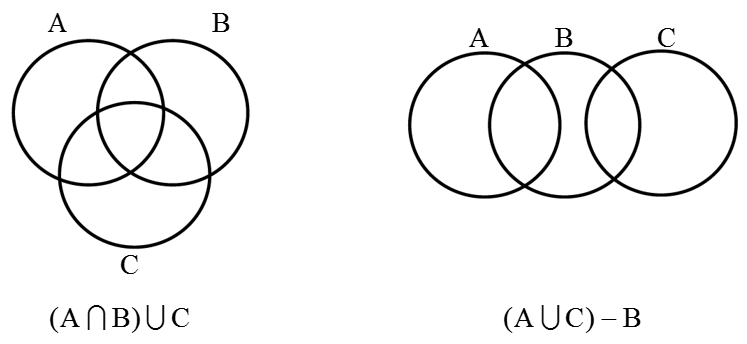
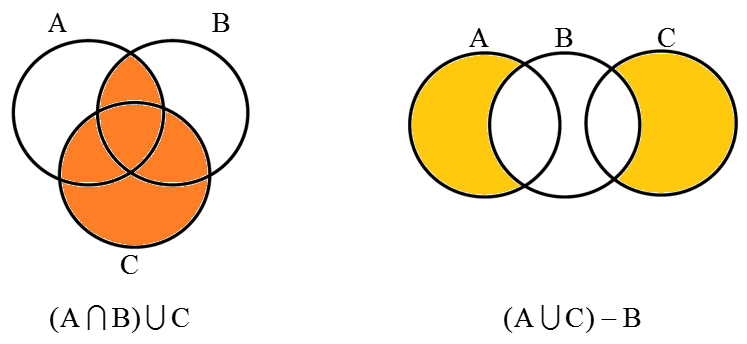
تهیه کننده : مسعود زیرکاری
مجموعه و احتمال
فصل 1 : مجموعه ها
مجموعه و احتمال
برای به دست آوردن احتمال هر پیشامد از رابطه ی زیر استفاده می کنیم:
مثال
در پرتاب یک تاس احتمال های زیر را به دست آورید.
الف احتمال آمدن عدد اول
\(\begin{array}{l}S = \{ 1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\} \Rightarrow n(S) = 6\\\\A = \{ 2\,,\,3\,,\,5\} \Rightarrow n(A) = 3 \Rightarrow p(A) = \frac{{n(A)}}{{n(S)}}\\\\ \Rightarrow p(A) = \frac{3}{6} = \frac{1}{2}\end{array}\)
ب احتمال آمدن عدد بزرگتر و مساوی 5
\(B = \{ 5\,,\,6\} \Rightarrow n(B) = 2 \Rightarrow p(B) = \frac{{n(B)}}{{n(S)}} \Rightarrow p(B) = \frac{2}{6} = \frac{1}{3}\)
در پرتاب دو تاس احتمال های زیر را به دست آورید.
الف) احتمال آمدن این که تاس اول عدد فرد و تاس دوم عدد کوچکتر از 3 بیاید.
کل حالت ها\(n(S) = {6^2} = 36\)
\(\begin{array}{l}A = \{ (1\,,\,1)\,,\,(1\,,\,2)\,,\,(3\,,\,1)\,,\,(3\,,\,2)\,,\,(5\,,\,1)\,,\,(5\,,\,2)\} \Rightarrow n(A) = 6\\\\ \Rightarrow p(A) = \frac{6}{{36}} = \frac{1}{6}\end{array}\)
ب) احتمال آمدن این که مجموع هر دو عدد تاس 6 شود.
\(\begin{array}{l}B = \{ (1\,,\,5)\,,\,(5\,,\,1)\,,\,(2\,,\,4)\,,\,(4\,,\,2)\,,\,(3\,,\,3)\} \Rightarrow n(B) = 5\\\\ \Rightarrow p(B) = \frac{5}{{36}}\end{array}\)
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ضرب و تقسیم و جمع و تفریق اعداد گویا
فصل 2 : عددهای حقیقی
اعداد گویا
هر عددی که به کسر تبدیل شود عدد گویا نام دارد.( صورت و مخرج عدد صحیح و مخرج مخالف صفر باشد)
اعداد گویا را با حرف انگلیسیQ نمایش می دهند:
\(Q = \{ \left. {\frac{a}{b}} \right|{\rm{ }}a,b \in z,b \ne 0\} \)
جمع و تفریق اعداد کسری
مخرج مشترک گرفته که بهترین مخرج مشترک همان )ب . م. م) مخرج ها است.
مانند :
\(\left( { - \frac{5}{{12}}} \right) - \left( { - \frac{7}{{18}}} \right) = \frac{{ - 15 + 14}}{{36}} = - \frac{1}{{36}}\)(ب. م . م) مخرج ها \( \Rightarrow \left( {12,18} \right) = 36\)
ضرب اعداد کسری
فقط در ضرب میتوان قبل از جواب دادن صورت را با مخرج ساده کرد. سپس صورت ها در هم و مخرج ها در هم ضرب می شود.
مانند :
تقسیم اعداد کسری
تقسیم به ضرب تبدیل میشود کسر اولی در معکوس کسر دومی ضرب می شود.
(کسر اولی در معکوس کسر دومی ضرب می شود)
مانند :
مثال
حاصل عبارت زیر را به دست آورید.
\(\left( { + \frac{2}{3}} \right) \div \left[ {\left( { - \frac{1}{5}} \right) + \left( { + \frac{3}{5}} \right)} \right]\)
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
مقایسه کسرها
فصل 2 : عددهای حقیقی
مقایسه کسرها
از دو روش می توان استفاده کرد :
الف) هم مخرج کردن کسرها : ابتدا مخرج تمام کسرها را برابر کرده سپس کسرها را مقایسه می کنیم.
مثال
کسرهای زیر را از کوچک به بزرگ مرتب کنید.
\(\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}}\)
\(\begin{array}{l}\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}} \Rightarrow \frac{8}{{20}},\frac{{15}}{{20}},\frac{{10}}{{20}},\frac{{14}}{{20}} \Rightarrow \frac{2}{5} < \frac{1}{2} < \frac{7}{{10}} < \frac{3}{4}\\\\\left( {2,45,10} \right) = 20\end{array}\)
ب) تبدیل به عدد اعشار : صورت بر مخرج تقسیم و خارج قسمت تا دو رقم اعشار ادامه می دهیم.
مثال
کسرهای زیر را از کوچک به بزرگ مرتب کنید.
\(\frac{2}{5},\frac{3}{4},\frac{1}{2},\frac{7}{{10}}\)
\(\begin{array}{l}\frac{2}{5} = 0/40{\rm{ }},{\rm{ }}\frac{3}{4} = 0/75{\rm{ , }}\frac{1}{2} = 0/50{\rm{ , }}\frac{7}{{10}} = 0/70\\\\\frac{2}{5},\frac{1}{2},\frac{7}{{10}},\frac{3}{4}\end{array}\)
بین هر دو عدد گویا بی نهایت عدد گویا وجود دارد.
پیدا کردن کسرهایی بین دو عدد کسری
چند روش وجود دارد که دو روش کاربردی آن به صورت زیر است :
۱) صورت ها با هم و مخرج ها با هم جمع می کنیم
۲) ابتدا مخرج مشترک گرفته سپس صورت و مخرج را در یک واحد بیشتر از تعداد خواسته شده ضرب کنیم.
مثال
بین \(\frac{4}{5},\frac{3}{4}\) دو عدد گویا بنویسید؟
روش اول:
\(\frac{3}{4} < \frac{7}{9} < \frac{{11}}{{14}} < \frac{4}{5}\)
روش دوم:
\(\frac{3}{4},\frac{4}{5} \Rightarrow \frac{{15}}{{20}},\frac{{16}}{{20}} \Rightarrow \frac{{45}}{{60}},\frac{{48}}{{60}} \Rightarrow \frac{{45}}{{60}} < \frac{{46}}{{60}} < \frac{{47}}{{60}} < \frac{{48}}{{60}}\)
تهیه کننده:مسعود زیرکاری
تبدیل کسر به اعداد اعشاری
فصل 2 : عددهای حقیقی
عددهای اعشاری متناهی یا مختوم
اگر باقیمانده صورت بر مخرج کسر صفر شود آن کسر را مختوم نام دارد.مانند :
\(\frac{3}{4} = 0/75{\rm{ }},{\rm{ }}\frac{6}{5} = 1/25\)
اگر در تجزیه مخرج کسر عامل ۲ و ۵ باشند آن کسر مختوم است. مانند :
\(\begin{array}{l}\frac{3}{{20}} \Rightarrow 20 = {2^2} \times 5\\\\\frac{5}{8} \Rightarrow 8 = {2^3}\end{array}\)
عددهای اعشاری متناوب ساده
اگر در تقسیم صورت بر مخرج کسر در خارج قسمت عددی مرتب تکرار شود آن را متناوب ساده می گویند. مانند : (خط تیره روی عدد به معنی تکرار یا گردش عدد است.)
\(\begin{array}{l}\frac{5}{{11}} = 0/4545000 = 0/\overline {45} \\\\\frac{1}{3} = 0/33000 = 0/\overline 3 \end{array}\)
اگر در تجزیه مخرج کسر عامل ۲ و ۵ نباشند آن کسر متناوب ساده است، مانند :
\(\frac{3}{{77}} \Rightarrow 77 = 7 \times 11{\rm{ , }}\frac{6}{{13}}\)
عددهای اعشاری متناوب مرکب
اگر در تقسیم صورت بر مخرج کسر در خارج قسمت بعد از یک یا چند رقم اعشار به رقم های تکراری برسند به آن کسر متناوب مرکب می گویند؛ مانند :
\(\begin{array}{l}\frac{5}{6} = 0/833000 = 0/8\overline 3 {\rm{ }}\\,\\\frac{7}{{22}} = 0/31818000 = 0/3\overline {18} \end{array}\)
اگر در تجزیه مخرج کسر غیر از عامل ۲ و ۵ عامل دیگری باشند آن کسر متناوب مرکب است.
مانند:
\(\begin{array}{l}\frac{5}{{14}} \Rightarrow 14 = 2 \times 7\\,\\\frac{2}{{75}} \Rightarrow 75 = 3 \times {5^2}\end{array}\)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اعداد گنگ
فصل 2 : عددهای حقیقی
اعداد گنگ یا اصم
اعداد که تعداد ارقام اعشاری آنها نامتناهی و دارای دوره تناوب نباشند اعداد گنگ نام دارند.
1 مجموعه اعداد گنگ را با حرف انگلیسی Q یا \({Q^C}\) نشان می دهند.
2 اگر n مربع کامل نباشد آنگاه \(\sqrt n \) عددی گنگ است )یعنی اعدادی که جذر دقیق ندارند عدد گنگ هستند)
3 عدد \(\pi \)چون دارای دوره تناوب نیست عدد گنگ است )عدد\(\pi \)تا ۱۰ رقم اعشار :\(\pi = 3/1415926535\) )
4 بین دو عدد بی نهایت عدد گنگ وجود دارد.
مثال
بین هر دو عدد داده شده دو عدد گنگ بنویسید.
الف \(\sqrt 3 ,\sqrt 4 \)
\(\sqrt 3 < \sqrt {3/1} < \sqrt {3/2} < \sqrt 4 \)
ب\(3,2\)
\(2 = \sqrt 4 < \sqrt 5 < \sqrt 6 < \sqrt 9 = 3\)
مثال
عدد \(3 - \sqrt {10} \) بین کدام دو عدد صحیح متوالی قرار دارد؟
\(3 - \sqrt {16} < 3 - \sqrt {10} < 3 - \sqrt 9 \Rightarrow - 1 < 3 - 10 < 0\)
بین 0 و1 قرار دارد.
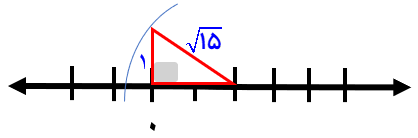
اعداد\(1 - \sqrt 5 ,\sqrt {17} \) را روی محور اعداد نمایش دهید.:
الف\(1 - \sqrt 5 \)
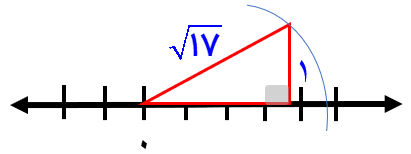
ب\(\sqrt {17} \)
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
اعداد حقیقی
فصل 2 : عددهای حقیقی
اعداد حقیقی
اجتماع مجموعه اعداد گویا و اعداد گنگ مجموعه اعداد حقیقی را تشکیل می دهد
\(Q \cup Q' = R\)
1 مجموعه اعداد حقیقی را با حرف انگلیسی R نشان می دهند.
2 نمودار ون مجموعه اعداد طبیعی (N) و اعداد حسابی (W) و اعداد صحیح (Z) و اعداد گویا (Q) و اعداد گنگ (Q’) و اعداد حقیقی (R) به صورت زیر است :
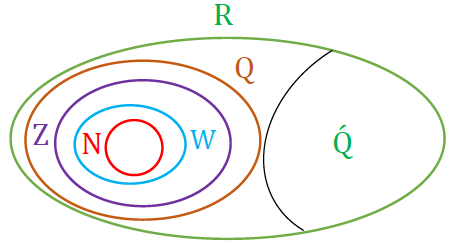
\(N \subseteq W \subseteq Z \subseteq Q \subseteq R{\rm{ }},{\rm{ }}Q' \subseteq R\)
نمایش اعداد حقیقی روی محور
چون اعداد حقیقی شامل اعداد گویا و گنگ هستند پس نمایش این اعداد به صورت یک خط ممتدی است. ( اگر علامت نامساوی سرکش داشته باشد دایره توپر و بدون سرکش دایره تو خالی قرار می دهیم)
مثال
مجموعه اعداد زیر را روی محور نشان دهید.
الف \(A = \{ x \in \left. R \right| - 2 \le x < 3\} \)
ب \(B = \{ x \in \left. R \right|1 \le x\} \)
مثال
مجموعه متناظر محور مقابل را بنویسید.
\(C = \{ x \in \left. R \right| - 3 < x < 3\} \)
تهیه کننده:مسعود زیرکاری
قدر مطلق
فصل 2 : عددهای حقیقی
قدر مطلق
فاصله ی نقطه نمایش یک عدد مانند a را از مبدا مختصات قدر مطلق a می نامیم و آن را به صورت |a| نشان می دهیم.
خواص قدر مطلق
الف) قدر مطلق عدد مثبت برابر است با خود آن عدد :\(x\rangle 0 \Rightarrow \left| x \right| = x\)
ب( قدر مطلق صفر برابر با صفر است :\(x = 0 \Rightarrow \left| x \right| = 0\)
ج) قدر مطلق عدد منفی برابر با قرینه آن عدد است :\(x < 0 \Rightarrow \left| x \right| = - x\)
مثال
عبارت های زیر را بدون استفاده از نماد قدر مطلق بنویسید.
1 \(\left| {4 - 6 \times {2^2} \div 3 + 2} \right|\)
\(\left| {4 - 6 \times {2^2} \div 3 + 2} \right| = \left| { - 2} \right| = 2\)
2 \(\left| {3 - \sqrt 2 } \right|\)
\(\left| {3 - \sqrt 2 } \right| = 3 - \sqrt 2 \)
3 \(\left| {{a^{20}} - {a^{30}}} \right|\)
\(\left| {{a^{20}} - {a^{30}}} \right| = {a^{30}} - {a^{20}}\)
مثال
اگر \(x = \frac{2}{3}\,\,,\,\,z = - \frac{1}{2}\,\,,\,\,y = 3\)باشد. حاصل عبارت زیر را به دست آورید.
\(\left| { - 6x - 4z} \right| + 2\left| y \right|\)
\(\left| { - 6x - 4z} \right| + 2\left| y \right| = \left| { - 6\left( {\frac{2}{3}} \right) - 4\left( { - \frac{1}{2}} \right)} \right| + 2\left| 3 \right| = \left| { - 4 + 2} \right| + 2\left( 3 \right) = 2 + 6 = 8\)
با توجه به مفهوم قدر مطلق همواره رابطه مقابل برقرار است :\(\sqrt {{a^2}} = \left| a \right|\)
حاصل هر عبارت را به دست آورید.
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} = \left| {2 - \sqrt 5 } \right| = - \left( {2 - \sqrt 5 } \right) = \sqrt 5 - 2\)
\(\sqrt {{{\left( {3\sqrt 2 - 2\sqrt 2 } \right)}^2}} \)
\(\sqrt {{{\left( {3\sqrt 2 - 2\sqrt 2 } \right)}^2}} = \left| {3\sqrt 2 - 2\sqrt 2 } \right| = 3\sqrt 2 - 2\sqrt 2 \)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
استدلال و اثبات در هندسه
فصل 3 : استدلال و اثبات در هندسه
استدلال
دلیل آوردن و استفاده از معلومات قبلی برای معلوم شدن موضوعی که در ابتدا مشخص نبوده است.
اثبات
به استدلالی که موضوع مورد نظر را به درستی نتیجه دهد اثبات می گوییم.
مثال نقض
برای رد یک ادعای ریاضی از مثال نقض استفاده می کنیم
همواره برای اثبات یک مسئله نمیتوان از رسم شکل یا شهود استفاده کرد زیرا ممکن است خطای دید در آن شکل وجود داشته باشد.
مثال
برای هر یک از مسئله های زیر یک مثال نقض بزنید :
الف تمام اشکال هندسی گوشه یا زاویه دارند؟
دایره یک شکل هندسی است که دارای گوشه و زاویه نیست.
ب تمام اعداد زوج اول هستند؟
عدد ۲ تنها عدد زوجی است که اول نیز است.
مثال
کدام یک از استدلال های زیر منطقی و کدام غیر منطقی است :
الف علی می گوید : هر وقت من درس نخواندم همان روز معلم از من سوال می کند؟
غیر منطقی
ب تصادف منجر به مرگ در جادها ممکن است به دلیل نقض فنی ماشین باشد؟
منطقی
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
فرض و حکم مسئله
فصل 3 : استدلال و اثبات در هندسه
فرض مسئله
اطلاعاتی که در مسئله داده شده یا حقایقی که مربوط به آن مسئله باشد. (به طور خلاصه داده ها مسئله)
حکم مسئله
خواسته های مسئله را حکم مسئله میگویند.
مثال
در هر مسئله فرض و حکم را مشخص کنید :
الف زاویه های روبه رو لوزی برابرند
فرض : خواص لوزی
حکم : برابر بودن زاویه های رو به رو
ب طول دو مماس در دایره همواره برابرند
فرض: دایره و عمود بودن خط مماس بر شعاع
حکم : برابر بودن دو مماس
مثال
با توجه به مفروضات داده شده نتیجه حاصل را بنویسید :
الف در مربع قطرها عمود منصف یکدیگرند و همچنین لوزی نوعی مربع است
در لوزی قطرها عمود منصف یکدیگرند
ب هر چهار ضلعی که زاویه قائمه داشته باشد مستطیل است و همچنین مربع دارای زاویه قائمه است
مربع نوعی مستطیل است
ثابت کنید زاویه های متقابل به راس با هم برابرند.
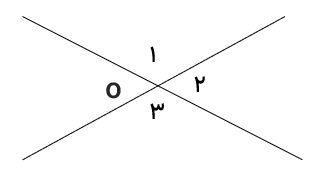
فرض : \(\widehat {{o_1}} = \widehat {{o_3}}\) دو زاویه متقابل به راس
حکم : \(\widehat {{o_1}} = \widehat {{o_3}}\)
\(\left. \begin{array}{l}\widehat {{o_1}} + \widehat {{o_2}} = 180^\circ \\\\\widehat {{o_2}} + \widehat {{o_3}} = 180^\circ \end{array} \right\} \Rightarrow \widehat {{o_1}} + \widehat {{o_2}} = \widehat {{o_2}} + \widehat {{o_3}} \Rightarrow \widehat {{o_1}} = \widehat {{o_3}}\)
ثابت کنید زاویه ی خارجی مثلث برابر است با مجموع دو زاویه ی داخلی غیر مجاور آن.
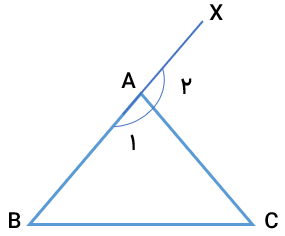
فرض : \({A_2}\) زاویه ی خارجی مثلث
حکم :\(\widehat {{A_2}} = \widehat B + \widehat C\)
\(\left. \begin{array}{l}\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \\\\\widehat {{A_1}} + \widehat B + \widehat C = 180^\circ \end{array} \right\} \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = \widehat {{A_1}} + \widehat B + \widehat C \Rightarrow \widehat {{A_2}} = \widehat B + \widehat C\)
تهیه کننده: مسعود زیرکاری
هم نهشتی مثلث ها
فصل 3 : استدلال و اثبات در هندسه
هم نهشتی مثلث ها
دو مثلث به سه حالت هم نهشت هستند :
الف) دو ضلع مساوی و زاویه بین مساوی )ض ز ض)
ب) دو زاویه مساوی و ضلع بین مساوی (ز ض ز (
ج) سه ضلع مساوی (ض ض ض)
سه زاویه مساوی )ز ز ز( از حالتهای هم نهشتی نیست.
هم نهشتی دو مثلث قائم الزاویه
دو مثلث قائم الزاویه به دو حالت هم نهشت هستند :
الف) وتر و یک زاویه ی تند (و ز)
ب) وتر و یک ضلع (و ض)
نکاتی درباره هم نهشتی دو مثلث
الف) اگر دو مثلث به هم چسبیده باشند دارای ضلع مشترک هستند.
ب) اگر دو مثلث به صورت ضربدری باشند دارای زاویه متقابل به راس هستند.
ج) اگر دو مثلث داخل دایره باشند از برابری شعاع دایره استفاده می کنیم.
د) در مثلث متساوی الاضلاع هر سه ضلع و هر سه زاویه برابرند.
ه) در مثلث متساوی الساقین دو ساق و دو زاویه ی مجاور قاعده برابرند.
در دو مثلث هم نهشت اضلاع و زاویه های متناظر برابرند.
مثال
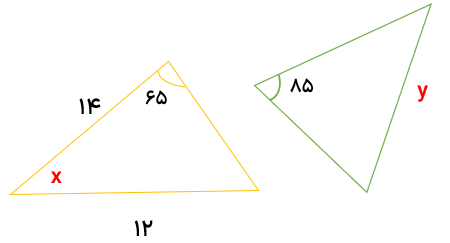
دو مثلث زیر هم نهشت هستند مقادیر مجهول را مشخص کنید.
(در دو مثلث هم نهشت اضلاع و زاویه های متناظر برابرند)
(مجوع زاویه های داخلی مثلث ۱۸۰ درجه است)
۳۰ = (۶۵ + ۸۵) - ۱۸۰
y = ۱۴ , X=30
مثال
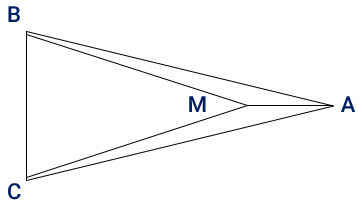
در شکل زیر دو مثلث ABC و MBC متساوی الساقین هستند دلیل هم نهشتی دو مثلث AMC و AMB را بنویسید.
فرض : AB = AC,MB = MC
حکم : \(A\mathop M\limits^\Delta B \cong A\mathop M\limits^\Delta C\)
\(\left. \begin{array}{l}AB = AC\\MB = MC\\AM = AM\end{array} \right\} \Rightarrow A\mathop M\limits^\Delta B \cong A\mathop M\limits^\Delta C\)
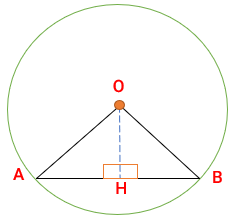
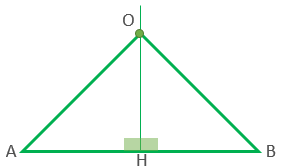
با توجه به شکل زیر نشان دهید خطی که از مرکز دایره بر وتر عمود میشود آن وتر را نصف می کند.
فرض : Oمرکز دایره و OH عمود برAB
حکم : AH = HB
\(\left. \begin{array}{l}OA = OB\\\widehat {{H_1}} = \widehat {{H_2}} = 90^\circ \\OH = OH\end{array} \right\} \Rightarrow A\mathop H\limits^\Delta O \cong B\mathop H\limits^\Delta O \Rightarrow AH = HB\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
قدم های حل مسئله
فصل 3 : استدلال و اثبات در هندسه
قدم های حل مسئله
برای حل مسئله ۴ گام (قدم) نیاز است :
۱) درک و فهم مسئله
۲) رسم شکل
۳) نوشتن فرض و حکم مسئله
4)راهبرد حل مسئله
مثال
نشان دهید هر نقطه روی عمود منصف قرار داشته باشد از دو سر پاره خط به یک اندازه است.
گام اول: درک و فهم مسئله عمود منصف خطی بر خط رسم شده عمود باشد و آن خط را نصف کند.
گام دوم : (رسم شکل)
گام سوم: نوشتن فرض و حکم
فرض : OH عمود منصف
حکم : OA = OB
گام چهارم: (راهبرد حل مسئله)
هم نهشتی به طریق دوضلع و زاویه بین (ض ز ض)
\(\left. \begin{array}{l}AH = HB\\\widehat {{H_1}} = \widehat {{H_2}}\\OH = OH\end{array} \right\} \Rightarrow A\mathop H\limits^\Delta O \cong B\mathop H\limits^\Delta O \Rightarrow OA = OB\)
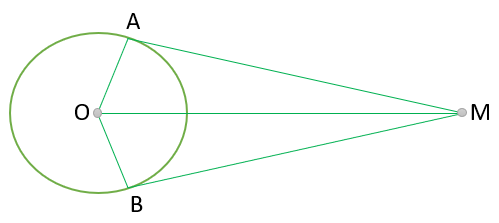
نشان دهید طول دو مماس رسم شده از نقطه خارج دایره با هم برابر هستند.
گام اول: (درک و فهم مسئله) شعاع دایره برخط مماس عمود و در دایره دو شعاع با هم برابرند.
گام دوم: (رسم شکل)
گام سوم : (نوشتن فرض و حکم)
فرض : \(OA = OB,\widehat A = \widehat B = 90^\circ \)
حکم : MA = MB
گام چهارم: راهبرد حل مسئله
هم نهشتی به طریق (و ض)
\(\left. \begin{array}{l}OA = OB\\\widehat A = \widehat B = 90^\circ \\OM = OM\end{array} \right\} \Rightarrow M\mathop A\limits^\Delta O = M\mathop B\limits^\Delta O \Rightarrow MA = MB\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
دو شکل متشابه
فصل 3 : استدلال و اثبات در هندسه
دو شکل متشابه
دو شکلی که اضلاع به یک نسبت تغییر کند )کوچک یا بزرگ یا بدون تغییر( ولی زاویه ها تغییر نکرده باشد دو شکل متشابه می گویند.
1 دو مربع دلخواه و دو مثلث متساوی الاضلاع همواره متشابه هستند.
2 دو مستطیل همواره متشابه نیست چون اضلاع ممکن است به یک اندازه تغییر نکند
3 دو لوزی دلخواه همواره متشابه نیست چون ممکن است زاویه ها دو به دو برابر نباشند
4 نسبت اضلاع متناظر دو شکل متشابه را نسبت تشابه می گویند.
5 دو شکل هم نهشت همواره متشابه و نسبت تشابه آنها عدد یک است.
مثال
دو مثلث ABC و DEF متشابه هستند اگر اضلاع مثلث ABC به اندازه های ۳ و ۴ و ۶ و اضلاع مثلث DEF به اندازه های \(x - 3,8,2y\) باشند : (اضلاع دو مثلث از کوچک به بزرگ نوشته شده اند)
الف مقدار x و y را به دست آورید.
\(\frac{3}{{2y}} = \frac{4}{8} = \frac{6}{{x - 3}} \Rightarrow \left\{ \begin{array}{l}\frac{3}{{2y}} = \frac{4}{8} \Rightarrow 8y = 24 \Rightarrow y = 3\\\\\frac{4}{8} = \frac{6}{{x - 3}} \Rightarrow 4x - 12 = 48 \Rightarrow 4x = 60 \Rightarrow x = 15\end{array} \right.\)
ب نسبت تشابه دو مثلث را بنویسید.
\(\frac{4}{8} = \frac{1}{2}\)
مثال
مقیاس نقشه ای ۱۰۰۰۰۰ : ۱ است. اگر طول جاده ای روی این نقشه ۱۲ سانتی متر باشد :
الف طول واقعی جاده چند کیلومتر است؟
\(\begin{array}{l}\frac{1}{{100000}} = \frac{{12}}{x} \Rightarrow x = 1200000cm\\\\1200000 \div 100000 = 12km\end{array}\)
تبدیل واحد : هر کیلو متر ۱۰۰۰۰۰ سانتی متر است
ب اگر اندازه ی یکی از زاویه های روی نقشه ۴۰ درجه باشد اندازه این زاویه در واقعیت چند درجه است؟
در دو شکل متشابه زاویه تغییر نمیکند پس زاویه در واقعیت نیز ۴۰ درجه است.
در دو مثلث متشابه :
الف نسبت محیط و ارتفاع و نیمساز و عمود منصف و میانه با نسبت تشابه برابر است.
ب نسبت مساحت با مجذور نسبت تشابه برابر است.
نسبت تشابه دو مثلث \(\frac{3}{5}\) می باشد :
الف نسبت میانه دو مثلث چند است؟
\(\frac{3}{5}\)
ب نسبت مساحت دو مثلث چند است؟
\({\left( {\frac{3}{5}} \right)^2} = \frac{9}{{25}}\)
تهیه کننده: مسعود زیرکاری
اعداد توان دار
فصل 4 : توان و ریشه
توان
اگر عددی چند بار در خودش ضرب شود برای خلاصه نویسی از توان استفاده می شود.
مثال
ضرب اعداد توان دار
الف) اگر پایه ها برابر باشند: یکی از پایه ها را نوشته و توان ها را با هم جمع می کنیم.
مثال
\(\begin{array}{l}{a^m} \times {a^n} = {a^{m + n}}\\\\{4^7} \times {4^3} = {4^{10}}\end{array}\)
ب) اگر توان ها برابر باشند: یکی از توان ها را نوشته و پایه ها را در هم ضرب می کنیم.
مثال
\(\begin{array}{l}{a^m} \times {b^m} = {(ab)^m}\\\\{12^7} \times {3^7} = {36^7}\end{array}\)
تقسیم اعداد توان دار
الف) اگر پایه ها برابر باشند: یکی از پایه ها را نوشته و توان ها را از هم کم میکنیم
مثال
\(\begin{array}{l}{a^m} \div {a^n} = {a^{m - n}}\\\\\frac{{{9^5}}}{{{9^3}}} = {9^2}\end{array}\)
ب) اگر توان ها برابر باشند: یکی از توان ها را نوشته و پایه ها را بر هم تقسیم می کنیم.
مثال
\(\begin{array}{l}{a^m} \div {b^m} = {(\frac{a}{b})^m}\\\\{20^8} \div {4^8} = {5^8}\end{array}\)
1 اگر در ضرب و تقسیم اعداد توان دار پایه ها و توانها برابر نباشند از تجزیه استفاده می کنیم.
مانند :
\(\begin{array}{l}{4^8} \times {2^3} = {({2^2})^8} \times {2^3} = {2^{19}}\\\\{9^2} \div 27 = {({3^2})^2} \div {3^2} = 3\end{array}\)
2 اگر اعداد توان دار مثل هم باشند و بین آنها علامت جمع باشد آن عبارت را تبدیل به ضرب می کنیم.
\(\begin{array}{l}{2^6} + {2^6} = 2 \times {2^6} = {2^7}\\\\{9^5} \times {9^5} \times {9^5} = 3 \times {9^5} = {3^1} \times {({3^2})^5} = {3^{11}}\end{array}\)
تهیه کننده :مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
توان منفی
فصل 4 : توان و ریشه
توان منفی
برای به دست آوردن توان منفی عدد پایه را معکوس کرده تا به توان مثبت تبدیل شود.
\({a^{ - n}} = {(\frac{1}{a})^n}\)
1 تمام قواعد اعداد توان دار برای اعداد با توان منفی صدق می کند.
2 اگر عدد صحیحی غیر از صفر از صورت به مخرج و یا از مخرج به صورت انتقال داده شود توان آن قرینه می شود.
مثال
حاصل هر عبارت را به صورت توان طبیعی (توان مثبت) بنویسید.
\({5^{ - 6}}\)
\({5^{ - 6}} = {(\frac{1}{5})^6}\)
\({3^{ - 4}} \times {3^2} \div 27\)
\({3^{ - 4}} \times {3^2} \div 27 = {3^{ - 4}} \times {3^2} \div {3^3} = {3^{ - 5}} = {(\frac{1}{3})^5}\)
\(\frac{{{{20}^{ - 6}}}}{{{5^2} \times {4^{ - 6}}}}\)
\(\frac{{{{20}^{ - 6}}}}{{{5^2} \times {4^{ - 6}}}} = \frac{{{5^{ - 6}}}}{{{5^2}}} = {5^{ - 8}} = {(\frac{1}{5})^8}\)
\(\frac{{{4^7} \times {3^{ - 6}}}}{{{3^3} \times {4^{ - 2}}}}\)
\(\frac{{{4^7} \times {3^{ - 6}}}}{{{3^3} \times {4^{ - 2}}}} = \frac{{{4^7} \times {4^2}}}{{{3^3} \times {3^6}}} = {(\frac{4}{3})^9}\)
هر عدد (غیر از صفر) به توان صفر باشد حاصل عدد یک است.
مثال
حاصل عبارت مقابل را به دست آورید؟
\({3^2} + {5^0} - {2^{ - 2}}\)
\({3^2} + {5^0} - {2^{ - 2}} = 9 + 1 - \frac{1}{4} = \frac{{40 - 1}}{4} = \frac{{39}}{4} = 9\frac{3}{4}\)
تهیه کننده :مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
نماد علمی
فصل 4 : توان و ریشه
نماد علمی
برای محاسبه ساده تر اعداد خیلی بزرگ و اعداد خیلی کوچک آنها را به صورت توانی از عدد ۱۰ می نویسیم.
به طور کلی نماد علمی هر عدد اعشاری مثبت به صورت \(a \times {10^n}\) است که در آن \(1 \le a < 10\) وn عدد صحیحی است.
الف نماد علمی اعداد خیلی بزرگ توان (مثبت) ابتدا یک رقم از سمت چپ جدا کرده سپس به تعداد رقم های بعد از ممیز توانی از عدد ۱۰ می نویسیم
مانند :
\(\begin{array}{l}341000000 = 3/41 \times {10^8}\\\\14752/93 = 1/475293 \times {10^4}\end{array}\)
ب نماد علمی اعداد خیلی کوچک توان منفی ابتدا یک رقم مخالف صفر از سمت چپ جدا کرده سپس به تعداد رقم های قبل از ممیز توانی از عدد ۱۰ می نویسیم.
مانند :
\(\begin{array}{l}0/0000037 = 3/7 \times {10^{ - 6}}\\\\0/00678 = 6/78 \times {10^{ - 3}}\end{array}\)
مثال
حاصل عبارت زیر را به صورت نماد علمی بنویسید.
\(530000 \times 0/00027\)
\(530000 \times 0/00027 = 5/3 \times {10^5} \times 2/7 \times {10^{ - 4}} = 14/32 \times {10^1} = 1/432 \times {10^2}\)
تهیه کننده :مسعود زیرکاری
ریشه گیری
فصل 4 : توان و ریشه
ریشه گیری
الف) ریشه دوم اعداد هر عدد دارای دو ریشه دوم است :(یکی مثبت و دیگری منفی)
مانند :
\({4^2} = {( - 4)^2} = 16 \Rightarrow \sqrt {16} = 4, - 4\)
ریشه های دوم ۱۶ برابر است با ۴ و ۴-
ب) ریشه سوم اعداد هر عدد دارای یک ریشه سوم است.
اعداد منفی جذر )ریشه دوم( ندارند (چون مجذور دو عدد مثل هم هیچ وقت منفی نمی شود)
اگر a یک عدد حقیقی باشد ریشه سوم آن را به صورت \(\sqrt[3]{a}\) نشان می دهیم.
مانند :
\(\begin{array}{l}{3^3} = 27 \Rightarrow \sqrt[3]{{27}} = 3\\\\{( - 3)^3} = - 27 \Rightarrow \sqrt[3]{{ - 27}} = - 3\end{array}\)
مثال
حاصل جذرهای زیر را به دست آورید.
\(\sqrt {64 \times \frac{1}{9}} \)
\(\sqrt {64 \times \frac{1}{9}} = 8 \times \frac{1}{3} = \frac{8}{3}\)
\(4\sqrt[3]{{ - 125}}\)
\(4\sqrt[3]{{ - 125}} = 4 \times - 5 = - 20\)
\(\sqrt {64} \times \sqrt[3]{{ - 64}}\)
\(\sqrt {64} \times \sqrt[3]{{ - 64}} = 8 \times - 4 = - 32\)
\(\sqrt[3]{{0/001}} \times \sqrt {\sqrt {16} } \)
\(\sqrt[3]{{0/001}} \times \sqrt {\sqrt {16} } = 0/1 \times 2 = 0/2\)
تهیه کننده :مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ضرب و تقسیم و ساده کردن رادیکال ها
فصل 4 : توان و ریشه
ضرب و تقسیم رادیکال ها
اگر دو رادیکال دارای ریشه (فرجه یکسان باشند میتوانیم آنها را در هم ضرب یا بر هم تقسیم کنیم.
اگر رادیکال ها دارای عدد صحیح باشند ابتدا اعداد صحیح را ضرب یا تقسیم کرده سپس رادیکال ها را ضرب یا تقسیم می کنیم.
مثال
حاصل ضرب و تقسیم های زیر را به دست آورید.
\(2\sqrt 2 \times \sqrt 8 \)
\(2\sqrt 2 \times \sqrt 8 = 2\sqrt {16} = 2 \times 4 = 8\)
\(\sqrt[3]{{ - 2}} \times \sqrt[3]{{32}}\)
\(\sqrt[3]{{ - 2}} \times \sqrt[3]{{32}} = \sqrt[3]{{ - 64}} = - 4\)
\(8\sqrt {50} \div 4\sqrt 2 \)
\(8\sqrt {50} \div 4\sqrt 2 = 2\sqrt {25} = 2 \times 5 = 10\)
\(9\sqrt[3]{{54}} \div 3\sqrt[3]{2}\)
\(9\sqrt[3]{{54}} \div 3\sqrt[3]{2} = 3\sqrt[3]{{27}} = 3 \times 3 = 9\)
ساده کردن رادیکال ها
بعضی از رادیکال ها را میتوان ساده کرد. به این صورت که برای عدد یک ضربی بنویسیم که یکی از آن اعداد ریشه دوم یا ریشه سوم داشته باشد.
مثال
\(\begin{array}{l}\sqrt {20} = \sqrt {4 \times 5} = 2\sqrt 5 \\\\\sqrt[3]{{128}} = \sqrt[3]{{2 \times 64}} = 4\sqrt[3]{2}\\\\\sqrt[3]{{81}} = \sqrt[3]{{3 \times 27}} = 3\sqrt[3]{3}\end{array}\)
تهیه کننده :مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
جمع و تفریق رادیکال ها
فصل 4 : توان و ریشه
جمع و تفریق رادیکال ها
اگر قسمت رادیکال ها پس از ساده کردن مثل هم باشند میتوانیم آنها را همانند عبارت های جبری با هم جمع یا تفریق کنیم.
مانند :
\(5\sqrt 2 - 6\sqrt 5 + 3\sqrt 2 - 6\sqrt 2 - 3\sqrt 5 = 2\sqrt 2 - 9\sqrt 5 \)
مثال
عبارت های زیر را ساده کنید.
\(2\sqrt 2 - \sqrt {75} - 3\sqrt {72} + 4\sqrt 3 \)
\(2\sqrt 2 - \sqrt {75} - 3\sqrt {72} + 4\sqrt 3 = 2\sqrt 2 - \sqrt {3 \times 25} - 3\sqrt {2 \times 36} + 4\sqrt 3 = - 16\sqrt 2 - \sqrt 3 \)
\(\sqrt {18} + 3\sqrt[3]{{ - 54}} + \sqrt[3]{{16}} - 2\sqrt 8 \)
\(\sqrt {18} + 3\sqrt[3]{{ - 54}} + \sqrt[3]{{16}} - 2\sqrt 8 = \sqrt {2 \times 9} + 3\sqrt[3]{{2 \times - 27}} + \sqrt[4]{{2 \times 8}} - 2\sqrt {2 \times 4} = 3\sqrt 2 + - 9\sqrt[3]{2} + 2\sqrt[3]{2} - 4\sqrt 2 = - \sqrt 2 - 7\sqrt[3]{2}\)
گویا کردن مخرج کسرهای رادیکالی
گاهی اوقات برای ساده کردن لازم است مخرج کسر را از حالت رادیکالی بیرون بیاوریم که برای این کار صورت و مخرج را در عددی ضرب میکنیم تا مخرج از حالت رادیکالی خارج شود.
الف) مخرج کسر دارای ریشه دوم باشد: صورت و مخرج را در همان رادیکال مخرج ضرب می کنیم.
مثال
\(\begin{array}{l}\frac{3}{{\sqrt 5 }} = \frac{{3 \times \sqrt 5 }}{{\sqrt 5 \times \sqrt 5 }} = \frac{{3\sqrt 5 }}{5}\\\\\frac{2}{{3\sqrt 2 }} = \frac{{2 \times \sqrt 2 }}{{3\sqrt 2 \times \sqrt 2 }} = \frac{{2\sqrt 2 }}{6} = \frac{{\sqrt 2 }}{3}\end{array}\)
ب) مخرج کسر دارای ریشه سوم باشد صورت و مخرج را در همان رادیکال مخرج ضرب کرده با این تفاوت که عدد زیر رادیکال به توان ۳ برسد. برای این کار فرجه را توان کم کرده تا توان عدد زیر رادیکال مشخص شود.
مثال
\(\begin{array}{l}\sqrt[3]{{\frac{3}{7}}} = \frac{{\sqrt[3]{3}}}{{\sqrt[3]{7}}} = \frac{{\sqrt[3]{3} \times \sqrt[3]{{{7^2}}}}}{{\sqrt[3]{7} \times \sqrt[3]{{{7^2}}}}} = \frac{{\sqrt[3]{{147}}}}{7}\\\\\frac{1}{{\sqrt[3]{{{a^2}}}}} = \frac{{1 \times \sqrt[3]{a}}}{{\sqrt[3]{{{a^2}}} \times \sqrt[3]{a}}} = \frac{{\sqrt[3]{a}}}{a}\end{array}\)
تهیه کننده :مسعود زیرکاری
عبارت های جبری
فصل 5 : عبارت های جبری
عبارت جبری
عبارتی است که از اعداد و متغیر حروف (انگلیسی) تشکیل شده است.
یک جمله ای
عبارت جبری که از دو قسمت تشکیل شده است متغیر و عدد و بین آنها علامتی نباشد. (ضرب است)
مانند :
\( - 4xy,\frac{a}{3}\)
1فرم کلی یک جمله ای به صورت ax است که a عدد حقیقی و x متغیر و 12 عدد حسابی است.
2 هر عدد حقیقی به تنهایی یک جمله ای است چون متغیر آن صفر است.
3 اگر در عبارتی حروف زیر رادیکال یا حروف در مخرج یا حروف توان منفی داشته باشند آن عبارت یک جمله ای نیست.
مثال
کدام عبارت یک جمله ای است؟
\(\sqrt 3 x{y^2},4a + 2,7\sqrt x ,a{b^{ - 2}},\frac{3}{2}\)
\(4a + 2\)
درجه یک جمله ای
توان متغیر را درجه آن یک جمله ای می گویند.
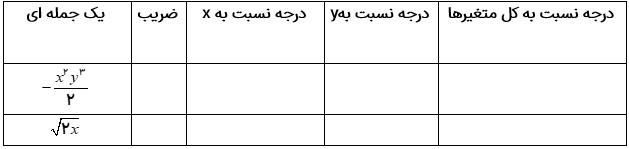
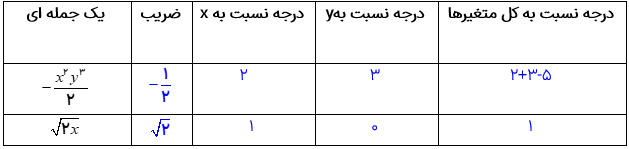
مثال
جدول زیر را کامل کنید.
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
یک جمله ای متشابه
فصل 5 : عبارت های جبری
یک جمله ای متشابه
یک جمله ای که متغیر و توان هر متغیر کاملا مثل هم باشند. مانند\(\left( {4xy, - 3yx} \right)\) که متشابه اند،ولی\(\left( { - 5{a^2}b,3a{b^2}} \right)\) نامتشابه هستند.
جمع و تفریق یک جمله ای های متشابه
ضرایب یک جمله ای را با هم جمع و تفریق می کنیم و متغیرها را کنار آن ها می نویسیم.
مثال
عبارت جبری مقابل را ساده کنید.
\( - 5ab + b - 6 + 3ab + 2b - 8b\)
\( - 5ab + b - 6 + 3ab + 2b - 8b = - 2ab - 5b - 6\)
ضرب و تقسیم یک جمله ای
در ضرب ضرایب در هم و متغیرها در هم ضرب میشود و در تقسیم ضرایب بر هم و متغیرها بر هم تقسیم می شوند.
مثال
عبارت های جبری زیر را ساده کنید.
\(3a( - 4ab - c)\)
\(3a( - 4ab - c) = - 12{a^{2b}} - 3ac\)
\(\frac{{24{x^2}{y^3}z}}{{3xyz}}\)
\(\frac{{24{x^2}{y^3}z}}{{3xyz}} = 8x{y^2}\)
عبارت جبری زیر را ساده کنید.
\( - 6{x^{2 + 5x}}(x - 2y) + 8xy\)
\( - 6{x^{2 + 5x}}(x - 2y) + 8xy = - 6{x^2} + 5{x^2} - 10xy + 8xy = {x^2} - 2xy\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
درجه چند جمله ای
فصل 5 : عبارت های جبری
درجه چند جمله ای
برای تعیین درجه چند جمله ای ، بزرگترین درجه نسبت به آن متغیر را در نظر می گیریم.
مثال
درجه نسبت به متغیر x در چند جمله ای \(\sqrt 5 {x^2}{y^3}z - 3xy + 2{x^2}{y^2} - x\) چند است؟
درجه x برابر ۳ است.
مثال
چند جمله ای زیر را نسبت به توان های نزولی a (از بزرگ به کوچک) مرتب کنید.
\({a^3}b{\rm{ }} - 3 + 2{a^3}{b^2} - 5ab{\rm{ }}\)
\({a^3}b{\rm{ }} - 3 + 2{a^3}{b^2} - 5ab{\rm{ }} = 2{a^3}{b^2} + {a^2}b - 5ab - 3\)
تهیه کننده: مسعود زیرکاری
اتحاد جبری
فصل 5 : عبارت های جبری
اتحاد جبری
اگر دو عبارت جبری به گونه ای باشند که با ازای تمام مقادیر دلخواه برای متغیرها مقدار یکسانی داشته باشد به تساوی جبری آنها اتحاد می گویند.
مثال
آیا \({(x - 2)^2} = {x^2} - 4x + 4\) یک اتحاد است؟ چرا؟
به ازای مقادیر دلخواه امتحان میکنیم اگر دو طرف تساوی یکی شد این تساوی یک اتحاد است.
\(\left\{ \begin{array}{l}x = - 4 \Rightarrow {( - 4 - 2)^2} = {( - 4)^2} - 4( - 4) + 4 \Rightarrow 36 = 36\\\\x = 5 \Rightarrow {(5 - 2)^2} = {5^2} - 4(5) + 4 \Rightarrow 9 = 9\end{array} \right.\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اتحاد مربع دو جمله ای
فصل 5 : عبارت های جبری
اتحاد مربع دو جمله ای
الف) جبری:
\(\left\{ \begin{array}{l}{(a + b)^2} = {a^2} + 2ab + {b^2}\\{(a + b)^2} = {a^2} - 2ab + {b^2}\end{array} \right.\)
ب( کلامی :
(جمله دوم به توان2) +( 2 برابر جمله اول در دوم) + )جمله اول به توان 2) = (جمله دوم + جمله اول)
مثال
حاصل عبارت های جبری زیر را به کمک اتحاد به دست آورید.
\({(a - 2b)^2}\)
\({(a - 2b)^2} = {a^2} - 2(a)(2b) + {(2b)^2} = {a^2} - 4ab + 4{b^2}\)
\({(xy + 3)^2}\)
\({(xy + 3)^2} = {x^2}{y^2} + 2(xy)(3) + {3^2} = {x^2}{y^2} + 6xy + 9\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
اتحاد مزدوج
فصل 5 : عبارت های جبری
اتحاد مزدوج
الف) جبری :
\((a + b)(a - b) = {a^2} - {b^2}\)
ب( کلامی :
(جمله دوم به توان 2) - (جمله اول به توان 2) = (جمله دوم - جمله اول) × (جمله دوم + جمله اول)
مثال
حاصل عبارت های جبری زیر را به کمک اتحاد به دست آورید.
\((a - 3b)(a + 3b)\)
\((a - 3b)(a + 3b) = {a^2} - {(3b)^2} = {a^2} - 9{b^2}\)
\(\left( {2x + \frac{y}{2}} \right)\left( {2x - \frac{y}{2}} \right)\)
\(\left( {2x + \frac{y}{2}} \right)\left( {2x - \frac{y}{2}} \right) = {(2x)^2} - {(\frac{y}{2})^2} = 4{x^2} - \frac{{{y^2}}}{4}\)
حاصل عبارت جبری زیر را به کمک اتحاد به دست آورید.
\(\left( {2a - 3} \right)(2a + 4)\)
\(\left( {2a - 3} \right)(2a + 4) = {(2a)^2} + ( - 3 + 4)(2a) + ( - 3 \times 4) = 4{a^2} + 2a - 12\)
تهیه کننده: مسعود زیرکاری
تجزیه عبارت جبری
فصل 5 : عبارت های جبری
تجزیه عبارت جبری
نوشتن یک عبارت جبری به صورت حاصل ضرب چند عبارت دیگر را تجزیه می گویند.
روشهای تجزیه :
الف) فاکتور گیری
ب) با استفاده از اتحادها
فاکتور گیری
برای فاکتور گیری مراحل زیر را انجام می دهیم :
۱) (ب.م.م) ضرایب را تعیین میکنیم
۲) حروف مشترک با توان کمتر را انتخاب می کنیم
۳) (ب.م.م) و حروف مشترک را به عنوان فاکتور می گیریم
۴) تمام جملات را بر عامل فاکتور تقسیم کرده و جواب را داخل پرانتز می نویسیم
مثال
عبارت های جبری زیر را تجزیه کنید.
\(18xy - 12y\)
\(18xy - 12y = 6y(3x - 2)\)
\(16{a^{2b}} + 4a{b^2} - {y^4}\)
\(16{a^{2b}} + 4a{b^2} - {y^4} = {(2x + {y^2})^2}\)
تجزیه به کمک اتحاد مربع
۱) تعداد جملات ۳ جمله باشد
۲) جمله اول و جمله سوم جذر دقیق داشته باشند
مثال
عبارت های جبری زیر را تجزیه کنید.
\({a^2} - 6a + 9\)
\({a^2} - 6a + 9 = {(a - 3)^2}\)
\(4{x^2} + 4x{y^2} + {y^4}\)
\(4{x^2} + 4x{y^2} + {y^4} = {(2x + {y^2})^2}\)
تجزیه به کمک اتحاد جمله مشترک
۱) تعداد جملات ۳ جمله باشد
۲) جمله اول و جمله سوم جذر دقیق نداشته باشند
۳) ضریب x حاصل جمع و عدد آخر حاصل ضرب دو عدد را نشان می دهد
مثال
عبارت های جبری زیر را ساده کنید.
\({x^2} - 5x + 6\)
\({x^2} - 5x + 6 = (x - 3)(x - 2)\)
\({x^2} - 1x - 12\)
\({x^2} - 1x - 12 = (x - 4)(x + 3)\)
تجزیه به کمک اتحاد مزدوج
۱) تعداد جملات ۲ جمله باشد
۲) جملات اول و دوم جذر دقیق داشته باشند
۳) بین جملات علامت منفی باشد
مثال
عبارت های جبری زیر را ساده کنید.
\({a^2} - 9\)
\({a^2} - 9 = (a - 3)(a + 3)\)
\({x^4} - 16\)
\({x^4} - 16 = ({x^2} - 4)({x^2} + 4)\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نامعادله
فصل 5 : عبارت های جبری
نامعادله
جواب های نامعادله مقادیری از متغیر هستند که به ازای آنها نامساوی برقرار است. همه ی جواب های نامعادله مجموعه جواب آن گفته می شود.
1 اگر به طرفین یک نا مساوی عدد اضافه یا عددی کم شود جهت نابرابری عوض نمی شود :
\(a < b \Rightarrow a + c < b + c\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,a < b \Rightarrow a - c < b - c\)
2 اگر طرفین یک نا مساوی در عدد مثبت ضرب یا بر عدد مثبت تقسیم کنیم جهت نابرابری عوض نمی شود:
\(a\rangle b \Rightarrow ac\rangle bc\,\,\,\,\,\,,\,\,\,\,\,\,a\rangle b \Rightarrow \frac{a}{c}\rangle \frac{b}{c}\)
3 اگر طرفین یک نا مساوی در عدد منفی ضرب یا بر عدد منفی تقسیم کنیم جهت نابرابری عوض می شود :
\(a < b \Rightarrow ac\rangle bc\,\,\,\,\,,\,\,\,\,\,a < b \Rightarrow \frac{a}{c}\rangle \frac{b}{c}\)
حل نامعادله
همانند یک معادله حل میشود با این تفاوت که اگر در اخر نامعادله ضریب مجهول عدد منفی باشد جهت نامعادله عوض می شود.
مثال
مجموعه جواب نامعادله ی زیر را به دست آورده و روی محور اعداد نمایش دهید.
\(4(x - 1) \le 5x - 2\)
\(4(x - 1) \le 5x - 2 \Rightarrow 4x - 4 \le 5x - 2 \Rightarrow 4x - 5x \le 2 \Rightarrow - x \le 2 \Rightarrow x \ge - 2\)
در مسایل مربوط به نابرابری به جای کلمه حداکثر از علامت\( \le \)و به جای کلمه حداقل از علامت\( \ge \)استفاده می کنیم.
مثال
عبارت زیر را به صورت جبری بنویسید :
" مجموع دو برابر عددی با قرینه سه برابر عدد دیگر حداکثر ۹ است. "
\(2x + ( - 3y) \le - 9\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
معادله خط
فصل 6 : خط و معادله های خطی
معادله خط
رابطه ای است که بین نقاط تشکیل دهنده یک خط وجود دارد.
1 فرم کلی معادله خط به صورت y = ax + b) ( می باشد.
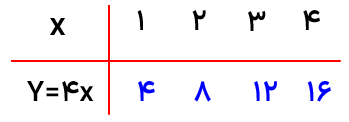
2 در صورتی که نمودار رابطه ی بین دو مقدار به صورت خط راست باشد. آن دو مقدار با هم رابطه خطی دارند.
مثال
آیا رابطه بین یک ضلع مربع و محیط مربع رابطه ی خطی است؟ چرا؟
بله چون افزایش یک ضلع مربع با افزایش محیط مربع یک مقدار ثابت است .(ضلع مربع را X و محیط مربع را y در نظر میگیریم پس خواهیم داشت :x 4=y )
مثال
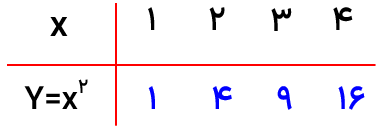
آیا رابطه بین یک ضلع مربع و مساحت مربع رابطه ی خطی است؟ چرا؟
خیر. چون افزایش یک ضلع مربع با افزایش مساحت مربع مقدار ثابتی نیست. (ضلع مربع را x و مساحت مربع را y در نظر میگیریم بنابرین خواهیم داشت :\(y = {x^2}\) )
انواع معادله خط
۱) مبدا گذر (فرم کلی : y=ax )
۲) غیر مبدا گذر (فرم کلی : y = ax + b)
۳) خطوط موازی با محور (فرم کلی : m , x = n = y)
تهیه کننده: مسعود زیر کاری
ترسیم خط در دستگاه مختصات
فصل 6 : خط و معادله های خطی
رسم یک خط
برای رسم یک خط در دستگاه مختصات نیاز به مختصات دو نقطه است.
اگر در فرم کلی استاندارد معادله خط عدد قبل از x عدد صحیح باشد در جدول به جای اعداد ( 0 و 1) قرار می دهیم ، و عدد قبل از x عدد کسری باشد به جای x اعداد ( صفر و مخرج کسر ) قرار می دهیم.
مثال
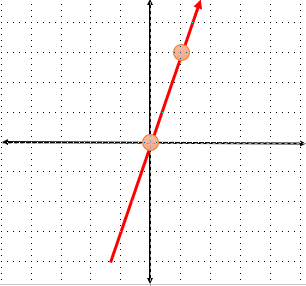
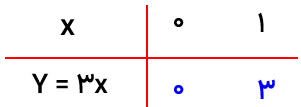
معادله خط y=3xرا در دستگاه مختصات رسم کنید.
خط مبدا گذر:
مثال
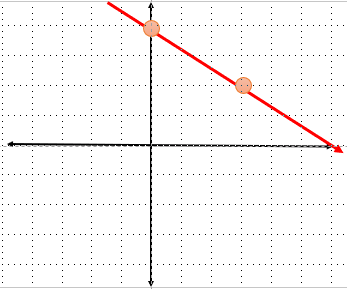
معادله خط \(y = - \frac{2}{3}x + 4\) را در دستگاه مختصات رسم کنید.
خط غیر مبدا گذر:
مثال
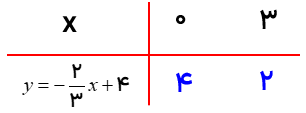
معادلات خط ۲- = y و ۴ = x را در دستگاه مختصات رسم کنید.
برای رسم این خط ها نیاز به جدول نیست. فقط کافی است هر نقطه داده شده را در دستگاه مختصات مشخص کرد سپس خطی موازی با محور از روی آن نقطه رسم کرد.
خط موازی با محور
زاویه ی بین خطوط موازی با محور ۹۰ درجه است.
شرط این که نقطه روی یک خط قرار گیرد این است که مختصات آن نقطه در معادله خط صدق کند که برای این کار دو روش وجود دارد:
۱ روش تحلیلی (جایگزینی مختصات نقطه در معادله خط)
۲ روش ترسیمی
مثال
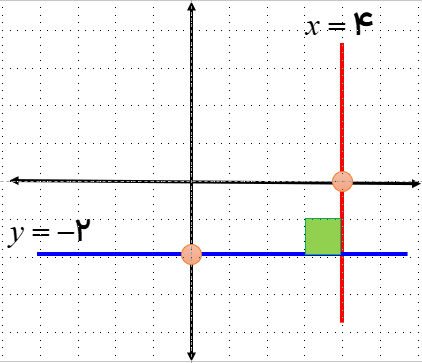
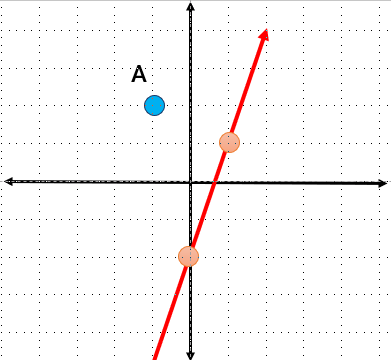
آیا نقطه ی \(A = \left[ \begin{array}{l} - 1\\2\end{array} \right]\) روی خط ۲ – ۳x = y قرار دارد؟
روش تحلیلی :قرار ندارد چون دو طرف تساوی برابر نیست :
\((x = - 1\,,\,y = 2) \Rightarrow 2 = 3( - 1) - 2 \Rightarrow 2 \ne - 5\)
روش ترسیمی : خط داده شده را در دستگاه مختصات رسم کرده سپس نقطه A را نیز در دستگاه مختصات مشخص می کنیم :
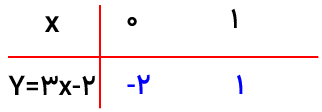
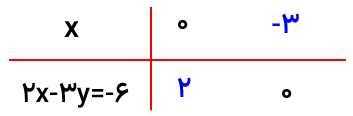
برای رسم معادلات خطی که به صورت (ax + by = c) هستند. در جدول یک بار به جای x و یک بار به جای yصفر قرار می دهیم
مثال
معادله خط ۶ = y۳x - ۲ را در دستگاه مختصات رسم کنید.
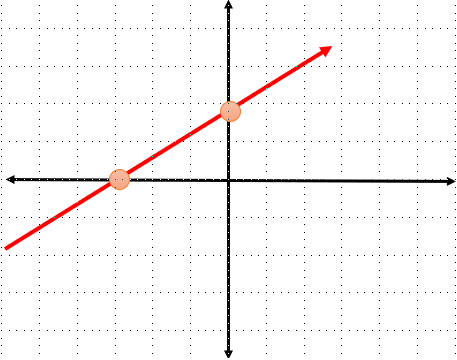
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
شیب خط و عرض از مبدا
فصل 6 : خط و معادله های خطی
شیب خط
زاویه ای بین سمت راست محور طول ها با خط داده شده را می گویند.
عرض از مبدا
نقطه ای که خط داده شده محور عرض ها را در آن نقطه قطع میکند را عرض از مبدا می گویند.
1 در فرم کلی معادله خط (y=ax + b ) ضریب x یعنی عدد a شیب خط و عدد b عرض از مبدا نام دارد.
مانند : در معادله خط \(y = - \frac{1}{4}x + 1\) (عدد شیب خط : \( - \frac{1}{3}\) ) و عدد (عرض از مبدا : ۱) می باشد.
2 برای به دست آوردن شیب خط و عرض مبدا باید معادله خط به فرم کلی (y= ax + b)مرتب شود.
مثال
شیب خط و عرض از مبدا معادله های خطی زیر را به دست آورید.
الف) \( - 5x + 2y = - 6\)
\(2y = 5x - 6 \Rightarrow \frac{{2y}}{2} = \frac{{5x}}{2} - \frac{6}{2} \Rightarrow y = \frac{5}{2}x - 3\)
(عرض از مبدا : -3 و شیب خط ب خط :\(\frac{5}{2}\))
ب) \(2y = - 4x\)
\(\frac{{2y}}{2} = \frac{{ - 4x}}{2} \Rightarrow y - 2x\)
) عرض از مبدا : ۰ و شیب خط: -2 )
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
طول از مبدا
فصل 6 : خط و معادله های خطی
طول از مبدا
نقطه ای که خط داده شده محور طول ها را در آن نقطه قطع میکند را طول از مبدا می گویند.
برای به دست آوردن طول از مبدا در معادله خط به جای y صفر قرار می دهیم.
مثال
طول از مبدا معادله خط \(\frac{2}{3}x - \frac{1}{4}y = - 5\) را به دست آورید.
\(y = 0 \Rightarrow \frac{2}{3}x - \frac{1}{4}(0) = - 5 \Rightarrow \frac{2}{3}x = - 5 \Rightarrow x = \frac{{ - 5}}{{\frac{2}{3}}} = - \frac{{15}}{2} \Rightarrow x = - \frac{{15}}{2}\)
1 دو خط در صورتی موازی هستند که شیب دو خط برابر باشند . مانند :\(y = - 3x\,,\,y = - 3x + 5\)
2 دو خط در صورتی بر هم عمود هستند که شیب دو خط قرینه و معکوس یکدیگر باشند یا حاصل ضرب دو شیب خط برابر با عدد ۱ - شود. مانند : \(y = 2x + 3\,,\,y = - \frac{1}{2}x - 2\)
مثال
معادله خطی بنویسید که با خط ۵ =y ۳ - X موازی و از نقطه ی \(A = \left[ \begin{array}{l}0\\ - 2\end{array} \right]\) بگذرد.
ابتدا معادله خط را مرتب کرده تا شیب خط مشخص شود:
\(\begin{array}{l} - 3y = - x + 5 \Rightarrow \frac{{ - 3y}}{{ - 3}} = - \frac{x}{{ - 3}} + \frac{5}{{ - 3}} \Rightarrow \frac{1}{3}x - \frac{5}{3} \Rightarrow a = \frac{1}{3}\\(a = \frac{1}{{3\,}}\,\,\,,\,\,\,\,b = - 2)\\\\y = ax + b \Rightarrow y = \frac{1}{3}x - 2\end{array}\)
معادله خط جدید:\(y = \frac{1}{3}x - 2\)
مثال
معادله خطی بنویسید که با خط\(y = - \frac{1}{5} + 2\) عمود باشد و از نقطه ی \(B = \left[ \begin{array}{l} - 1\\2\end{array} \right]\) بگذرد.
شیب خط مشخص است پس باید عرض از مبدا را به دست آوریم :
\(\begin{array}{l}(a = 5\,\,,\,\,x = - 1\,\,\,,\,\,\,y = 2)\\\\y = ax + b \Rightarrow 2 = 5( - 1) + b \Rightarrow b = 7\\(b = 7)\\\\y = ax + b \Rightarrow y = 5x + 7\end{array}\)
معادله خط جدید:\(y = 5x + 7\)
برای به دست آوردن شیب خطی که از دو نقطه میگذرد از رابطه ی زیر استفاده می کنیم :
معادله خطی بنویسید که از نقاط \(B = \left[ \begin{array}{l} - 1\\4\end{array} \right]\,\,\,,\,\,\,A = \left[ \begin{array}{l}2\\3\end{array} \right]\) بگذرد.
\(\begin{array}{l}a = \frac{{4 - 3}}{{ - 1 - 2}} = - \frac{1}{3}\,\,\,\,,\,\,\,\,(x = 2\,,\,y = 3)\\\\y = ax + b \Rightarrow y = - \frac{1}{3}x + \frac{{11}}{3}\end{array}\)
معادله خط جدید:\(y = - \frac{1}{3}x + \frac{{11}}{3}\)
معادله خط محور طول ها (y=0) و معادله خط محور عرض ها ( 0= x (و معادله خط نیمساز ربع اول و سومx) =y ) و معادله خط نیمساز ربع دوم و چهارم y =-x) ( می باشد.
تهیه کننده: مسعود زیرکاری
دستگاه معادلات خطی
فصل 6 : خط و معادله های خطی
دستگاه معادلات خطی
برای حل دستگاه معادلات خطی از روش های زیر می توان استفاده کرد :
1- روش حذفی:
در این روش یکی از متغیرها را حذف کرده سپس با جایگزینی متغیر دوم به دست می آید.
مثال
دستگاه معادلات دو مجهولی زیر را حل کنید.
\(\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4 + y = - 7\end{array} \right.\)
\(\begin{array}{l}2x + 3(1) = 7 \Rightarrow 2x = 4 \Rightarrow x = 2\\\\\mathop {}\limits^{2 \times } \,\,\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4 + y = - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4x + 6y = 14\\\\ - 4 + y = - 7\end{array} \right. \Rightarrow 7y = 7 \Rightarrow y = 1\end{array}\)
جواب دستگاه دو مجهولی: \(A = \left[ \begin{array}{l}2\\1\end{array} \right]\)
2- روش جایگزینی( تبدیلی):
در این روش یکی از معادلات را بر حسب یک متغیر مرتب کرده و مقدار آن را در معادله دوم قرار می دهیم.
مثال
دستگاه معادلات دو مجهولی زیر را حل کنید. (روش جایگزینی)
\(\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4x + y = - 7\end{array} \right.\)
ابتدا معادله اول را برحسب xمرتب می کنیم سپس مقدار xرا در معادله پایین قرار می دهیم.
\(\begin{array}{l}\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4x + y = - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2x = - 3y + 7 \Rightarrow x = - \frac{3}{2}y + \frac{7}{2}\\ - 4( - \frac{3}{2}y + \frac{7}{2}) + y = - 7 \Rightarrow 6y - 14 + y = - 7 \Rightarrow 7y = 7 \Rightarrow y = 1\end{array} \right.\\\\x = - \frac{3}{2}(1) + \frac{7}{2} \Rightarrow x = - \frac{3}{2} = \frac{7}{2} = \frac{4}{2} = 2 \Rightarrow x = 2\end{array}\)
جواب دستگاه دو مجهولی :\(A = \left[ \begin{array}{l}2\\1\end{array} \right]\)
برای حل بعضی از مسایل میتوان از دستگاه دو مجهولی استفاده کرد و به یکی از روش های آن را حل کرد.
سن برادر علی ۳ برابر سن او است،و اختلاف سن آنها ۱۸ سال است. سن هر یک را به دست آورید. (به روش جایگزینی)
)سن برادر علی را X و سن علی را y فرض می کنیم.(
\(\begin{array}{l}\left\{ \begin{array}{l}x = 3y\\\\x - y = 18\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 3y\\\\3y - y = 18 \Rightarrow 2y = 18 \Rightarrow y = 9\end{array} \right.\\\\x = 3(9) = 27 \Rightarrow x = 27\end{array}\)
علی9 سال و برادرش 27 سال دارد.
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
عبارت گویا
فصل 7 : عبارت های گویا
عبارت گویا
کسری است که صورت و مخرج آن چند جمله ای باشند.
مانند :
\(\frac{{4{x^2} - 1}}{{2x + 3}},\frac{{\sqrt 5 x}}{2},\frac{{x - 3}}{x}\)
1 عبارتی که متغیر آن توان منفی یا زیر رادیکال یا داخل قدر مطلق یا در مخرج کسر یا در توان باشد. گویا نیست.
مانند :\(\left| {x - 2} \right|,\frac{{{x^y}}}{3},\frac{{4 - \sqrt x }}{{3x}}\)
2 عبارت گویا به ازای مقادیری که مخرج کسر را صفر می کند تعریف نشده است.
مثال
عبارت های گویا زیر به ازای چه مقادیری از مخرج کسر تعریف نشده است؟
\(\frac{{{x^2} - 5}}{{2x - 4}}\)
(مخرج کسر را مساوی صفر قرار داده تا مقادیر تعریف نشده مشخص شوند)
\(\frac{{{x^2} - 5}}{{2x - 4}} \Rightarrow 2x - 4 = 0 \Rightarrow 2x = 4 \Rightarrow x = 2\)
عبارت گویا به ازای (۲ = x) تعریف نشده است
\(\frac{{x - 4}}{{{x^2} - 4x}}\)
\(\frac{{x - 4}}{{{x^2} - 4x}} \Rightarrow {x^2} - 4x = 0 \Rightarrow x(x - 4) = 0 \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x - 4 = 0 \Rightarrow x = 4\end{array} \right.\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
ساده کردن عبارت گویا
فصل 7 : عبارت های گویا
ساده کردن عبارت گویا
برای ساده کردن صورت و مخرج را به صورت حاصل ضرب دو یا چند عبارت جبری نوشته سپس عبارت های مساوی را از صورت و مخرج ساده می کنیم.
برای ساده کردن عبارت های گویا از فاکتورگیری و اتحاد استفاده می کنیم.
مثال
عبارت های گویا زیر را ساده کنید.
\(\frac{{{x^2} - 4}}{{{x^2} + 2x}}\)
\(\frac{{{x^2} - 4}}{{{x^2} + 2x}} = \frac{{(x - 2)(x + 2)}}{{x(x + 2)}} = \frac{{(x - 2)}}{x}\)
\(\frac{{{x^2} - 5x + 6}}{{{x^2} - 6x + 9}}\)
\(\frac{{{x^2} - 5x + 6}}{{{x^2} - 6x + 9}} = \frac{{(x - 3)(x - 2)}}{{(x - 3)(x - 3)}} = \frac{{(x - 2)}}{{(x - 3)}}\)
تهیه کننده: مسعود زیرکاری
ضرب و تقسیم عبارت های گویا
فصل 7 : عبارت های گویا
ضرب عبارت های گویا
در ضرب عبارت های گویا ابتدا ساده میکنیم سپس صورت در صورت و مخرج در مخرج ضرب می کنیم.
تقسیم عبارت های گویا
ابتدا تقسیم را به ضرب تبدیل میکنیم یعنی کسر اولی را در معکوس کسر دومی ضرب می کنیم.
مثال
حاصل ضرب و تقسیم عبارت های گویا زیر را به دست آورید.
\(\frac{{x + 5}}{{3x + 6}} \times \frac{{x + 2}}{{{x^2} - 25}}\)
\(\frac{{x + 5}}{{3x + 6}} \times \frac{{x + 2}}{{{x^2} - 25}} = \frac{{(x + 5)}}{{3(x + 2)}} \times \frac{{(x + 2)}}{{(x - 5)(x + 5)}} = \frac{1}{{3(x - 5)}}\)
\(\frac{{{x^2} - 2x - 15}}{{x + 3}} \div \frac{{{x^2} - x - 12}}{{2x + 6}}\)
\(\frac{{{x^2} - 2x - 15}}{{x + 3}} \div \frac{{{x^2} - x - 12}}{{2x + 6}} = \frac{{(x - 5)(x + 3)}}{{(x + 3)}} \times \frac{{2(x + 3)}}{{(x - 4)(x + 4)}} = \frac{{2(x + 5)}}{{(x - 4)}}\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
جمع و تفریق عبارت های گویا
فصل 7 : عبارت های گویا
جمع و تفریق عبارت های گویا
بین مخرج ها مخرج مشترک (ک.م.م) مخرج ها را انتخاب می کنیم.
مثال
حاصل جمع و تفریق های زیر را به دست آورید.
\(\frac{{2x + 3}}{{x + 1}} + \frac{{x - 4}}{{x - 2}}\)
\(\frac{{2x + 3}}{{x + 1}} + \frac{{x - 4}}{{x - 2}} = \frac{{(2x + 3)(x - 2) + (x - 4)(x + 1)}}{{(x + 1)(x - 2)}} = \frac{{3{x^2} - 4x - 10}}{{(x + 1)(x - 2)}}\)
\(\frac{{x - 1}}{{x - 3}} - \frac{{x + 5}}{{{x^2} - 9}}\)
\(\frac{{x - 1}}{{x - 3}} - \frac{{x + 5}}{{{x^2} - 9}} = \frac{{(x - 1)(x + 3) - (x + 5)}}{{(x - 3)(x + 3)}} = \frac{{{x^2} + x - 8}}{{(x - 3)(x + 3)}}\)
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
ساده کردن عبارت های مرکب
فصل 7 : عبارت های گویا
ساده کردن عبارت های مرکب
عبارت صورت کسر و عبارت مخرج کسر را جداگانه جواب داده و در آخر حاصل عبارت صورت را برحاصل عبارت مخرج تقسیم می کنیم.
مثال
حاصل عبارت زیر را به ساده ترین صورت بنویسید.
\(\frac{{\frac{3}{{{x^2}}} - \frac{4}{x} + 1}}{{1 - \frac{6}{{{x^2}}} - \frac{1}{x}}}\)
\(\frac{{\frac{3}{{{x^2}}} - \frac{4}{x} + 1}}{{1 - \frac{6}{{{x^2}}} - \frac{1}{x}}} = \frac{{\frac{{3 - 4x + {x^2}}}{{{x^2}}}}}{{\frac{{{x^2} - 6 - x}}{{{x^2}}}}} = \frac{{(x - 3)(x - 1)}}{{{x^2}}} \times \frac{{{x^2}}}{{(x - 3)(x + 2)}} = \frac{{(x - 1)}}{{(x + 2}}\)
تقسیم یک جمله ای بر یک جمله ای
۱) علامت ها در هم ضرب شده
۲) اعداد با هم ساده میشوند
۳) حروف (متغیرها) با هم ساده میشوند
در ساده کردن متغیرها از قاعده تقسیم اعداد توان دار استفاده میشود
مثال
عبارت گویا زیر را ساده کنید.
\(\frac{{ - 18{x^5}{y^2}{z^4}}}{{12{x^3}{y^3}{z^4}}}\)
\(\frac{{ - 18{x^5}{y^2}{z^4}}}{{12{x^3}{y^3}{z^4}}} = \frac{{ - 18}}{{12}} \times \frac{{{x^5}}}{{{x^3}}} \times \frac{{{y^2}}}{{{y^3}}} \times \frac{{{z^4}}}{{{z^4}}} = - \frac{{3{x^2}}}{{2y}}\)
تقسیم چند جمله ای بر یک جمله ای
تک تک جملات صورت کسر را بر مخرج کسر تقسیم می کنیم.
مثال
عبارت گویا زیر را ساده کنید.
\(\frac{{4{x^5} - 6{x^3} + 12x}}{{2x}}\)
\(\frac{{4{x^5} - 6{x^3} + 12x}}{{2x}} = \frac{{4{x^5}}}{{2x}} - \frac{{6{x^3}}}{{2x}} + \frac{{12x}}{{2x}} = 2{x^4} - 3{x^2} + 6\)
تقسیم چند جمله ای بر چند جمله ای
برای این تقسیم مراحل زیر را به ترتیب انجام می دهیم :
1) ابتدا مقسوم و مقسوم علیه را به شکل استاندارد یعنی از بیشترین توان به کمترین توان می نویسیم.
۲) اولین جمله ی مقسوم را بر اولین جمله ی مقسوم علیه تقسیم کرده و حاصل را در خارج قسمت می نویسیم.
3)خارج قسمت را در تک تک جملات مقسوم علیه ضرب کرده و حاصل را زیر عبارت مقسوم نوشته و دو عبارت را از هم کم می کنیم.
۴) برای چند جمله ای به دست آمده مراحل ۲ و ۳ را تکرار کنیم و این تکرار را تا جایی ادامه میدهیم که درجه باقی مانده از درجه مقسوم علیه کمتر شود.
مثال
خارج قسمت و باقی مانده تقسیم \(4x - {x^2} + 7 + 2{x^2} \div x - 2\) زیر را به دست آورید.
مرحله اول )استاندارد کردن عبارت) \(4x - {x^2} + 7 + 2{x^2} = {x^2} - 4x + 7\)
مرحله دوم )تقسیم مقسوم بر مقسوم عليه) \(\frac{{{x^2}}}{x} = x\)
مرحله سوم (حاصل ضرب خارج قسمت در مقسوم علیه) \(x(x - 2x) = {x^2} - 2x\)
رابطه تقسیم : \((x - 2)(x + 6) + 19 = {x^2} + 4x + 7\)
اگر در تقسیم دو عبارت باقی مانده صفر .شود مقسوم بر مقسوم علیه بخش پذیر است.
مثال
مقدار a طوری بیابید که چند جمله ای ۳ - X - x + a بر ۵ – x۲ بخش پذیر باشد.
بخش پذیر بودن یعنی باقی مانده تقسیم صفر شود :\(a + 7 = 0 \Rightarrow a = - 7\)
تهیه کننده: مسعود زیرکاری
انواع حجم
فصل 8 : حجم و مساحت
حجم
مقدار فضایی را که یک جسم اشغال میکند حجم (گنجایش) نام دارد و حجم را با حرف انگلیسی (v) نشان می دهند.
انواع حجم
۱) حجم منشوری
۲) حجم هرمی یا مخروطی
۳) حجم کروی
دایره
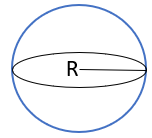
مجموعه نقاطی از صفحه که فاصله تمام نقاط از یک نقطه به نام (مرکز دایره) به یک اندازه باشد. به این فاصله نقاط صفحه تا مرکز دایره (شعاع دایره ) می گویند .
دایره را به اختصار به صورت C(O,R) نشان می دهند.
C=دایره O=مرکز R=شعاع
کره
مجموعه نقاطی از فضا که فاصله تمام نقاط از یک نقطه به نام مرکز کره به یک اندازه باشد به این فاصله نقاط صفحه تا مرکز دایره شعاع کره می گویند.
مانند :
کره زمین و توپ
فرمول مساحت کره : \(S = 4\pi {r^2}\)
فرمول حجم کره :\(v = \frac{4}{3}\pi {r^3}\)
مثال
حجم و مساحت کره با قطر ۴ سانتی متر را به دست آورید.
\(\begin{array}{l}R = 4 \div 2 = 2\\\\\left\{ \begin{array}{l}v = \frac{4}{3}\pi {r^2} = \frac{4}{3} \times 3/14 \times {2^3} = 50/24\\\\S = 4\pi {r^2} = 4 \times 3/14 \times {2^2} = 50/24\end{array} \right.\end{array}\)
مثال
نسبت عددی حجم کره به مساحت کره چند است.
\(\frac{v}{s} = \frac{{\frac{4}{3}\pi {r^2}}}{{4\pi {r^2}}} = \frac{1}{3}r\)
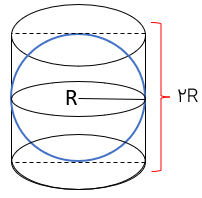
اگر کره به طور کامل داخل استوانه قرار گیرد می گوییم کره بر استوانه محاط شده و استوانه بر کره محیط شده است.
مثال
کره ای در استوانه ای به قطر ۶ سانتی متر محاط شده است :
الف) حجم کره را به دست آورید.
\(\begin{array}{l}R = 6 \div 2 = 3cm\\\\v = \frac{4}{3}\pi {r^2} = \frac{4}{3} \times 3/14 \times {3^3} = 113/04c{m^3}\end{array}\)
ب) حجم استوانه را به دست آورید.
\(v = s \times h = (3 \times 3 \times 3/4) \times 6 = 169/56c{m^3}\)
ج) حجم فضای بین کره و استوانه را به دست آورید.
\(169/56 - 113/04 = 56/52c{m^3}\)
1 از دوران نیم دایره حول قطر کره حاصل می شود.
2 از دوران ربع دایره حول شعاع نیم کره حاصل می شود.
3 برای به دست آوردن حجم نیم کره می توان از رابطه ی \(v = \frac{2}{3}\pi {r^3}\) استفاده کرد.
مثال
حجم حاصل از دوران ربع دایره حول شعاع ۴ سانتی متر را به دست آورید. (بر حسب\(\pi \))
)از دوران ربع دایره حول شعاع نیم کره حاصل می شود)
\(v = \frac{2}{3}\pi {r^3} = \frac{2}{3}\pi \times {4^3} = 42/66\)
اگر شعاع کره را n برابر کنیم مساحت کره \({n^2}\) و حجم کره \({n^3}\) برابر خواهد شد.
مثال
اگر شعاع کره ای را ۴ برابر کنیم مساحت و حجم کره چند برابر خواهد شد؟
\(\begin{array}{l}s = {n^2} = {4^2} = 16\\\\v = {n^3} = {4^3} = 64\end{array}\)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
هرم
فصل 8 : حجم و مساحت
هرم
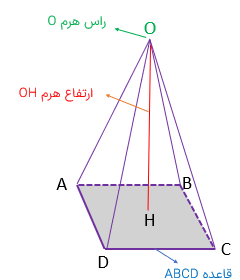
هرم شکل فضایی که سطح جانبی آن مثلث و وجه زیرین (قاعده( آن چند ضلعی محدب باشد.
به فاصله راس هرم تا قاعده ارتفاع هرم می گویند.
حجم هرم
الف( کلامی
ارتفاع × مساحت قاعده ×\(\frac{1}{3}\) = حجم هرم
ب جبری :
\(v = \frac{1}{3}s.h\)
مثال
حجم هرم مربع القاعده ای به ضلع ۵ سانتی متر و ارتفاع ۶ سانتی متر را به دست آورید.
\(v = \frac{1}{3}s.h = \frac{1}{3} \times (5 \times 5) \times 6 = 50c{m^3}\)
) خودش × یک ضلع = s مربع)
مثال
قاعده لوزی با قطرهای ۶ و ۸ سانتی متر است. اگر ارتفاع هرم ۵ سانتی متر باشد حجم هرم چند سانتی متر مکعب است؟
(2÷حاصل ضرب دو قطر = لوزیs )
\(v = \frac{1}{3}s.h = \frac{1}{3} \times \left( {\frac{{6 \times 8}}{2}} \right) \times 5 = 40c{m^3}\)
اگر دو هرم دارای قاعده های هم مساحت و ارتفاع یکسان باشند. دارای حجم برابر هستند.
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم
جزوه جامع علوم تجربی نهم
جزوه جامع مطالعات اجتماعی نهم
جزوه جامع عربی نهم
جزوه جامع فارسی نهم
جزوه جامع نگارش نهم
جزوه جامع زبان انگلیسی نهم
جزوه جامع کتاب کار انگلیسی نهم
جزوه جامع آمادگی دفاعی نهم
جزوه جامع پیام های آسمانی نهم
جزوه جامع آموزش قرآن نهم
جزوه جامع کار و فناوری نهم
مخروط
فصل 8 : حجم و مساحت
مخروط
شکلی شبیه ای هرم منتظم که قاعده آن دایره و پای ارتفاع مخروط مرکز دایره باشد.
حجم مخروط
الف( کلامی :
ارتفاع × مساحت قاعده ×\(\frac{1}{3}\) = حجم مخروط
ب( جبری :
\(v = \frac{1}{3}s.h = \frac{1}{3}\pi {r^2}h\)
مثال
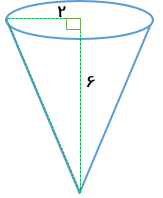
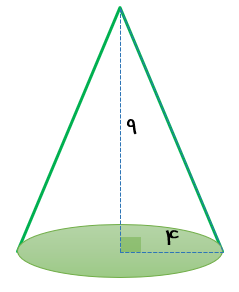
حجم مخروط زیر را حساب کنید.
\(v = \frac{1}{3}s.h = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {2^2} \times 6 = 25/12c{m^3}\)
مثال
گنجایش مخروطی ۴۷۱۰۰ لیتر است. اگر شعاع قاعده ۳ متر باشد ارتفاع مخروط چند متر است؟
هر متر مکعب ۱۰۰۰ لیتر است.
\(47100 \div 1000 = 47/1\,\,{m^3}\) حجم مخروط
\(v = \frac{1}{3}\pi {r^2}h \Rightarrow 47/1 = \frac{1}{3} \times 3/14 \times {3^2} \times h \Rightarrow h = \frac{{47/1}}{{9/42}} = 5\,\,m\)
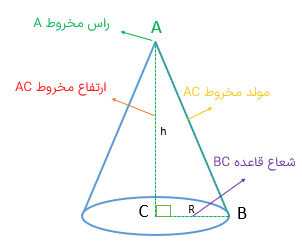
از دوران مثلث قائم الزاویه حول یک ضلع قائم آن مخروط حاصل میشود ضلعی که دوران روی آن انجام شده است ارتفاع مخروط و ضلع دیگر شعاع قاعده نام دارد.
مثال
مثلث قائم الزاویه با اضلاع قائم ۴ و ۹ سانتی متر را روی ضلع بزرگتر دوران داده ایم حجم شکل حاصل چند سانتی متر مکعب است؟
\(v = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {4^2} \times 9 = 150/72c{m^3}\)
مثلث قائم الزاویه ABC را روی حول ضلع AB دوران داده.ایم حجم شکل حاصل را به دست آورید.
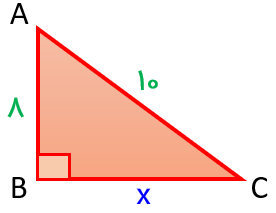
شعاع قاعده\({x^2} = {10^2} - {8^2} = 100 - 64 = 36 \Rightarrow x = 6\) :رابطه فیثاغورس
\(v = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {6^2} \times 8 = 301/44c{m^3}\)
1 از دوران مستطیل و مربع حول یک ضلع آن استوانه تشکیل می شود.
2 مساحت جانبی و مساحت کل استوانه از رابطه های زیر به دست می آید :
\( \Rightarrow s = p \times h\) ارتفاع × محیط قاعده = مساحت جانبی
Sدو قاعده + S جانبی = S کل\( \Rightarrow \)مساحت دو قاعده + مساحت جانبی = مساحت کل
نسبت حجم به مساحت کل استوانه ای را به دست آورید که شعاع قاعده آن a و ارتفاع آن b باشد.
\(v = s \times h = \left( {a \times a \times \pi } \right) \times b = \pi {a^2}b\)
جانبی \(s = p \times h = \left( {2 \times a \times \pi } \right) \times b = 2\pi ab\)
S \( = 2\pi ab + 2{a^2}\pi = 2\pi a\left( {b + a} \right)\) دو قاعده + S جانبی = S کل
\(\frac{v}{s} = \frac{{\pi {a^2}b}}{{2\pi a\left( {a + b} \right)}} = \frac{{ab}}{{2\left( {a + b} \right)}}\)
تهیه کننده:مسعود زیرکاری