جواب فصل 7 احتمال ریاضی دوازدهم تجربی

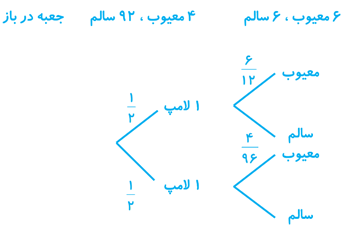
\(\frac{1}{2} \times \frac{6}{{12}} + \frac{1}{2} \times \frac{4}{{96}} = \frac{{48}}{{192}} + \frac{4}{{192}} = \frac{{52}}{{192}} = \frac{{13}}{{48}}\)

\(\begin{array}{l}P(A) = \frac{{20}}{{100}}\;\;,\;\;P(B) = \frac{{50}}{{100}}\;\;,\;\;P(C) = \frac{{30}}{{100}}\\\\P(D|A) = \frac{3}{{100}}\;\;\;,\;\;\;P(D|A) = \frac{5}{{100}}\;\;\;,\;\;\;P(D|C) = \frac{1}{{100}}\\\\P(D) = P(A) \times P(D|A) + P(B) \times P(D|B) + P(C) \times P(D|C)\\\\ = \frac{{20}}{{100}} \times \frac{3}{{100}} + \frac{{50}}{{100}} \times \frac{5}{{100}} + \frac{{30}}{{100}} \times \frac{1}{{100}} = \frac{{6 + 25 + 3}}{{1000}} = 3/4\% \end{array}\)

\(\begin{array}{l}S = \left\{ \begin{array}{l}R\;,\;PPPP\;,\;PPPR\;,\;PPRP\;,\;PRPP\;,\;\\PRRP\;,\;PRPR\;,\;PPRR\;,\;RRRR\end{array} \right\}\\\\A = \left\{ {R\;,\;PPPR\;,\;PPRP\;,\;PRPP} \right\}\\\\P(A) = \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\\\\ + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{2} + \frac{3}{{16}} = \frac{{11}}{{16}}\end{array}\)

\(\begin{array}{l}A = 5\;\;,\;\;B = 2\;\;,\;\;C = 15\;\;,\;\;S = 22\\\\P(Kh|A) = \frac{4}{5}\;\;\;\;\;P(Kh|B) = \frac{9}{{10}}\;\;\;\;\;P(Kh|C) = \frac{1}{2}\\\\P(Kh) = P(A) \times P(Kh|A) + P(B) \times P(Kh|B)\\ + P(C) \times P(Kh|C)\\\\P(Kh) = \frac{5}{{22}} \times \frac{4}{5} + \frac{2}{{22}} \times \frac{9}{{10}} + \frac{{15}}{{22}} \times \frac{1}{2}\\\\ = \frac{2}{{11}} + \frac{9}{{110}} + \frac{{15}}{{44}} = \frac{{40 + 18 + 75}}{{220}} = \frac{{133}}{{220}}\end{array}\)

Q = قبولی

R = ریاضی

T = تجربی

E = انسانی

\(\begin{array}{l}P(Q) = P(R) \times P(Q|R) + P(T) \times P(Q|T)\\ + P(E) \times P(Q|E)\\\\ = \frac{1}{{10}} \times \frac{{45}}{{100}} + \frac{6}{{10}} \times \frac{{10}}{{100}} + \frac{3}{{10}} \times \frac{{30}}{{100}}\\\\ = \frac{{45 + 60 + 90}}{{1000}} = \frac{{195}}{{1000}} = 19/5\% \end{array}\)

الف به این دلیل که به ازای هر 3 دانش آموز از مدرسه A یک دانش آموز از مدرسه B وجود دارد، بنابراین احتمال انتخاب شدن از مدرسه A  برابر \(\frac{3}{4}\) و از مدرسه B \(\frac{1}{4}\) می باشد:

\(P(A) = \frac{3}{4}\;\;\;\;\;\;P(B) = \frac{1}{4}\)

ب

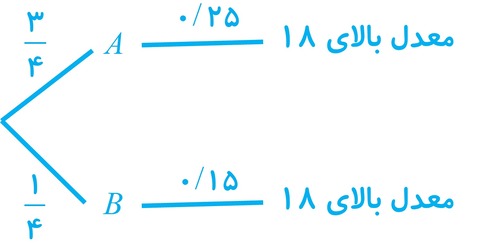
\(P = \frac{3}{4} \times \frac{{25}}{{100}} + \frac{1}{4} \times \frac{{15}}{{100}} = \frac{{75 + 15}}{{400}} = \frac{{90}}{{400}} = \frac{9}{{40}}\)