جواب فصل 1 راهبردهای حل مسئله ریاضی هفتم
تعداد بازدید : 3.13Mپاسخ به تمامی سوالات فصل راهبردهای حل مسئله - حل المسائل فصل 1 راهبردهای حل مسئله - گام به گام 1401 کتاب ریاضی هفتم - گام به گام کتاب ریاضی هفتم مطابق با آخرین تغییرات کتب درسی
راهبرد رسم شکل صفحه 2 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد رسم شکل صفحه 2 درس 1
جواب راهبرد رسم شکل صفحه 2 درس 1 ریاضی هفتم
1- یک باغچهٔ مستطیل شکل به طول 10 و عرض 5 متر داریم. اگر بخواهیم به فاصلهٔ یک متر از ضلع های باغچه، دورتا دور آن را نرده بکشیم، چند متر نرده لازم است؟
ابتدا یک مستطیل رسم کنید.
دور آن به فاصلهٔ یک متر از هر ضلع خط بکشید.
یک مستطیل جدید به وجود می آید. طول و عرض این مستطیل چقدر است؟
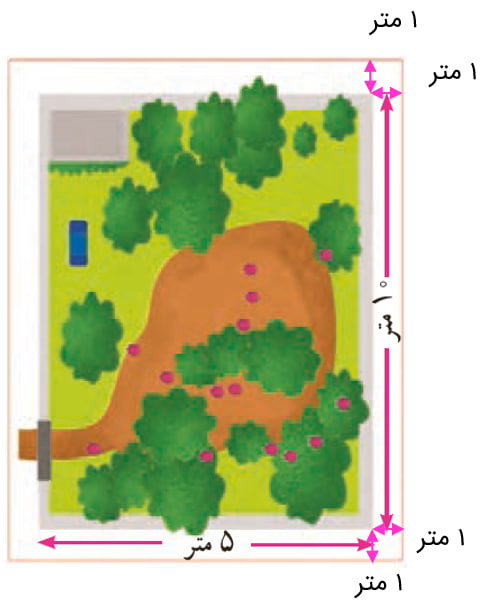
\( = 10 + 1 + 1 = 12\)طول مستطیل جدید
\( = 5 + 1 + 1 = 7\)عرض مستطیل جدید
متر \( = 2 \times (12 + 7) = 38\)محیط مستطیل جدید
2- توپی از ارتفاع 18 متری سطح زمین رها می شود و پس از برخورد با زمین، نصف ارتفاع قبلی خود بالا می آید. این توپ از لحظهٔ رها شدن تا سومین مرتبه ای که به زمین می خورد، چند متر حرکت کرده است؟
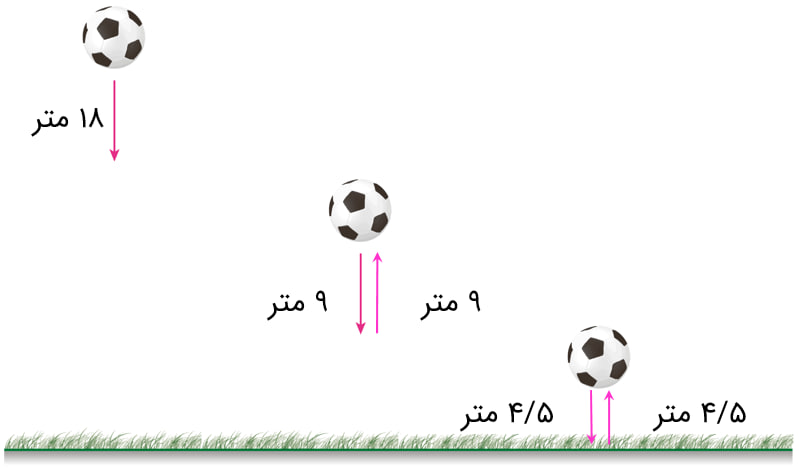
\(18 + 9 + 9 + 4/5 + 4/5 = 45\)متر
3- قورباغه ای می خواهد از یک دیوار بالا برود. او با هر جهش 3 متر بالا می رود و هر بار 2 متر سُر می خورد و پایین می آید. اگر ارتفاع دیوار 9 متر باشد، او با چند جهش به بالای دیوار می رسد؟

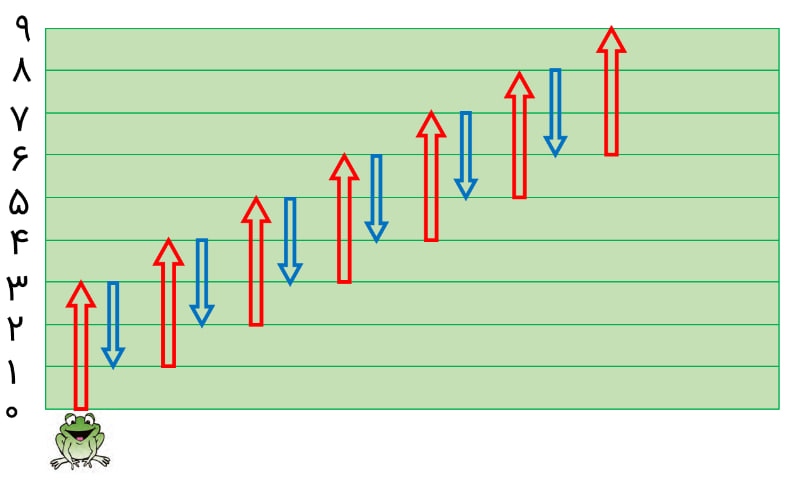
با شمارش پیکان های رو به بالا متوجه می شویم قورباغه با هفت جهش به ارتفاع 9 متر می رسد.

با شمارش پیکان های رو به بالا متوجه می شویم قورباغه با هفت جهش به ارتفاع 9 متر می رسد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
راهبرد الگو سازی صفحه 3 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد الگو سازی صفحه 3 درس 1
جواب راهبرد الگو سازی صفحه 3 درس 1 ریاضی هفتم
1- دو عدد طبیعی پیدا کنید که حاصل ضرب آنها 24 و حاصل جمع آنها کمترین مقدار ممکن باشد. جدول را با نظم و ترتیب کامل کنید.
1- کوچک ترین عدد طبیعی چیست؟
عدد 1
2- حاصل ضرب آن در چه عددی 24 می شود؟
عدد 24
3- اکنون عدد طبیعی بعدی را در نظر بگیرید و به همین ترتیب عددها را پیدا کنید.
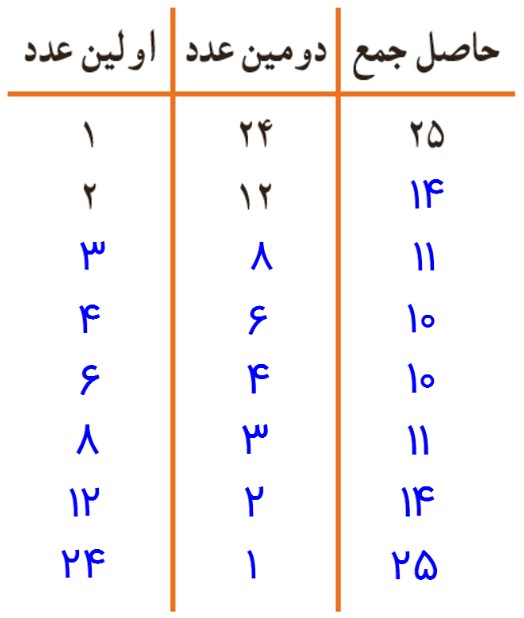
دو عدد 4 و 6 که حاصل ضرب آن ها عدد 24 می شود، دارای کمترین مقدار حاصل جمع یعنی عدد 10 می باشند.
2- با انگشتان یک دست به 5 صورت می توان عدد 1 را نشان داد. به چند صورت می توان عدد 2 را نشان داد؟

برای نشان دادن این عدد به وسیله انگشتان یک دست، به دو انگشت نیاز داریم. با شماره گذاری انگشتان دست کافی است تعداد حالت هایی را که می توان دو شماره غیر تکراری را کنار هم بگذاریم، بشماریم:
\((1\,,\,2)\,,\,(1\,,\,3)\,,\,(1\,,\,4)\,,\,(1\,,\,5)\,\,:\,\,\)4 حالت
3 حالت\((2\,,\,3)\,,\,(2\,,\,4)\,,\,(2\,,\,5)\,\,:\,\,\)
2 حالت\((3\,,\,4)\,,\,(3\,,\,5)\,\,:\,\,\)
1 حالت\((4\,,\,5)\,\,:\,\,\)
توجه کنید که حالت های \((1\,,\,2)\) و \((2\,,\,1)\) یکسان هستند و تکراری اند و به همین دلیل یکی از آنها را می نویسیم. این مورد برای بقیه عددها مانند \((1\,,\,3)\) و \((3,\,1)\) و ... نیز صدق می کند.
با توجه به توضیحات گفته شده حالت های ممکن را با هم جمع می کنیم:
\(4 + 3 + 2 + 1 = 10\)
بنابراین به وسیله انگشتان یک دست به 10 حالت می توان عدد دو را نشان داد.
3- با رقم های 7، 2 و 5 تمام عددهای سه رقمی ممکن را بنویسید (در عددهای شما می تواند رقم های تکراری هم باشد).
\(\begin{array}{l}222\, - \,225\, - \,227\, - \,252\, - \,255\, - \,257\, - \,272\, - \,275\, - \,277\\\\522\, - \,525\, - \,527\, - \,552\, - \,555\, - \,557\, - \,572\, - \,575\, - \,577\\\\722\, - \,725\, - \,727\, - \,752\, - \,755\, - \,757\, - \,772\, - \,775\, - \,777\end{array}\)
4- تعداد زیادی سکهٔ 50 و 100 تومانی داریم. به چند حالت می توان معادل 500 تومان درست کرد؟

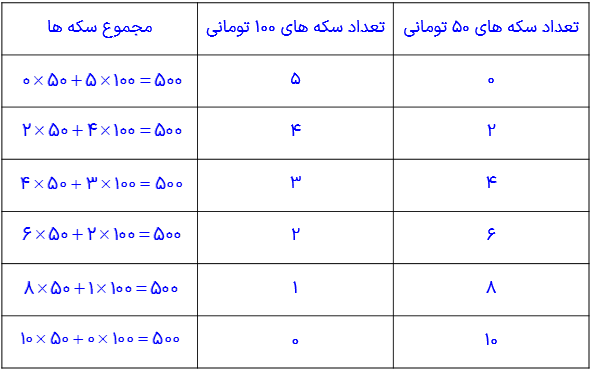
به 6 حالت می توان با سکه های 50 تومانی و 100 تومانی، معادل 500 تومان درست کرد.
گام به گام کتاب های پایه هفتم
گام به گام جامع کتاب ریاضی هفتم
گام به گام جامع کتاب علوم تجربی هفتم
گام به گام جامع کتاب مطالعات اجتماعی هفتم
گام به گام جامع کتاب عربی هفتم
گام به گام جامع کتاب فارسی هفتم
گام به گام جامع کتاب نگارش هفتم
گام به گام جامع کتاب زبان انگلیسی هفتم
گام به گام جامع کتاب کتاب کار انگلیسی هفتم
گام به گام جامع کتاب پیام های آسمانی هفتم
گام به گام جامع کتاب آموزش قرآن هفتم
گام به گام جامع کتاب کار و فناوری هفتم
گام به گام جامع کتاب تفکر و سبک زندگی هفتم
گام به گام جامع کتاب از من تا خدا هفتم
راهبرد حذف حالت های نامطلوب صفحه 4 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد حذف حالت های نامطلوب صفحه 4 درس 1
جواب راهبرد حذف حالت های نامطلوب صفحه 4 درس 1 ریاضی هفتم
در صفحه ۴ درس راهبردهای حل مسئله ریاضی هفتم، شما با راهبرد حذف حالت های نامطلوب روبرو میشوید که برای حل مسائل ریاضی ضروری است. در این صفحه، ما به شما کمک میکنیم تا گام به گام راهبرد حذف حالت های نامطلوب را فرا بگیرید و پاسخ صحیح را پیدا کنید.
یادگیری درس ریاضی هفتم فواید بسیاری دارد، از جمله:
- افزایش توانایی حل مسئله
- ارتقای مهارت های ریاضی
- گسترش دیدگاه و درک ریاضی
برای شروع، ابتدا باید راهبرد حذف حالت های نامطلوب را درک کنید و سپس به صفحه ۴ درس راهبردهای حل مسئله ریاضی هفتم بپردازید. در این مرحله، شما باید گام به گام پیش بروید و هر مرحله را به دقت انجام دهید. با انجام هر مرحله، شما به تدریج در حل مسائل ریاضی پیشرفت میکنید و راهبرد حذف حالت های نامطلوب را بهتر میفهمید.
در پایان، با پاسخ راهبرد حذف حالت های نامطلوب صفحه ۴ درس راهبردهای حل مسئله ریاضی هفتم، شما آماده خواهید شد تا به مرحله بعدی در ریاضی هفتم بروید. بنابراین، گام به گام پیش بروید و با راهبرد حذف حالت های نامطلوب صفحه ۴ درس راهبردهای حل مسئله، ریاضی هفتم را به خوبی فرا بگیرید.
1- مجموع سن سه نفر 14 سال و حاصل ضرب سن آنها 70 است. سن بزرگ ترین نفر چقدر است؟
ابتدا با راهبرد الگوسازی، همهٔ حالت هایی را که ضرب سه عدد طبیعی برابر 70 می شود، بنویسید.
\(\begin{array}{l}1 \times 1 \times 70 = 70\\\\1 \times 2 \times 35 = 70\\\\1 \times 5 \times 14 = 70\\\\1 \times 7 \times 10 = 18\\\\2 \times 5 \times 7 = 70\end{array}\)
به این جدول چه ستونی باید اضافه کنید تا حالت های نامطلوب، حذف شود و فقط حالت مطلوب باقی بماند؟
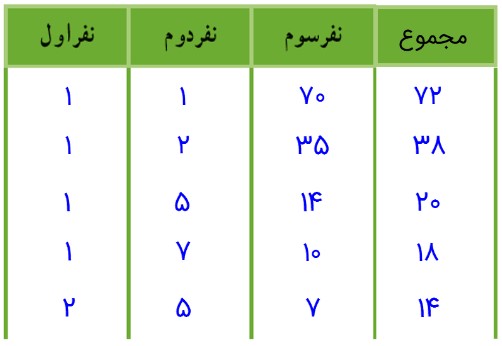
حاصل ضرب سه ستون در همه موارد برابر با 70 است؛ به همین دلیل از نوشتن ستون ضرب صرف نظر شده است و با توجه به جدول می توان متوجه شد که سن بزرگترین فرد 7 سال است.
2- دوست شما یک عدد حسابی کوچک تر از 100 را در نظر گرفته است. شما باید با طرح چند سؤال، عدد مورد نظر را پیدا کنید. او فقط می تواند به سؤال های شما «بله» و «خیر» بگوید. چگونه می توان عدد مورد نظر را پیدا کرد؟
در واقع از 0 تا 99، 100 عدد وجود دارد که فقط یکی مطلوب و مورد نظر است و باقی عددها نامطلوبند. با این توضیح کدام یک از سؤال های زیر مناسب تر است؟ چرا؟
- آیا عدد مورد نظر شما 27 است؟
- آیا عدد مورد نظر شما زوج است؟
- آیا عدد مورد نظر شما یک رقمی است؟
- آیا عدد مورد نظر شما از 50 بزرگ تر است؟
بررسی جواب های سوال ها:
- «آیا عدد مورد نظر شما 27 است؟»:
اگر جواب خیر باشد، تنها عدد 27 از مجموعه اعداد ما حذف می شود.
- «آیا عدد مورد نظر شما زوج است؟»:
اگر پاسخ خیر باشد، 50 عدد زوج از مجموعه اعداد حذف می شوند و 50 تا عدد فرد باقی می ماند.
- «آیا عدد مورد نظر شما یک رقمی است؟»:
اگر پاسخ خیر باشد تنها 10 عدد از مجموعه اعداد حذف می شوند.
- «آیا عدد مورد نظر شما از 50 بزرگ تر است؟»:
اگر پاسخ خیر باشد اعداد 51 تا 99 حذف می شوند.
پس بهترین سوال، سوال «آیا عدد مورد نظر شما از 50 بزرگ تر است؟» می باشد.
با توجه به پاسخ هایی که به سؤال های بالا دادید، یک روش طرح سؤال همراه با نظم و ترتیب بیان کنید که بتوان با پرسیدن آن، به عدد مورد نظر رسید.
در این روش ما عدد 29 را در نظر گرفته ایم:
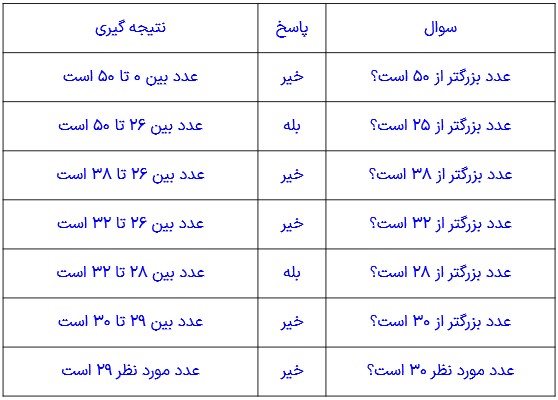
در هر پرسش تقریبا نصف حالت های نامطلوب را حذف می کنیم.
راهبرد الگو یابی صفحه 5 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد الگو یابی صفحه 5 درس 1
جواب راهبرد الگو یابی صفحه 5 درس 1 ریاضی هفتم
1- سه عدد بعدی الگوهای زیر را بنویسید.رابطهٔ بین عددها را توضیح دهید.
\(1\,\,,\,\,4\,,\,\,7\,,\,\,10\,,\,\,13\,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \)
....عددها سه تا سه تا اضافه می شوند. ......
\(\begin{array}{l}1\,\,,\,\,4\,,\,\,7\,,\,\,10\,,\,\,13\,,\,\,16\,,\,\,19\,,\,\,22\\\\1 + 3 = 4\\\\4 + 3 = 7\\\\7 + 3 = 10\\\\10 + 3 = 13\\\\13 + 3 = 16\\\\16 + 3 = 19\\\\19 + 3 = 22\end{array}\)
\(1\,\,,\,\,4\,,\,\,9\,,\,\,16\,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \)
.............................................................
\(\begin{array}{l}1\,\,,\,\,4\,,\,\,9\,,\,\,16\,,\,\,25\,,\,\,36\,,\,\,49\\\\1 \times 1 = 1\\\\2 \times 2 = 4\\\\3 \times 3 = 9\\\\4 \times 4 = 16\\\\5 \times 5 = 15\\\\6 \times 6 = 36\\\\7 \times 7 = 49\end{array}\)
هر عدد از ضرب یک عدد طبیعی در خودش به دست می آید.
\(64\,\,,\,\,32\,\,,\,\,16\,\,,\,\,8\,\,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \,,\,\, \ldots \ldots \)
.............................................................
\(\begin{array}{l}64\,\,,\,\,32\,\,,\,\,16\,\,,\,\,8\,\,,\,\,4\,,\,\,2\,,\,\,1\\\\64 \div 2 = 32\\\\32 \div 2 = 16\\\\16 \div 2 = 8\\\\8 \div 2 = 4\\\\4 \div 2 = 2\\\\2 \div 2 = 1\end{array}\)
هر عدد نصف عدد قبلی است. در واقع هر عدد از تقسیم عدد قبلی بر 2 به دست می آید.
2- شکل دهم با چند چوب کبریت ساخته می شود؟ چرا؟
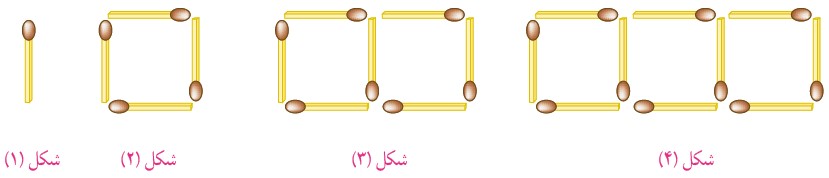
با دقت در شکل ها متوجه می شویم هر شکل با اضافه کردن 3 واحد به شکل قبلی به دست می آید که الگوی آن این چنین است که شکل دهم با 28 کبریت ساخته خواهد شد:
\(1\,\,,\,\,4\,,\,\,7\,,\,\,10\,,\,\,13\,,\,\,16\,,\,\,19\,,\,\,22\,,\,\,25\,,\,\,28\)
3- اگر شکل ها به همین ترتیب ادامه پیدا کند، چه کسری از شکل شمارهٔ 6، رنگی خواهد بود؟
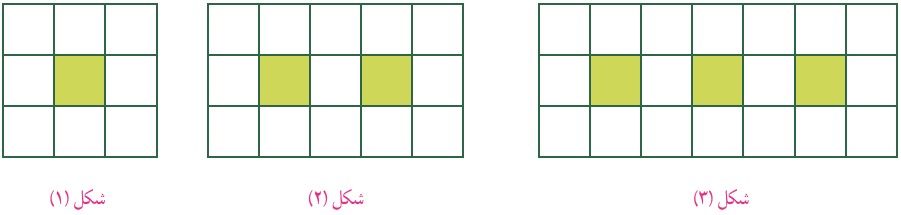
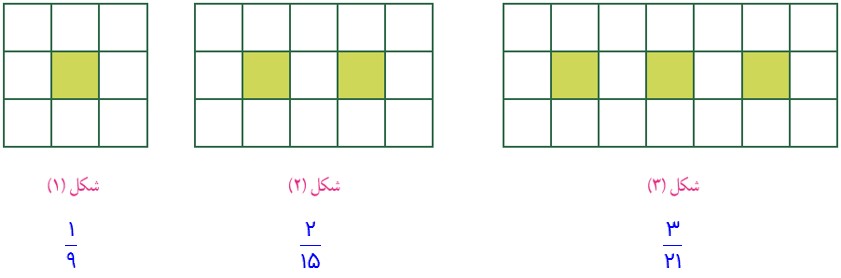
با توجه به کسرها الگوی زیر به دست خواهد آمد:
\(\begin{array}{l}\frac{1}{9}\;\;\;,\;\;\;\frac{2}{{15}}\;\;\;,\;\;\;\frac{3}{{21}}\\\\\frac{1}{9} = \frac{1}{{3 \times 3}}\\\\\frac{2}{{15}} = \frac{2}{{3 \times 5}}\\\\\frac{3}{{21}} = \frac{3}{{3 \times 7}}\end{array}\)
چنانچه الگوی به دست آمده را تا شکل ششم ادامه دهیم به صورت زیر خواهد شد:
\(\begin{array}{l}\frac{1}{{3 \times 3}}\;\;\;,\;\;\;\frac{2}{{3 \times 5}}\;\;\;,\;\;\;\frac{3}{{3 \times 7}}\;\;\;,\;\;\;\frac{4}{{3 \times 9}}\;\;\;,\;\;\;\frac{5}{{3 \times 11}}\\\\\;\;\;,\;\;\;\frac{6}{{3 \times 13}}\;\;\; \Rightarrow \;\;\frac{6}{{39}}\;\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
راهبرد حدس و ازمایش صفحه 6 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد حدس و ازمایش صفحه 6 درس 1
جواب راهبرد حدس و ازمایش صفحه 6 درس 1 ریاضی هفتم
1- 20 دستگاه دوچرخه و سه چرخه در یک پارکینگ (توقفگاه) وجود دارد. اگر تعداد کل چرخ های آنها 45 عدد باشد، چند دوچرخه و چند سه چرخه در توقفگاه وجود دارد؟
درحدس اول تعداد دوچرخه ها را 10 و تعداد سه چرخه ها را هم 10 عدد درنظر بگیرید.
با کامل کردن ردیف اول جدول، حدس خود را بررسی و آزمایش کنید.
با توجه به نتیجهٔ بررسی، باید تعداد سه چرخه ها را بیشتر کرد یا دوچرخه ها را؟ چرا؟
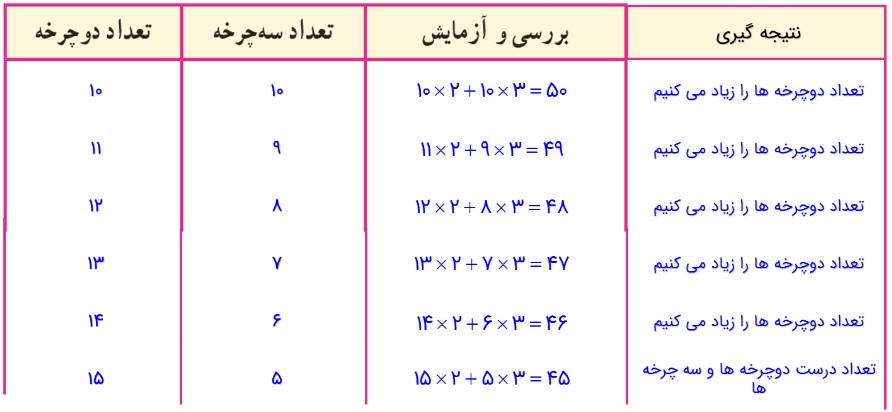
چون عدد 50 از عدد 45 بزرگتر است باید سعی کنیم که از تعداد چرخ ها کاسته شود. باید به تعداد دوچرخه ها افزوده شود و از تعداد سه چرخه ها بکاهیم تا بتوانیم به عدد 45 برسیم.
2- دو زاویه، متمم اند. یکی از این زاویه ها 3 برابر زاویهٔ دیگر است. اندازهٔ هر زاویه را پیدا کنید.
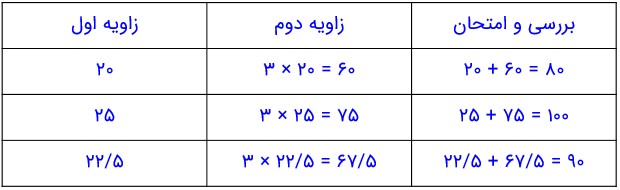
3- به جای مربع چه عددی می توان قرار داد؟
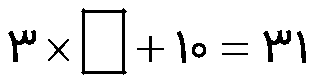
به جای مربع عددهای مختلفی را حدس بزنید. از عدد 10 شروع کنید.
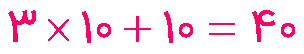
حدس بعدی شما بیشتر از 10 است یا کمتر از آن؟

گام به گام کتاب های پایه هفتم
گام به گام جامع کتاب ریاضی هفتم
گام به گام جامع کتاب علوم تجربی هفتم
گام به گام جامع کتاب مطالعات اجتماعی هفتم
گام به گام جامع کتاب عربی هفتم
گام به گام جامع کتاب فارسی هفتم
گام به گام جامع کتاب نگارش هفتم
گام به گام جامع کتاب زبان انگلیسی هفتم
گام به گام جامع کتاب کتاب کار انگلیسی هفتم
گام به گام جامع کتاب پیام های آسمانی هفتم
گام به گام جامع کتاب آموزش قرآن هفتم
گام به گام جامع کتاب کار و فناوری هفتم
گام به گام جامع کتاب تفکر و سبک زندگی هفتم
گام به گام جامع کتاب از من تا خدا هفتم
راهبرد زیر مسئله صفحه 7 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد زیر مسئله صفحه 7 درس 1
جواب راهبرد زیر مسئله صفحه 7 درس 1 ریاضی هفتم
1- پس انداز هفتگی محمد، 30000 تومان است. او حساب کرده ٥ هفته پس انداز او، نصف قیمت کیفی است که دوست دارد بخرد. قیمت کیف چقدر است؟
الف) پس انداز ٥ هفته چقدر می شود؟
تومان 150000 = 30000 × 5
ب) اگر این عدد نصف قیمت کیف باشد، قیمت کیف چقدر است؟
تومان 300000 = 2 × 150000
2- در یک مجتمع مسکونی استخری به طول، عرض و عمق به ترتیب ١٢، 6 و 1/5 متر وجود دارد. مدیر ساختمان پیشنهاد کرده است که دیوارها و کف استخر ترمیم و بازسازی و سپس رنگ شود. او از یک نقاش خواست تا برآورد کند که انجام این کار چقدر هزینه دارد و به مدیر ساختمان اعلام کند. نقاش ها به طور معمول براساس هر مترمربع برای خودشان دستمزد درنظر می گیرند و قیمت رنگ را هم جداگانه حساب می کنند.
اگر قیمت هر کیلوگرم رنگ ٣٠٠٠٠٠ تومان و دستمزد رنگ کردن هر مترمربع ٢٠٠٠٠ تومان باشد و برای رنگ کردن هر مترمربع استخر 0/3 کیلوگرم رنگ مصرف شود، هزینه این کار را حساب کنید.
الف) مساحت کف استخر را محاسبه می کنیم:
عرض × طول = مساحت
متر مربع 72 = 6 × 12
ب) مساحت دیواره های استخر را محاسبه می کنیم. توجه داشته باشید که دیواره های رو به رو با هم مساوی هستند؛ بنابراین یکی از دیواره ها را محاسبه کرده و سپس نتیجه را دو برابر می کنیم:
\( = \,12 \times 1/5 = 18 \Rightarrow 18 \times 2 = 36\) عمق × طول
\( = \,6 \times 1/5 = 9 \Rightarrow 9 \times 2 = 18\) عمق × عرض
پ) حال مساحت کف دیواره ها را با هم جمع می کنیم:
متر مربع 126 = 18 + 36 + 72
ت) مقدار رنگ مورد نیاز را محاسبه می کنیم:

ث) هزینه رنگ را مورد نیاز را محاسبه می کنیم:
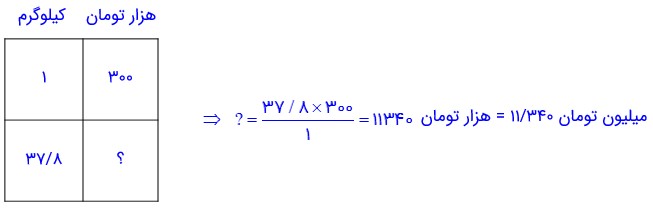
ج) دستمزد نقاش را هم محاسبه می کنیم:
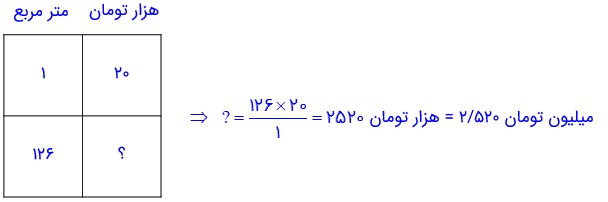
چ) هزینه کار را در نهایت محاسبه می کنیم:
\(11/340 + 2/520 = 13/860\)میلیون تومان
3- میوه فروشی، پرتقال ها را کیلویی ١٧٥٠٠ تومان می فروخت. از او سؤال کردم چگونه قیمت این پرتقال ها را تعیین کرده است؟
او پاسخ داد: من از میدان میوه و تره بار ٨٠ کیلوگرم پرتقال خریدم کیلویی ١٢٠٠٠ تومان. حدود 10% پرتقال ها در حمل و نقل و پس از چند روز ماندن در مغازه خراب می شود و از بین می رود. حدود ١٠٠٠٠٠ تومان کرایه حمل و نقل از میدان تا مغازه را داده ام.
همچنین تجربه نشان می دهد که حدود ٤٠٠٠٠ تومان از این معامله را باید بابت هزینه های جانبی مثل کرایهٔ مغازه، آب، برق و … کنار بگذارم. در این صورت میزان سود این میوه فروش از این معامله را حساب کنید.
الف) محاسبه ی مقدار پولی که میوه فروش برای خرید پرتقال ها پرداخت کرده است:

ب) مقدار پرتقال های باقی مانده را بعد از حمل و نقل نگهداری نیز محاسبه می کنیم (10% یعنی 0/1):
\(80 \times (1 - 0/1) = 80 \times 0/9 = 72\) کیلوگرم
پ) همه هزینه های پرداختی توسط فروشنده بابت خرید میوه، کرایه حمل و نقل و کرایه مغازه و ... را نیز محاسبه می کنیم:
\(960 + 100 + 40 = 1100\) تومان 1100000 = هزار تومان
ت) میزان درآمد از پرتقال های باقی مانده را نیز محاسبه می کنیم:
\(72 \times 17500 = 1260000\) تومان
ث) حال میزان سود این میوه فروش را محاسبه می کنیم:
\(1260000 - 1100000 = 160000\) تومان
این میوه فروش از فروش پرتغال ها، 160000 تومان سود می برد.
راهبرد حل مسئله ساده تر صفحه 8 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد حل مسئله ساده تر صفحه 8 درس 1
جواب راهبرد حل مسئله ساده تر صفحه 8 درس 1 ریاضی هفتم
1-- قطر خورشید 1392530 کیلومتر وقطر کرهٔ زمین 12756/6 کیلومتر است. قطر خورشید تقریباً چند برابر قطر زمین است؟
برای ساده شدن مسئله بهتر است از عددهای ساده تر (برای مثال تقریبی از عدد) استفاده کنید.
\(\begin{array}{l}1392530 \simeq 1000,000\\\\12756/6 \simeq \end{array}\)
\(\begin{array}{l}1392530 \simeq 1000,000\\\\12756/6 \simeq 10,000\end{array}\)
خلاصهٔ مسئله ساده شده را بنویسید و پاسخ دهید.
\(\frac{{1000,000}}{{10,000}} = 100\)
قطر خورشید 100 برابر قطر زمین است.
2- حاصل عبارت مقابل را به دست آورید.
\(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \cdots + \frac{1}{{1024}}\)
به جای حل کردن عبارت بالا، ابتدا ساده شدهٔ این مسئله را حل کنید.
\(\begin{array}{l}\frac{1}{2} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4} = \frac{3}{4}\\\\\frac{1}{2} + \frac{1}{4} + \frac{1}{8} = \frac{4}{8} + \frac{2}{4} + \frac{1}{8} = \frac{7}{8}\\\\\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} = \frac{8}{{16}} + \frac{4}{{16}} + \frac{2}{{16}} + \frac{1}{{16}} = \frac{{15}}{{16}}\end{array}\)
در پاسخ ها چه الگو و رابطه ای تشخیص می دهید که به کمک آن بتوانید پاسخ مسئلهٔ اصلی را بدون محاسبه بنویسید؟
اگر دقت کنیم، متوجه می شویم که در هر مرحله در کسر حاصل، صورت یک واحد کمتر از مخرج است. بنابراین برای کسر نیز می توان این گونه عمل کرد:
\(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \cdots + \frac{1}{{1024}} = \frac{{1023}}{{1024}}\)
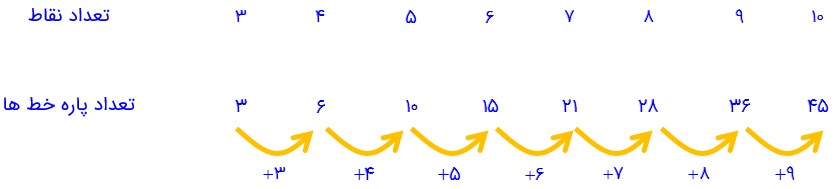
3- اگر 10 نقطه را که هیچ سه تای آنها روی یک خط نیستند، دو به دو به هم وصل کنیم، چند پاره خط به وجود می آید؟
تعداد پاره خط ها در واقع مجموع تعداد ضلع ها و تعداد قطرهاست.
یک الگو بیابید و برای 10 نقطه نتیجه گیری کنید.
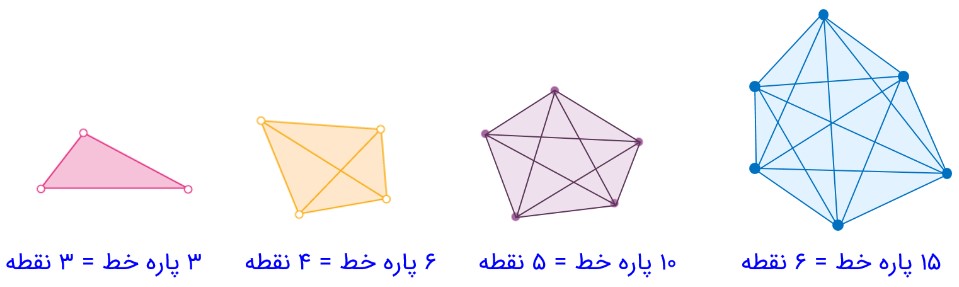
با توجه به تعداد پاره خط های به دست آمده در هر شکل، الگوی زیر به دست می آید:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
راهبرد روش های نمادین صفحه 9 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ راهبرد روش های نمادین صفحه 9 درس 1
جواب راهبرد روش های نمادین صفحه 9 درس 1 ریاضی هفتم
1- احمد 200000 تومان پول داشت. او 4 دفتر خرید و 20000 تومان برایش باقی ماند.قیمت هر دفتر چقدر است؟
متن این سؤال را می توانید با تساوی مقابل نشان دهید.

مربع، نشان دهندهٔ چه چیزی است؟
نشان دهنده قیمت هر دفتر می باشد.
اکنون می توانید عددی را که باید در مربع قرار گیرد، حدس بزنید و آزمایش کنید.
(در فصل سوم، این مسئله را به روش دیگری حل خواهید کرد.)
برای حل این مسئله به جای علامت مربع عددهای مختلفی را قرار می دهیم تا جواب درست را پیدا کنیم:
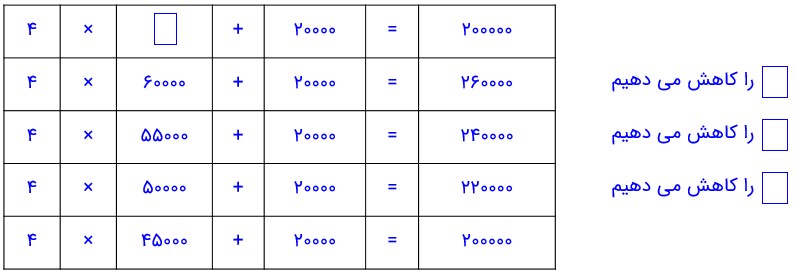
قیمت هر دفتر 45000 تومان می باشد.
2- فاطمه کتاب داستانی را در 6 ساعت مطالعه کرد و 10 صفحه از آن باقی ماند.اگر این کتاب 100 صفحه داشته باشد، فاطمه به طور متوسط در هر ساعت چند صفحه از آن را مطالعه کرده است؟
صورت مسئله به صورت رو به رو خواهد بود. بنابراین با استفاده از شیوه حدس و آزمایش، جواب مسئله را به دست خواهیم آورد:

3- یک سالن مستطیل شکل داریم. می خواهیم در مکانی از سقف این سالن، یک دریچهٔ خنک کن قرار دهیم؛ به طوری که از 4 گوشهٔ آن به یک اندازه فاصله داشته باشد. محل دریچه را تعیین کنید.
با توجه به این که سالن مستطیل شکل و در مستطیل، قطرها با هم برابرند و همدیگر را نصف می کنند، بنابراین بهترین محل برای دریچه خنک کن جایی است که دو قطر همدیگر را قطع می کنند.
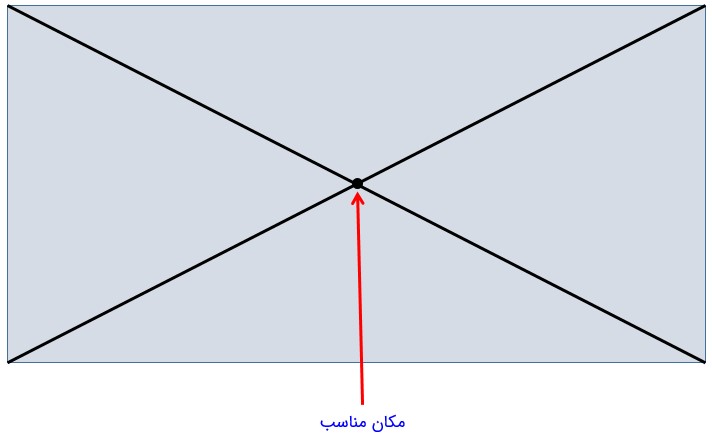
بهترین محل برای نصب دریجه خنک کن در سقف، نقطه مشخص شده در شکل بالا می باشد، زیرا این مکان از 4 گوشه به یک اندازه فاصله دارد.
گام به گام کتاب های پایه هفتم
گام به گام جامع کتاب ریاضی هفتم
گام به گام جامع کتاب علوم تجربی هفتم
گام به گام جامع کتاب مطالعات اجتماعی هفتم
گام به گام جامع کتاب عربی هفتم
گام به گام جامع کتاب فارسی هفتم
گام به گام جامع کتاب نگارش هفتم
گام به گام جامع کتاب زبان انگلیسی هفتم
گام به گام جامع کتاب کتاب کار انگلیسی هفتم
گام به گام جامع کتاب پیام های آسمانی هفتم
گام به گام جامع کتاب آموزش قرآن هفتم
گام به گام جامع کتاب کار و فناوری هفتم
گام به گام جامع کتاب تفکر و سبک زندگی هفتم
گام به گام جامع کتاب از من تا خدا هفتم
مرور راهبرد ها صفحه 10 درس راهبردهای حل مسئله ریاضی هفتم
پاسخ مرور راهبرد ها صفحه 10 درس 1
جواب مرور راهبرد ها صفحه 10 درس 1 ریاضی هفتم
1- \(\frac{1}{3}\) دانش آموزان کلاسی بسکتبال و \(\frac{1}{5}\) دانش آموزان آن کلاس، فوتبال بازی می کنند. سایر دانش آموزان که تعدادشان 14 نفر است، بازی آنها را تماشا می کنند. این کلاس چند دانش آموز دارد؟
ابتدا کسری از کلاس را که در حال ورزش کردن هستند را بدست می آوریم؛ سپس آن را از مقدار 1 کم کرده تا آن کسر از بچه هایی که در حال تماشا کردن بازی ها را هستند بدست می آوریم. از آن جا تعداد دانش آموزان کلاس را بدست می آوریم؛ بنابراین:
\(\frac{1}{3} + \frac{1}{5} = \frac{{5 + 3}}{{15}} = \frac{8}{{15}}\)
\(\frac{8}{{15}}\) بچه ها در حال ورزش کردن هستند.
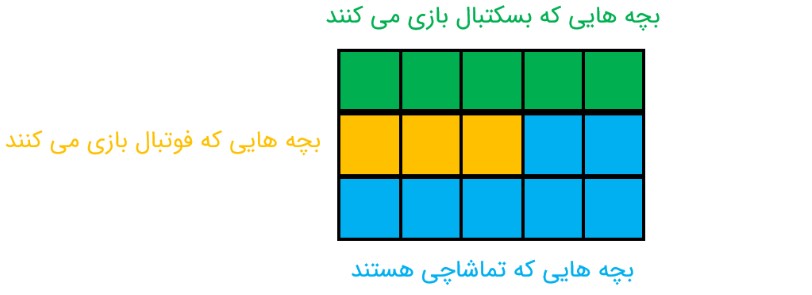
با توجه به رنگ ها مشخص می شود که \(\frac{7}{{15}}\) از بچه ها مشغول تماشای بازی هستند که تعداد آن ها برابر با 14 نفر است؛ پس از آن جهت که هفت خانه مربوط به تماشاچی ها برابر با 14 نفر است، پس مشخص می شود که هر خانه نماینده 2 نفر است؛ بنابراین تعداد دانش آموزان این کلاس 30 نفر می باشند:
30 = 15 × 2
2- مساحت مربعی به ضلع 100 سانتی متر، 1متر مربع است. اگر از ضلع مربع 10 درصد کم کنیم، مساحت مربع چند درصد کم می شود؟
از راهبرد زیر مسئله استفاده می کنیم:
الف) ابتدا 10 درصد 100 سانتی متر را محاسبه می کنیم که برابر 10 سانتی متر می شود:
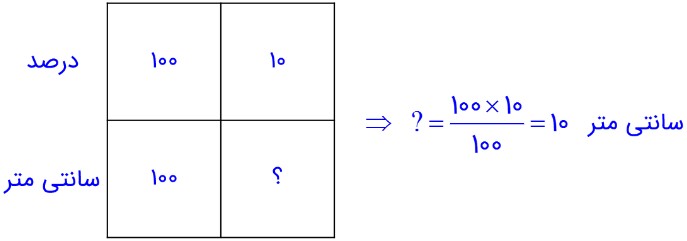
ب) طول ضلع مربع جدید را حساب می کنیم:
سانتی متر 90 = 10 – 100
پ) مساحت هر دو مربع قدیم و جدید را بر اساس سانتی متر محاسبه می کنیم:
سانتی متر مربع 10000 = 100 × 100 مربع قدیم
سانتی متر مربع 8100 = 90 × 90 مربع قدیم
ت) نسبت مساحت مربع جدید به مساحت مربع قدیم را حساب می کنیم:
\(\frac{{8100}}{{10000}} = \frac{{81}}{{100}} = \% 81\)
ث) اختلاف مساحت ها را به صورت درصد می نویسیم:
%100 - %81 = %19
بنابراین مساحت مربع جدید 19% از مربع قدیم کمتر است.
3- کشاورزی زمین خود را به نسبت های زیر بذر پاشی کرده است:
گندم: %45 جو: %37/5 ذرت: % 17/5
اگر مساحت زمین او 15 هکتار باشد، مساحت زیر کشت هر بذر را حساب کنید.
از راهبرد زیر مسئله کمک می گیریم:
الف) مساحت زیر کشت گندم را محاسبه می کنیم:
\(\frac{{45}}{{100}} = \frac{?}{{15}} \Rightarrow ? = \frac{{45 \times 15}}{{100}} = \frac{{675}}{{100}} = 6/75\)
این کشاورز 6/75 هکتار از زمین خود را گندم کاشته است.
ب) مساحت زیر کشت جو را محاسبه می کنیم:
\(\frac{{37/5}}{{100}} = \frac{?}{{15}} \Rightarrow ? = \frac{{37/5 \times 15}}{{100}} \simeq \frac{{562}}{{100}} = 5/62\)
این کشاورز 5/62 هکتار از زمین خود را جو کاشته است.
پ) سپس مساحت زیر کشت دو قسمت گندم و جو را با هم جمع می کنیم:
6/75+5/62=12/37
ت) مساحت کل زمین را از جمع مساحت قسمت های گندم و جو کم می کنیم تا مساحت قسمت زیر کشت ذرت به دست بیاید:
15 – 12/37 = 2/63
این کشاورز تقریبا 2/63 هکتار از زمین خود را ذرت کاشته است.
4- حاصل عبارت رو به رو را پیدا کنید.
\(1\frac{1}{2} \times 1\frac{1}{3} \times 1\frac{1}{4} \times \cdots \times 1\frac{1}{{100}} = \)
از راهبرد حل ساده تر و الگویابی استفاده می کنیم:
\(1\frac{1}{2} \times 1\frac{1}{3} \times 1\frac{1}{4} \times \cdots \times 1\frac{1}{{100}} = \frac{3}{2} \times \frac{4}{3} \times \frac{5}{4} \times \cdots \times \frac{{101}}{{100}} = \frac{{101}}{2}\)
5- در یک کارگاه تولیدی، 4960 جفت کفش تولید شده که \(\frac{3}{8}\) آنها پسرانه و بقیه دخترانه است.اگر قیمت هر جفت کفش پسرانه 350000 تومان و قیمت هر جفت کفش دخترانه 420000 تومان باشد، درآمد این کارگاه چقدر است؟
از راهبرد زیر مسئله استفاده می کنیم:
الف) ابتدا تعداد کفش های پسرانه را به دست می آوریم:
\(\frac{3}{8} \times \frac{{4960}}{1} = \frac{{14880}}{8} = 1860\)جفت
ب) تعداد کفش های دخترانه را به دست می آوریم:
جفت 3100 = 1860 – 4960
پ) درآمد حاصل از فروش کفش های پسرانه و دخترانه را به دست می آوریم:
درآمد فروش کفش های پسرانه:
\(1860 \times 350,000 = 651,000,000\)تومان
درآمد فروش کفش های دخترانه:
\(3100 \times 420,000 = 1,302,000,000\)تومان
درآمد حاصل برابر خواهد بود با:
\(1,302,000,000 + 650,000,000 = 1,952,000,000\)تومان
6- سارا یک بازی روی صفحهٔ شطرنجی انجام می دهد.مهرهٔ او روی خانهٔ \(\left[ \begin{array}{l}2\\3\end{array} \right]\) است. او ابتدا مهره اش را 3 خانه به سمت راست، سپس 4 خانه به سمت بالا و در انتها 2 خانه به سمت چپ می برد.در حال حاضر مهرهٔ سارا روی کدام خانه قرار دارد؟
از راهبرد رسم شکل استفاده می کنیم:
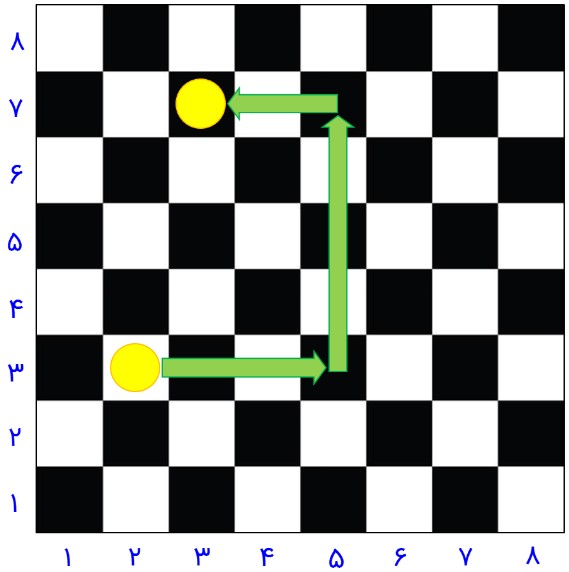
با توجه به پیکان های رسم شده، مشخص است که مهره سارا در حال حاضر بر روی خانه \(\left[ \begin{array}{l}3\\7\end{array} \right]\) قرار دارد.
7- چه کسری از شکل زیر رنگی است؟ توضیح دهید.
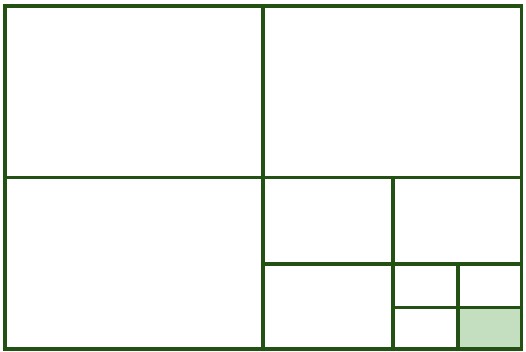
اگر تقسیم شکل را ادامه دهیم، شکل به 64 خانه تقسیم می شود؛ بنابراین \(\frac{1}{{64}}\) شکل رنگی است.
8- اگر دیوارهای یک استخر با طرح زیر، کاشی کاری شده باشد، چه کسری از دیوار، کاشی آبی دارد؟
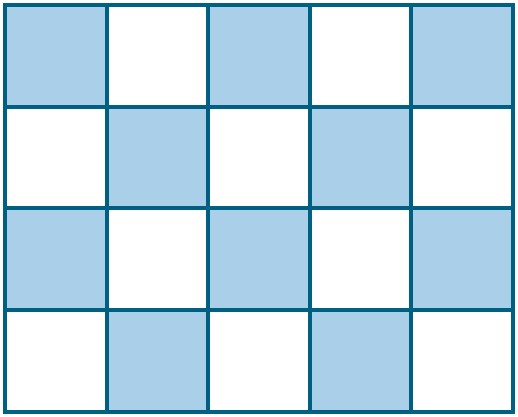
با شمارش کل کاشی ها و نسبت کاشی های آبی به کل کاشی ها، متوجه می شویم که 20 کاشی داریم که 10 تا از آن ها آبی هستند. اگر این نسبت در تمام دیوار رعایت شود، رابطه زیر را خواهیم داشت:
\(\frac{{10}}{{20}} = \frac{1}{2}\)
در نتیجه \(\frac{1}{2}\) دیوار، کاشی آبی دارد.
9- در چند حالت، حاصل ضرب 2 عدد طبیعی، 36 می شود؟ در کدام حالت، حاصل جمع، کمترین مقدار است؟
از راهبرد الگوسازی و حذف حالت های نامطلوب استفاده می کنیم:
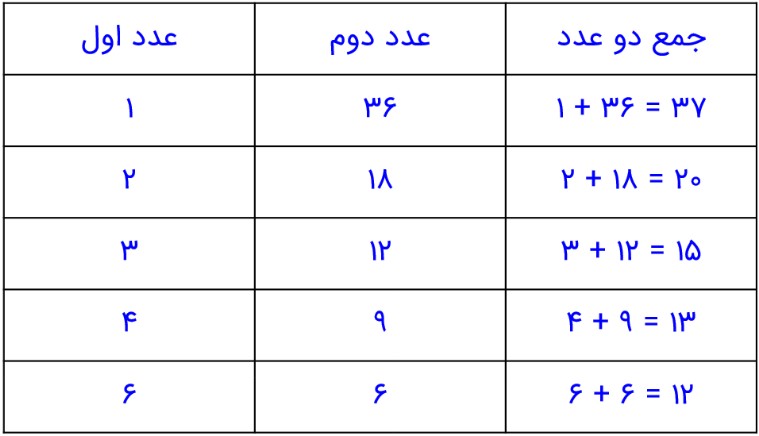
می بینیم که کمترین مجموع، 12 می باشد.
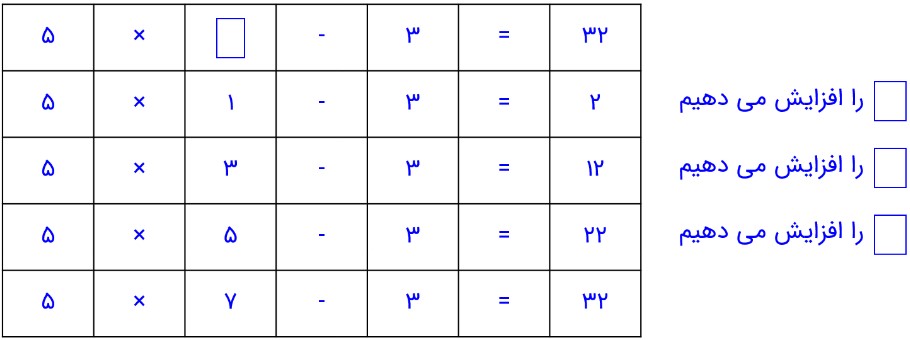
10- عددی را 5 برابر و 3 واحد از آن کم کردیم؛ حاصل، 32 شد. عدد موردنظر چند است؟
از راهبرد حدس و آزمایش استفاده می کنیم:



1736019749.png)















