جواب مثال صفحه 132 درس 6 ریاضی یازدهم تجربی (حد و پیوستگی)
تعداد بازدید : 78.84Mپاسخ مثال صفحه 132 ریاضی یازدهم تجربی
-گام به گام مثال صفحه 132 درس حد و پیوستگی
-مثال صفحه 132 درس 6
-شما در حال مشاهده جواب مثال صفحه 132 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}}\) را محاسبه کنید.
داریم: \(\mathop {\lim }\limits_{x \to 2} (x - 2) = \mathop {\lim }\limits_{x \to 2} ({x^2} - 4) = 0\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x + 2)(x - 2)}}{{x - 2}} = \\\\\mathop {\lim }\limits_{x \to 2} (x + 2) = 4\end{array}\)
توجه داریم که وقتی x به ٢ نزدیک می شود، \(x \ne 2\) پس \(x - 2 \ne 0\) و صورت و مخرج کسر را می توانیم بر x-2 تقسیم کنیم. در نمودارهای زیر توابع \(f(x) = \frac{{{x^2} - 4}}{{x - 2}}\) و g(x)=x+2 رسم و حد آنها در x=2 نمایش داده شده است.
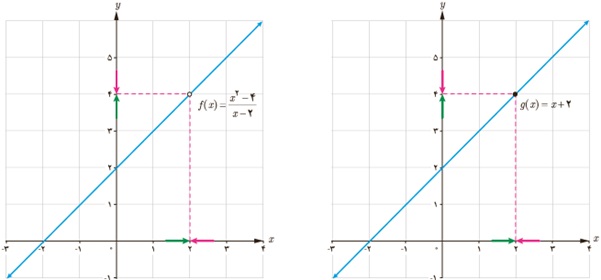
دو تابع g و f برابر نیستند (چرا؟)؛ ولی حد آن ها در x=2 برابر است.
تابع g(x) در آن نقطه x=2 تعریف شده است، اما تابع f(x) تعریف نشده است. بنابراین این دو تابع با هم برابر نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















