جواب کاردرکلاس صفحه 6 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 84.82Mپاسخ کاردرکلاس صفحه 6 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 6 درس هندسۀ تحلیلی و جبر
-کاردرکلاس صفحه 6 درس 1
-شما در حال مشاهده جواب کاردرکلاس صفحه 6 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 نقاط A(2,0) ، B(5,4) و C(-2,3) را در نظر بگیرید و آنها را روی دستگاه مختصات مشخص کنید.
الف محیط مثلث ABC را با محاسبهٔ طول اضلاع آن به دست آورید.
\(\begin{array}{l}AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \sqrt {{{\left( {2 - 5} \right)}^2} + {{\left( {0 - 4} \right)}^2}} = \sqrt {9 + 16} = 5\\\\AC = \;.....\\\\BC = \;....\\\\P = \;.....\end{array}\)
ب ABC چه نوع مثلثی است؟
پ به دو روش نشان دهید ABC یک مثلث قائم الزاویه است. سپس مساحت آن را حساب کنید.
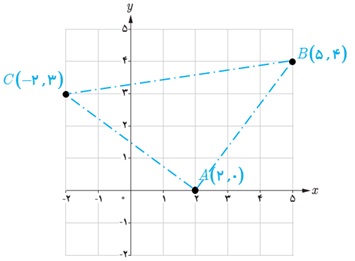
الف
\(\begin{array}{l}AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \sqrt {{{\left( {2 - 5} \right)}^2} + {{\left( {0 - 4} \right)}^2}} = \sqrt {9 + 16} = 5\\\\AC = \;\sqrt {{{\left( {{x_A} - {x_C}} \right)}^2} + {{\left( {{y_A} - {y_C}} \right)}^2}} = \sqrt {{{\left( {2 - \left( { - 2} \right)} \right)}^2} + {{\left( {0 - 3} \right)}^2}} = \sqrt {16 + 9} = 5\\\\BC = \;\sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} = \sqrt {{{\left( {5 - \left( { - 2} \right)} \right)}^2} + {{\left( {4 - 3} \right)}^2}} = \sqrt {49 + 1} = \sqrt {50} = 5\sqrt 2 \\\\P = \;AB + AC + BC = 5 + 5 + 5\sqrt 2 = 10 + 5\sqrt 2 = 5\left( {2 + \sqrt 2 } \right)\end{array}\)
ب مثلث متساوی الساقین است؛ زیرا دو ضلع آن با هم برابر هستند.
پ روش اول رابطه فیثاغورس:
\(B{C^2} = A{B^2} + A{C^2} \Rightarrow {\left( {5\sqrt 2 } \right)^2} = {5^2} + {5^2} \Rightarrow 50 = 25 + 25\)
روش دوم ( ) :
\(\left. \begin{array}{l}{m_{AB}} = \frac{{{y_A} - {y_B}}}{{{x_A} - {x_B}}} = \frac{{0 - 4}}{{2 - 5}} = \frac{4}{3}\\{m_{AC}} = \frac{{{y_A} - {y_C}}}{{{x_A} - {x_C}}} = \frac{{0 - 3}}{{2 - \left( { - 2} \right)}} = - \frac{3}{4}\end{array} \right\} \Rightarrow {m_{AB}} \times {m_{AC}} = - 1 \Rightarrow AB \bot AC \Rightarrow \widehat A = {90^ \circ }\)
مساحت مثلث ABC :
\(S = \frac{1}{2}AB \times AC = \frac{1}{2} \times 5 \times 5 = \frac{{25}}{2}\)
2 در یکی از جاده های کشور، تصادفی رخ داده است که مختصات نقطهٔ تصادف روی نقشهٔ مرکز امداد به صورت P(50,30) است. پایگاه های امداد هوایی که به محل تصادف نزدیک اند، در نقاط A(10,-20) و B(80,90) واقع اند. شما کدام پایگاه را برای اعزام بالگرِد امداد به محل حادثه پیشنهاد می کنید؟ (اعداد برحسب کیلومتر هستند).
ابتدا فاصله هر پایگاه امدادی از محل حادثه را محاسبه می کنیم آنگاه هر کدام که کم تر بود، انتخاب ما خواهد بود :
\(\begin{array}{l}PA = \sqrt {{{\left( {{x_P} - {x_A}} \right)}^2} + {{\left( {{y_P} - {y_A}} \right)}^2}} = \sqrt {{{\left( {50 - 10} \right)}^2} + {{\left( {30 - \left( { - 20} \right)} \right)}^2}} = \sqrt {{{40}^2} + {{50}^2}} = 10\sqrt {41} \simeq 64\\PB = \sqrt {{{\left( {{x_P} - {x_B}} \right)}^2} + {{\left( {{y_P} - {y_B}} \right)}^2}} = \sqrt {{{\left( {50 - 80} \right)}^2} + {{\left( {30 - 90} \right)}^2}} = \sqrt {{{\left( { - 30} \right)}^2} + {{\left( { - 60} \right)}^2}} = 30\sqrt 5 \simeq 67\end{array}\)
پایگاه امدادی A بهترین انتخاب ما خواهد بود .
3
الف فاصلهٔ نقطهٔ N(-6,8) تا مبدأ مختصات را محاسبه کنید.
ب فاصلهٔ نقطهٔ E(xE,yE) تا مبدأ مختصات را به دست آورید.
الف
\(NO = \sqrt {{{\left( {{x_N} - {x_O}} \right)}^2} + {{\left( {{y_N} - {y_O}} \right)}^2}} = \sqrt {{{\left( { - 6 - 0} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = \sqrt {36 + 64} = 10\)
ب
\(EO = \sqrt {{{\left( {{x_E} - {x_O}} \right)}^2} + {{\left( {{y_E} - {y_O}} \right)}^2}} = \sqrt {{{\left( {{x_E} - 0} \right)}^2} + {{\left( {{y_E} - 0} \right)}^2}} = \sqrt {{x_E}^2 + {y_E}^2} \)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















