جواب مرور فصل 6 صفحه 100 درس 6 ریاضی هشتم (مثلث)
تعداد بازدید : 80.7Mپاسخ مرور فصل 6 صفحه 100 ریاضی هشتم
-گام به گام مرور فصل 6 صفحه 100 درس مثلث
-مرور فصل 6 صفحه 100 درس 6
-شما در حال مشاهده جواب مرور فصل 6 صفحه 100 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
مفاهیم و مهارت ها
در این فصل اصطلاحات زیر به کار رفته اند. مطمئن شوید که می توانید با جمله های خود، آنها را توصیف کنید و برای هر کدام مثالی بزنید.
رابطهٔ فیثاغورس:
این رابطه در هر مثلث قائم الزاویه استفاده می شود و در رابطه با سه ضلع مثلث قائم الزاویه می گوید که مربع طول وتر همواره برابر خواهد بود با مجموع مربع های طول دو ضلع دیگر. به عبارتی در مثلث قائم الزاویه زیر داریم:
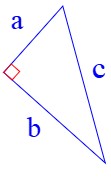
\({c^2} = {a^2} + {b^2}\)
به عنوان مثال در مثلث بالا، اگر داشته باشیم:
\(\left\{ \begin{array}{l}a = 3\\\\b = 4\end{array} \right.\)
آن گاه مقدار وتر با استفاده از رابطه فیثاغورس برابر 5 می شود:
\(\begin{array}{l}{c^2} = {a^2} + {b^2} = {4^2} + {3^2} = 16 + 9 = 25\\\\c = \sqrt {25} = 5\end{array}\)
اجزای متناظر:
در دو شکل هندسی که شبیه هم یا با یکدیگر هم نهشت باشند، آن زاویه هایی که در هر دو شکل با یکدیگر برابر هستند و همچنین آن ضلع هایی که در هر دو شکل به هم مربوط می شوند را اجزای متناظر می گویند؛ مثلاً در شکل های زیر، اجزای متناظر با یکدیگر مشخص شده اند:
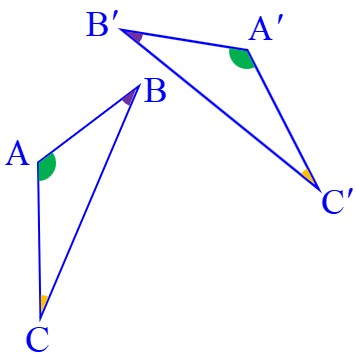
\(\left\{ \begin{array}{l}A \to A'\\\\B \to B'\\\\C \to C'\end{array} \right.\,\,\,\,\,,\,\,\,\,\,\left\{ \begin{array}{l}\widehat A = \widehat {A'}\\\\\widehat B = \widehat {B'}\\\\\widehat C = \widehat {C'}\end{array} \right.\,\,\,\,\,,\,\,\,\,\,\left\{ \begin{array}{l}AB = A'B'\\\\AC = A'C'\\\\BC = B'C'\end{array} \right.\)
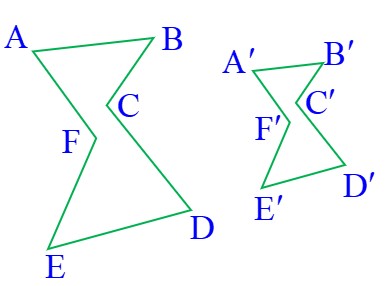
\(\left\{ \begin{array}{l}A \to A'\\\\B \to B'\\\\C \to C'\\\\D \to D'\\\\E \to E'\\\\F \to F'\end{array} \right.\,\,\,\,\,,\,\,\,\,\,\left\{ \begin{array}{l}\widehat A = \widehat {A'}\\\\\widehat B = \widehat {B'}\\\\\widehat C = \widehat {C'}\\\\\widehat D = \widehat {D'}\\\\\widehat E = \widehat {E'}\\\\\widehat F = \widehat {F'}\end{array} \right.\,\,\,\,\,,\,\,\,\,\,\left\{ \begin{array}{l}AB \to A'B'\\\\BC \to B'C'\\\\CD \to C'D'\\\\DE \to D'E'\\\\EF \to E'F'\\\\AF \to A'F'\end{array} \right.\)
هم نهشتیِ مثلث های قائم الزاویه:
دو مثلث قائم الزاویه هم نهشت هستند اگر یکی از موارد زیر در آن ها صدق کند:
1) طول وتر هر دو مثلث و یک زاویه تند از هر دو مثلث با یکدیگر برابر باشند (این حالت، ساده شده ی حالت (ز ض ز) می باشد):
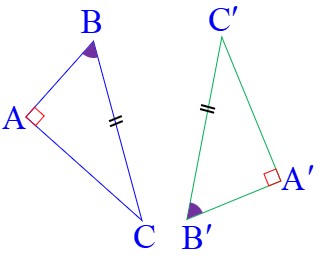
\(\left\{ \begin{array}{l}\widehat B = \widehat {B'}\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک زاویه تند (و ز) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
2) طول وتر هر دو مثلث و یک ضلع قائمه از هر دو مثلث با یکدیگر برابر باشند (این حالت، ساده شده ی حالت (ض ض ض) می باشد):
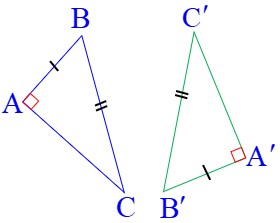
\(\left\{ \begin{array}{l}BC = B'C'\\\\AB = A'B'\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک ضلع قائمه (و ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
حالت های هم نهشتیِ دو مثلث:
دو مثلث وقتی با یکدیگر هم نهشت باشند، یکی از سه حالت زیر پیش می آید:
1- حالت (ض ض ض):
سه ضلع مثلث اول با سه ضلع متناظر آن در مثلث دوم با یکدیگر برابرند:
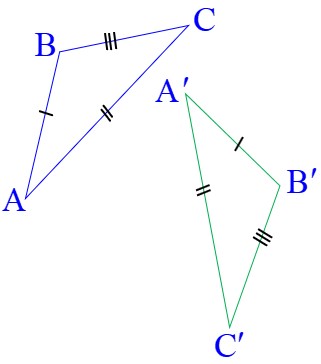
\(\left\{ \begin{array}{l}AB = A'B'\\\\AC = A'C'\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت (ض ض ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
2- حالت (ض ز ض):
دو ضلع و زاویه بین آن ها در مثلث اول با دو ضلع متناظر و زاویه بین آن دو در مثلث دوم با یکدیگر برابرند:
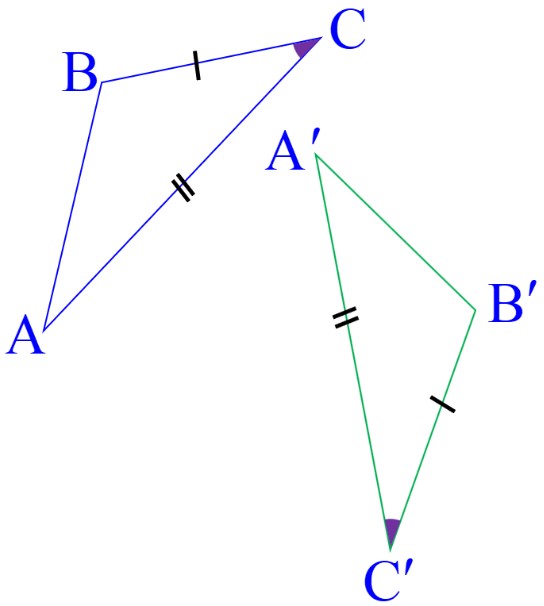
\(\left\{ \begin{array}{l}AC = A'C'\\\\\widehat C = \widehat {C'}\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت (ض ز ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
3- حالت (ز ض ز):
دو زاویه و ضلع بین آن ها در مثلث اول با دو زاویه متناظر و ضلع بین آن دو در مثلث دوم با یکدیگر برابرند:
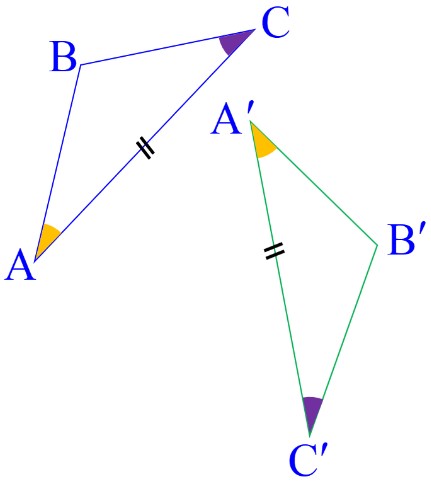
\(\left\{ \begin{array}{l}\widehat A = \widehat {A'}\\\\AC = A'C'\\\\\widehat C = \widehat {C'}\end{array} \right. \Rightarrow \) بنا به حالت (ض ز ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
در این فصل، روش های اصلی زیر مطرح شده اند. هر کدام را با یک مثال توضیح دهید و در دفتر خود خلاصهٔ درس را بنویسید.
پیدا کردن ضلع مجهول مثلث قائم الزاویه:
در یک مثلث قائمالزاویه، با داشتن دو ضلع، میتوان ضلع سوم را با استفاده از رابطهٔ فیثاغورس پیدا کرد.
به عنوان مثال، اگر یک مثلث قائم الزاویه با اضلاع قائمه ی 6 و 8 داشته باشیم، وتر (R) به صورت زیر بدست می آید:
\(\begin{array}{l}{R^2} = {8^2} + {6^2} = 64 + 36 = 100\\\\R = \sqrt {100} = 10\end{array}\)
بررسی قائم الزاویه بودن مثلث با داشتن سه ضلع آن:
اگر سه ضلع یک مثلث داده شده باشد، میتوان با استفاده از رابطهٔ فیثاغورس بررسی کرد که آیا مثلث قائمالزاویه است یا خیر.
به عنوان مثال می خواهیم بررسی کنیم که آیا اضلاعی به طول 7، 8 و 9 تشکیل یک مثلث قائم الزاویه می دهند یا خیر! اول از همه باید بدانیم که کدام ضلع، کدام طول را دارد. می دانیم که در یک مثلث قائم الزاویه، همیشه بیشترین طول برای وتر مثلث می باشد؛ بنابراین اندازه وتر را برابر 9 در نظر می گیریم. در نتیجه 7 و 8 نیز مربوط به اضلاع قائمه می شوند. اکنون این اعداد را در رابطه فیثاغورس می گذاریم:
\(\left. \begin{array}{l}{8^2} + {7^2} = 64 + 49 = 113\\\\{9^2} = 81\end{array} \right\} \Rightarrow {8^2} + {7^2} \ne {9^2}\)
بخاطر وجود نامساوی متوجه می شویم که اضلاع به طول 7، 8 و 9 هیچ گاه تشکیل یک مثلث قائم الزاویه را نخواهند داد. اما اضلاع به طول 5، 12 و 13 تشکیل یک مثلث قائم الزاویه می دهند؛ چرا که در رابطه فیثاغورس صدق می کنند:
\(\left. \begin{array}{l}{5^2} + {12^2} = 25 + 144 = 169\\\\{13^2} = 169\end{array} \right\} \Rightarrow {5^2} + {12^2} = {13^2}\)
نوشتن اجزای متناظر دو شکل هم نهشت:
هنگامی که دو شکل هم نهشت باشند، می توانیم اضلاع و زاویه های متناظر را مشخص کنیم. بعد از مشخص کردن، با نوشتن تساوی بین این اضلاع و زاویه ها، برابر بودن آن ها را نشان می دهیم:
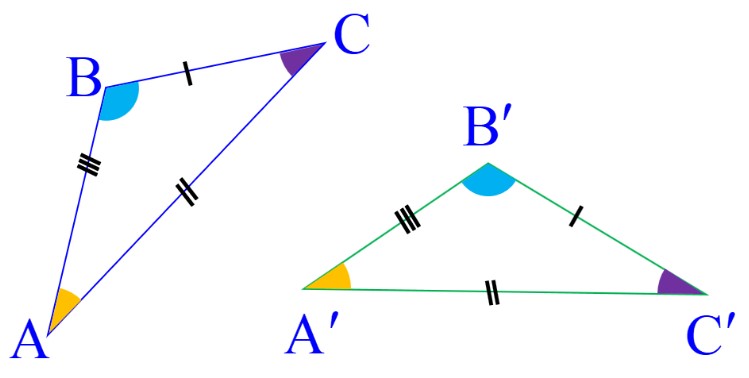
\(\begin{array}{l}A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C' \Rightarrow \left\{ \begin{array}{l}A \to A'\\\\B \to B'\\\\C \to C'\end{array} \right.\\\\ \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'}\\\\\widehat B = \widehat {B'}\\\\\widehat C = \widehat {C'}\end{array} \right.\,\,\,\,\,,\,\,\,\,\,\left\{ \begin{array}{l}AB = A'B'\\\\AC = A'C'\\\\BC = B'C'\end{array} \right.\end{array}\)
هم نهشتی دو مثلث در حالت سه ضلع، دو ضلع و زاویهٔ بین و حالت دو زاویه و ضلع بین:
1- حالت سه ضلع:
سه ضلع مثلث اول با سه ضلع متناظر آن در مثلث دوم با یکدیگر برابرند:

\(\left\{ \begin{array}{l}AB = A'B'\\\\AC = A'C'\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت (ض ض ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
2- حالت دو ضلع و زاویه بین:
دو ضلع و زاویه بین آن ها در مثلث اول با دو ضلع متناظر و زاویه بین آن دو در مثلث دوم با یکدیگر برابرند:

\(\left\{ \begin{array}{l}AC = A'C'\\\\\widehat C = \widehat {C'}\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت (ض ز ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
3- حالت دو زاویه و ضلع بین:
دو زاویه و ضلع بین آن ها در مثلث اول با دو زاویه متناظر و ضلع بین آن دو در مثلث دوم با یکدیگر برابرند:

\(\left\{ \begin{array}{l}\widehat A = \widehat {A'}\\\\AC = A'C'\\\\\widehat C = \widehat {C'}\end{array} \right. \Rightarrow \) بنا به حالت (ض ز ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
هم نهشتی دو مثلث قائم الزاویه در حالت وتر و یک زاویه و حالت وتر و یک ضلع:
1- هم نهشتی دو مثلث قائم الزاویه در حالت وتر و یک زاویه:
طول وتر هر دو مثلث و یک زاویه تند از هر دو مثلث با یکدیگر برابر باشند (این حالت، ساده شده ی حالت (ز ض ز) می باشد):

\(\left\{ \begin{array}{l}\widehat B = \widehat {B'}\\\\BC = B'C'\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک زاویه تند (و ز) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
2- هم نهشتی دو مثلث قائم الزاویه در حالت وتر و یک ضلع:
طول وتر هر دو مثلث و یک ضلع قائمه از هر دو مثلث با یکدیگر برابر باشند (این حالت، ساده شده ی حالت (ض ض ض) می باشد):

\(\left\{ \begin{array}{l}BC = B'C'\\\\AB = A'B'\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک ضلع قائمه (و ض) \( \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\)
حل مسئله های مربوط به هم نهشتی مثلث ها به کمک حالت های بالا:
برای حل مسئلههای هم نهشتی، باید از یکی از شرایط بالا برای اثبات هم نهشتی استفاده کنید.
تمرین های ترکیبی
1 در شکل روبه رو، سطح شیب داری را می بینید طول این سطح شیب دار را به دست آورید.
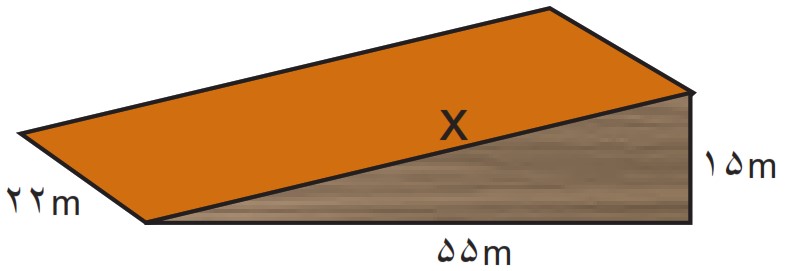
\(\begin{array}{l}{x^2} = {15^2} + {55^2} = 225 + 3025 = 3250\\\\x = \sqrt {3250} = \sqrt {2 \times {5^3} \times 13} = 5\sqrt {130} \end{array}\)
2 الگوی زیر با مثلث های هم نهشت ساخته می شود.

الف دو شکل بعدی را رسم کنید.
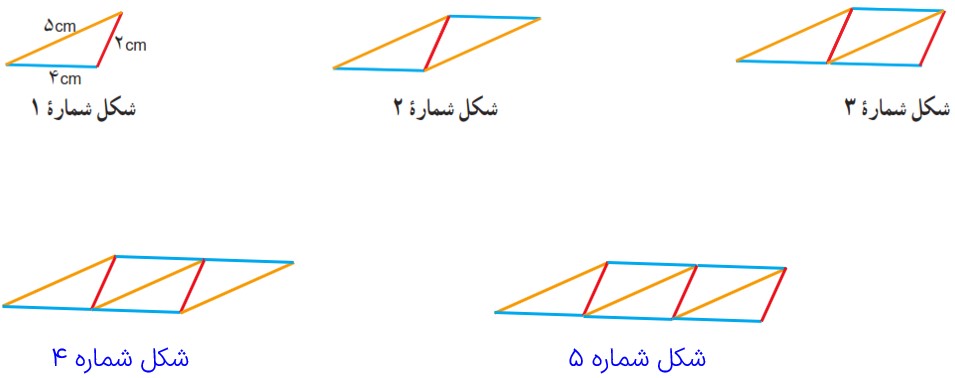
ب محیط هر شکل را پیدا کنید.
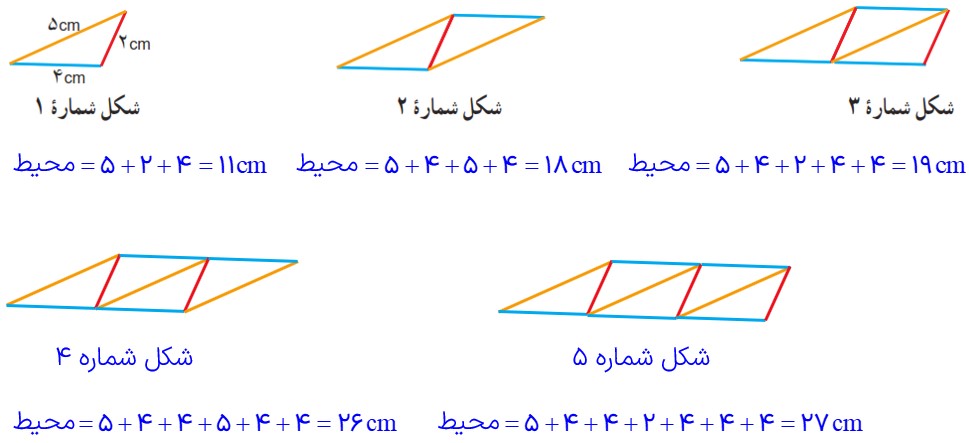
ج محیط شکل شمارهٔ 6 چقدر می شود؟
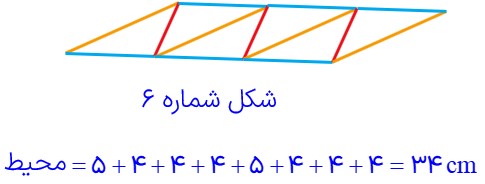
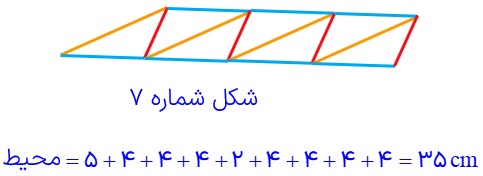
د محیط شکل شمارهٔ 7 چقدر می شود؟
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















