1736019749.png)
گام به گام فعالیت صفحه 98 درس 6 ریاضی هشتم (مثلث)
تعداد بازدید : 62.28Mپاسخ فعالیت صفحه 98 ریاضی هشتم
-گام به گام فعالیت صفحه 98 درس مثلث
-فعالیت صفحه 98 درس 6
-شادی و مهتاب داشتند یک کتاب هندسه را مطالعه می کردند که به این جمله برخوردند:
«هر نقطهٔ روی عمودمُنَصّف یک پاره خط از دو سر آن پاره خط به یک فاصله است.»
1 مهتاب پرسید: «چرا این جمله درست است؟»
شادی سعی کرد مثالی برای درستی آن جمله پیدا کند.
او پاره خطی کشید و عمودمنصّف آن را رسم کرد. نقطه ای را روی آن در نظر گرفت و فاصلهٔ آن نقطه را از دو سر پاره خط اندازه گرفت؛ فاصله ها مساوی بود.
(یادآوری: فاصله دو نقطه از هم برابر طول پاره خطی است که آن نقاط را به هم وصل می کند.)
فکر می کنید شادی توانسته است دلیلی برای درستیِ جملهٔ مورد نظر بیاورد؟
خیر؛ چون فقط یک نقطه را بررسی کرده است.
2 مهتاب گفت: «از کجا بفهمیم این جمله در مورد همهٔ نقاط روی عمودمنصّف درست است؟»
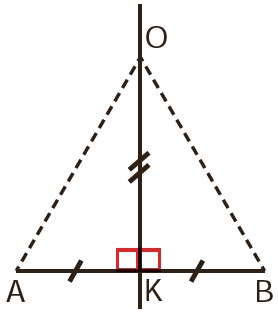
شادی سعی کرد دلیلی برای درستیِ آن جمله پیدا کند. او به شکلی که کشیده بود نگاه کرد. آن را مانند شکل رو به رو علامت گذاری کرد و گفت: «برای همهٔ نقاط روی عمودمنصّف AB، مانند نقطه O، زاویه K زاویه ای قائمه است. (چرا؟)»
به این دلیل که مکان نقطه K همواره روی وسط پاره خط AB قرار دارد. در این نقطه، خط عمودمنصف همواره عمود خواهد بود. به همین دلیل زاویه آن قائمه و مقدار آن 90 درجه خواهد بود.
همچنین AK=KB (چرا؟)
چون OK عمود بر AB است.
OK هم ضلع مشترک دو مثلث است؛ پس \(A\mathop O\limits^\Delta K \cong B\mathop O\limits^\Delta K\) (در چه حالتی؟)
چون OK عمودمنصف AB است؛ بنا به حالت (ض ز ض)
و در نتیجه OA = OB (چرا؟)»
چون دو مثلث هم نهشت هستند.
\(\left\{ \begin{array}{l}AK = BK\\\\A\widehat KO = B\widehat KO = {90^ \circ }\\\\KO = KO\end{array} \right. \Rightarrow A\mathop K\limits^\Delta O = B\mathop K\limits^\Delta O \Rightarrow OA = OB\)
فکر می کنید این بار شادی توانسته است برای درستی جملهٔ مورد نظر دلیلی بیاورد؟
بله.
3 برای درستیِ جملهٔ زیر دلیل بیاورید:
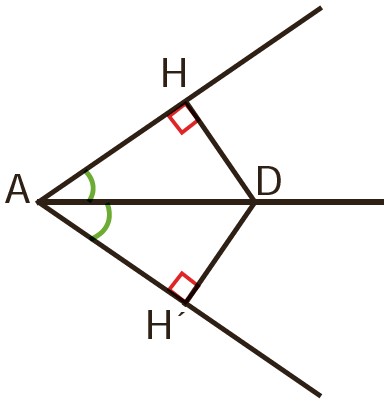
«هر نقطهٔ روی نیمساز یک زاویه از دو ضلع زاویه به یک فاصله است»
(یادآوری: فاصله یک نقطه از یک خط، برابر طول پاره خطی است که از آن نقطه بر آن خط عمود می شود.)
1) AB وتر مشترک هر دو مثلث است.
2) AD نیم ساز است، پس داریم \(\widehat {{A_1}} = \widehat {{A_2}}\)
3) هر دو مثلث، قائم الزاویه هستند.
از 1، 2 و 3 نتیجه می گیریم بنا به حالت وتر و یک زاویه تند (و ز) دو مثلث هم نهشت می باشند.
\(\left\{ \begin{array}{l}AB = AB\\\\\widehat {{A_1}} = \widehat {{A_2}}\\\\\widehat H = \widehat {H'} = {90^ \circ }\end{array} \right. \Rightarrow A\mathop H\limits^\Delta D = A\mathop {H'}\limits^\Delta D \Rightarrow DH = DH'\)
بنابراین هر نقطهٔ روی نیمساز یک زاویه از دو ضلع زاویه به یک فاصله است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
