جواب تمرین صفحه 99 درس 6 ریاضی هشتم (مثلث)

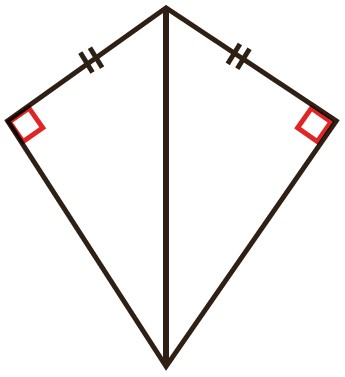
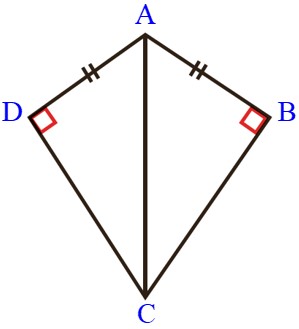
\(\left\{ \begin{array}{l}AB = AD\\\\AC = AC\end{array} \right. \Rightarrow \)بنا به حالت وتر و یک ضلع قائمه (و ض)  \( \Rightarrow A\mathop B\limits^\Delta C \cong A\mathop D\limits^\Delta C\)

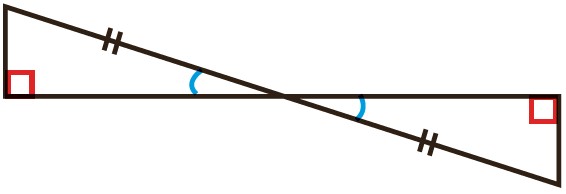
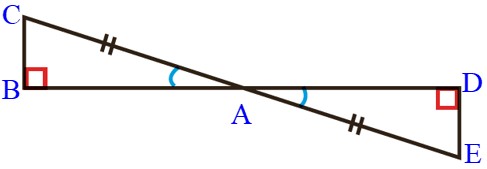
\(\left\{ \begin{array}{l}AC = AE\\\\B\widehat AC = D\widehat AE\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک زاویه تند (و ز) \( \Rightarrow A\mathop B\limits^\Delta C \cong A\mathop D\limits^\Delta E\)

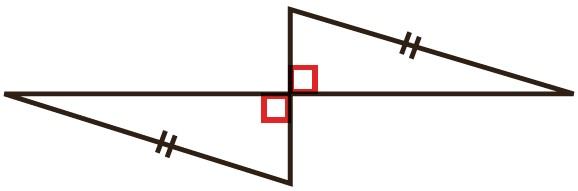
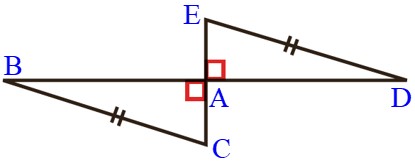
داده های مسئله برای این شکل کافی نیست. حداقل یک تساوی دیگر مورد نیاز است تا بتوانیم هم نهشتی این دو مثلث را اثبات کنیم.

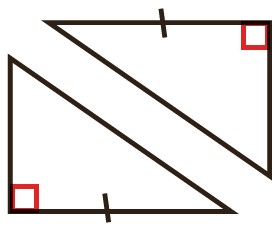
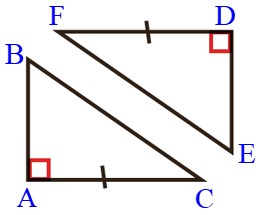
داده های مسئله برای این شکل کافی نیست. حداقل یک تساوی دیگر مورد نیاز است تا بتوانیم هم نهشتی این دو مثلث را اثبات کنیم.

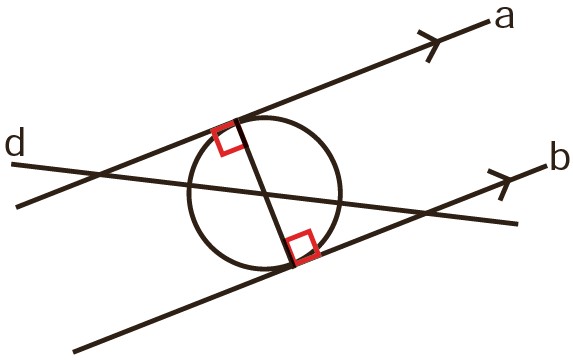
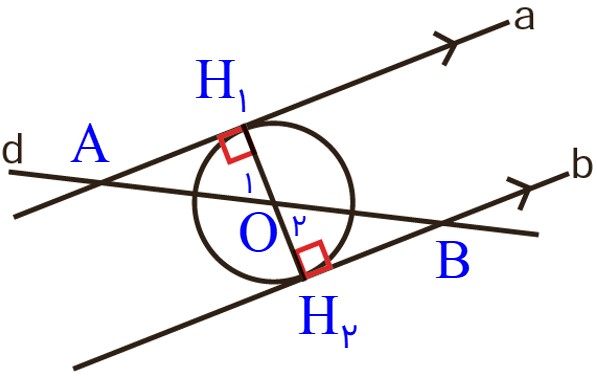
\(\left\{ \begin{array}{l}\widehat {{O_1}} = \widehat {{O_2}}\\\\O{H_1} = O{H_2}\\\\\widehat {{H_1}} = \widehat {{H_2}} = {90^ \circ }\end{array} \right. \Rightarrow \) بنا به حالت (ز ض ز) \( \Rightarrow O\mathop {{H_1}}\limits^\Delta A \cong O\mathop {{H_2}}\limits^\Delta B\)

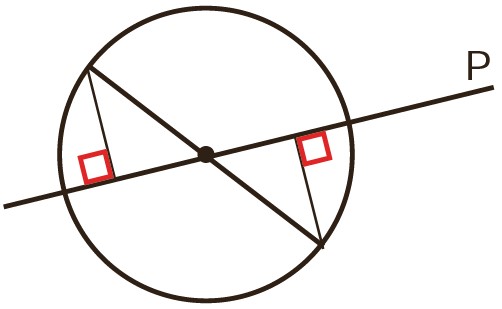
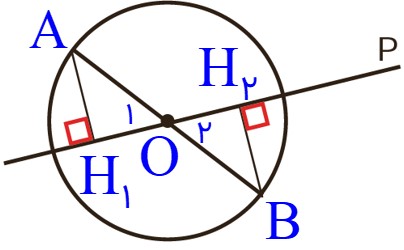
\(\left\{ \begin{array}{l}\widehat {{O_1}} = \widehat {{O_2}}\\\\\widehat {{H_1}} = \widehat {{H_2}} = {90^ \circ }\end{array} \right. \Rightarrow \widehat A = \widehat B\)

\( \Rightarrow \left\{ \begin{array}{l}\widehat {{O_1}} = \widehat {{O_2}}\\\\OA = OB\\\\\widehat A = \widehat B\end{array} \right. \Rightarrow \) بنا به حالت (ز ض ز) \( \Rightarrow O\mathop {{H_1}}\limits^\Delta A \cong O\mathop {{H_2}}\limits^\Delta B\)

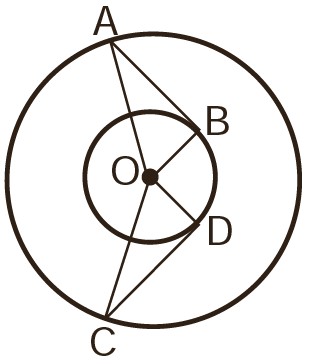
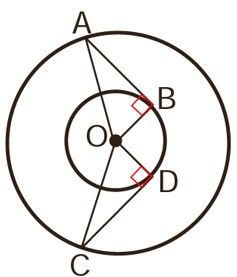
\(\left\{ \begin{array}{l}OA = OC\\\\OB = OD\end{array} \right. \Rightarrow \) بنا به حالت وتر و یک ضلع قائمه (و ض) \( \Rightarrow O\mathop A\limits^\Delta B \cong O\mathop C\limits^\Delta D\)

دوران 180 درجه نسبت به مرکز دایره.

دوران 180 درجه نسبت به مرکز دایره.

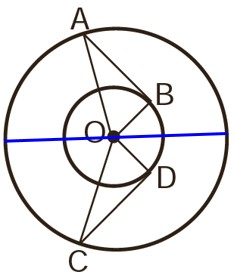
تقارن نسبت به خط آبی رنگ.