گام به گام فعالیت صفحه 90 درس 6 ریاضی هشتم (مثلث)

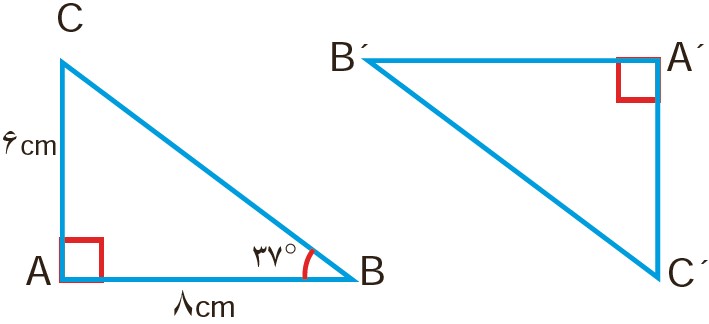
\(\begin{array}{l}B{C^2} = {6^2} + {8^2} = 36 + 64 = 100\\\\BC = \sqrt {100} = 10\,cm\\\\\widehat C = {180^ \circ } - ({90^ \circ } + {37^ \circ }) = {53^ \circ }\end{array}\)

بنابراین اندازه زاویه ها و اضلاع مثلث \(A'B'C'\) بدین صورت خواهد بود:

\(\begin{array}{l}A'B' = 8\,cm\\\\A'C' = 6\,cm\\\\B'C' = 10\,cm\\\\\widehat {A'} = {90^ \circ }\\\\\widehat {B'} = {37^ \circ }\\\\\widehat {C'} = {53^ \circ }\end{array}\)

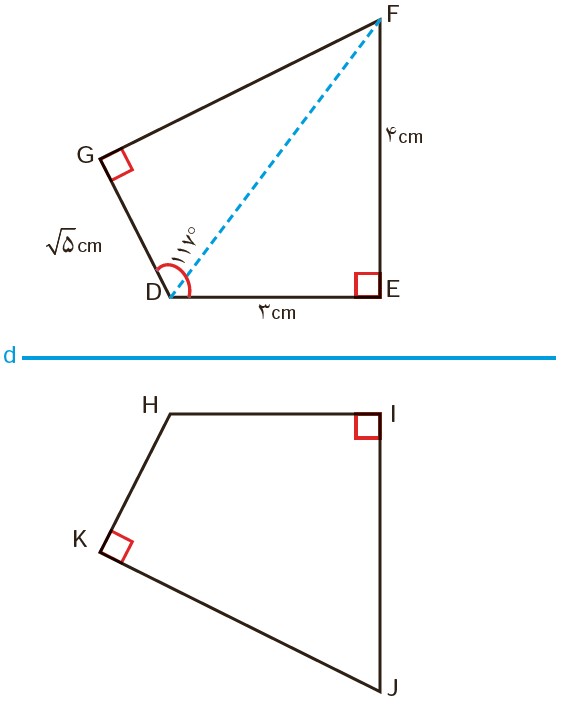
\(\begin{array}{l}\left\{ \begin{array}{l}F{D^2} = F{E^2} + E{D^2}\\\\F{D^2} = {4^2} + {3^2} = 16 + 9 = 25\\\\FD = \sqrt {25} = 5\end{array} \right.\\\\\left\{ \begin{array}{l}F{G^2} = F{D^2} - G{D^2}\\\\F{G^2} = {5^2} - {(\sqrt 5 )^2} = 25 - 5 = 20\\\\FG = \sqrt {20} = 2\sqrt 5 \end{array} \right.\\\\\widehat F = {360^ \circ } - ({9^ \circ } + {90^ \circ } + {117^ \circ }) = {63^ \circ }\end{array}\)

بنابراین اندازه زاویه ها و اضلاع چهار ضلعی HIJK بدین صورت خواهد بود:

\(\begin{array}{l}JI = FE = 4\\\\IK = ED = 3\\\\KH = GD = \sqrt 5 \\\\\widehat H = \widehat D = {117^ \circ }\\\\JH = FD = 5\\\\JK = FG = \sqrt {20} \\\\\widehat J = \widehat F = {63^ \circ }\end{array}\)

از رابطه فیثاغورس برای یافتن اندازه پاره خط های FD و FG استفاده کردیم.

از رابطه مجموع زاویای چهارضلعی برای یافتن اندازه زاویه F استفاده کردیم.

بنا به همنهشتی چهارضلعی ها نیز، اندازه ضلع ها و زاویه های متناظر را در چهار ضلعی HIJK را بدست آوردیم.

مثلث ABC به واسطه بردار \(\overrightarrow {BB'} \) بر روی مثلث \(A'B'C'\) منطبق می شود:

برای دو ضلع AC و A’C’ داریم:

\(\begin{array}{l}AC = A'C'\\\\Y + 3 = 5Y - 5\\\\5Y - Y = 3 + 5\\\\4Y = 8\\\\Y = 2\\\\AC = Y + 3 = 2 + 3 = 5\\\\A'C' = 5Y - 5 = 10 - 5 = 5\end{array}\)

برای دو ضلع BC و B’C’ نیز داریم:

\(\begin{array}{l}BC = B'C'\\\\Z = 7\\\\BC = 7\\\\B'C' = Z = 7\end{array}\)