جواب تمرین صفحه 21 درس 1 ریاضی و آمار دهم انسانی (معادلۀ درجۀ دوم)
تعداد بازدید : 80.71Mپاسخ تمرین صفحه 21 ریاضی و آمار دهم انسانی
-گام به گام تمرین صفحه 21 درس معادلۀ درجۀ دوم
-تمرین صفحه 21 درس 1
-شما در حال مشاهده جواب تمرین صفحه 21 ریاضی و آمار دهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 معادله های زیر را حل کنید.
\(2{x^2} - 8 = 0\) الف
\(2{x^2} - 8 = 0 \Rightarrow 2{x^2} = 8 \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2\)
\((x + 2)(x - 3) = x - 3\) ب
\(\begin{array}{l}(x + 2)(x - 3) = x - 3 \Rightarrow (x + 2)(x - 3) - (x - 3) = 0\\\\ \Rightarrow (x - 3)(x + 2 - 1) = 0 \Rightarrow (x - 3)(x + 1) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}x = - 1\\\\x = 3\end{array} \right.\end{array}\)
\({x^4} - 2{x^2} = 0\) پ
\({x^4} - 2{x^2} = 0 \Rightarrow {x^2}({x^2} - 2) = 0 \Rightarrow \left\{ \begin{array}{l}{x^2} = 0 \Rightarrow x = 0\\\\{x^2} = 2 \Rightarrow x = \pm \sqrt 2 \end{array} \right.\)
\({x^2} = x - \frac{1}{4}\) ت
\(\begin{array}{l}{x^2} = x - \frac{1}{4} \Rightarrow {x^2} - x + \frac{1}{4} = 0 \Rightarrow {(x - \frac{1}{2})^2} = 0\\\\ \Rightarrow x - \frac{1}{2} = 0 \Rightarrow x = \frac{1}{2}\end{array}\)
\(2{x^2} - 8x = 0\) ث
\(2{x^2} - 8x = 0 \Rightarrow 2x(x - 4) = 0 \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x = 4\end{array} \right.\)
\({x^2} - 5x + 6 = 0\) ج
\({x^2} - 5x + 6 = 0 \Rightarrow (x - 2)(x - 3) = 0 \Rightarrow \left\{ \begin{array}{l}x = 2\\\\x = 3\end{array} \right.\)
\(\frac{{{x^2}}}{3} = x\) چ
\(\begin{array}{l}\frac{{{x^2}}}{3} = x \Rightarrow {x^2} = 3x \Rightarrow {x^2} - 3x = 0 \Rightarrow x(x - 3) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x = 3\end{array} \right.\end{array}\)
\({x^2} = 5 - {x^2}\) ح
\(\begin{array}{l}{x^2} = 5 - {x^2} \Rightarrow 2{x^2} = 5 \Rightarrow {x^2} = \frac{5}{2} \Rightarrow x = \pm \sqrt {\frac{5}{2}} \\\\ \Rightarrow x = \pm \frac{{\sqrt {10} }}{2}\end{array}\)
\({x^2} + 4x + 4 = 0\) خ
\({x^2} + 4x + 4 = 0 \Rightarrow {(x + 2)^2} = 0 \Rightarrow x + 2 = 0 \Rightarrow x = - 2\)
\(9{x^2} + 3x - 2 = 0\) د
\(9{x^2} + 3x - 2 = 0 \Rightarrow (3x + 2)(3x - 1) = 0 \Rightarrow \left\{ \begin{array}{l}x = \frac{1}{3}\\\\x = - \frac{2}{3}\end{array} \right.\)
\({(x - 3)^2} = 4\) ذ
\({(x - 3)^2} = 4 \Rightarrow x - 3 = \pm 2 \Rightarrow \left\{ \begin{array}{l}x - 3 = 2 \Rightarrow x = 5\\\\x - 3 = - 2 \Rightarrow x = 1\end{array} \right.\)
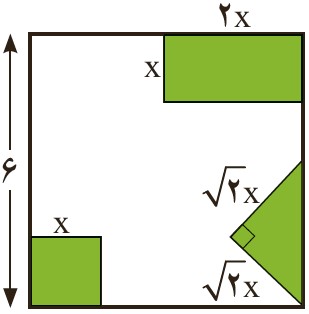
2 از مربعی به ضلع 6cm سه شکل رو به رو بریده شده است. مساحت باقی مانده \(24c{m^2}\) است. طول ضلع کوچک بریده شده چقدر است؟
\( = {6^2} = 36\) مساحت مربع
مساحت بریده شده برابر است با:
\( = {S_1} = {x^2}\) مساحت مربع کوچک
\( = {S_2} = x \times 2x = 2{x^2}\) مساحت مستطیل
\( = {S_3} = \frac{{\sqrt 2 x \times \sqrt 2 x}}{2} = {x^2}\) مساحت مثلث
\({S_1} + {S_2} + {S_3} = {x^2} + 2{x^2} + {x^2} = 4{x^2}\)
\( = 36 - 24 = 12 = 4{x^2}\) مساحت قسمت بریده شده
\( \Rightarrow {x^2} = 3 \Rightarrow x = \pm \sqrt 3 \)
\(x = - \sqrt 3 \) غیر قابل قبول است چون اندازه ضلع منفی نمی شود. بنابراین طول ضلع کوچک بریده شده برابر \(x = \sqrt 3 \) می باشد.
3 معادلهٔ درجه دومی بنویسید که x=2 و x=-3 جواب های آن باشد.
\(\begin{array}{l}\left. \begin{array}{l}x = 2 \Rightarrow x - 2 = 0\\\\x = - 3 \Rightarrow x + 3 = 0\end{array} \right\} \Rightarrow (x - 2)(x + 3) = 0\\\\ \Rightarrow {x^2} + x - 6 = 0\end{array}\)
4 معادلهٔ درجه دومی بنویسید که x=1 ریشهٔ مضاعف آن باشد.
\(x = 1 \Rightarrow x - 1 = 0 \Rightarrow {(x - 1)^2} = 0 \Rightarrow {x^2} - 2x + 1 = 0\)
5 در معادلهٔ \(:{(x - 1)^2} = K\)
الف جواب این معادله را در صورت وجود به ازای K=2، K=4، K=0 و K=-9 به دست آورید.
\(\begin{array}{l}{(x - 1)^2} = K \Rightarrow x - 1 = \pm \sqrt K \Rightarrow x = 1 \pm \sqrt K \\\\K = 2 \Rightarrow x = 1 \pm \sqrt 2 \Rightarrow \left\{ \begin{array}{l}x = 1 + \sqrt 2 \\\\x = 1 - \sqrt 2 \end{array} \right.\\\\K = 4 \Rightarrow x = 1 \pm \sqrt 4 = 1 \pm 2 \Rightarrow \left\{ \begin{array}{l}x = 3\\\\x = - 1\end{array} \right.\\\\K = 0 \Rightarrow x = 1 \pm \sqrt 0 \Rightarrow x = 1\\\\K = - 9 \Rightarrow x = 1 \pm \sqrt { - 9} \end{array}\)
به ازای K=-9 جواب ندارد.
ب به ازای چه مقادیری از K معادله ریشهٔ مضاعف دارد؟
به ازای K=0
پ به ازای چه مقادیری از K معادله دو ریشهٔ حقیقی دارد؟
به ازای K>0 (مقادیر مثبت K)
ت به ازای چه مقادیری از K معادله ریشهٔ حقیقی ندارد؟
به ازای K<0 (مقادیر منفی K)
6 برای ساخت تابلوی راهنمایی «یک طرفه» روی یک پل، مطابق شکل زیر از برچسب های آبی و سفید استفاده می شود. هزینهٔ \(1c{m^2}\) برچسب سفید 30 تومان و هزینهٔ \(1c{m^2}\) برچسب آبی ١٠ تومان است. مجموع هزینهٔ برچسب های سفید و آبی 27/000 تومان شده است.
الف اندازهٔ x چقدر است؟
مساحت مستطیل سفید + مساحت مثلث سفید = مساحت فلش
\( = \frac{1}{2} \times 3x \times 2x + x \times 2x = 5{x^2}\)
هزینه برچسب سفید:
\(5{x^2} \times 30 = 150{x^2}\)
فلش – مستطیل تابلو = مساحت قسمت آبی
\( = 60 \times 40 - 5{x^2} = 2400 - 5{x^2}\)
هزینه برچسب آبی:
\((2400 - 5{x^2}) \times 10 = 24000 - 50{x^2}\)
\( \Rightarrow 150{x^2} + 24000 - 50{x^2} = 27000\) 27000 = مجموع هزینه ها
\(100{x^2} = 3000 \Rightarrow {x^2} = 30 \Rightarrow x = \pm \sqrt {30} \)
\(x = - \sqrt {30} \) غیر قابل قبول است.
ب اگر در این تابلوی راهنمایی، مطابق شکل روبه رو علاوه بر چسب سفید و آبی از خطوط برچسب شبرنگ زرد استفاده کنیم که هزینهٔ 1cm آن 100 تومان است، هزینهٔ رنگ آمیزی تابلو 34/800 تومان می شود. در این حالت اندازهٔ x چقدر است؟

\({a^2} = {(x + \frac{x}{2})^2} + {(2x)^2} = \frac{{25}}{4}{x^2} \Rightarrow a = \pm \frac{5}{2}x \Rightarrow a = \frac{5}{2}x\)
\( = 2a + 3x + 2(2x) = 2(\frac{5}{2}x) + 3x + 4x = 12x\) محیط فلش
\( = 150{x^2} + 24000 - 50{x^2} + 1200x = 34800\) هزینه برچسب زرد
\( = 150{x^2} + 24000 - 50{x^2} + 1200x = 34800\) هزینه رنگ آمیزی تابلو
\(\begin{array}{l} \Rightarrow 10\,0{x^2} + 1200x - 10800 = 0 \Rightarrow {x^2} + 12x - 108 = 0\\\\ \Rightarrow (x + 18)(x - 6) = 0 \Rightarrow x = 6\end{array}\)
جواب x=-18 غیر قابل قبول می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















