جواب تمرین صفحه 29 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 29 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 29 درس هندسه
-تمرین صفحه 29 درس 2
-شما در حال مشاهده جواب تمرین صفحه 29 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1
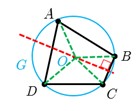
الف دو پاره خط AB و CD مطابق شکل داده شده اند. نقطه ای بیابید که از دو نقطهٔ A و B به یک فاصله باشد و از دو نقطهٔ D و C نیز به یک فاصله باشد.
ب نقطهٔ موردنظر در قسمت (الف) را O می نامیم. اگر نقطۀ O روی عمود منصفِ پاره خط BC باشد و G دایره ای به مرکز O و به شعاع OA باشد، رأس های چهارضلعی ABCD نسبت به دایرهٔ G چه وضعیتی دارند؟ چرا؟

الف
بنابر خاصیت عمود منصف نقطه ای که از دو نقطه A و B به یک فاصله باشد، بر روی عمود منصف پاره خط AB قرار دارد و همچنین نقطه ای که از دو نقطه C و D به یک فاصله باشد، بر روی عمود منصف پاره خط CD قرار دارد. بنابراین جواب مسئله محل برخورد این دو عمود منصف می باشد.

ب
با توجه به بند (الف):
نقطه O روی عمود منصف AB است؛ بنابراین OA=OB (1)
نقطه O روی عمود منصف CD است؛ بنابراین OC=OD(2)
و با توجه به فرض قسمت (ب)، نقطه O روی عمود منصف BC است؛
بنابراین OC=OB (3)
از روابط (1) و (3) نتیجه می گیریم که OA=OC (4)
از روابط (4) و (2) نتیجه می گیریم که OA=OB=OC=OD
بنابراین فاصله نقاط B ، C و D از نقطه O برابر شعاع دایره یعنی OA
است؛ پس این نقاط روی دایره قرار دارند.
2 مثلثی دلخواه رسم کنید و آن را ABC بنامید. عمودمنصف های دو ضلع این مثلث را رسم کنید و نقطهٔ برخورد آنها را O بنامید. به مرکز O و به شعاع OA یک دایره رسم کنید. نقاط B و C نسبت به این دایره چه وضعیتی دارند؟ چرا؟
نقاط B و C روی این دایره اند؛ زیرا :
نقطه O روی عمود منصف BC قرار دارد؛ بنابراین OB=OC (1)
نقطه O روی عمود منصف AB قرار دارد؛ بنابراین OA=OB (2)
از روابط (1) و (2) نتیجه می گیریم که OA=OB=OC ؛ پس نقاط
B و C روی دایره به شعاع OA می باشند.

3 مثلثی دلخواه رسم کنید و آن را ABC بنامید. نیمسازهای دو زاویهٔ این مثلث را رسم کنید و نقطهٔ برخورد آنها را O بنامید. از نقطهٔ O بر سه ضلع مثلث عمود رسم کنید و پای یکی از عمودها را H بنامید. به مرکز O و به شعاع OH دایره ای رسم کنید. اضلاع مثلث ABC نسبت به این دایره چه وضعیتی دارند؟ چرا؟
اضلاع مثلث در پای عمودها بر دایره مماس هستند.
نقطه O روی نیم ساز زاویه A است؛ بنابراین OH=OH” (1)
نقطه O روی نیم ساز زاویه C است؛ بنابراین OH=OH’ (2)
از روابط (1) و (2) نتیجه می گیریم که OH’=OH”
بنابراین OH=OH’=OH” . پس نقاط H’ و H” هم روی این دایره قرار دارند و اگر شعاع در نقطه تماس با خطی، بر آن عمود باشد، پس آن خط بر دایره مماس است، پس اضلاع مثلث بر این دایره مماس هستند.

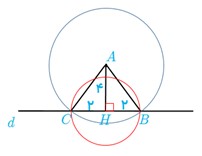
4 فرض کنید نقطهٔ A به فاصلهٔ 4 سانتی متر از خط d باشد. روش رسم هریک از مثلث های زیر را توضیح دهید.
الف مثلثی متساوی الساقین که A یک رأس آن و قاعدهٔ آن بر خط d منطبق باشد.
ب مثلثی که شرایط (الف) را داشته باشد و طول ساق آن 6 سانتی متر باشد.
پ مثلثی رسم کنید که شرایط قسمت (الف) را داشته باشد و مساحت آن 8cm2 باشد.
الف
چون می خواهیم مثلث ABC متساوی الساقین باشد به طوری که AB=AC و ضلع BC روی خط d باشد، پس باید نقاط B و C به فاصله مساوی از A و روی خط d باشند. اگر بخواهیم این نقاط از نقطه A به یک فاصله باشند، باید به مرکز A و شعاع دلخواه دایره رسم کنیم، ولی چون می خواهیم که این نقاط روی خط d هم باشند بنابراین شعاع این دایره باید بزرگتر از 4 سانتی متر باشد، زیرا در غیر این صورت این دایره خط d را در دو نقطه قطع نخواهد کرد.

ب
برای این منظور کافی است دایره ای به شعاع 6 سانتی متر رسم کنیم. این دایره خط d را در نقاط B و C قطع می کند و مثلث ABC جواب مسئله است.

پ
طول ارتفاع 4 سانتی متر است ، پس طول قاعده نظیر را می توان محاسبه کرد:
\(S = \frac{1}{2}AH \times BC \Rightarrow 8 = \frac{1}{2}\left( 4 \right) \times BC \Rightarrow BC = 4\)
می دانیم در هر مثلث متساوی الساقین ارتفاع و میانه بر هم منطبق هستند، بنابراین پای ارتفاع یعنی نقطه H وسط BC قرار دارد. پس به مرکز H و به شعاع نصف اندازه BC ( 2 سانتی متر ) کمان می زنیم تا نقاط B و C به دست آیند. مثلث ABC جواب مسئله می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















