جواب فعالیت صفحه 44 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 80.71Mپاسخ فعالیت صفحه 44 ریاضی یازدهم تجربی
-گام به گام فعالیت صفحه 44 درس هندسه
-فعالیت صفحه 44 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 44 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
فرض کنید مثلث ABC مانند شکل یک مثلث قائم الزاویه و AH ارتفاع وارد بر وتر آن باشد.
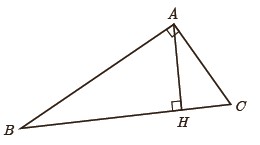
1 نشان دهید دو زاویه از مثلث AHC با دو زاویه از مثلث ABC برابرند و نتیجه بگیرید:
\(A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\)

\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\hat A = {{\hat H}_1} = {90^\circ }\\\end{array}\\{\hat C = \hat C}\end{array}} \right. \Rightarrow A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\)
2 نشان دهید دو زاویهٔ مثلث AHB با دو زاویه از مثلث ABC برابرند و نتیجه بگیرید:
\(A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta B\)

\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\hat A = {{\hat H}_2} = {90^\circ }\\\end{array}\\{\hat B = \hat B}\end{array}} \right. \Rightarrow A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta B\)
3 از (1) و (2) دربارهٔ مثلث های ABC و AHB چه نتیجه ای می گیرید؟
با توجه به کار در کلاس قبلی نتیجه می شود:
\(\left\{ \begin{array}{l}A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\\\\A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta B\end{array} \right. \Rightarrow A\mathop H\limits^\Delta B\sim A\mathop H\limits^\Delta C\)
4
\(\begin{array}{l}A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\;\\\\\; \Rightarrow \;\;\frac{{AH}}{{...}} = \frac{{AC}}{{...}} = \frac{{HC}}{{...}}\;\;\\\\ \Rightarrow \;\;A{C^2} = ....\; \times \;....\end{array}\)
\(\begin{array}{l}A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\;\;\\\\ \Rightarrow \;\;\frac{{AH}}{{AB}} = \frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\;\;\\\\ \Rightarrow \;\;A{C^2} = HC\; \times \;BC\end{array}\)
5
\(\begin{array}{l}A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\;\;\\\\ \Rightarrow \;\;\frac{{AH}}{{...}} = \frac{{AB}}{{...}} = \frac{{HB}}{{...}}\;\;\\\\ \Rightarrow \;\;A{B^2} = ....\; \times \;....\end{array}\)
\(\begin{array}{l}A\mathop B\limits^\Delta C\sim A\mathop H\limits^\Delta C\;\;\\\\ \Rightarrow \;\;\frac{{AH}}{{AC}} = \frac{{AB}}{{BC}} = \frac{{HB}}{{AB}}\;\;\\\\ \Rightarrow \;\;A{B^2} = HB\; \times \;BC\end{array}\)
6
\(\begin{array}{l}A\mathop H\limits^\Delta B\sim A\mathop H\limits^\Delta C\;\;\\\\ \Rightarrow \;\;\frac{{AH}}{{...}} = \frac{{AC}}{{...}} = \frac{{HC}}{{...}}\;\;\\\\ \Rightarrow \;\;A{C^2} = ....\; \times \;....\end{array}\)
\(\begin{array}{l}A\mathop H\limits^\Delta B\sim A\mathop H\limits^\Delta C\;\;\\\\ \Rightarrow \;\;\frac{{AH}}{{HB}} = \frac{{AC}}{{AB}} = \frac{{HC}}{{AH}}\;\;\\\\ \Rightarrow \;\;A{C^2} = HB\; \times \;HC\end{array}\)
7 با جمع طرفین روابط 4 و 5 رابطهٔ فیثاغورس را برای مثلث ABC نتیجه بگیرید.
\(B{C^2} = \;.....\; + \;.....\)
\(B{C^2} = \;A{B^2}\; + \;A{C^2}\)
8 مساحت مثلث ABC را به دو طریق محاسبه و با توجه به آن تساوی زیر را کامل کنید.
\(AB \times \;.... = AH \times ....\)
\(AB \times \;AC = AH \times BC\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















