1736019749.png)
گام به گام تمرین صفحه 56 درس 3 ریاضی یازدهم (تابع)
تعداد بازدید : 60.99Mپاسخ تمرین صفحه 56 ریاضی یازدهم
-گام به گام تمرین صفحه 56 درس تابع
-تمرین صفحه 56 درس 3
-1 نمودار تابع با ضابطهٔ \(f(x) = \frac{1}{x}\)و با دامنه \({D_f} = \left[ { - 5\,,\,5} \right] - \left\{ 0 \right\}\) را رسم کنید.
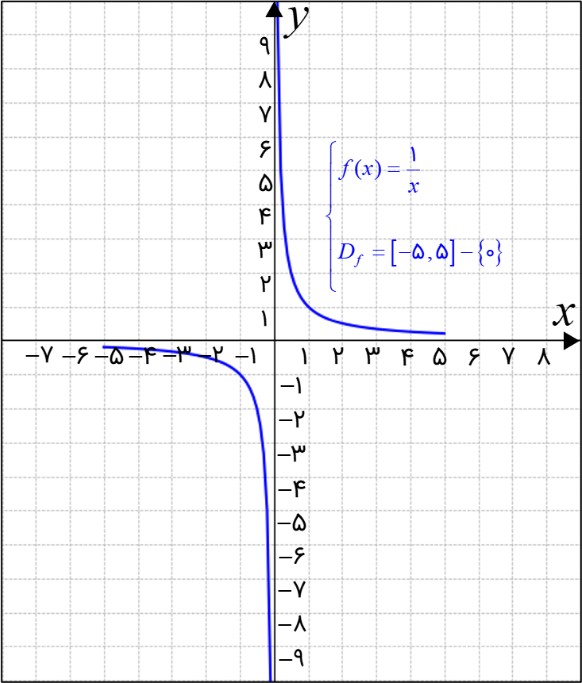
توضیح تکمیلی (برای بهتر درک کردن مسئله):
تابع \(f(x) = \frac{1}{x}\) یک تابع هموگرافیک است. فرم اصلی تابع هموگرافیک به صورت زیر می باشد:
تابع هموگرافیک:
\(f(x) = \frac{{ax + b}}{{cx + d}}\)
برای کشیدن این تابع به صورت زیر عمل می کنیم:
1- ابتدا خط \(y = \frac{a}{c}\) را به صورت خط چین بکشید.
2- سپس خط \(x = - \frac{d}{c}\) را به صورت خط چین بکشید.
3- با توجه به مقدار محاسبه شده ی \(ad - bc\) نمودار تابع متفاوت می باشد:
\(ad - bc > 0\) (الف
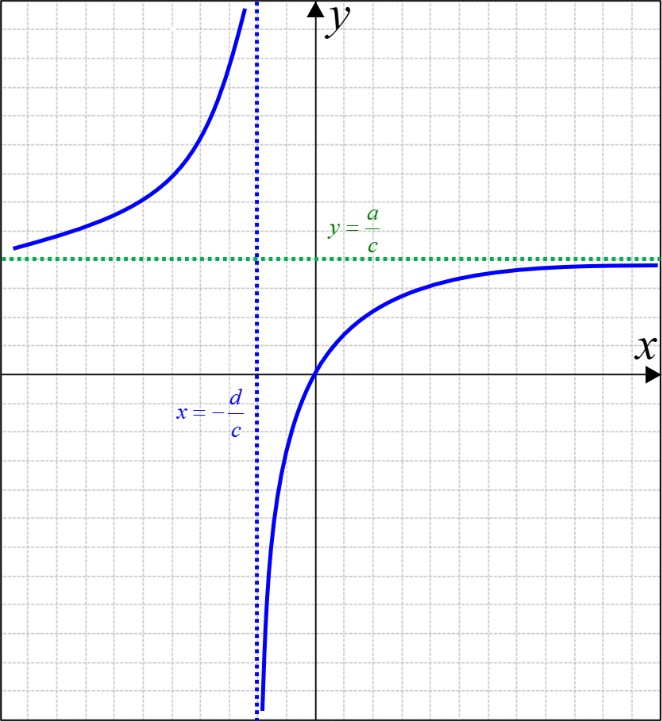
\(ad - bc < 0\) (ب
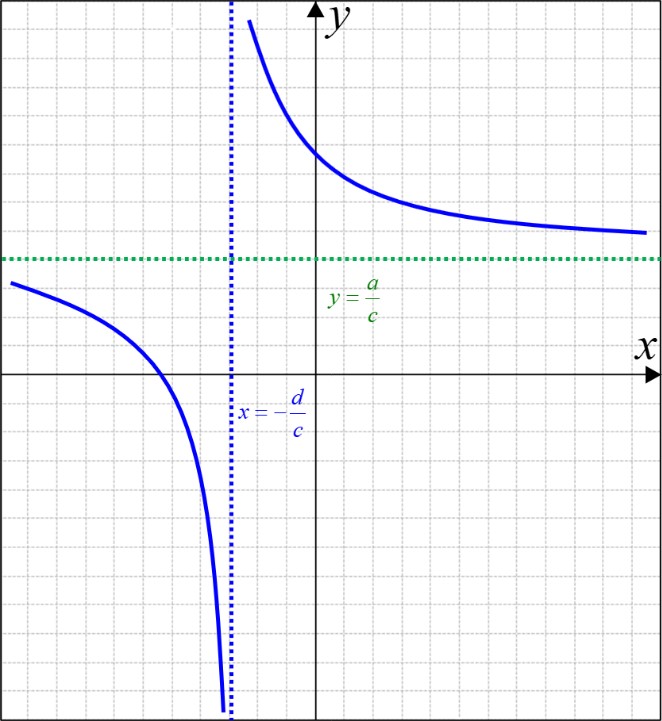
\(ad - bc = 0\) (پ
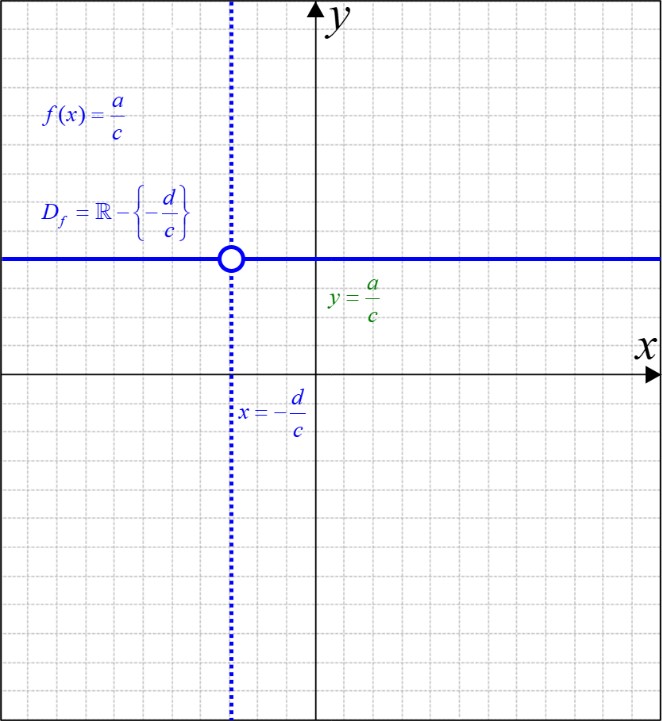
در این حالت تابع هموگرافیک به صورت \(f(x) = \frac{a}{c}\) می باشد و دامنه آن \({D_f} = \mathbb{R} - \left\{ { - \frac{d}{c}} \right\}\) می باشد.
2 دامنهٔ تابع گویای با ضابطهٔ \(f(x) = \frac{{x + 3}}{{x - 3}}\) را به دست آورید.
کافی است عددی که مخرج کسر با آن عدد برابر صفر می شود را از مجموعه اعداد حقیقی حذف کنیم؛ یعنی:
\({D_f} = \mathbb{R} - \left\{ 3 \right\}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای تعیین دامنه هر تابع، بهترین راه تعیین علامت کردن آن تابع است. از نقاط یا بازه هایی که تابع تعریف می شود، دامنه تابع بدست می آید.
پس تابع \(f(x) = \frac{{x + 3}}{{x - 3}}\) را تعیین علامت می کنیم:
ابتدا x هایی را که در آن عبارت های x+3 و x-3 برابر صفر می شوند را بدست می آوریم و سپس جدول تعیین علامت را تشکیل می دهیم:
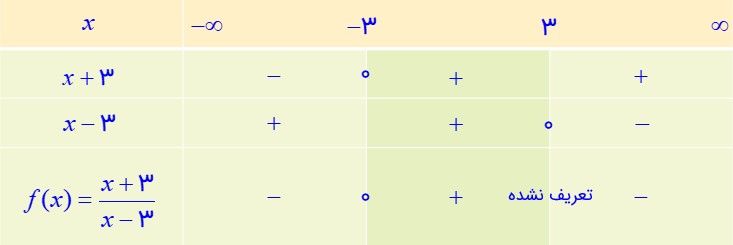
همانطور که در جدول تعیین علامت می بینین، تابع \(f(x) = \frac{{x + 3}}{{x - 3}}\) به ازای همه مقادیر x به جز مقدار x=3 مقدار دارد. بنابراین دامنه تابع مورد نظر برابر \({D_f} = \mathbb{R} - \left\{ 3 \right\}\) می شود.
3 در هر مورد آیا دو تابع داده شده با هم برابرند؟
\(f(x) = \left\{ \begin{array}{l} - 1\,\,\,\,\,\,\,\,\,\,x < 0\\\\\,\,\,1\,\,\,\,\,\,\,\,\,\,x < 0\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,g(x) = \frac{{\left| x \right|}}{x}\) (الف
دامنه این تابع با هم برابر است:
\({D_f} = {D_g} = \mathbb{R} - \left\{ 0 \right\}\)
پس از ساده کردن تابع g ، مشاهده می کنیم که این دو تابع با هم برابرند:
\(\left. \begin{array}{l}x > 0 \Rightarrow g(x) = \frac{{\left| x \right|}}{x} = \frac{x}{x} = 1\\\\x < 0 \Rightarrow g(x) = \frac{{\left| x \right|}}{x} = \frac{{ - x}}{x} = - 1\end{array} \right\} \Rightarrow g(x) = \left\{ \begin{array}{l} - 1\,\,\,\,\,\,\,\,\,\,x < 0\\\\\,\,\,1\,\,\,\,\,\,\,\,\,\,x < 0\end{array} \right.\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای اینکه دو تابع f و g با یکدیگر برابر باشند، بایستی دو شرط زیر برای این دو تابع برقرار باشد:
اولین شرط؛ تبدیل شدن دو تابع به یکدیگر؛ یعنی اینکه بایستی یکی از توابع f یا g با ساده کردن به آن یکی دیگر تبدیل شود.
شرط دوم اینکه بایستی دامنه هر دو تابع با هم برابر باشند؛ یعنی \({D_f} = {D_g}\)
توجه کنید که اگر دو تابع f و g ، حتی در یک نقطه با یکدیگر برابر نباشند، مثلا در دامنه یکی از این توابع تعریف نشده باشد، هرگز برابر با یکدیگر نمی شوند. دقیقاً مانند مسئله ب!
\(f(x) = x - 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,g(x) = \frac{{{x^2} - 4}}{{x + 2}}\) (ب
ابتدا تابع g را ساده می کنیم:
\(g(x) = \frac{{{x^2} - 4}}{{x + 2}} = \frac{{(x + 2)(x - 2)}}{{x + 2}} = x - 2\)
تا اینجا تابع g با ساده سازی تبدیل به تابع f شد. حال بیایید بررسی کنیم ببینیم که آیا دامنه هر دو تابع یکی است!
دامنه هر تابع برابر خواهد بود با:
\(\left\{ \begin{array}{l}{D_f} = \mathbb{R}\\\\{D_g} = \mathbb{R} - \left\{ { - 2} \right\}\end{array} \right. \Rightarrow {D_f} \ne {D_g}\)
بخاطر اینکه شرط دوم برای دو تابع برقرار نیست، بنابراین دو تابع f و g با هم برابر نخواهند بود.
4 تابعی گویا بنویسید که دامنه اش برابر \(\mathbb{R} - \left\{ { - 1} \right\}\) شود. پاسخ خود را با جواب دوستانتان مقایسه کنید.
\(g(x) = \frac{{{x^2} - 1}}{{x + 1}}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
بی نهایت تابع می توان مثال زد. اما همه این توابع در این ویژگی هایی که می گویم صدق می کنند:
اول اینکه در صورت یک چند جمله ای از هر درجه ای می تواند باشد. طبیعتا در یک چند جمله ای فقط x های با توان مثبت و یک عدد ثابت وجود دارد؛ نه تابعی رادیکالی یا مثلثاتی و یا دارای جزء صحیح!
دوم اینکه در مخرج هم فقط تابع درجه یک از عبارت x+1 وجود دارد؛ مثلاً:
\(\begin{array}{l}x + 1\\\\2(x + 1)\\\\ - 3/5(x + 1)\\\\\pi (x + 1)\end{array}\)
5 ابتدا دامنهٔ تابع با ضابطهٔ \(g(x) - 3 + \sqrt {x - 4} \) را به دست آورده، سپس نمودار آن را رسم کنید.
برای اینکه دامنه تابع g را بدست آوریم، کافی است که زیر رادیکال را بزرگتر یا مساوی صفر قرار دهیم و دامنه را بدست آوریم:
\(x - 4 \ge 0 \Rightarrow x \ge 4 \Rightarrow {D_g} = \left[ {4\,,\,\infty } \right)\)
نمودار تابع g به صورت زیر می شود:
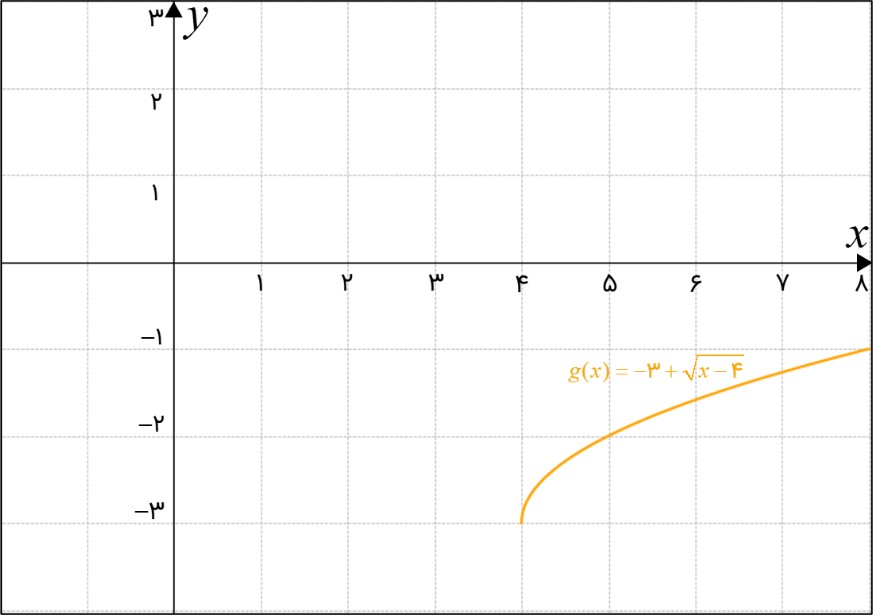
توضیح تکمیلی (برای بهتر درک کردن مسئله):
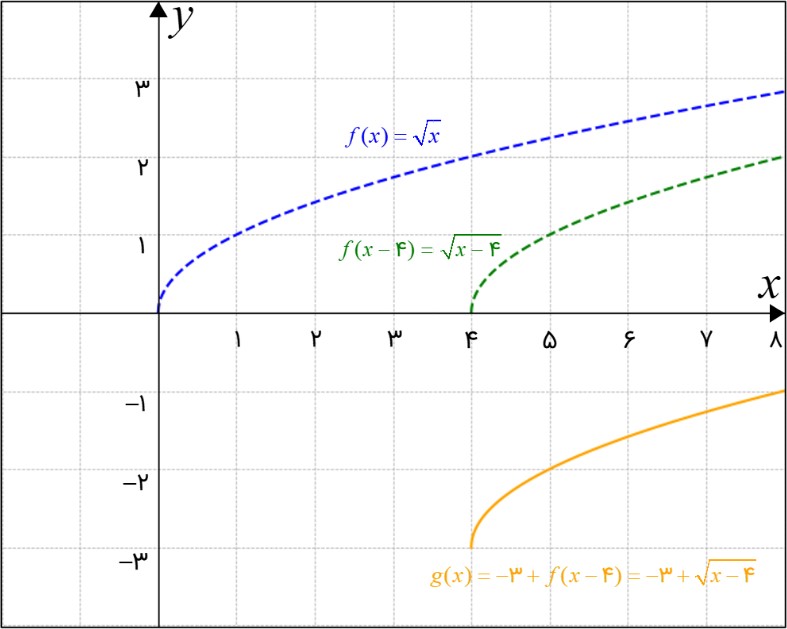
برای اینکه تابع g را رسم کنیم، بهتر است ابتدا تابع \(f(x) = \sqrt x \) را رسم کنیم.
سپس به سمت راست چهار واحد جابجا کنیم تا تابع \(f(x - 4) = \sqrt {x - 4} \) بدست آید.
سپس تابع انتقال داده شده را 3 واحد به سمت پایین جابجا می کنیم تا تابع g(x) بدست آید.
6 دامنهٔ توابع مقابل را به دست آورید:
\(h(x) = \sqrt {2x} + 1\) الف
\(\sqrt {2x} \ge 0 \Rightarrow 2x \ge 0 \Rightarrow x \ge 0 \Rightarrow {D_h} = \left[ {0\,,\,\infty } \right)\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای بدست آوردن توابع رادیکالی، کافی است که زیر رادیکال را بزرگتر یا مساوی صفر قرار دهید و سپس این نامساوی را حل نمایید تا دامنه ی این نوع توابع بدست آید.
علت اینکه زیر رادیکال باید بزرگتر یا مساوی صفر باشد، چیست؟
دو تا علت دارد:
اول اینکه زیر رادیکال نمی تواند منفی باشد (اصلی ترین علت!)
دوم اینکه همواره جواب رادیکال، عددی مثبت است؛ یعنی رادیکال هیچ وقت عدد منفی نمی دهد.
\(k(x) = \sqrt {1 - 4x} \) ب
\(\begin{array}{l}\sqrt {1 - 4x} \ge 0 \Rightarrow 1 - 4x \ge 0 \Rightarrow - 4x \ge - 1 \Rightarrow x \le \frac{{ - 1}}{{ - 4}}\\\\ \Rightarrow x \le \frac{1}{4} \Rightarrow {D_k} = \left[ {0\,,\,\infty } \right)\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
این هم دقیقا مثل مورد الف حل می شود، فقط دقت کنین که وقتی دو طرف نامساوی را بر عدد -4 تقسیم می کنید، به این علت که عددی منفی هست، جهت نامساوی تغییر می کند!
\(t(x) = \sqrt {{x^2} - x} \) پ
\(\sqrt {{x^2} - x} \ge 0 \Rightarrow {x^2} - x \ge 0\)
از اینجا به بعد قطعاً نیاز به تعیین علامت داریم. ابتدا ریشه های این معادله درجه دوم رو بدست می آوریم:
\({x^2} - x = 0 \Rightarrow x(x - 1) = 0 \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x - 1 = 0 \Rightarrow x = 1\end{array} \right.\)
حال تعیین علامت می کنیم:
پس دامنه تابع t برابر \({D_t} = \mathbb{R} - \left( {0\,,\,1} \right)\) می شود.
7 حاصل عبارت های مقابل را حساب کنید.
\(\left[ {300/4002} \right]\)
\(\left[ {300/4002} \right] = 300\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
تعریف جزء صحیح:
جزء صحیح یک عدد حقیقی، بزرگ‌ترین عدد صحیحی است که کوچکتر یا مساوی آن عدد باشد. این مفهوم در ریاضیات به صورت \(\left[ x \right]\) نمایش داده می شود.
\(n \le x < n + 1 \Rightarrow \left[ x \right] = n\)
برای همین مسئله، عدد 300/4002 بین دو عدد صحیح 300 و 301 قرار دارد؛ بنابراین داریم:
\(300 \le 300/4002 < 301 \Rightarrow \left[ {300/4002} \right] = 300\)
\(\left[ { - 103/003} \right]\)
\(\left[ { - 103/003} \right] = - 104\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای این مسئله نیز، عدد -103/003 بین دو عدد صحیح -104 و -103 قرار دارد؛ بنابراین داریم:
\( - 104 \le - 103/003 < - 103 \Rightarrow \left[ { - 103/003} \right] = - 104\)
\(\left[ { - 2309/54} \right]\)
\(\left[ { - 2309/54} \right] = - 2310\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
همچنین برای این مسئله، عدد -2309/54 بین دو عدد صحیح -2310 و -2309 قرار دارد؛ بنابراین داریم:
\( - 2310 \le - 2309/54 < - 2309 \Rightarrow \left[ { - 2309/54} \right] = - 2310\)
8 تابع پله ای روبه رو را رسم کنید.
\(f(x) = \left\{ \begin{array}{l}3\,\,\,\,\,\,\,\,\,\,x \in \left[ {0\,,\,1} \right)\\\\0\,\,\,\,\,\,\,\,\,\,x \in \left[ {1\,,\,5} \right]\\\\2\,\,\,\,\,\,\,\,\,\,x \in \left( {6\,,\,7} \right]\end{array} \right.\)
شکل نمودار به این صورت می شود:
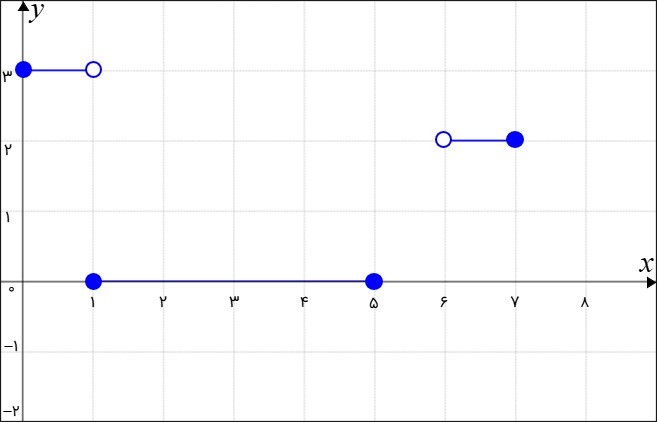
توضیح تکمیلی (برای بهتر درک کردن مسئله):
در نقاط ابتدایی و انتهایی بازه توجه کنید که دایره توپُر برای نقطه ای استفاده می شود که در آن نقطه براکت هست و دایره توخالی برای نقطه ای استفاده می شود که در آن نقطه پرانتز هست.
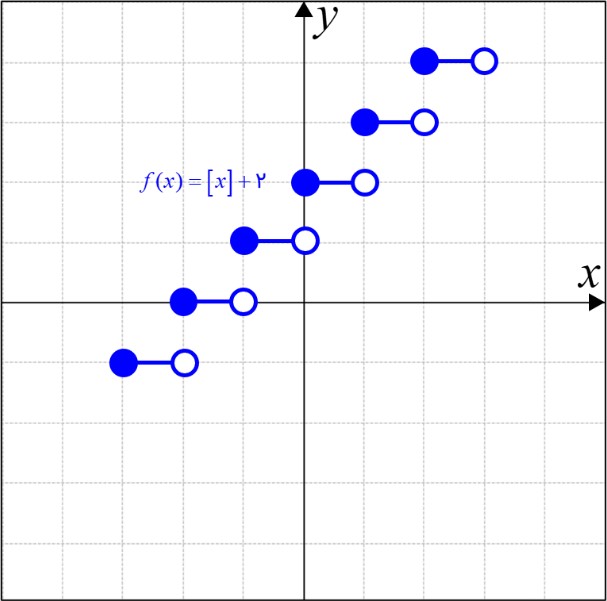
9 تابع با ضابطهٔ \(f(x) = \left[ x \right] + 2\) و دامنه \({D_f} = \left[ { - 3\,,\,3} \right)\) را رسم کنید.
\(\begin{array}{l}f(x) = \left[ x \right] + 2\quad ,\quad x \in \left[ { - 3\;,\;3} \right)\\\\ - 3 \le x < - 2 \Rightarrow \left[ x \right] = - 3 \Rightarrow f(x) = - 3 + 2 = - 1\\\\ - 2 \le x < - 1 \Rightarrow \left[ x \right] = - 2 \Rightarrow f(x) = - 2 + 2 = 0\\\\ - 1 \le x < 0 \Rightarrow \left[ x \right] = - 1 \Rightarrow f(x) = - 1 + 2 = 1\\\\0 \le x < 1 \Rightarrow \left[ x \right] = 0 \Rightarrow f(x) = 0 + 2 = 2\\\\1 \le x < 2 \Rightarrow \left[ x \right] = 1 \Rightarrow f(x) = 1 + 2 = 3\\\\2 \le x < 3 \Rightarrow \left[ x \right] = 2 \Rightarrow f(x) = 2 + 2 = 4\end{array}\)
شکل این تابع به صورت زیر می شود:
توضیح تکمیلی (برای بهتر درک کردن مسئله):
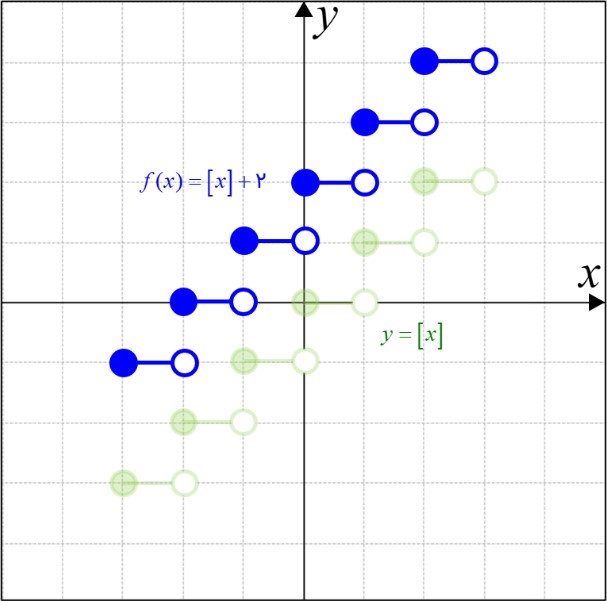
روش دیگری برای رسم این تابع وجود دارد. آن روش این است:
کافی است که تابع جزء صحیح را در بازه ی \(\left[ { - 3\,,\,3} \right)\) رسم کنیم و 2 واحد به سمت بالا جابجا کنیم:
\(\begin{array}{l}y = \left[ x \right]\\\\f(x) = y + 2 = \left[ x \right] + 2\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
