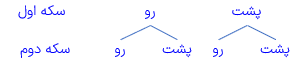
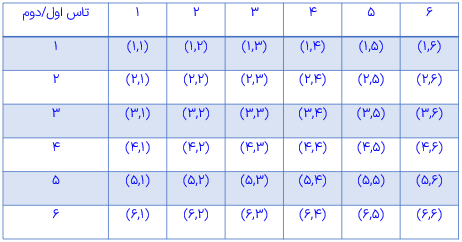
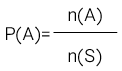درسنامه کامل ریاضی هشتم
تعداد بازدید : 240.65kخلاصه نکات ریاضی هشتم - درسنامه شب امتحان ریاضی هشتم - جزوه شب امتحان ریاضی هشتم نوبت اول
اعداد صحیح
فصل 1 : عددهای صحیح و گویا
اعداد صحیح
اعداد صحیح از سه دسته تشکیل شده اند:
اعداد مثبت، صفر واعداد منفی
اعداد صحیح را با حرف انگلیسی \(\mathbb{Z}\) نشان می دهند:
\(\mathbb{Z} = \left\{ { \cdots \,,\, - 2\,,\, - 1\,,\, \circ \,,\,1\,,\,2\,,\, \cdots } \right\}\)
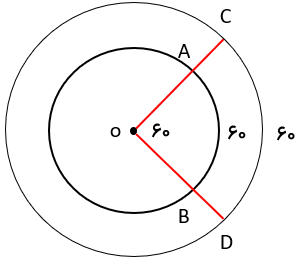
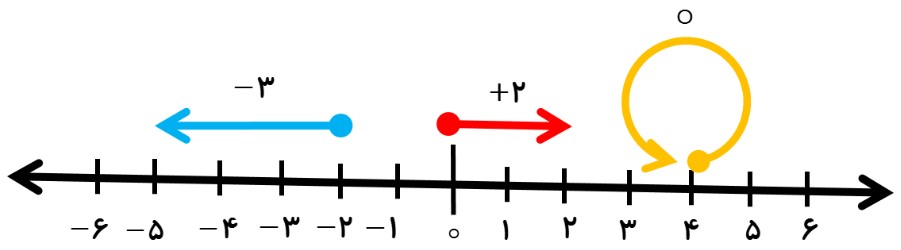
حرکت روی محور اعداد صحیح
جا به جایی از یک نقطه به نقطه ی دیگر را «حرکت» می گویند؛ اگر این حرکت در جهت مثبت (سمت راست) باشد، با علامت مثبت (+) و اگر در جهت منفی (سمت چپ) باشد، علامت منفی (-) خواهد داشت؛ به عنوان مثال:
قرینه
به اعدادی که فاصله آن ها تا «صفر» با هم برابر باشد، دو عدد قرینه می گویند؛ مانند 3+ و 3- ، 2+ و 2-.
10- = قرینه 10
5+ = قرینه 5-
1 قرینه را با علامت (−) نمایش می دهند. قرینه ی هر عدد صحیح را می توان با تغییر علامت آن بدست آورد.
8- = قرینه 8
3+ = قرینه 3-
2 قرینه ی عدد صفر برابر صفر می باشد.
-0=0
3 قرینه قرینه عر عدد خود عدد می باشد.
\(\begin{array}{l} - \left[ { - \,( - \,3)} \right] = - \,3\\\\ - \left[ { + \,( - \,6)} \right] = + \,6\end{array}\)
مثال
قرینه قرینه قرینه عدد 10 کدام است؟
هر کلمه قرینه را با نماد – نشان می دهیم:
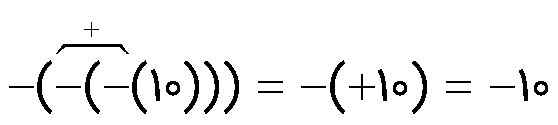
مثال
اگر عدد 25- را 1023 بار قرینه کنیم، نتیجه حاصل چه عددی می شود؟
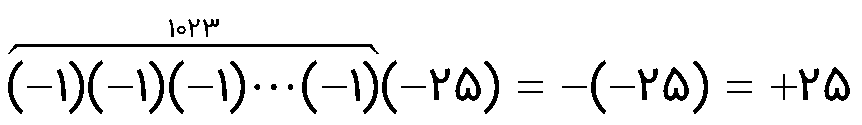
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
جمع و تفریق اعداد صحیح
فصل 1 : عددهای صحیح و گویا
جمع و تفریق اعداد صحیح
برای محاسبه ی حاصل جمع و یا تفریق عددهای صحیح ابتدا مختصر نویسی (ساده نویسی) می کنیم، به این صورت که پرانتزها رو حذف کرده، سپس اگر عددی بیشتر از یک علامت داشته باشد، علامت های آن ها را در هم ضرب می کنیم تا به یک علامت تبدیل شود. آنگاه با یکی از دو حالت زیر مواجه می شویم:
1- حالت اول:
عددها هم علامت باشند؛ در این حالت یکی از علامت ها را نوشته، سپس عددها را با هم جمع می کنیم؛ مانند:
10- = (7–) + (3–)
14+ = 6 + 8+ = (6–) – (8+)
2- حالت دوم:
عددها هم علامت نباشند؛ در این حالت علامت عددی که بزرگتر است (بدون در نظر گرفتن علامت( را نوشته سپس عددها را از هم کم می کنیم؛ مانند:
2+ = 8 + 6- = (8+) + (6-)
5- = 30 - 25 = (30+) - 25
اگر تعداد عددها بیشتر از دو تا بود، می توان عددهای مثبت را با هم و عددهای منفی را با هم جمع کرد، سپس حاصل نهایی را بدست آورد.
مثال
حاصل عبارت زیر را بدست آورید.
= 7 + (3+) - (6+) + 4-
6+ = 13 + 7- = 7 + 3 - 6 + 4- = 7 + (3+) - (6+) + 4-
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
ضرب و تقسیم اعداد صحیح
فصل 1 : عددهای صحیح و گویا
ضرب و تقسیم اعداد صحیح
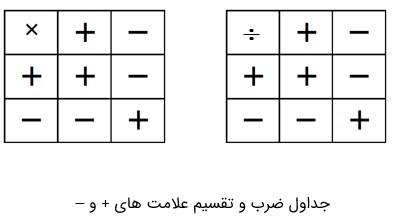
ابتدا علامت ها را در هم ضرب کرده، سپس اعداد را با توجه به علامت بین آن ها ضرب یا تقسیم می کنیم.
جدول ضرب علامت ها
مثال
حاصل ضرب و تقسیم های زیر را بیابید.
= (3-) ÷ [(4+) × (6-)] (1
= [(4+) ÷ 12] × 8- (2
8+ = (3-) ÷ (24-)= (3-) ÷ [(4+) × (6-)] (1
24- = (2+) × (8-) = [(4+) ÷ 12] × 8- (2
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
اولویت های انجام عملیات در ریاضی
فصل 1 : عددهای صحیح و گویا
اولویت های انجام عملیات در ریاضی
برای محاسبه ی عبارت ترکیبی جمع، تفریق، ضرب، تقسیم باید بر اساس ترتیب اولویت ها شروع به پاسخ دادن کرد:
1( مجموعه یا کروشه یا پرانتز
2( توان و جذر
3( ضرب و تقسیم (از سمت چپ)
4) جمع و تفریق
مثال
حاصل عبارت مقابل را به دست آورید.
\(4 - 4 \times {3^2} \div 6 - (9 - {2^3}) = \)
ابتدا حاصل داخل پرانتز را محاسبه می کنیم:
\(9 - {2^3} = 9 - 8 = 1\)
حال داریم:
\(4 - 4 \times {3^2} \div 6 - 1 = \)
سپس از سمت چپ مطابق ترکیب عملیات پیش می رویم (توان و جذر):
\(4 - 4 \times 9 \div 6 - 1 = \)
مجدد از سمت چپ طبق ترتیب عملیات پیش می رویم:
\(4 - 36 \div 6 - 1 = 4 - 6 - 1 = - 3\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
جمع اعداد یک مجموعه منظم
فصل 1 : عددهای صحیح و گویا
جمع اعداد یک سری (مجموعه) منظم
برای جمع اعداد یک سری منظم، از رابطه های زیر استفاده می کنیم:
مثال
حاصل عبارت های زیر را به دست آورید.
\(3 + 6 + 9 + \cdots + 204 = \)
\( = \,\,\frac{{204 - 3}}{3} + 1 = 67 + 1 = 68\) تعداد اعداد
\( = \,\,\frac{{204 + 3}}{2} \times 68 = 207 \times 34 = 7038\) مجموع اعداد
برای جمع اعداد یک سری منظم که یک در میان مثبت و منفی باشند ابتدا دو به دو اعداد را جواب می دهیم؛ مانند:
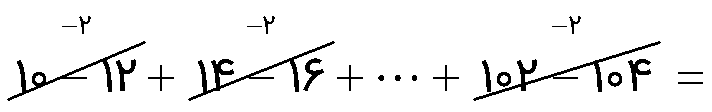
\( = \,\,\frac{{104 - 10}}{2} + 1 = 47 + 1 = 48\) تعداد اعداد
\(\begin{array}{l}48 \div 2 = 24\\\\10 - 12 + 14 - 16 + \cdots + 102 - 104 = 24 \times ( - 2) = - 48\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
اعداد گویا
فصل 1 : عددهای صحیح و گویا
اعداد گویا
هر عدد را که بتوان به صورت یک کسر نوشت، به طوری که صورت و مخرج آن عدد صحیح بوده و مخرج آن صفر نباشد را عدد گویا می نامند.
اعداد گویا را با حرف انگلیسی \(\mathbb{Q}\) نمایش می دهند:
\(\mathbb{Q} = \left\{ {\left. {\frac{a}{b}} \right|a\,,\,b\, \in \mathbb{Z}\,,\,b \ne \circ } \right\}\)
عددهای طبیعی، حسابی، صحیح، کسری، اعشاری، مخلوط و رادیکال هایی که عدد زیر رادیکال آن مجذور کامل باشد یک عدد گویا می باشند؛ مانند:
\(\begin{array}{l} - \frac{5}{6}\,\,\,\,\,\,\,\,\,13 = \frac{{13}}{1}\,\,\,\,\,\,\,\,\,\frac{8}{{ - 3}}\,\,\,\,\,\,\,\,\,0/7 = \frac{7}{{10}}\,\,\,\,\,\,\,\,\, - 2\frac{3}{4}\\\\\sqrt {25} = 5 = \frac{5}{1}\,\,\,\,\,\,\,\,\, \circ = \frac{ \circ }{1}\end{array}\)
اگر مخرج کسری صفر باشد، کسر را «تعریف نشده» می نامند.
نمایش اعداد گویا روی محور
برای نمایش هر عدد گویا روی محور طبق مراحل زیر عمل می کنیم:
1) واحدهای محور را به تعداد عدد مخرج کسر تقسیم می کنیم.
2) با توجه به علامت عدد، جهت حرکت را مشخص می کنیم، علامت + حرکت به سمت راست و علامت − حرکت به سمت چپ است.
3) به تعداد عدد صورت کسر از صفر ، واحدهای تقسیم شده را شمارش می کنیم.
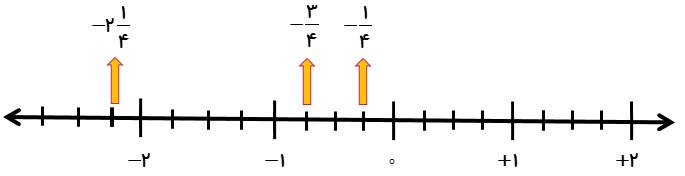
مثال
عددهای مقابل را مانند نمونه روی محور نمایش دهید.
\( - \frac{3}{4}\,\,\,\,\,,\,\,\,\,\,\frac{1}{4}\,\,\,\,\,,\,\,\,\,\, - 2\frac{1}{4}\)
1 قرینه ی اعداد گویا همانند قرینه عددهای صحیح می باشد؛ مانند:
\( - ( - \frac{7}{5}) = + \frac{7}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - ( + \frac{2}{3}) = - \frac{2}{3}\)
2 برای نوشتن معکوس اعداد گویا ، جای صورت و مخرج آن را عوض می کنیم:
\( - \frac{{11}}{6}\,\, \to \,\, - \frac{6}{{11}}\,\,\,\,\,\,\,,\,\,\,\,\,\, - 4\frac{2}{3} = - \frac{{14}}{3}\,\, \to \,\, - \frac{3}{{14}}\)
3 علامت کسر را می توان در کنار خود کسر، کنار صورت و یا کنار مخرج کسر نوشت. به محور زیر دقت کنید. می دانیم \(\frac{{ - 3}}{2}\) یعنی 2 ÷ 3- . برای نمایش این عدد برداری به طول 3- رسم می کنیم و آن را به دو قسمت مساوی تقسیم می کنیم. هر تکه برداری در جهت منفی محور اعداد و به طول \(\frac{3}{2}\) واحد است. پس عدد متناطر با هر قسمت کوچک \(\frac{{ - 3}}{2}\) است. بنابراین داریم:
\(\frac{{ - 3}}{2} = - 3 \div 2 = - \frac{3}{2}\)
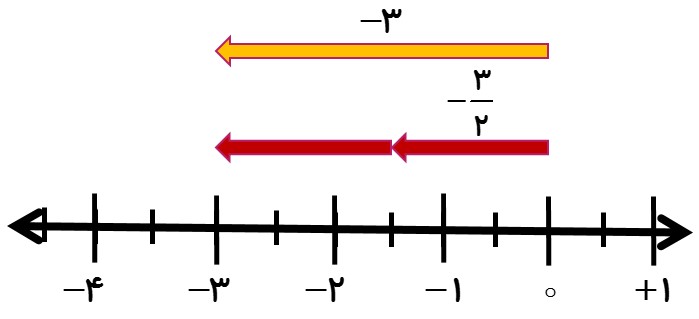
مثال
تساوی \(\frac{{ - 5}}{3} = - \frac{5}{3}\) را به کمک محور کامل کنید.
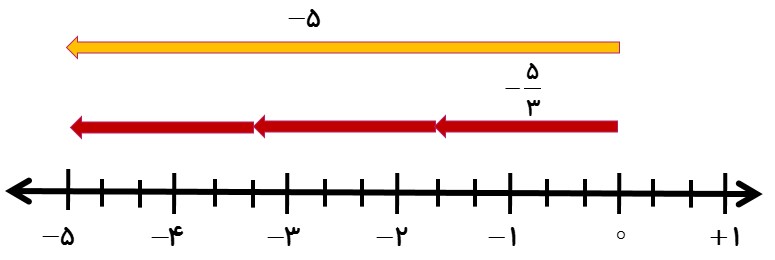
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
محدوده ی اعداد
فصل 1 : عددهای صحیح و گویا
محدوده ی اعداد
اعداد بزرگتر از 2 را به صورت \(x > 2\) نمایش می دهیم و شامل تمامی اعدادی است که از 2 بزرگترند.
اعداد بزرگتر یا مساوی با 2 را به صورت \(x \ge 2\) نمایش می دهیم و شامل عدد 2 و همه ی اعداد بزرگتر از 2 است.
اعداد بین 1 و 2 را به صورت \(1 < x < 2\) نمایش می دهیم.
اعداد کوچکتر یا مساوی با 2 و بزرگتر از 1 را با \(1 < x \le 2\) نمایش می دهند و شامل عدد 2 و تمام اعداد بین 1 و 2 است.
مثال
برای هر کدام از محدوده های زیر دو عدد مثال بزنید.
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تساوی کسرها
فصل 1 : عددهای صحیح و گویا
تساوی کسرها
اگر صورت و مخرج کسر را در عددی غیر از صفر ضرب کنیم، یا بر عددی غیر از صفر تقسیم کنیم، کسر حاصل با کسر اول مساوی می باشد؛ مانند:
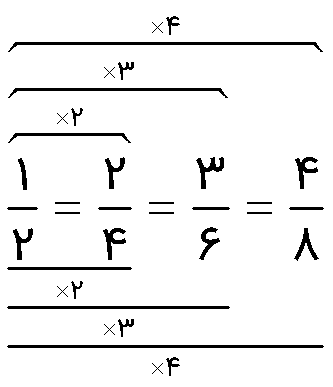
مثال
برای کسر زیر 2 کسر مساوی بنویسید.
\(\frac{3}{5} = \)
\(\frac{3}{5} = \frac{6}{{10}} = \frac{9}{{15}}\)
در تساوی دو کسر اگر یکی از عددها مجهول باشد، به کمک تساوی کسرها می توان مقدار مجهول را به دست آورد.
مانند نمونه مقدار مجهول را به دست آورید.
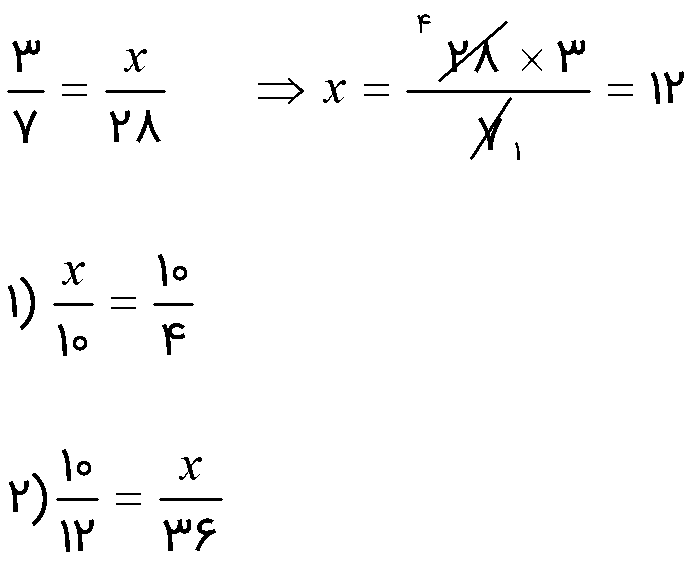
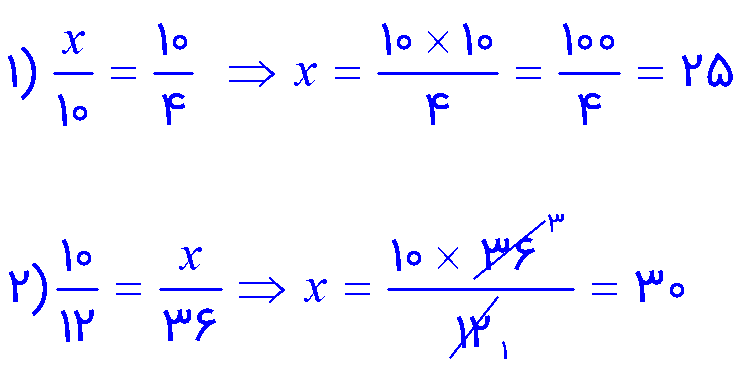
1 برای اینکه یک کسر را تا حد ممکن ساده کنیم باید صورت و مخرج آن را بر «ب.م.م» صورت و مخرج تقسیم کنیم.
2 برای به دست آوردن ب.م.م، ابتدا دو عدد را به عامل های اول تجزیه می کنیم، سپس حاصل ضرب عامل های مشترک دو عدد با توان کمتر را حساب می کنیم.
مثال
کسر زیر را مانند نمونه تا حد امکان ساده کنید.
\(\begin{array}{l}\frac{{ - 56}}{{210}} = \\\\\frac{{48}}{{100}} = \end{array}\)
\(\begin{array}{l}56 = {2^3} \times 7\\\\210 = 2 \times 3 \times 5 \times 7\\\\\left( {56\,,\,210} \right) = 2 \times 7 = 14\\\\\frac{{ - 56}}{{210}} = \frac{{ - 56 \div 14}}{{210 \div 14}} = \frac{{ - 4}}{{15}}\\\\ - - - - - - - - - - - - - - - - - \\48 = {2^4} \times 3\\\\100 = {2^2} \times {5^2}\\\\\left( {48\,,\,100} \right) = {2^2} = 4\\\\\frac{{48}}{{100}} = \frac{{48 \div 4}}{{100 \div 4}} = \frac{{12}}{{25}}\end{array}\)
1 از تساوی کسرها می توان نتیجه گرفت که هر کسر گویا بی شمار نمایش مختلف دارد.
2 نوشتن عددی گویا بین دو عدد به چند روش است که یک روش کاربردی آن در زیر آورده شده ابتدا مخرج مشترک گرفته سپس صورت و مخرج را در یک واحد بیشتر از تعداد کسرهای خواسته شده ضرب می کنیم.
3 با توجه به تقسیم شدن فاصله ی بین دو عدد، کسرهای مختلفی بین هر دو عدد صحیح می توان نوشت.
4 بین هر دو عدد کسری نیز می توان کسرهای بی شماری پیدا کرد.
مثال
ما بین دو عدد گویای زیر دو عدد گویا (دو کسر) پیدا کنید.
\(\frac{3}{4}\,\,,\,\,\frac{5}{7}\)
\(\begin{array}{l}\left. \begin{array}{l}\frac{3}{4} = \frac{{21}}{{28}} = \frac{{21 \times 3}}{{28 \times 3}} = \frac{{63}}{{84}}\\\\\frac{5}{7} = \frac{{20}}{{28}} = \frac{{20 \times 3}}{{28 \times 3}} = \frac{{60}}{{84}}\,\end{array} \right\}\\\\ \Rightarrow \frac{5}{7} = \frac{{60}}{{84}} < \frac{{61}}{{84}} < \frac{{62}}{{84}} < \frac{{63}}{{84}} = \frac{3}{4}\\\\ \Rightarrow \frac{5}{7} < \frac{{61}}{{84}} < \frac{{62}}{{84}} < \frac{3}{4}\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
جمع و تفریق اعداد گویا
فصل 1 : عددهای صحیح و گویا
جمع و تفریق اعداد گویا
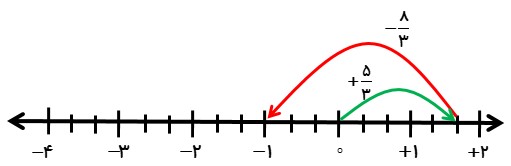
1- روش اول با استفاده از محور:
از حرکت های علامت دار روی محور استفاده می کنیم:
\(( + \frac{5}{3}) + ( - \frac{8}{3}) = - \frac{3}{3} = - 1\)
2- روش دوم:
الف) هنگامی که دو عدد گویا دارای مخرج های برابر باشند، جمع و تفریق آن ها به سادگی و مانند عددهای صحیح صورت می گیرد:
\(\begin{array}{l}\frac{3}{4} + \frac{5}{4} = \frac{{3 + 5}}{4} = \frac{8}{4} = 2\\\\\frac{7}{3} - \frac{5}{3} = \frac{{7 - 5}}{3} = \frac{2}{3}\end{array}\)
ب) در صورتی که مخرج ها یکسان نباشند، ابتدا مخرج ها را با استفاده از مخرج کسر دیگر یکسان می کنیم (ک.م.م(، سپس مانند قبل محاسبات جمع و یا تفریق را انجام می دهیم.
\(\frac{2}{3} + \frac{3}{4} = \frac{{2 \times 4}}{{3 \times 4}} + \frac{{3 \times 3}}{{4 \times 3}} = \frac{8}{{12}} + \frac{9}{{12}} = \frac{{17}}{{12}}\)
روش بدست آوردن ک.م.م
ابتدا هر عدد را به عامل های اول تجزیه می کنیم سپس عامل های مشترک هر دو عدد را در عامل های غیر مشترک ضرب می کنیم.
\(\begin{array}{l}\left[ {8\,,\,12} \right] = ?\\\\\left. \begin{array}{l}8 = {2^3}\\12 = {2^2} \times 3\end{array} \right\} \Rightarrow \left[ {8\,,\,12} \right] = 24\end{array}\)
مثال
حاصل عبارت مقابل را بدست آورید.
\( - \frac{2}{3} - (\frac{4}{{15}}) = \)
\(\begin{array}{l}\left[ {10\,,\,15} \right] = 30\\\\ \Rightarrow - \frac{2}{3} - (\frac{4}{{15}}) = \frac{{ - 9 + 8}}{{30}} = - \frac{1}{{30}}\end{array}\)
بهترین مخرج مشترک دو کسر ، همان ک.م.م عددهای مخرج هاست .
مثال
حاصل عبارت های زیر را به دست آورید.
\(\begin{array}{l}1)\,\,\frac{8}{{12}} - \frac{{12}}{{16}} = \\\\2)\, - \frac{7}{4} - ( - \frac{{13}}{4}) = \end{array}\)
\(\begin{array}{l}1)\,\,\left[ {12\,,\,16} \right] = 48\\\\ \Rightarrow \frac{8}{{12}} - \frac{{12}}{{16}} = \frac{{32 - 36}}{{48}} = - \frac{4}{{48}} = - \frac{1}{{12}}\\\\2)\, - \frac{7}{4} - ( - \frac{{13}}{4}) = \frac{{ - 7 + 13}}{4} = \frac{6}{4} = \frac{3}{2}\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
ضرب اعداد گویا
فصل 1 : عددهای صحیح و گویا
ضرب اعداد گویا
هنگام ضرب دو عدد گویا مراحل زیر انجام می شود:
1) ابتدا صورت را با مخرج یا بالعکس ساده کنید. (در صورت امکان)
2) علامت های دو عدد را طبق قانون ضرب علامت ها در هم ضرب کنید.
3) سپس صورت های دو کسر را در هم و مخرج ها نیز در هم ضرب کنید.
4) در ضرب اعداد گویا، اگر عددی مخلوط بود، ابتدا عدد مخلوط را به کسر تبدیل کنید.
مثال
حاصل عبارات زیر را بدست آورید.
\(\begin{array}{l}1)\,\,( - \frac{3}{5}) \times ( + \frac{7}{9}) = \\\\2)\,( - \frac{{20}}{{21}}) \times ( + \frac{{28}}{{80}}) = \end{array}\)
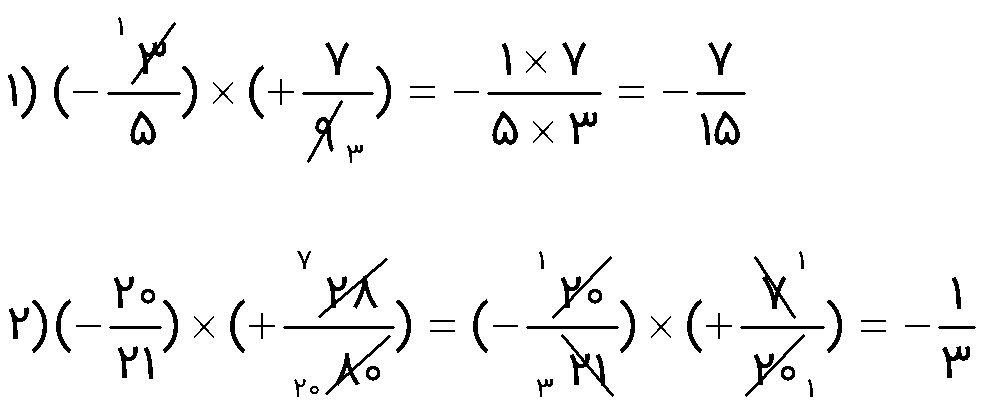
اگر در ضرب اعداد گویا عددی، عدد مخلوط بود ابتدا عدد مخلوط را به کسر تبدیل کنید؛ به عنوان مثال:
\(2\frac{3}{5} = \frac{{2 \times 5 + 3}}{5} = \frac{{13}}{5}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تقسیم اعداد گویا
فصل 1 : عددهای صحیح و گویا
تقسیم اعداد گویا
هنگام تقسیم دو عدد گویا مراحل زیر را انجام دهید.
1) کسر اول را بدون تغییر بنویسید.
2) علامت تقسیم را به ضرب تبدیل کرده و کسر دوم را به صورت معکوس بنویسید.
3) ضرب به دست آمده را انجام دهید.
به عنوان مثال:
\(( - \frac{3}{5}) \div \left( { + \frac{7}{4}} \right) = ( - \frac{3}{5}) \times \left( { + \frac{4}{7}} \right) = - \frac{{3 \times 4}}{{5 \times 7}} = - \frac{{12}}{{35}}\)
1 اگر جای صورت و مخرج یک کسر را تغییر دهیم معکوس آن کسر به دست می آید.
2 ساده کردن کسر ها در تقسیم بعد از اینکه به ضرب تبدیل شد الزامی است.
3 در صورت وجود عدد مخلوط ایتدا به کسر تبدیل کنید.
حل کنید.
\(( - \frac{3}{5}) \div \left( {\frac{2}{{15}}} \right) = \)
\(( - \frac{3}{5}) \div \left( {\frac{2}{{15}}} \right) = ( - \frac{3}{5}) \times \left( {\frac{{15}}{2}} \right) = - \frac{{3 \times 15}}{{10}} = - \frac{{3 \times 5}}{2} = - \frac{{15}}{2}\)
تقسیم \(\frac{2}{5} \div \frac{3}{8}\) را در نظر بگیرید. این تقسیم را می توان به صورت \(\frac{{\,\,\frac{2}{5}\,\,}}{{\frac{3}{8}}}\) نیز نوشت. محاسبه این کسر با ضرب عدد های مشخص شده انجام می شود؛ یعنی ضرب عدد های دور را در صورت و ضرب عدد های نزدیک را در مخرج می نویسیم. به این عمل «دور در دور _ نزدیک در نزدیک» گفته می شود:
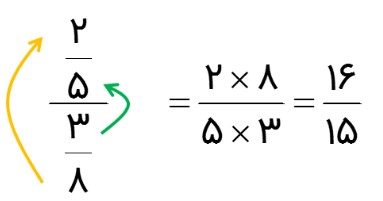
حل کنید.
\(\frac{{\frac{9}{5}}}{{ - \frac{{12}}{{15}}\,\,}} = \)
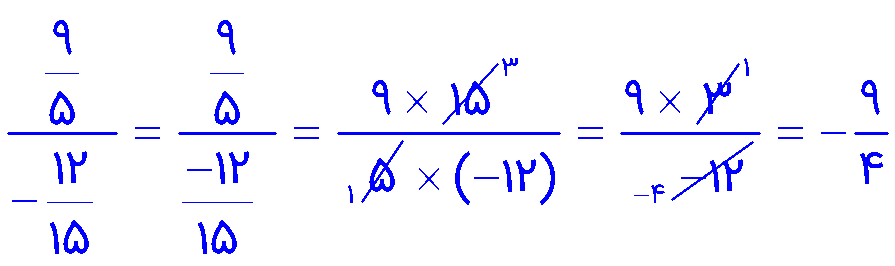
1 تنها عددی که معکوس ندارد عدد صفر است.
2 حاصل ضرب هر عدد در معکوس خودش برابر 1 می شود.
3 معکوس عدد 1 خود عدد یک می شود.
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
تشخیص اول یا مرکب بودن هر عدد طبیعی
فصل 2 : عددهای اول
تشخیص اول یا مرکب بودن هر عدد طبیعی
مطابق روش غربال باید مشخص شود عدد مورد نظر مضرب عدد های اول می باشد یا خیر. برای تشخیص ، باید عدد مورد نظر را بر اعداد اول مانند ... و 7 و 5 و 3 و 2 تقسیم کرد:
الف) اگر عدد داده شده بر یکی یا بیشتر ، از اعداد اول بخش پذیر باشد (باقیمانده صفر شود)، عدد داده شده مرکب است.
ب) اگر عدد داده شده بر هیچ کدام از اعداد اول بخش پذیر نباشد (باقیمانده صفر نشود)، عدد داده شده اول است.
برای تعیین تعداد این تقسیم ها ، از عدد مورد نظر جذر تقریبی می گیریم و سپس عدد داده شده را بر اعداد اول کوچکتر از جذر تقسیم می کنیم.
مثال
می خواهیم مشخص کنیم عدد 37 ، عدد اول است یا مرکب؟
ابتدا جذر تقریبی عدد 37 را می گیریم \((6 = \sqrt {36} < \sqrt {37} < \sqrt {49} = 7 \Rightarrow \sqrt {37} \simeq 6/1)\)
پس 37 را بر اعداد اول کوچکتر از 6 (یعنی 2، 3 و 5) تقسیم می کنیم:
یکان 37 فرد است پس بر 2 بخش پذیر نیست.
مجموع ارقام 37 عدد 10 است و بر 3 بخش پذیر نیست.
یکان 7 است و بر 5 بخش پذیر نیست (یکانش صفر یا 5 نیست).
چون بر هیچ کدام از اعداد اول 2 و 3 و 5 بخش پذیر نیست، بنابراین 37 یک عدد اول است.
مشخص کنید عدد 93 اول است یا مرکب؟
ابتدا جذر تقریبی عدد 93 را محاسبه می کنیم:
\(9 = \sqrt {81} < \sqrt {93} < \sqrt {100} = 10 \Rightarrow \sqrt {93} \simeq 9/6\)
پس عدد 93 را بر عددهای اول کوچکتر از 9 (یعنی 2، 3، 5 و 7) تقسیم می کنیم:
یکان 93 فرد است پس بر 2 بخش پذیر نیست.
مجموع ارقام 93 عدد 12 است و بر 3 بخش پذیر است.
عدد 93 بر 3 بخش پذیر است، پس 93 یک عدد مرکب است.
عددی کمتر از 160 و بزرگتر از 130 می باشد. برای اینکه بفهمیم این عدد اول است یا خیر، حداکثر چند تقسیم انجام می دهیم؟ چرا؟
در اینجا چون عدد مورد نظر دقیقا مشخص نشده باید عدد بزرگتر در صورت سوال مد نظر قرار گیرد.
\(12 = \sqrt {144} < \sqrt {160} < \sqrt {169} = 13 \Rightarrow \sqrt {160} \simeq 12/6\)
پس بر اعداد اول کوچکتر از 12 باید تقسیم شود. یعنی بر 2 و 3 و 5 و 7 و 11 پس یعنی حداکثر 5 تقسیم.
توجه کنید که در تمرین بالا، فقط تعداد تقسیم ها پرسیده شده و هیچ تقسیمی انجام نمی شود زیرا عدد مورد نظر دقیقاً داده نشده است.
عددهای 1 تا 90 را نوشته و غربال کرده ایم. با توجه به آن به سوالات زیر پاسخ دهید:
الف اولین عددی که خط می خورد؟
عدد 1
ب اولین مضرب مرکب 7 که برای اولین بار خط می خورد؟
عدد 49
پ عدد 57 با مضرب کدام عدد خط می خورد؟
عدد 3
ت تمام مضرب های 5 که برای بار اول خط می خورند، را بنویسید.
25 – 35 – 55 – 65 – 85
یادآوری
فصل 2 : عددهای اول
شمارنده (مقسوم علیه) یک عدد
شمارنده ها همان اعدادی هستند که عدد داده شده بر آنها بخش پذیر می شود؛ به عنوان مثال شمارنده های عدد 15، اعداد 1، 3، 5 و 15 هستند.
عدد اول
هر عدد طبیعی بزرگتر از یک که هیچ شمارنده طبیعی به جز خودش و یک نداشته باشد، عدد اول نامیده می شود؛ مانند اعداد 5 و 7:
شمارنده های 5، اعداد 1 و 5 هستند.
5 = 5 × 1
شمارنده های 7، اعداد 1 و 7 هستند.
7 = 7 × 1
عدد مرکب
هر عدد طبیعی بزرگتر از یک که بتوان آن را به صورت حاصل ضرب دو عدد طبیعی بزرگتر از یک نوشت ، عدد مرکب می نامند؛ مانند اعداد 30 و 6:
شمارنده های عدد 30:
15 × 2 = 10 × 3 = 6 × 5 = 30
شمارنده های عدد 6:
3 × 2 = 6
1 عدد یک، نه اول است و نه مرکب. ( زیرا فقط یک شمارنده دارد؛ یعنی خود یک)
2 هر عدد اول دقیقا دو شمارنده دارد.
3 هر عدد مرکب بیش از دو شمارنده دارد.
4 عدد یک، شمارنده ی همه عددهای طبیعی است.
5 بزرگترین شمارنده هر عدد، خود عدد است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مضرب های طبیعی یک عدد
فصل 2 : عددهای اول
مضرب های طبیعی یک عدد
برای نوشتن مضرب های طبیعی یک عدد ، کافی است عدد داده شده را به ترتیب در اعداد طبیعی ضرب کنیم تا مضرب های طبیعی آن بدست بیاید.
مثال
مضرب های طبیعی عددهای زیر را بنویسید.
مضرب های طبیعی 5
مضرب های طبیعی 6
مضرب های طبیعی 5 \( = 1 \times 5\,,\,2 \times 5\,,\,3 \times 5\,,\,4 \times 5\,,\, \cdots = 5\,,\,10\,,\,15\,,\,20\)
مضرب های طبیعی 6\( = 6\,,\,12\,,\,18\,,\,24\,,\,30\,,\,36\,,\, \cdots \)
با توجه به مثال بالا می توان نکته های زیر را نتیجه گرفت:
1 فقط اولین مضرب هر عدد اول ، عددی اول است و بقیه مضرب های آن مرکب هستند؛ مثلا 5 عددی اول است پس اولین مضرب آن یعنی خود 5 ، اول و بقیه مضرب های آن یعنی ...و 20 و 15 و 10 مرکب هستند.
2 همه مضرب های یک عدد مرکب ، مرکب هستند؛ مثلاً 6 عددی مرکب است پس همه مضرب های آن مرکب هستند.
به این ترتیب، اعداد طبیعی به سه بخش تقسیم می شوند:
1 عدد 1
2 عددهای اول
3 عددهای مرکب
مثال
الف عدد 10 چند مضرب دارد؟
بی شمار
ب چند تا از مضرب های آن عدد اول هستند؟
هیچ کدام؛ زیرا خود 10 عددی مرکب است،پس همه مضرب های آن نیز مرکب اند.
پ تنها مضرب اول عدد 23 کدام است؟
خود عدد 23
تعداد شمارنده های یک عدد محدود است اما تعداد مضرب های آن بی شمار!
دو عدد متباین (نسبت به هم اول)
اگر ب.م.م (بزرگترین مقسوم علیه مشترک) دو عدد برابر یک باشد، می گوییم دو عدد نسبت به هم اول هستند؛ به عنوان مثال عدد های 6 و 35 نسبت به هم اول هستند؛ زیرا:
مضرب های طبیعی 5\( = 1\,,\,5\,,\,7\,,\,35\)
مضرب های طبیعی 6\( = 1\,,\,2\,,\,3\,,\,6\)
\( \Rightarrow (35\,,\,6) = 1\)
1 هر دو عدد اول متمایز نسبت به هم اول هستند؛ مانند: \((23\,,\,11) = 1\)
2 هر دو عدد طبیعی متوالی نسبت به هم اول هستند؛ مانند: \((31\,,\,32) = 1\)
3 عدد یک و هر عدد طبیعی بزرگتر از یک نسبت به هم اول هستند؛ مانند: \((25\,,\,1) = 1\)
4 اگر دو عدد طبیعی نسبت به هم اول باشند ، ک.م.م (کوچکترین مضرب مشترک) آنها از حاصل ضرب آن دو عدد بدست می آید؛ مثلا 1 = (3 و 4)؛ آن گاه ک.م.م آن دو برابر است با:
\([4\,,\,3] = 4 \times 3 = 12\)
مثال
الف سه عدد مرکب بنویسید که غیر از 2 و 7 شمارنده اول دیگری نداشته باشند.
چون 2 و 7 هر دو شمارنده های اول این اعداد هستند پس باید آنها را در هم ضرب کنیم و چون غیر از 2 و 7 شمارنده اول دیگری ندارند، پس برای ساخت عدد های بعدی باید به تعداد دلخواه 2 و 7 را در هم ضرب کنیم.
\(\begin{array}{l}2 \times 7 = 14\\\\2 \times 2 \times 7 = 28\\\\2 \times 2 \times 2 \times 7 = 56\\\\2 \times 7 \times 7 = 98\end{array}\)
ب آیا این عددها نسبت به عددی که شمارنده های اول آن 7 و 13 باشند، اول است ؟
خیر؛ زیرا شمارنده مشترک 7 را دارند؛ پس نسبت به هم اول نیستند.
مثال
اگر تعداد عدد های اول کمتر از 35، 11 عدد باشند، تعداد عددهای مرکب کمتر از 35 چند تا است؟ چرا؟
عددهای طبیعی سه بخش می شوند: یک، عدد اول، عدد مرکب. در اینجا از 35 عدد، 11 عدد اول هستند و یکی دیگر از آن 35 عدد، عدد یک است (که نه اول است و نه مرکب). در نتیجه (12 = 11 + 1) 12 عدد از 35 عدد مرکب نیستند؛ پس تعداد عدد های مرکب کمتر از 35:
23 = 12 – 35
مجموع دو عدد اول، 25 است. حاصل ضرب آن دو عدد را بدست آورید.
هرگاه مجموع یا تفاضل دو عدد طبیعی ، عددی فرد باشد یکی از آنها زوج و دیگری فرد بوده است. در اینجا چون ذکر شده مجموع دو عدد اول ،پس می نویسیم: (25 = عدد زوج اول + عدد فرد اول) و چون تنها عدد زوج اول عدد 2 می باشد؛ پس داریم:
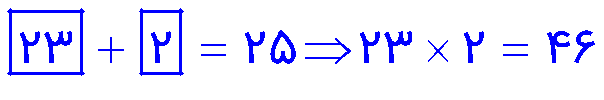
عددهای 15 و 21 دو شمارنده یک عدد هستند. شش شمارنده دیگر این عدد را بنویسید.
\(\left\{ \begin{array}{l}15 = 3 \times 5\\\\21 = 3 \times 7\end{array} \right. \Rightarrow \,5 \times 7 = 35\,\,\,,\,\,\,3 \times 5 \times 7 = 105\)
دیگر شمارنده ها:
105، 35، 7، 5، 3، 1
توجه کنید که یک شمارنده همه عدد ها است و چون در ساختار 15 و 21 عدد های 3 و 5 و 7 وجود دارد پس در واقع در ساختار عدد اصلی هم باید وجود داشته باشند و در نهایت حاصل ضرب این عددها (یعنی 3 و 5 و 7) نیز در ساختار عدد اصلی وجود دارد.
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
یادآوری چند قاعده بخش پذیری
فصل 2 : عددهای اول
یادآوری چند قاعده بخش پذیری
1- بخش پذیری بر 2:
عددی بر 2 بخش پذیر است که رقم یکان آن 0 و 2 و 4 و 6 و 8 باشد. (یا زوج باشد)
2- بخش پذیری بر 3:
عددی بر 3 بخش پذیر است که مجموع ارقامش بر 3 بخش پذیر باشد.
3- بخش پذیری بر 5:
عددی بر 5 بخش پذیر است که رقم یکان آن 0 یا 5 باشد.
غربال
فصل 2 : عددهای اول
روش غربال
برای تعیین عددهای اول از روش غربال استفاده می کنیم. در این روش، در واقع عددهای غیر اول را خط می زنیم تا عددهای اول باقی بمانند. به این ترتیب که:
1) ابتدا عدد یک را خط می زنیم. (زیرا یک نه اول است و نه مرکب)
2) عدد 2، اول است و همه مضرب های آن به جز خود 2، مرکب هستند. پس همه اعداد زوج به غیر از عدد 2 را خط می زنیم.
3) عدد 3، اول است. تمام مضرب های عدد 3 را، به جز خود 3 خط می زنیم.
و به همین ترتیب خط زدن را تا عدد اولی که مربع (توان دوم) آن بین عدد های نوشته شده نباشد، ادامه می دهیم.
دقت کنید
در اینجا اولین مضرب مرکب هر عدد اول که برای اولین بار خط می خورد، توان دوم آن عدد اول است؛ مثلا اولین مضرب مرکب 5 که برای اولین بار خط می خورد، \({5^2} = 25\) می باشد و در نهایت اعداد خط نخورده باقی مانده، اول هستند.
مثال
می خواهیم عدد های اول بین 1 تا 30 را بیابیم.
1 ابتدا عدد یک خط می خورد:
2 عدد 2 اول است پس اولین مضرب مرکب 2 که خط می خورد، مربع 2 یعنی 4 می باشد و بعد از آن می توان گفت بقیه ی مضرب های مرکب 2 را به صورت 2 تا 2 تا بعد از 4 خط می زنیم. (بعنی ... و 8 و 6 و 4)
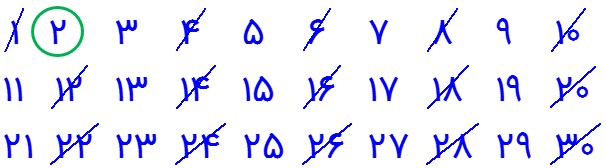
3 عدد 3 اول است و مضرب های مرکب آن که هنوز خط نخورده اند را با شروع از 9 (یعنی مربع عدد 3) به صورت 3 تا 3 تا خط می زنیم.
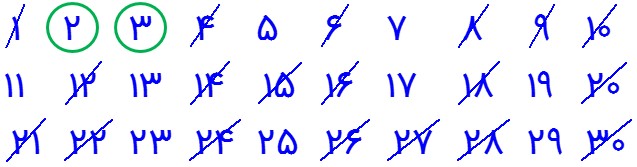
4 خط زدن را تا مربع عدد 5 ، یعنی 25 ادامه می دهیم. زیرا بعد از آن ، مربع عدد 7 را داریم که 49 می شود و چون 49 از 30 بزرگتر است پس کار خط زدن عدد های مرکب تمام می شود و عدد های باقیمانده که دورشان خط کشیده شده، همه اول هستند.
عددهای اول بین 30 تا 50 را با روش غربال بنویسید.
راهنمایی:
دقت کنید در اینجا ابتدای کار ما عدد یک نیست . در نتیجه قطعا اولین مضرب عدد اول 2 هم که خط می خورد عدد 4 نیست. در این سوال ها می توانید از قوانین بخشپذیری برای یافتن اولین مضرب مرکب عدد اول (در اینجا عدد 2) استفاده کنید.
توجه داشته باشید که در این سوال ها هم برای بعضی از عدد های اول ، اولین مضرب مرکب همان توان دوم عدد اول است. در اینجا اولین مضرب 2 که خط می خورد عدد 32 می باشد.
1 مضرب های عدد اول 2 را خط می زنیم. زیرا: \({2^2} = 4 < 49\)
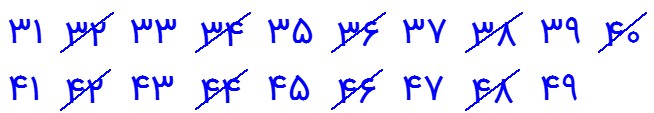
در اینجا اولین مضرب 3 که خط می خورد عدد 33 می باشد.
2 مضرب های عدد اول 3 را خط می زنیم؛ زیرا: \({3^2} = 9 < 49\)
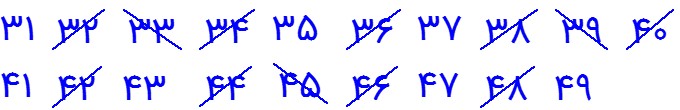
در اینجا اولین مضرب 5 که خط می خورد عدد 35 می باشد.
3 مضرب های عدد اول 5 را خط می زنیم؛ زیرا: \({5^2} = 25 < 49\)
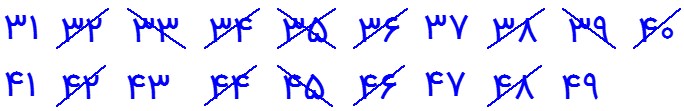
در اینجا اولین مضرب 7 که خط می خورد همان مربع عدد 7 یعنی 49 می باشد و چون مربع عدد اول بعدی یعنی 11، 121 می شود و از 49 بزرگتر است پس کار خط زدن تمام می شود.
4 مضرب های اول 7 را خط می زنیم . زیرا \({7^2} = 49\) و اعداد باقیمانده همان اعداد اول در فاصله 30 تا 50 می باشند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
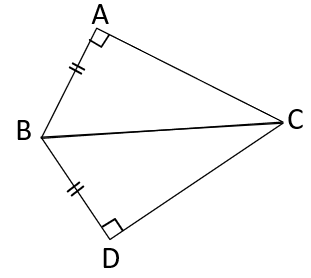
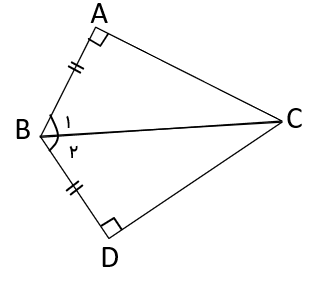
چند ضلعی ها و تقارن
فصل 3 : چندضلعی ها
یادآوری
همانطور که در سال های قبل آموختیم خط ها را می توان به سه دسته تقسیم کرد:
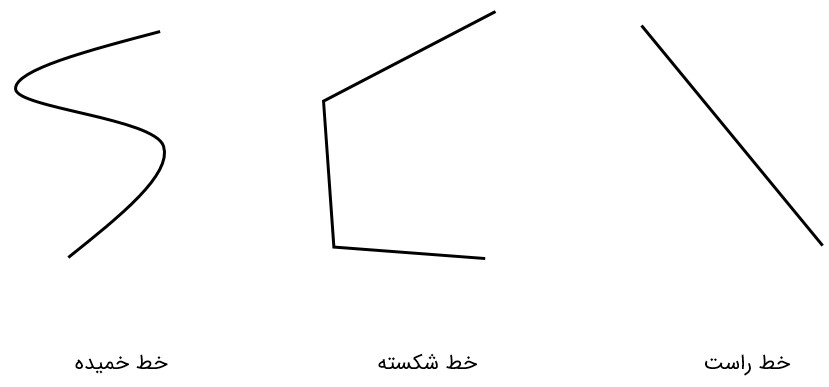
چند ضلعی
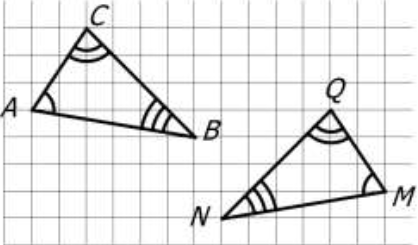
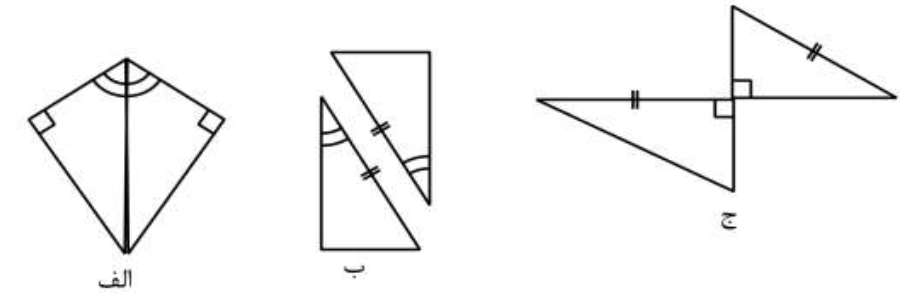
به هر خط شکسته بسته، با این شرط که ضلع ها یکدیگر را قطع نکنند مگر در رأس ها که دو ضلع به هم می رسند چندضلعی می گویند؛ مانند:
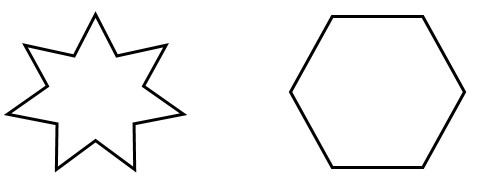
مثال
آیا شکل های زیر هر کدام یک چندضلعی هستند؟ چرا؟
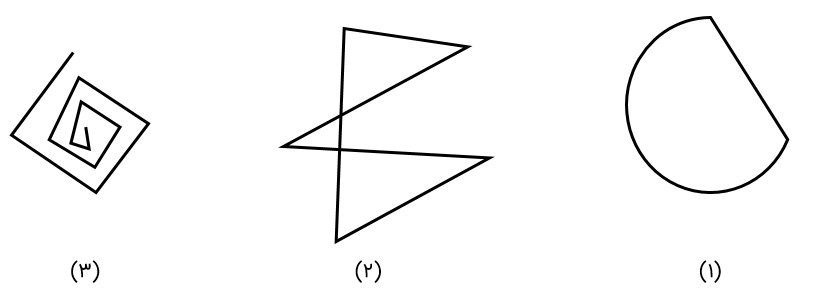
خیر:
شکل (1) چند ضلعی نیست؛ زیرا خط شکسته نیست.
شکل (2) چند ضلعی نیست؛ زیرا ضلع ها در جایی غیر از رأسها یکدیگر را قطع می کنند.
شکل (3) چند ضلعی نیست؛ زیرا خط شکسته بسته نیست.
تهیه کننده: افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
چندضلعی ها
فصل 3 : چندضلعی ها
چندضلعی ها
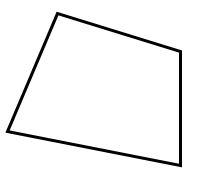
1- چند ضلعی محدب (کوژ):
چندضلعی که تمام زاویه هایش، هرکدام کمتر از \(180^∘\) باشد، چندضلعی محدب یا کوژ نام دارد؛ مانند:
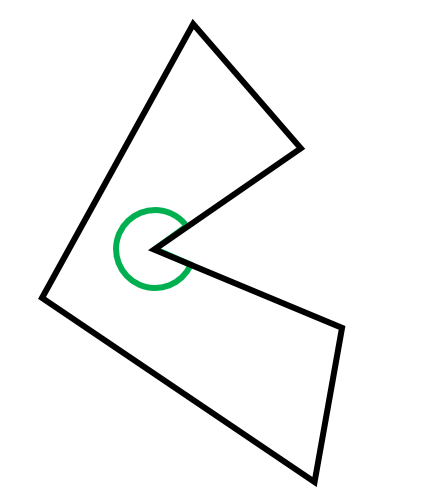
2- چندضلعی مقعر (کاو):
چندضلعی که تمام زاویه هایش، هرکدام بیشتر از \(180^∘\) باشد، چندضلعی مقعر یا کاو نام دارد؛ مانند:
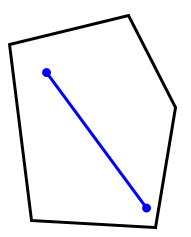
1 در چندضلعی های محدب هر دو نقطۀ دلخواه را بهم وصل کنیم تمام خط ایجاد شده در درون شکل قرار می گیرد؛ مانند:
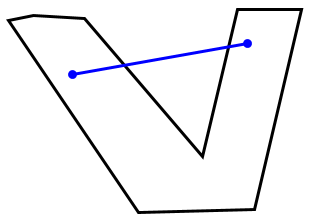
2 اما در چندضلعی های مقعر حداقل دو نقطه وجود دارد که اگر بهم وصل کنیم تمام خط و یا قسمتی از آن در درون شکل قرار نمی گیرد؛ مانند:
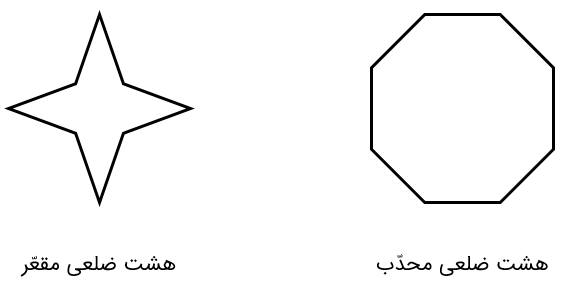
مثال
یک هشت ضلعی محدب و یک هشت ضلعی مقعر رسم کنید.
3- چندضلعی های منتظم:
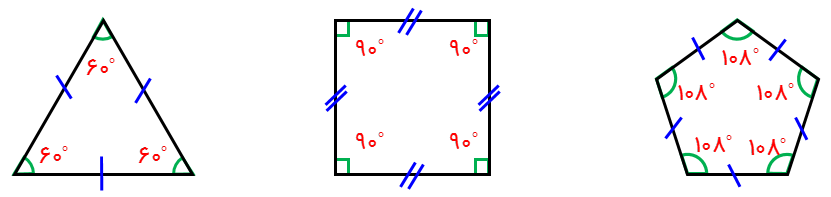
اگر در یک چندضلعی همۀ زاویه ها با هم و همۀ ضلع ها نیز با هم مساوی باشند، چندضلعی منتظم است؛ مانند:
کدام گزینه یک شکل منتظم است؟
الف) لوزی
ب) مثلث متساوی الساقین
ج) مستطیل
د) مثلث متساوی الاضلاع
جواب صحیح گزینه «د» می باشد:
در مثلث متساوی الاضلاع، تمام زوایای داخلی مثلث برابر \(60^∘\) می باشد و اندازه تمام اضلاع آن، با هم برابر هستند.
1 در چندضلعی های منتظم هر چه تعداد ضلع ها بیشتر شود، اندازۀ زاویه ها بزرگتر می شود.
2 در چندضلعی های منتظم هر چه تعداد ضلع ها بیشتر شود، شکل بیشتر به دایره شبیه می شود.
تهیه کننده: افسانه پهلیانی
تقارن
فصل 3 : چندضلعی ها
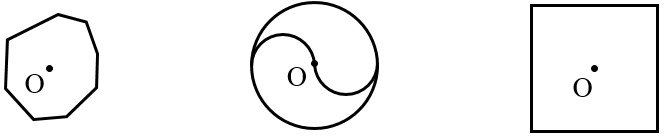
مرکز تقارن
اگر شکلی را حول نقطه ای که درون خود شکل قرار دارد، \({180^ \circ }\) دوران دهید و نتیجۀ دوران روی خودش منطبق شود، آن نقطه مرکز تقارن شکل است. به عنوان مثال به شکل زیر نگاه کنید. ملاحظه می کنید شکل بعد از دوران \({180^ \circ }\) حول نقطه مشخص شده دوباره بر خودش منطبق شده است؛ پس نقطۀ مشخص شده مرکز تقارن است:
اما در شکل زیر ملاحظه می کنید شکل بعد از \({180^ \circ }\) دوران حول نقطۀ مشخص شده دوباره بر خودش منطبق نمی شود. پس نقطۀ مشخص شده مرکز تقارن نیست.
.
روشی دیگر برای تعیین مرکز تقارن
نقاطی را روی شکل تعیین کنید و قرینۀ آن نقاط را نسبت به مرکز مشخص شده بیابید. اگر نقطه ایی وجود داشت که قرینه اش روی شکل قرار نگرفت، نتیجه بگیرید مرکز تقارن نیست.
یادآوری
برای بدست آوردن قرینۀ هر نقطه از شکل، ابتدا آن را به نقطۀ مشخص شده درون شکل وصل می کنید و به اندازۀ خودش و در همان راستا امتداد می دهید؛ مثلاً:
با استفاده از همین روش تعیین کنید در کدامیک از شکل های زیر نقطۀ O مرکز تقارن است.
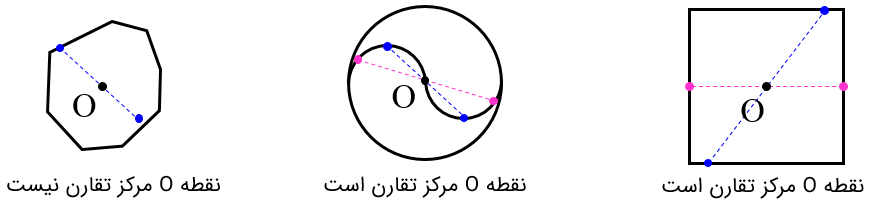
1 به طور کلی در چندضلعی های منتظم که تعداد ضلع ها زوج باشد مرکز تقارن وجود دارد؛ مانند مربع و ده ضلعی منتظم.
2 به طور کلی در چندضلعی های منتظم که تعداد ضلعها فرد باشد مرکز تقارن وجود ندارد؛ مانند پنج ضلعی منتظم و هفت ضلعی منتظم.
مثال
کدام یک از شکل های زیر مرکز تقارن دارد؟
الف نیم دایره
ب مثلث متساوی الاضلاع
ج نه ضلعی منتظم
د متوازی الاضلاع
پاسخ صحیح گزینه «د» می باشد:
متوازی الاضلاع دارای مرکز تقارن می باشد.
محور تقارن
خطی که شکل را به دو قسمت مساوی تقسیم می کند به طوری که اگر شکل را از روی آن خط تا بزنیم دو قسمت بر هم منطبق می شوند، و هر قسمت همانند آینه ای است برای قسمت دیگر؛ مانند:
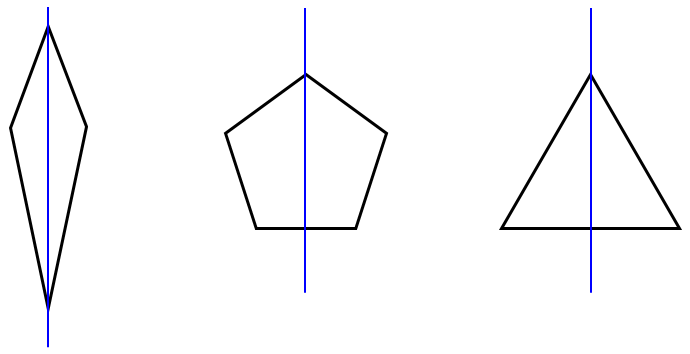
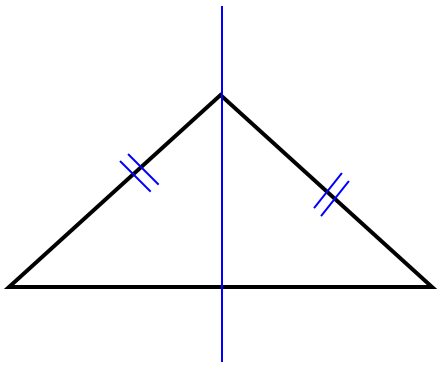
1 ممکن است شکلی مرکز تقارن نداشته باشد ولی محور تقارن داشته باشد؛ مانند مثلث متساوی الساقین:
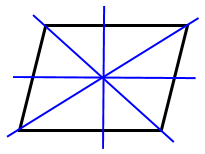
2 ممکن است شکلی مرکز تقارن داشته باشد ولی محور تقارن نداشته باشد؛ مانند متوازی الاضلاع:
مثال
هفت ضلعی منتظم هفت محور تقارن دارد (مرکز تقارن ندارد) و ده ضلعی منتظم ده محور تقارن دارد (مرکز تقارن دارد)
نسبت تعداد محور تقارن یک هشتضلعی منتظم به یک ششضلعی منتظم برابر است با ............ .
تهیه کننده:افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
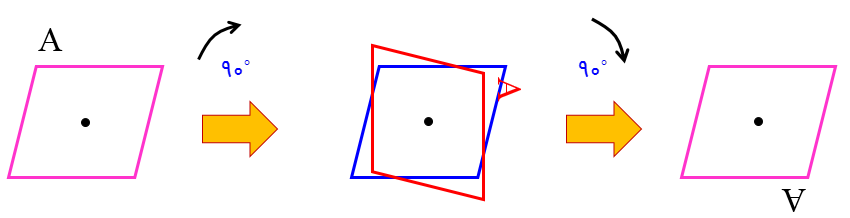
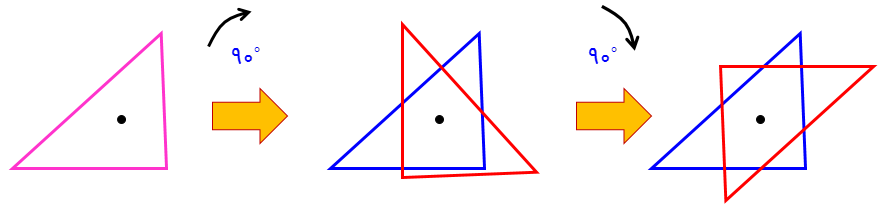
دوران
فصل 3 : چندضلعی ها
دوران
اگر شکلی را روی صفحه حول یک نقطۀ ثابت (مرکز دوران) با زاویهای مشخص بچرخانیم تصویر حاصل دوران یافتۀ شکل می باشد.
1 در دوران \({180^ \circ }\) و \({360^ \circ }\) نیاز به مشخص کردن جهت دوران نیست ولی اگر زاویۀ دوران \({180^ \circ }\) و \({360^ \circ }\) نباشد باید جهت دوران مشخص شود.
2 در هر دوران تصویر بدست آمده (دوران یافته) هم اندازه و همنهشت با شکل است:
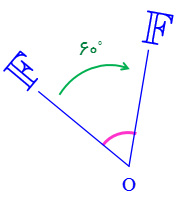
دوران 60 درجه در جهت حرکت عقربه های ساعت.
تقارن چرخشی (دورانی) در چندضلعی های منتظم
اگر سه ضلعی منتظم (مثلث متساوی الاضلاع) را حول مرکز O با زاویۀ دوران \({120^ \circ }\) دوران دهیم بر خودش منطبق می شود.
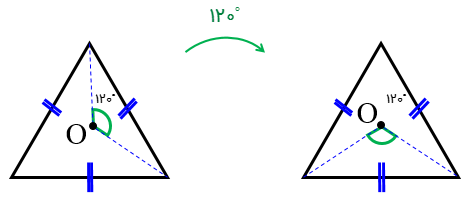
حداقل زاویۀ دوران در تقارن چرخشیِ چندضلعی های منتظم را می توان از دستور زیر بدست آورد:
\((0 < \alpha \le {360^ \circ })\)
\(\alpha = {360^ \circ } \div \)تعداد ضلع
سایر دورانها مضرب های \(\alpha \) هستند.
مثال
سه ضلعی منتظم (مثلث متساوی الاضلاع) با چه دورانه ایی حول نقطۀ O بر خودش منطبق می شود؟
\({360^ \circ } \div 3 = {120^ \circ } \Rightarrow \alpha = {120^ \circ }\,,\,{240^ \circ }\,,\,{360^ \circ }\)
در کدام یک از گزینه های زیر چندضلعی منتظم با دوران 90 درجه حول نقطۀ مشخص شده در جهت حرکت عقربه های ساعت بر خودش منطبق می شود؟
جواب صحیح گزینه «الف» می باشد:
\({360^ \circ } \div 8 = {45^ \circ } \Rightarrow \alpha = {45^ \circ }\,,\,{90^ \circ }\,,\,{135^ \circ }\)
هشت ضلعی منتظم با دوران های \({45^ \circ }\,,\,{90^ \circ }\,,\,{135^ \circ }\,,\,{180^ \circ }\,,\,{225^ \circ }\,,\,{270^ \circ }\,,\,{315^ \circ }\,,\,{360^ \circ }\) حول نقطۀ مشخص شده بر خودش منطبق می شود.
تهیه کننده:افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
توازی و تعامد
فصل 3 : چندضلعی ها
توازی و تعامد
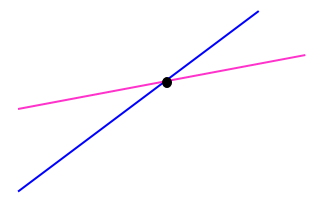
دو خط متمایز در صفحه نسبت به هم دو حالت دارند:
1) دو خط موازی هستند و هیچ نقطه مشترکی ندارند:
2) دو خط متقاطع اند و یک نقطه مشترک دارند:
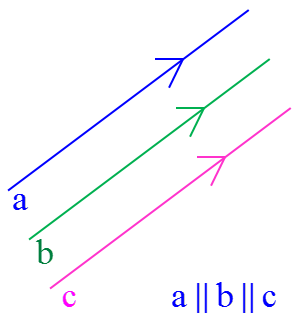
1 برای اینکه خطوط موازی را نشان دهیم روی آنها علامت های یکسان (<) یا (<<) یا (<<<) یا ... قرار می دهیم و بین اسامی آنها از علامت (||) استفاده می کنیم:
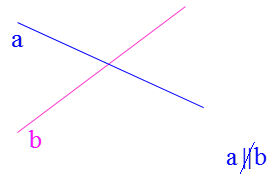
2 اگر خطوط داده شده موازی نباشند و متقاطع باشند بین اسامی آنها از علامت \({\parallel } \) استفاده می کنیم:
3 اگر خطوط متقاطع بر هم عمود باشند بین اسامی آنها از علامت \( \bot \) استفاده می کنیم:
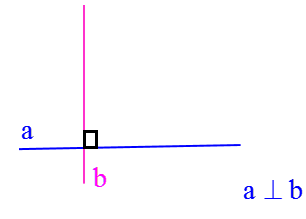
دو خط موازی
در دورۀ ابتدایی آموختید که دو خط موازی هیچگاه یکدیگر را قطع نمیکنند ممکن است این پرسش در ذهن شما بوجود بیاید که :برای تشخیص موازی بودن دو خط باید تا کجا آن دو را ادامه دهیم که مطمئن شویم موازی هستند؟ و اما در ادامه روشی را معرفی میکنیم که برای تشخیص موازی بودن دو خط مفید است.
تعریف دیگری برای دو خط موازی
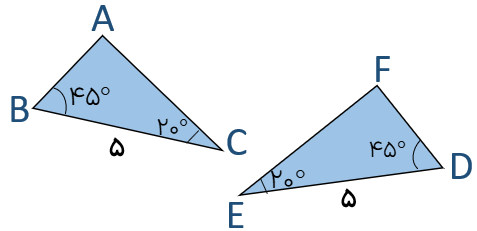
هرگاه خطی مانند d، دو خط a و b را قطع کند و زاویه های مساوی ایجاد کند، نتیجه می گیریم دو خط a و b موازی هستند.
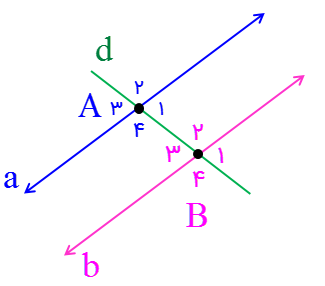
\({\hat A_1} = {\hat A_3} = {\hat B_1} = {\hat B_3}\)(زاویه های تند مساویند)
\({\hat A_2} = {\hat A_4} = {\hat B_2} = {\hat B_4}\)(زاویه های باز مساویند)
\( \Rightarrow a\parallel b\)
به عنوان مثال:
در شکل مقابل خط d دو خط a و b را طوری قطع کرده که زاویه های مساوی ایجاد کرده است پس دو خط a و b موازیند:
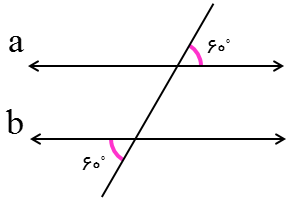
زاویه های تند\( = {60^ \circ }\)
زاویه های باز\( = {120^ \circ }\)
\( \Rightarrow a\parallel b\)
با توجه به شکل مقابل آیا دو خط a و b موازیند؟
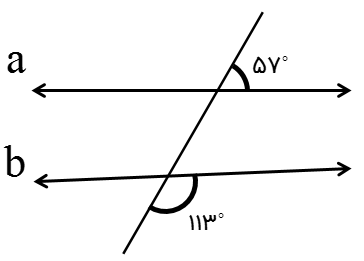
خیر؛ زیرا زاویه های تند با هم مساوی نیستند و زاویه های باز نیز با هم مساوی نیستند.
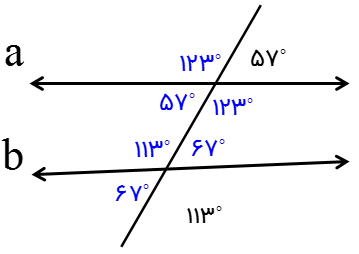
در نتیجه: \( \Rightarrow a{\parallel }b\)
اگر خط مورّبی دو خط موازی را قطع کند با آنها زاویه های مساوی می سازد.
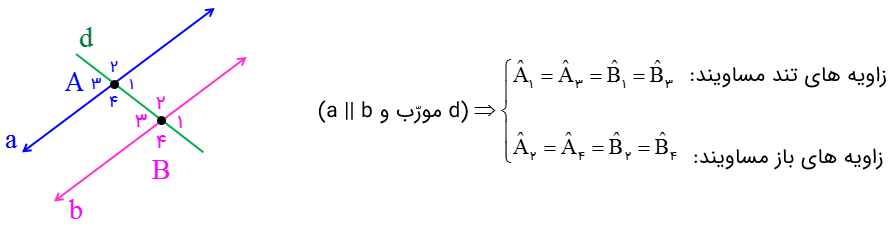
و هر زاویۀ باز با هر زاویۀ تند مکمل است:
\({\hat A_1} + {\hat B_3} = {180^ \circ }\)
دو خط a و b در شکل مقابل موازیند. اندازۀ زاویۀ خواسته شده را بدست آورید.
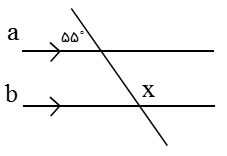
زاویۀ x زاویه ای باز است و مکمل \({55^ \circ }\) ؛ بنابراین: \(x = {180^ \circ } - {55^ \circ } + {125^ \circ }\)
با توجه به دو خط موازی اندازۀ زاویه های خواسته شده را بدست آورید
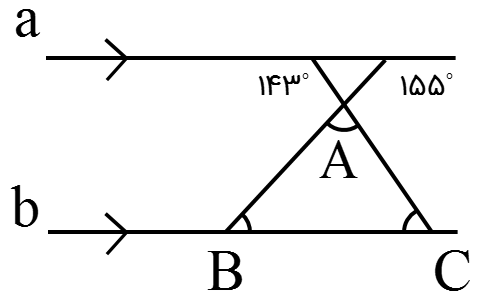
\(\hat A = \,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\hat B = \,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\hat C = \)
اگر شکل را به دو قسمت زیر تقسیم کنیم:
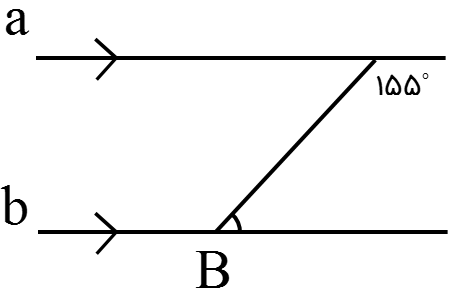
در این قسمت \(\hat B\) مکمل زاویه \({155^ \circ }\) است:
\(\hat B = {180^ \circ } - {155^ \circ } = {25^ \circ }\)
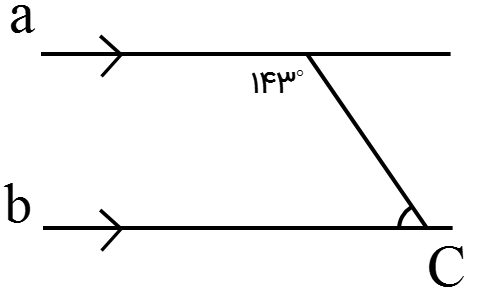
در این قسمت \(\hat C\) مکمل زاویه \({143^ \circ }\) است:
\(\hat C = {180^ \circ } - {143^ \circ } = {37^ \circ }\)
برای بدست آوردن \(\hat A\) با توجه به اینکه مجموع زوایای داخلی هر مثلث \({180^ \circ }\) است، داریم:
\(\hat A = {180^ \circ } - (\hat B + \hat C) = {180^ \circ } - ({25^ \circ } + {37^ \circ }) = {180^ \circ } - {62^ \circ } = {118^ \circ }\)
شکل مقابل با توجه به موازی بودن دو خط مقدار x را تعیین کنید.
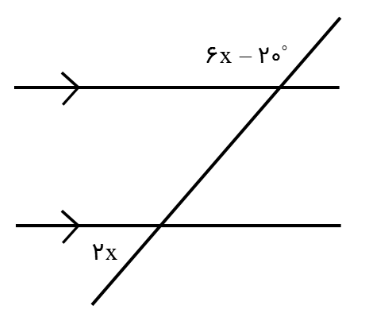
2x اندازۀ زاویۀ تند و \(6x - {20^ \circ }\) اندازۀ باز است دو زاویه مکمل یکدیگر هستند یعنی:
\(6x - {20^ \circ } + 2x = {180^ \circ }\)
سپس با معادله x را تعیین می کنیم:
\(\begin{array}{l}8x - {20^ \circ } = {180^ \circ } \Rightarrow 8x = {180^ \circ } + {20^ \circ } = {200^ \circ }\\\\ \Rightarrow x = \frac{{{{200}^ \circ }}}{8} \Rightarrow x = {25^ \circ }\end{array}\)
نکاتی در مورد خطوط موازی:
1 دو خط عمود بر یک خط، با هم موازیند.
\(\left\{ \begin{array}{l}a \bot d\\\\b \bot d\end{array} \right. \Rightarrow a\parallel b\)
2 دو خط موازی با یک خط، با هم موازیند.
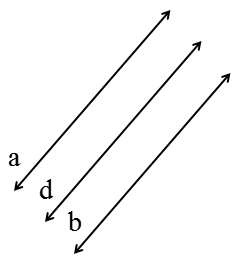
\(\left\{ \begin{array}{l}a\parallel d\\\\b\parallel d\end{array} \right. \Rightarrow a\parallel b\)
3 اگر خطّی بر یکی از دو خطّ موازی عمود باشد، بر دیگری نیز عمود خواهد بود.
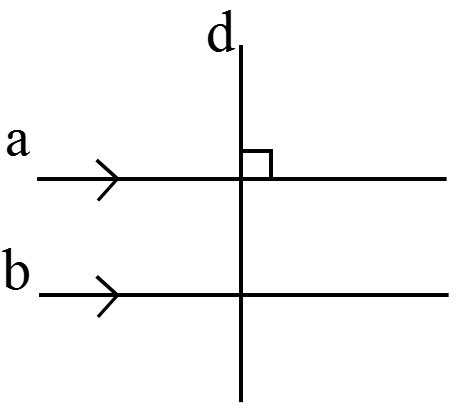
\(\left\{ \begin{array}{l}a \bot d\\\\a\parallel b\end{array} \right. \Rightarrow d \bot b\)
4 در متوازی الاضلاع، ضلع های رو به رو با هم موازیند با کمک روابط موجود بین خطوط موازی و مورّب که در این درس آموختید، می توان نتیجه گرفت در هر متوازی الاضلاع زاویه های رو به رو با هم برابرند و زاویه های مجاور مکمل اند.
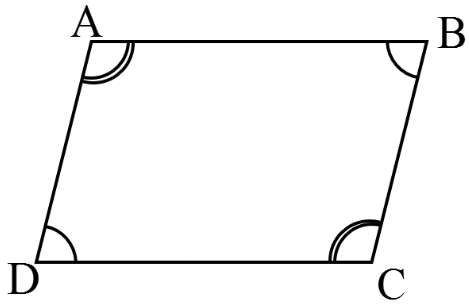
\(\begin{array}{l}\left\{ \begin{array}{l}\hat A = \hat C\\\\\hat D = \hat B\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\hat A + \hat B = {180^ \circ }\\\\\hat B + \hat C = {180^ \circ }\end{array} \right.\,\,\,\,\,\,\left\{ \begin{array}{l}\hat C + \hat D = {180^ \circ }\\\\\hat D + \hat A = {180^ \circ }\end{array} \right.\\\end{array}\)
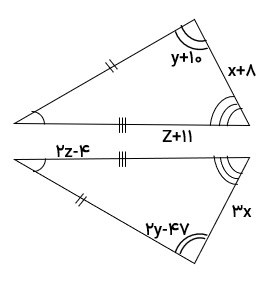
با توجه به اینکه شکل مقابل متوازی الاضلاع ست، مقدار x را تعیین کنید.
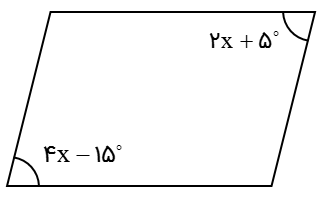
در متوازی الاضلاع دو زاویه رو به رو با هم مساوی هستند.
\(2x + {5^ \circ } = 4x - {15^ \circ }\)
به کمک حل معادله، مقدار x را تعیین می کنیم:
\(\begin{array}{l}2x + {5^ \circ } = 4x - {15^ \circ } \Rightarrow 4x - 2x = {5^ \circ } + {15^ \circ }\\\\ \Rightarrow 2x = {20^ \circ } \Rightarrow x = \frac{{{{20}^ \circ }}}{2} \Rightarrow x = {10^ \circ }\end{array}\)
1 هر جا خطوط موازی را به صورت حرف Z و یا حرف N دیدیم و یا برعکس آنها، زاویه های تند آنها با هم مساویند؛ مانند:
اندازۀ زاویه x چند درجه است؟
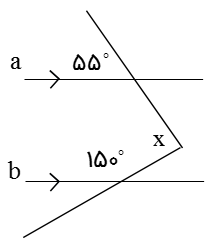
1) \({55^ \circ }\) 2) \({30^ \circ }\) 3) \({95^ \circ }\) 4) \({85^ \circ }\)
پاسخ صحیح گزینه 4 می باشد:
می توان با رسم خطی موازی دو خط شکل را به صورت مقابل تقسیم کنیم:
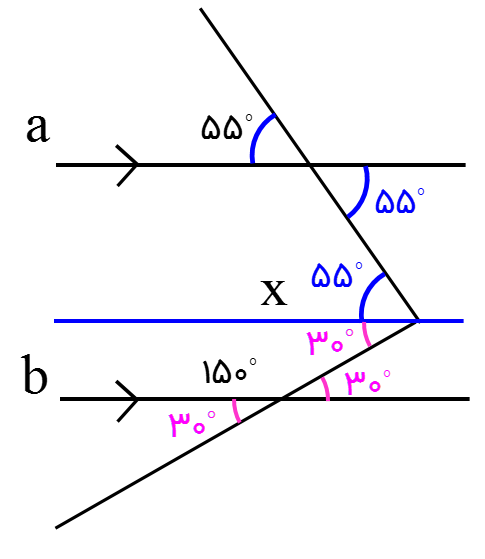
\(x = {55^ \circ } + {30^ \circ } = {85^ \circ }\)
تهیه کننده: افسانه پهلیانی
متوازی الاضلاع
فصل 3 : چندضلعی ها
متوازی الاضلاع
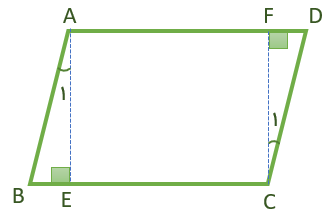
متوازی الاضلاع چهارضلعی است که اضلاع رو به رو دو به دو موازی باشند.
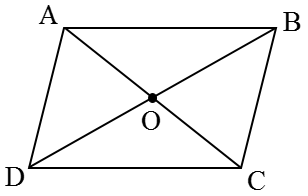
با استفاده از کاغذ پوستی و دوران \({180^ \circ }\) حول مرکز تقارنش (نقطۀ O) مشاهده می کنید که اضلاع رو به رو، روی هم قرار می گیرند (پس با هم برابرند) و زاویه های رو به رو نیز روی هم قرار می گیرند (پس با هم برابرند). با استفاده از دوران و انطباق میتوان ویژگی های متوازی الاضلاع را به صورت زیر نوشت:
1) در هر متوازی الاضلاع، اضلاع رو به رو با هم مساویند:
AB=DC , AD=BC
2) در هر متوازی الاضلاع، زاویه های رو به رو با هم مساویند:
\(\hat A = \hat C\,\,\,,\,\,\,\hat B = \hat D\)
3) در هر متوازی الاضلاع، زاویه های مجاور به یک ضلع مکمل ند:
\(\begin{array}{l}\hat A + \hat B = {180^ \circ }\,\,\,,\,\,\,\hat B + \hat C = {180^ \circ }\\\\\hat C + \hat D = {180^ \circ }\,\,\,,\,\,\,\hat D + \hat A = {180^ \circ }\end{array}\)
4) در هر متوازی الاضلاع، قطرها یکدیگر را نصف می کنند:
AO=OC , BO=OD
5) در هر متوازی الاضلاع، محل برخورد قطرها، مرکز تقارن متوازی الاضلاع است (نقطۀ O)
متوازی الاضلاع، محور تقارن ندارد.
مثال
با توجه به متوازی الاضلاع مقابل مقادیر خواسته شده را بدست آورید.
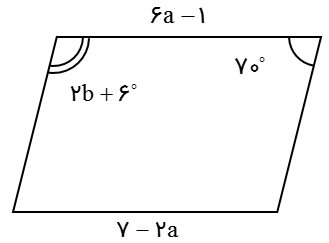
a=… b=…
می دانیم در متوازی الاضلاع، ضلع های رو به رو با هم برابرند. پس 6a-1=7-2a. به کمک حل معادله مقدار a را تعیین می کنیم:
\(6a + 2a = 7 + 1 \Rightarrow 8a = 8 \Rightarrow a = \frac{8}{8} \Rightarrow a = 1\)
می دانیم در متوازی الاضلاع،زاویه های مجاور به یک ضلع مکمل ند. پس \(2b + {6^ \circ } + {70^ \circ } = {180^ \circ }\). به کمک حل معادله مقدار b را تعیین می کنیم:
\(2b = {180^ \circ } - {76^ \circ } = {104^ \circ } \Rightarrow b = \frac{{{{104}^ \circ }}}{2} \Rightarrow b = {52^ \circ }\)
\(2b + {6^ \circ } + {70^ \circ } = {180^ \circ }\)
تهیه کننده : افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مستطیل و لوزی
فصل 3 : چندضلعی ها
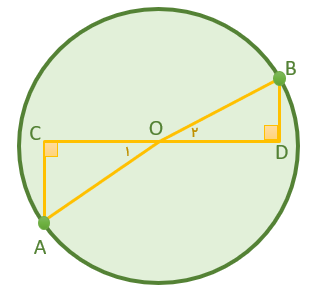
مستطیل
اگر در متوازی الاضلاع، زاویه ها قائمه \(({90^ \circ })\) باشند، مستطیل بوجود می آید. بنابراین مستطیل، متوازی الاضلاعی است که زاویه های قائمه دارد.
اگر مستطیلی را روی یکی از خط های تقارنش و سپس روی خط تقارن دیگرش تا کنید، می توان ویژگی های مستطیل را به صورت زیر نوشت:
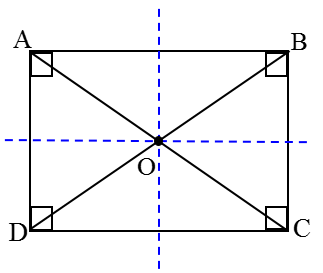
1) در هر مستطیل، همۀ زاویه ها با هم برابرند:
\(\hat A = \hat B = \hat C = \hat D = {90^ \circ }\)
2) در هر مستطیل، ضلع های رو به رو با هم برابرند:
AB=DC , AD=BC
3) در هر مستطیل، قطرها با هم برابرند:
AC=BD
4) در هر مستطیل، قطرها یکدیگر را نصف می کنند:
OA=OB=OC=OD
هر مستطیل دو محور تقارن دارد:
1 خطی که از وسط طول ها می گذرد.
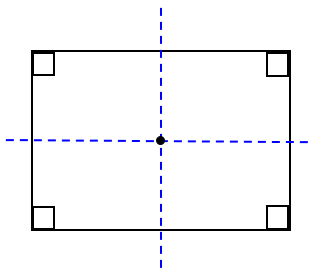
2 خطی که از وسط عرض ها می گذرد.
1 قطرها در مستطیل محور تقارن نیستند.
2 در مستطیل قطرها بر هم عمود نیستند.
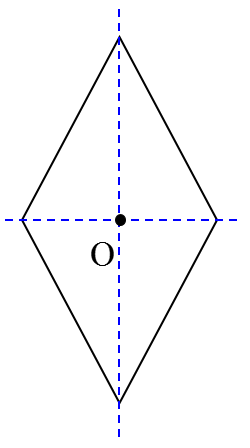
لوزی
اگر در متوازی الاضلاع، همۀ ضلع ها برابر باشند. لوزی به وجود می آید. بنابراین لوزی، متوازی الاضلاعی است که ضلع های برابر دارد:
\(\overline {AB} = \overline {BC} = \overline {CD} = \overline {DA} \)
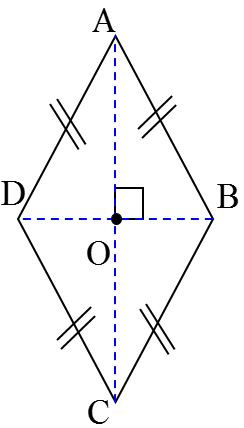
با توجه به اینکه لوزی نوعی متوازی الاضلاع است، علاوه بر همۀ ویژگی های متوازی الاضلاع، ویژگی دیگری نیز دارد:
«در هر لوزی قطرها بر هم عمودند.» یعنی:
\(\overline {AC} \bot \overline {BD} \)
در هر لوزی قطرها محور تقارن هستند و محل برخورد قطرها، مرکز تقارن (نقطۀ O) لوزی است.
تهیه کننده:افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
مربع و ذوزنقه
فصل 3 : چندضلعی ها
مربع
اگر در متوازی الاضلاع، همه ضلع ها هم اندازه و همه زاویه ها قائمه باشند، مربع به وجود می آید. بنابراین مربع، متوازی الاضلاعی است که هم ضلع های مساوی و هم زاویه های قائمه دارد.
\(\begin{array}{l}\overline {AB} = \overline {BC} = \overline {CD} = \overline {DA} \\\\\hat A = \hat B = \hat C = \hat D = {90^ \circ }\end{array}\)
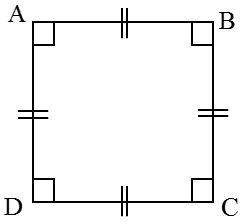
در مربع تمام ویژگی های یک متوازی الاضلاع وجود دارد علاوه بر همۀ ویژگی های متوازی الاضلاع، ویژگی های زیر را هم دارد:
1) در هر مربع قطرها با هم برابرند: AC=BD
2) در هر مربع قطرها بر هم عمودند: \(AC \bot BD\)
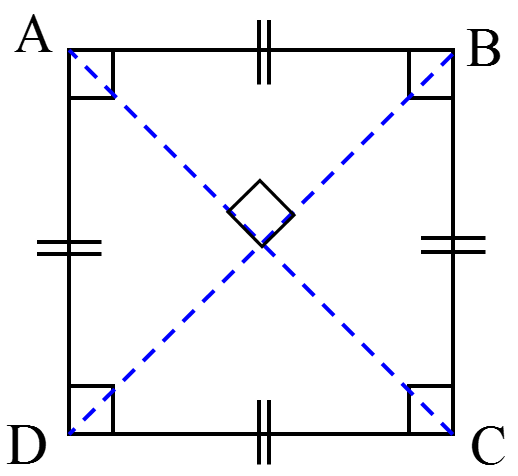
1 هر مربع 4 محور تقارن دارد:
الف دو قطر
ب خطوطی که از وسط هر دو ضلع رو به رو می گذرند.
محل برخورد خط های تقارن، مرکز تقارن (نقطۀ O) مربع است.
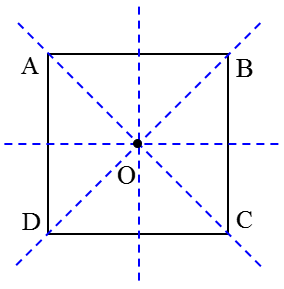
2 هر مربع هم نوعی متوازی الاضلاع، هم نوعی لوزی و هم نوعی مستطیل است. زیرا ویژگی های متوازی الاضلاع، لوزی و مستطیل را دارد.
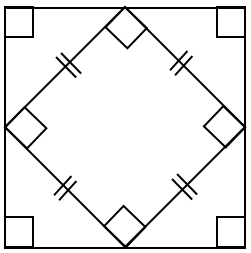
3 اگر وسط های اضلاع یک مربع را به صورت متوالی به هم وصل کنیم شکل بوجود آمده باز هم مربع خواهد بود (با استفاده از خط های تقارن در مربع و تا زدن مربع روی این خطوط می توان به درستی این مطلب پی برد).
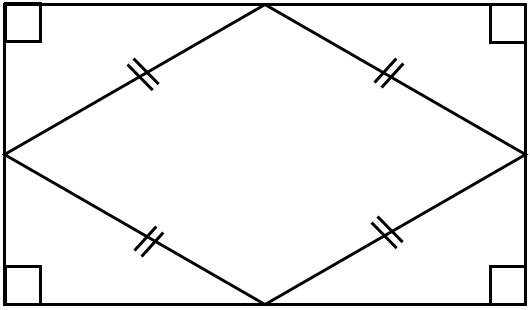
4 اگر وسط های اضلاع یک مستطیل را به صورت متوالی به هم وصل کنیم شکل بوجود آمده یک لوزی خواهد بود (با استفاده از خط های تقارن در مستطیل و تا زدن مستطیل روی این خطوط می توان به درستی این مطلب پی برد).
5 اگر وسط های اضلاع یک متوازی الاضلاع را به صورت متوالی به هم وصل کنیم شکل بوجود آمده، یک متوازی الاضلاع خواهد بود.
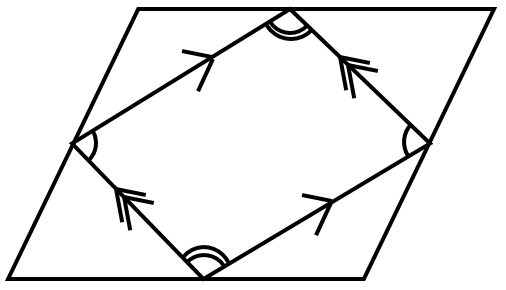
6 اگر وسط های اضلاع یک لوزی را به صورت متوالی به هم وصل کنیم شکل بوجود آمده، یک مستطیل خواهد بود.
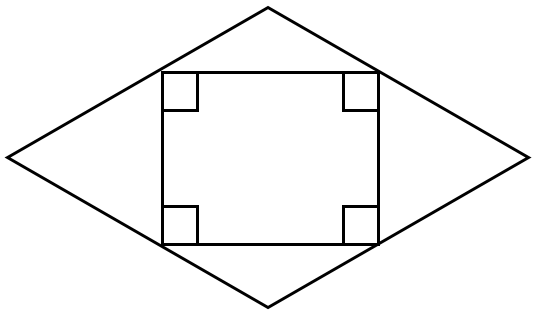
مثال
در شکل مقابل، ABCD مستطیل و DCEF متوازی الاضلاع است. مقدار زاویۀ \(\hat x\) چند درجه است؟
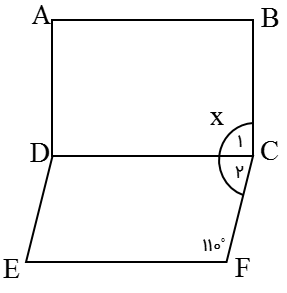
\(\left. \begin{array}{l}\hat x = {{\hat C}_1} + {{\hat C}_2}\\\\{{\hat C}_1} = {90^ \circ }\\\\{{\hat C}_2} + {110^ \circ } = {180^ \circ } \Rightarrow {{\hat C}_2} = {70^ \circ }\end{array} \right\} \Rightarrow \hat x = {90^ \circ } + {70^ \circ } = {160^ \circ }\)
جاهای خالی را با عبارت مناسب پر کنید.
1 اگر وسط های اضلاع یک مستطیل را به طور متوالی به هم وصل کنیم، شکل حاصل ................ خواهد بود.
لوزی
2 در متوازی الاضلاع، محل برخورد قطرها، .................... شکل است.
مرکز تقارن
3 لوزی که دو قطر مساوی دارد، ..................... نام دارد.
مربع
4 متوازی الاضلاعی که یک زاویۀ قائمه دارد ................... نام دارد.
مستطیل
ذوزنقه
چهارضلعی که فقط دو ضلع موازی دارد، ذوزنقه نام دارد (AB||DC).
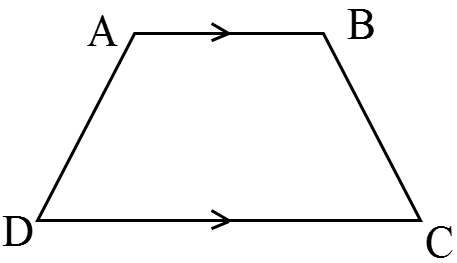
به دو ضلع موازی قاعده و به دو ضلع دیگر که با هم موازی نیستند، ساق می گویند.
در ذوزنقه زاویه های رو به رو با هم مساوی نیستند و قطرها یکدیگر را نصف نمی کنند.
1 در هر ذوزنقه دو زاویۀ مجاور به هر ساق (که با یک ضلع مورّب در ارتباط هستند) مکملند:
\(\hat A + \hat D = {180^ \circ }\,\,\,,\,\,\,\hat B + \hat C = {180^ \circ }\)
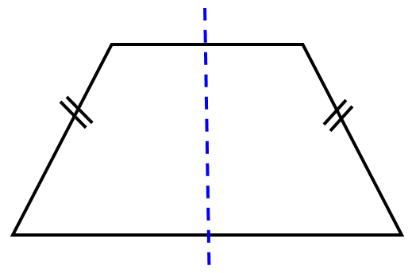
2 اگر در ذوزنقه دو ساق مساوی باشند، ذوزنقه متساوی الساقین خواهد بود.
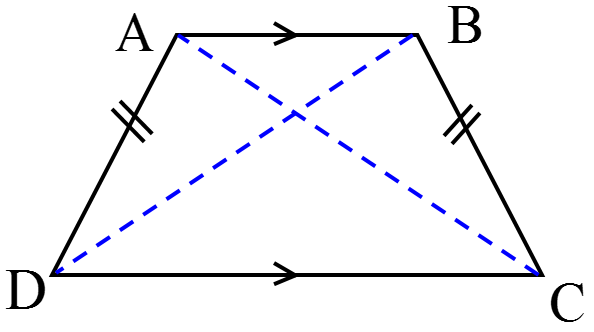
پس دو زاویۀ مجاور به هر قاعده با هم برابرند:
\(\overline {AD} = \overline {BC} \,\,\,,\,\,\,\hat A = \hat B\,\,\,,\,\,\,\hat D = \hat C\)
و دو قطر نیز با هم برابرند:
AC=BD
3 ذوزنقه متساوی الساقین یک خط تقارن دارد:
4 اگر در ذوزنقه یکی از ساق ها بر دو قاعده عمود باشد، ذوزنقه قائم الزاویه خواهد بود:
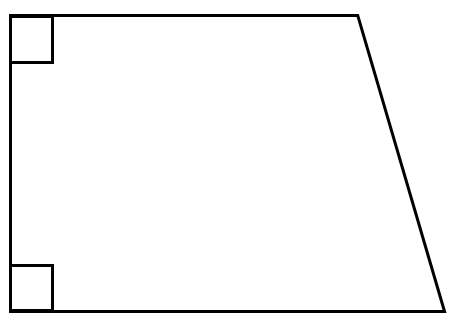
تهیه کننده:افسانه پهلیانی
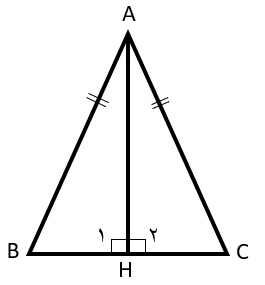
زاویه های داخلی
فصل 3 : چندضلعی ها
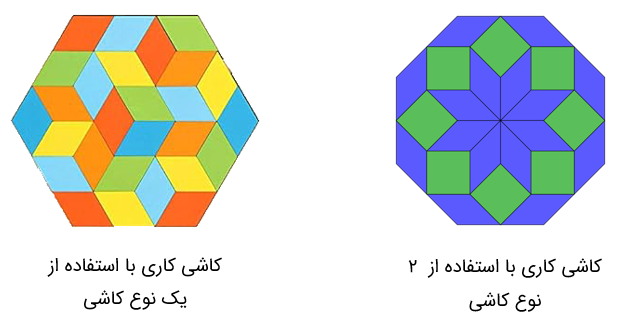
کاشی کاری
گاهی برای پوشاندن یک سطح از یک یا چند نوع کاشی استفاده می کنند به صورتی که کاشی ها روی هم قرار نگیرند و نیز بین آنها فضای خالی نباشد. مانند شکل های زیر:
مثال
به شکل زیر توجه کنید. چرا کاشیکاری با یک نوع کاشی انجام نمی شود؟
زیرا بین کاشی ها فضای خالی وجود دارد.
سطح زیر با مثلث هایی همنهشت با مثلث ABC کاشی کاری شده است.
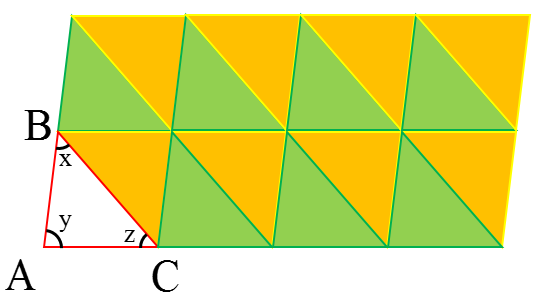
مثلث سبز انتقال یافته مثلث ABC است.
مثلث نارنجی دوران یافته مثلث ABC است.
اگر سه مثلث همنهشت را دوباره رسم کنیم:
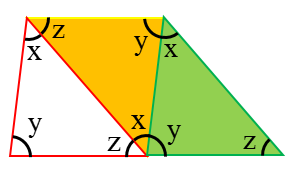
ملاحظه می کنید که سه زاویۀ x، y و z که زاویه های یک مثلث هستند در کنار هم تشکیل زاویۀ نیم صفحه را می دهند، پس:
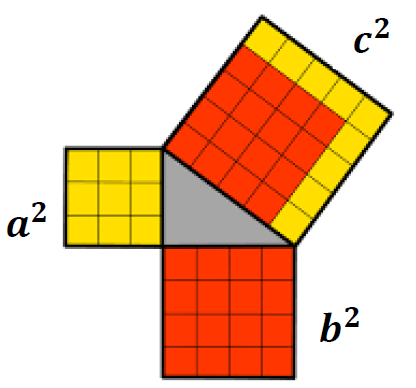
مجموع زاویه های داخلی یک مثلث \({180^ \circ }\) است.
\(\hat A + \hat B + \hat C = {180^ \circ }\)
مجموع زاویه های داخلی یک چندضلعی
منظور از زاویه های داخلی یک چندضلعی، زاویه هایی است که درون چندضلعی قرار دارد و ضلع های زاویه، ضلع های چندضلعی است. برای محاسبه مجموع زاویه های داخلی چندضلعی با رسم تعدادی از قطرهای چندضلعی درون آن تعدادی مثلث ایجاد می کنیم و با توجه به اینکه: «مجموع زاویه های هر مثلث \({180^ \circ }\) است.» مجموع زاویه های داخلی چندضلعی را به دست می آوریم:
\(3 \times {180^ \circ } = {540^ \circ }\)
دقت کنید قطرهایی رسم کنید که یکدیگر را قطع نکنند (به جز در رأس). برای رسم قطرها یک رأس را در نظر می گیریم و به رأس های مقابل وصل می کنیم. با دقت در شکل بالا متوجه می شوید که تعداد مثلث های ایجاد شده در هر چندضلعی 2 تا از تعداد ضلع ها کمتر است. مثلاً مجموع زاویه های داخلی یک شش ضلعی برابر است با:
\((6 - 2) \times {180^ \circ } = 4 \times {180^ \circ } = {720^ \circ }\)
برای محاسبه مجموع زاویه های داخلی چندضلعی از رابطۀ زیر استفاده می کنیم:
180 × (2 – تعداد ضلع ها) = 180 × تعداد مثلث ها = مجموع زاویه های داخلی هر چند ضلعی
شکل مقابل مقدار a را بدست آورید.
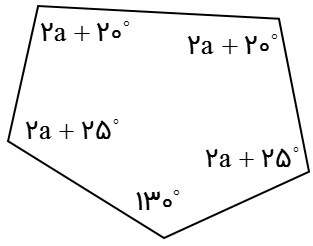
540 = 180 × 3 = مجموع زاویه های داخلی 5 ضلعی
\(\begin{array}{l}2a + {20^ \circ } + 2a + {20^ \circ } + 2a + {25^ \circ } + 2a + {25^ \circ } + {130^ \circ } = {540^ \circ }\\\\ \Rightarrow 8a + {220^ \circ } = {540^ \circ } \Rightarrow 8a = {540^ \circ } - {220^ \circ } = {320^ \circ }\\\\ \Rightarrow a = \frac{{{{320}^ \circ }}}{8} = {40^ \circ }\end{array}\)
محاسبۀ اندازۀ هر زاویۀ داخلی یک چندضلعی منتظم
ابتدا مجموع زاویه های داخلی چندضلعی منتظم را بدست می آوریم و چون در شکل های منتظم زاویه ها با هم برابرند، مجموع زاویه های داخلی را بر تعداد زاویه ها تقسیم می کنیم تا اندازۀ هر زاویه بدست آید.
مثال
اندازۀ هر زاویۀ داخلی هشت ضلعی منتظم را بدست آورید.
1080 = 180 × (2 – 8) = مجموع زاویه های داخلی 8 ضلعی منتظم
135 = 8 ÷ 1080 = اندازه هر زاویه داخلی هشت ضلعی منتظم
اندازۀ هر زاویۀ داخلی n ضلعی منتظم برابر است با \(\frac{{(n - 2) \times {{180}^ \circ }}}{n}\)
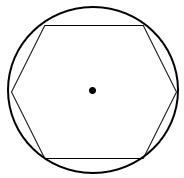
آیا با کاشی هایی به شکل شش ضلعی منتظم می توان به تنهایی کاشی کاری کرد؟
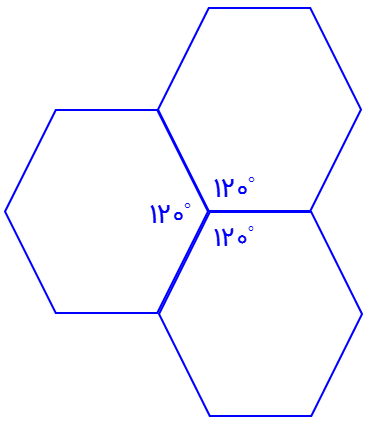
بله؛ در کاشی کاری با شش ضلعی منتظم به تنهایی، هیچ فضای خالی ایجاد نمی شود. ابتدا اندازۀ هر زاویۀ داخلی شش ضلعی منتظم را محاسبه می کنیم. شش ضلعی های منتظم وقتی کنار هم قرار می گیرند در هر گوشه \({120^ \circ }\)، زاویه دارند:
\(\frac{{(6 - 2) \times {{180}^ \circ }}}{6} = \frac{{4 \times {{180}^ \circ }}}{6} = \frac{{{{720}^ \circ }}}{6} = {120^ \circ }\)
سه تا زاویه \({120^ \circ }\) داریم که می شود \(3 \times {120^ \circ } = {360^ \circ }\).
اگر بخواهیم فقط با استفاده از یک نوع شکل منتظم کاشی کاری کنیم، اندازۀ هر زاویۀ داخلی آن باید شمارندۀ \({360^ \circ }\) باشد؛ به عبارتی \({360^ \circ }\) باید بر اندازۀ هر زاویۀ داخلی شکل منتظم بخش پذیر باشد.
آیا با کاشی هایی به شکل پنج ضلعی منتظم، می توان به تنهایی کاشی کاری کرد؟
اندازۀ هر زاویۀ داخلی \(\frac{{(5 - 2) \times {{180}^ \circ }}}{5} = \frac{{3 \times {{180}^ \circ }}}{5} = \frac{{{{540}^ \circ }}}{5} = {108^ \circ }\) می باشد و 360 بر 108 بخش پذیر نیست.
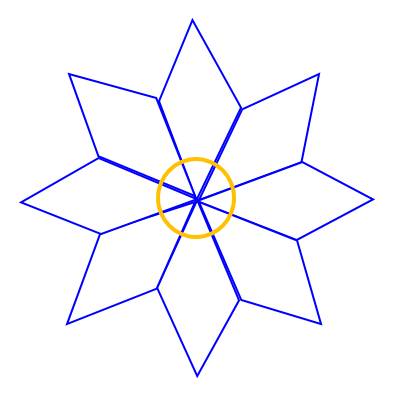
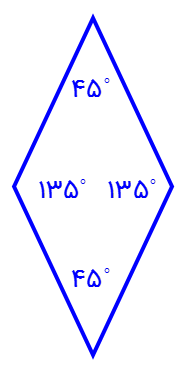
شکل زیر با یک نوع مثلث و یک نوع لوزی کاشی کاری شده است. اندازۀ زاویه های مثلث و لوزی را محاسبه کنید.
اگر به مرکز طرح کاشی کاری دقت کنید، 8 تا زاویۀ تند لوزی ها که با هم مساویند، در کنار هم تشکیل زاویۀ 360 درجه را می دهند. اندازۀ زاویۀ تند در هر لوزی برابر 45 درجه خواهد بود:
\(\frac{{{{360}^ \circ }}}{8} = {45^ \circ }\)
اندازۀ زاویۀ باز در هر لوزی 135 = 45 – 180 می باشد:
سپس به گوشه ای دقت کنید که از دو زاویۀ باز لوزی و یک زاویۀ مثلث تشکیل شده است. اندازۀ یکی از زاویه های مثلث برابر خواهد بود با:
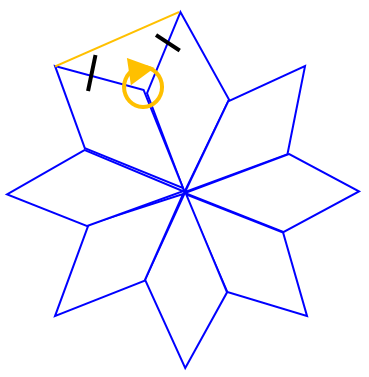
\(\begin{array}{l}2 \times {135^ \circ } = {270^ \circ }\\\\ \Rightarrow {360^ \circ } - {270^ \circ } = {90^ \circ }\end{array}\)
درمثلث قائم الزاویه ای که دو ساق برابر دارد اندازۀ هر زاویۀ تند برابر است با:
\({180^ \circ } - {90^ \circ } = {90^ \circ } \Rightarrow \frac{{{{90}^ \circ }}}{2} = {45^ \circ }\)
برای محاسبه مجموع زاویه های داخلی در n ضلعی های مقعر (کاو) نیز از رابطه \({180^ \circ } \times (n - 2)\) استفاده می کنیم.
تهیه کننده : افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
زاویه های خارجی
فصل 3 : چندضلعی ها
زاویه های خارجی
در چندضلعی های محدب، زاویه ای که در هر رأس بین یک ضلع و امتداد ضلع دیگر تشکیل می شود، زاویۀ خارجی آن رأس نامیده می شود؛ مانند:
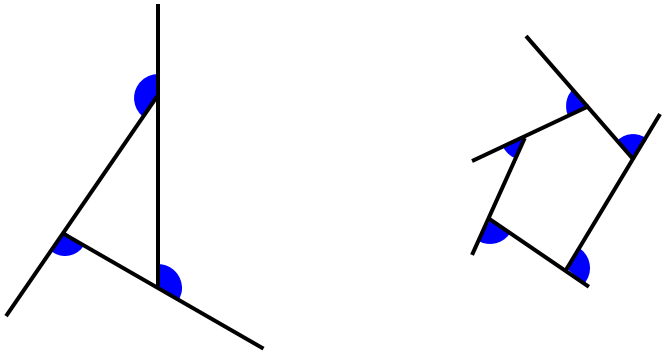
1 در چندضلعی های محدب مجموع هر زاویۀ داخلی با زاویۀ خارجی متناظرش برابر است با \({180^ \circ }\)؛ مانند:
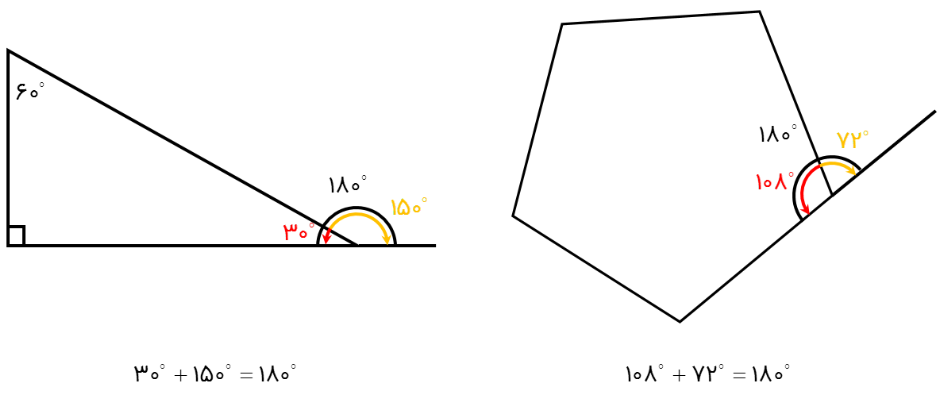
2 در چندضلعی های محدب، مجموع زاویه های خارجی \({360^ \circ }\) است؛ مانند:
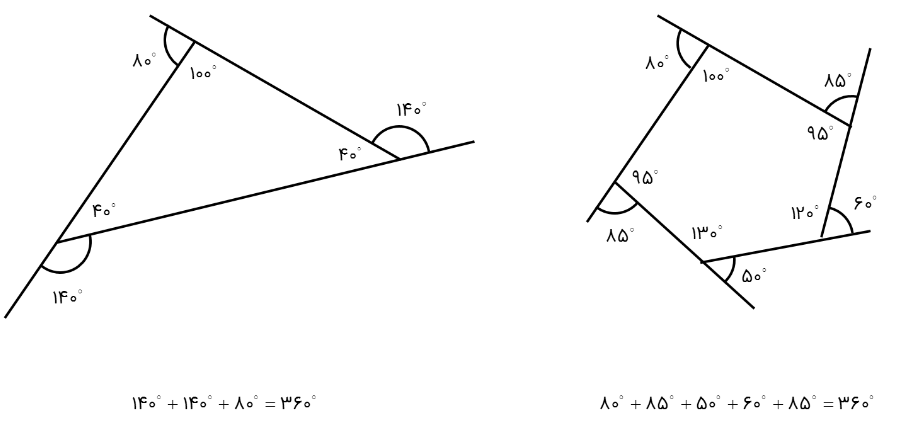
در شکل مقابل، اندازۀ x چند درجه است؟
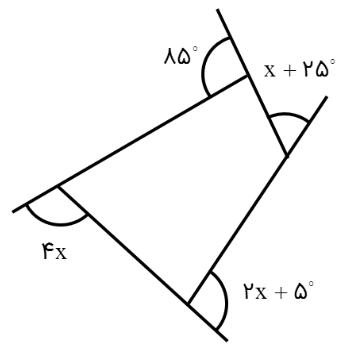
مجموع زاویه های خارجی در چندضلعی های محدب برابر است با 360 درجه:
\(\begin{array}{l}4x + (2x + {5^ \circ }) + (x + {25^ \circ }) + {85^ \circ } = {360^ \circ }\\\\ \Rightarrow 7x + {115^ \circ } = {360^ \circ } \Rightarrow 7x = {360^ \circ } - {115^ \circ } = {245^ \circ }\\\\ \Rightarrow x = \frac{{{{245}^ \circ }}}{7} = {35^ \circ }\end{array}\)
در چندضلعی های منتظم زاویه های خارجی برابرند، بنابراین برای بدست آوردن اندازۀ یک زاویۀ خارجی می توان \({360^ \circ }\) را بر تعداد زاویه های خارجی تقسیم کرد:
اندازۀ هر زاویۀ خارجی\( = \frac{{{{360}^ \circ }}}{n}\)
مثال
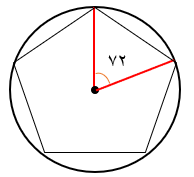
اندازۀ هر زاویۀ خارجی در ده ضلعی منتظم برابر است با: \({360^ \circ } \div 10 = {36^ \circ }\)
اگر اندازۀ یک زاویۀ داخلی n ضلعی منتظمی 156 درجه باشد، تعداد اضلاع چندضلعی را بیابید.
می دانیم مجموع هر زاویۀ خارجی با زاویۀ داخلی متناظرش برابر است با \({180^ \circ }\) . پس اندازۀ هر زاویۀ خارجی n ضلعی منتظم \({180^ \circ } - {156^ \circ } = {24^ \circ }\) . با توجه به اینکه می دانیم مجموع زاویه های خارجی باید \({360^ \circ }\) شود، بنابراین n ضلعی مورد نظر سؤال 15 ضلعی منتظم است:
\({360^ \circ } \div {24^ \circ } = 15\)
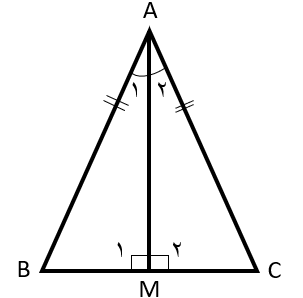
در هر مثلث، اندازۀ هر زاویۀ خارجی با مجموع دو زاویۀ داخلی غیر مجاورش (دو زاویۀ داخلی که کنارش قرار ندارند) برابر است.
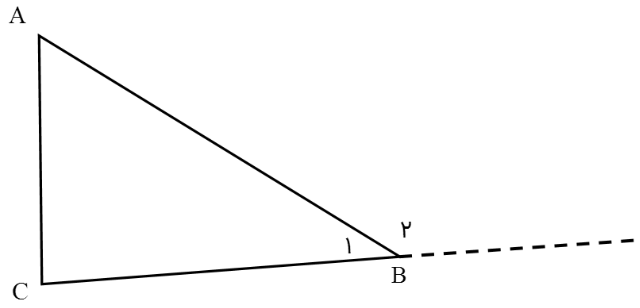
\(\left. \begin{array}{l}\hat A + {{\hat B}_1} + \hat C = {180^ \circ }\\\\{{\hat B}_1} + {{\hat B}_2} = {180^ \circ }\end{array} \right\} \Rightarrow {\hat B_2} = \hat A + \hat C\)
در شکل مقابل زاویۀ x چند درجه است؟
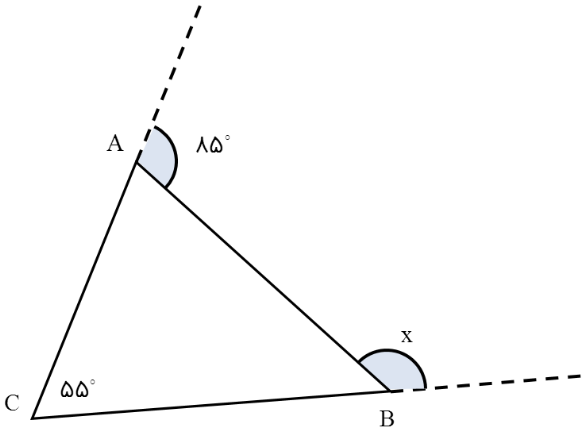
ابتدا زاویۀ داخلی A را به دست می آوریم:
\({180^ \circ } - {85^ \circ } = {95^ \circ }\)
حال با استفاده از نکتۀ قبل زاویۀ x را تعیین می کنیم:
\(x = {95^ \circ } + {55^ \circ } = {150^ \circ }\)
هرگاه روی محیط یک چندضلعی محدب حرکت کنیم به اندازۀ زاویه های خارجی شکل می چرخیم، یعنی \({360^ \circ }\).
مثال
لاک پشتی برای پیمودن محیط 5 ضلعی منتظم از نقطۀ A شروع می کند. وقتی می خواهد از روی ضلع AB روی ضلع BC قرار بگیرد به اندازۀ زاویۀ خارجی B می چرخد و بعد به اندازۀ زاویۀ خارجی C و ... . پس تا وقتی دوباره به نقطۀ A برگردد روی هم \({360^ \circ }\) می چرخد.
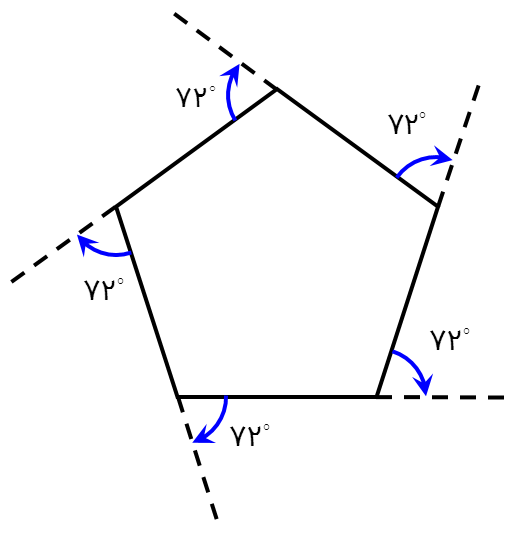
\(5 \times {72^ \circ } = {360^ \circ }\)
تهیه کننده: افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
عبارات جبری
فصل 4 : جبر و معادله
عبارات جبری
هر ترکیبی از عدد یا حروف که به وسیله ی عمل های جبری مانند جمع، تفریق، ضرب و تقسیم به هم مربوط شوند. مانند:
\(5x\,,\,\frac{2}{{3a}}\,,\,9{a^2} - 4c\)
در یک جمله ای ها علامت ضرب بین عدد و حروف، یا ضرب بین حروف را نمی نویسیم یا اگر هم بخواهیم علامت ضرب قرار دهیم با یک نقطه بین حروف، یا با قرار دادن آن ها در پرانتز نشان می دهند.
انواع عبارت های جبری
1- یک جمله ی جبری:
اگر در یک عبارت جبری بین حروف و اعداد فقط از علامت ضرب استفاده شود، آنگاه تشکیل جمله ای می دهد. مانند:
\(2{x^2}\,,\,8{a^3}b\)
2- چند جمله ی جبری:
اگر دو یا چند، یک جمله ای غیرمتشابه را با هم جمع یا تفریق کنیم، آنگاه تشکیل یک چند جمله ای جبری می دهد؛ مانند:
(سه جمله ای) 2a-6+4x
(دو جمله ای) -3a+5b
1هر عدد به توان یک برابر با خودش است:
\({x^1} = x\)
2 یک به توان هر عدد دلخواه، برابر با یک است:
\({1^x} = 1\)
3صفر به توان هر عدد مثبت برابر صفر می شود:
\({0^x} = 0\,\,\,\,\,\,\,\,\,(x > 0)\)
4سه عدد غیرصفر به توان صفر برابر یک می شود:
\({x^0} = 1\,\,\,\,\,\,\,\,\,\,\,\,(x \ne 0)\)
5در ضرب دو عبارت توان دار با پایه های مساوی، یک پایه را نوشته و توان ها را با هم جمع می کنیم:
\({x^a} \times {x^b} = {x^{a + b}}\)
6 مربع یا مجذور یک عدد:
\({x^2}\)
7مکعب یک عدد:
\({x^3}\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جملات متشابه
فصل 4 : جبر و معادله
جملات متشابه
جملاتی که قسمت حروفی و توان آن ها عیناً مثل هم باشند را متشابه گویند.
مثال
در مورد هر قسمت مشخص کنید که جملات متشابه اند.
\((4b\,,\, - 9b)\)(الف
عبارت 4b و -9b با هم متشابه هستند، زیرا قسمت حرفی آن ها یعنی «b» یکسان می باشد.
\(( - \frac{6}{5}{x^2}yz\,,\,3{x^2}yz)\)(ب
عبارت \( - \frac{6}{5}{x^2}yz\) و \(3{x^2}yz\) با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی «\({x^2}yz\) » یکسان می باشد.
از بین جمله های زیر، جمله های متشابه را پیدا کنید و آن ها را مشخص کنید.
\( - 8{x^2}\,,\,\frac{3}{5}xy\,,\,6a{b^2}\,,\,{x^2}\,,\,\frac{3}{4}{b^2}a\,,\,5xy\,,\,4{x^2}\)
1- عبارات \( - 8{x^2}\)و \(4{x^2}\)و \(1{x^2}\)با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی \({x^2}\)یکسان می باشد.
2- عبارات \(\frac{3}{5}xy\) و\(5xy\) باهم متشابه هستند زیرا قسمت حرفی آن ها یعنی\(xy\)یکسان می باشد.
3- عبارات \(6a{b^2}\)و \(\frac{3}{4}a{b^2}\) با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی\(a{b^2}\)یکسان می باشد.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ساده کردن عبارات جبری
فصل 4 : جبر و معادله
ساده کردن عبارت جبری
ابتدا جمله های متشابه را مشخص می کنیم، سپس ضرایب جملات متشابه را جمع یا تفریق کرده و جمله های غیرمتشابه به همان صورت می نویسیم.
مثال
عبارت جبری زیر را ساده کنید.
\(6{m^2} - 5y + 3my + 10{m^2} + 7my = \)(الف
\(\begin{array}{l}6{m^2} - 5y + 3my + 10{m^2} + 7my = \\\\(6 + 10){m^2} - 5y + (3 + 7)my = 16{m^2} - 5y + 10my\end{array}\)
ب)\(3(4x - 5x) + 15{x^2} - 6x = \)
طبق رعایت اولویت ها ابتدا عمل ضرب که مقدم تر بر جمع و تفریق می باشد را انجام می دهیم عدد 3 را در هر یک از یک جمله ای های درون پرانتز ضرب می کنیم و بقیه جمله را می نویسیم سپس بعد از عمل ضرب عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم:
\(\begin{array}{l}3(4x - 5x) + 15{x^2} - 6x = (3 \times 4)x - (3 \times 5)x + 15{x^2} - 6x = \\\\12x - 15x + 15{x^2} - 6x = (12 - 15 - 6)x + 15{x^2} = - 9x + 15{x^2}\end{array}\)
(پ\(2(xy - 4) - (7xy - 8) = \)
یک جمله ای یعنی 2 را در هر یک از جمله های چند جمله ای ضرب می کنیم سپس چند جمله ای که درون پرانتز قرینه می شود. در نتیجه عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم:
\(2(xy - 4) - (7xy - 8) = 2xy - 8 - 7xy + 8 = - 5xy\)
اگر در یک عبارت جبری جمله های متشابه وجود نداشت آن عبارت قابل ساده شدن نیست.
آیا در هر قسمت، جملات مشابه وجود دارند؟
(الف\(4x - 5y\)
با هم متشابه نیستند چون قسمت حرفی آن ها x و y یکسان نمی باشد.
(ب\(2m + 3a - 1\)
با هم متشابه نیستند چون قسمت حرفی آن ها a و m یکسان نمی باشد.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
ضرب عبارت های جبری
فصل 4 : جبر و معادله
ضرب دو جمله ای
ضریب های عددی در هم و متغیرها نیز در هم ضرب می شوند؛ مانند:
\(3a(4b) = (3 \times 4)(a \times b) = 12ab\)
ضریب a یعنی عدد 3 را در ضریب b یعنی عدد 4 ضرب و متغیرها را در هم ضرب می کنیم.
در ضرب متغیرها اگر متغیرها مثل هم باشند به صورت توان دار نوشته می شوند در غیر این صورت کنار هم نوشته می شوند. مثلاً:
\( - 4n( + 2n) = ( - 4 \times 2)(n \times n) = - 8{n^2}\)
ضرب یک جمله ای در چندجمله ای
یک جمله ای در هر یک از جمله های چندجمله ای ضرب می شود. به مثال های زیر توجه کنید:
(الف\(2(5x - 3y) = 2(5x) - 2(3y) = 10x - 6y\)
(ب\(\frac{1}{3}(6a - 12b) + 2( - 5a + 10b) = \frac{1}{3}(6a) - \frac{1}{3}(12b) + \)
\(2( - 5a) + 2(10b) = 2a - 4b - 10a + 20b\)
ابتدا عدد پشت پرانتز را در یک جمله ای های داخل پرانتز ضرب می کنیم و اگر جملات مشابه داشته باشیم، سپس ساده می کنیم و حاصل عبارت را به دست می آوریم.
ضرب چندجمله ای در چندجمله ای
هر یک از جمله های چند جمله ای اول را در همه جمله های دوم ضرب می کنیم سپس عبارت را ساده می کنیم؛ مانند:
\(\begin{array}{l}(x + 2)(x + 1) = x(x) + x(1) + 2(x) + 2(1) = \\\\{x^2} + x + 2x + 2 = {x^2} + 3x + 2\end{array}\)
با توجه به اینکه اولویت ضرب نسبت به جمع و تفریق مقدم تر است برای ساده کردن هر عبارت جبری ابتدا ضرب ها را انجام داده سپس جمع و تفریق انجام می دهیم. به عنوان مثال:
\(\begin{array}{l} - 8{x^2}y + 2x(4xy + 5) = - 8{x^2}y + 2x(4xy) + 2x(5) = \\\\ - 8{x^2}y + 8{x^2}y + 10x = 10x\end{array}\)
جمله ی اول یعنی \( - 8{x^2}y\) را می نویسیم سپس ضرب یک جمله ای در چند جمله ای را طبق توضیحات بالا عمل کرده، یک بار 2x را در جمله ی اول درون پرانتز یعنی 4xy و یک بار 2x را در جمله ی دوم درون پرانتز یعنی 5 ضرب می کنیم و عبارت به دست آمده را ساده می کنیم.
مثال
با توجه به شکل و تساوی مساحت ها در دو قسمت یک تساوی جبری بنویسید.
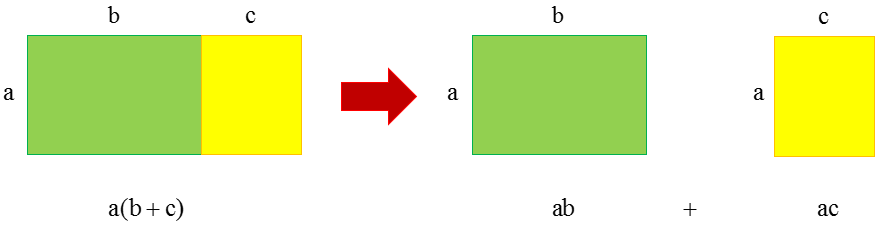
ابتدا یک مستطیل رسم می کنیم و طول آن را به دو قسمت نامساوی تقسیم می کنیم و مساحت آن را به دست می آوریم سپس آن مستطیل را از قسمت طول شکسته و به دو مستطیل با طول های متفاوت ولی عرض های یکسان تقسیم می کنیم سپس مجموع مساحت مستطیل جدید را به دست می آوریم. اگر دو حالت را با هم مقایسه کنیم متوجه می شویم که مساحت هر دو حالت با هم برابر است.
مساحت شکل زیر را با عبارت جبری نشان دهید.
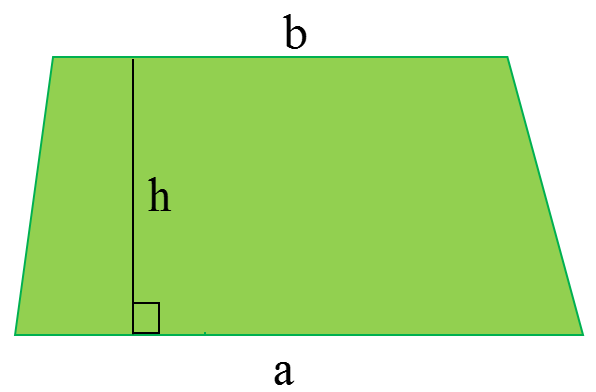
ابتدا مساحت شکل را به صورت فارسی می نویسیم سپس در رابطه به جای کلمات فارسی حروف انگلیسی را قرار می دهیم. در شکل قاعده ها با حروف کوچک a و b و ارتفاع با حرف h نامگذاری شده اند و مساحت را با حرف S نشان می دهیم:
برای به دست آوردن محیط اشکال هندسی مانند تمرین قبل ابتدا محیط شکل موردنظر را به صورت فارسی می نویسیم سپس در رابطه به جای کلمات فارسی حرف انگلیسی را جایگزین می کنیم دقت داشته باشید که محیط را با حرف P نشان می دهیم.
در شکل زیر تعداد چوب کبریت ها در شکل n ام چند تا است؟
به رابطه های زیر در هر شکل توجه کنید. با کمی دقت متوجه می شوید که شماره های هر شکل در 3 ضرب شده سپس یک واحد به آن اضافه شده است بنابراین شکل n ام دارای 3n+1 چوب کبریت خواهد بود.
جمله ی n ام الگوی جبری زیر را بنویسید.
1 , 4 , 9 , 16 , 25 , …
دقت داشته باشید شماره هر جمله در خودش ضرب شده و در زیر عدد مورد نظر می نویسیم الگوی مورد نظر به دست آوردیم جمله ی n ام که مشخص می شود\(n \times n\)برابر می شود \({n^2}\) .
عدد دو رقمی ab را با نماد \(\overline {ab} \) نمایش می دهیم بنابراین \(\overline {ab} = 10a + b\)
عدد 47 ار می توان به صورت گسترده 40+7 یا 4×10+7 نوشت.
نشان دهید مجموع هر عدد دو رقمی با مقلوب آن همواره مضرب 11 می باشد.
\(\overline {ab} + \overline {ba} = 10a + b + 10b + a = 11a + 11b = 11(a + b)\)
عدد دو رقمی را با توجه به نکته ی بالا \(\overline {ab} \) می نویسیم و با مقلوب آن یعنی \(\overline {ba} \) جمع می کنیم و بعد از جایگذاری به جای هر کدام و ساده کردن عبارت حاصل را به دست می آوریم.
نشان دهید تفاضل هر عدد دو رقمی از مقلوبش مضرب 9 است.
\(\overline {ab} - \overline {ba} = 10a + b - (10b + a) = 9a - 9b = 9(a - b)\)
عدد دو رقمی را با توجه به نکته ی بالا \(\overline {ab} \) می نویسیم و مقلوب آن یعنی \(\overline {ba} \) را از آن کم می کنیم و بعد از جایگذاری به جای هر کدام و ساده کردن عبارت حاصل را به دست می آوریم.
92-29=63=9×7
85-58=27=9×3
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
پیدا کردن مقدار یک عبارت جبری
فصل 4 : جبر و معادله
پیدا کردن مقدار یک عبارت جبری
هرعبارت جبری شامل یک یا چند متغیره اگر به جای این متغیرها عدد قرار دهیم حاصل ان عبارت جبری به دست می اید.
در عبارت جبری متغییر را بر میداریم و به جای ان عددی که گفته شده را با پرانتز می گذاریم (اگر پرانتز قرار ندهیم مشکلی پیش نمی اید اما پیشنهاد می کنم همیشه گذاشتن پرانتز را رعایت کنید)
مثال
مقدارعددی هریک از عبارت های زیر را به ازای مقادیر \(a = 2\)و \(b = 3\) حساب کنید.
الف) \(a + 4 = \)
به جای متغییر a مقداری که در سوال داده شده را قرار می دهیم و با عدد بعدی جمع می کنیم و حاصل را به دست می اوریم.
الف) \(a + 4 = (2) + 4 = 6\)
ب)\(2a + 6b = \)
ابتدا عدد 2 را می نویسیم و به جای متغیرa مقدار مورد نظر در سوال را جایگزین می کنیم سپس عدد6 را می نویسیم و به جای متغیرb مقدار داده شده در سوال را جایگزین می کنیم و حاصل را به دست می اوریم.
ب)\(2a + 6b = 2(2) + 6( - 3) = 4 - 18 = - 14\)
وقتی یک عددی قبل از یک متغیری چسبیده باشد و یا وقتی چند تا متغییر به هم چسبیده باشد یعنی بین انها علامت ضرب وجود دارد طبق نکته بالا جایگزین می کنیم و با رعایت اولویت های انجام محاسبات به محاسبه حاصل عبارت می پردازیم.
مثال
عبارت های جبری زیر را به ازای مقادیر داده شده بدست اورید.
الف)\(5xy - 2y + 3{\rm{ (a = - 3 ,b = - 1)}}\)
\(5xy - 2y + 3 = 5(2)( - 1) - 2( - 1) + 3 = - 10 + 2 + 3 = 5\)
در جمله اول و دوم چون عدد به متغیرها چسبیده است، عدد را می نویسیم و به جای متغیرها مقادیر داده شده آن ها را جایگزین می کنیم و بعد عملیات ضرب ، جمع و تفریق را انجام داده و در نتیجه حاصل را به دست می اوریم
ب)\( - 2a + 5{b^2} - 3{a^2}{b^3}{\rm{ (a = - 3 , b = - 1)}}\)
\( - 2a + 5{b^2} - 3{a^2}{b^3}{\rm{ = - 2( - 3) + 5( - 1}}{{\rm{)}}^2} - 3{( - 3)^2}{( - 1)^{ - 3}} = 6 + 5 + 27 = 38\)
در عبارتت داده شده متغیرها توان دار می باشند ابتدا عدد چسبیده به متغیرها را می نویسیم و به جای هر متغیر مقدار داده شده را جایگزین می کنیم و در پرانتز می گذاریم ، سپس هر متغیری که توان دارد، توان ان را بالای پرانتز مقدار جایگزین شده قرار می دهیم و با رعایت اولویت ها به محاسبه حاصل عبارت می پردازیم.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اعداد زوج و فرد
فصل 4 : جبر و معادله
اعداد زوج
از ضرب عدد 2 دریک عدد صحیح ،یک عدد زوج به دست می آید. (اگرk یک عدد صحیح باشد، 2k یک عدد زوج است)
مثال
آیا حاصل جمع دو عدد زوج ،عددی زوج است؟
فرض کنیم a و b دوعدد طبیعی زوج باشد نشان می دهیم:
\(a = 2n{\rm{ }}(n \in N){\rm{ }},{\rm{ }}b = 2m(m \in N) \Rightarrow a + b = 2n + 2m = 2(n + m) = 2k{\rm{ (k}} \in {\rm{n)}}\)
(\(m + n\)را یک عدد طبیعی مانند k فرض می کنیم(
اگر عدد 2 در هر عددی ضرب شود حاصل همواره زوج خواهد بود چون تمام اعداد مضرب 2 هستند.
اعداد فرد
اگر از یک عدد زوج یک واحد کم کنیم یا یک واحد به ان اضافه کنیم عدد فرد به دست می اید.
(اگر h یک عدد صحیح باشد 2h-1 یا 2h-1 یک عدد فرد است)
نشان دهید حاصل ضرب یک عدد زوج در یک عدد فرد عددی زوج است.
فرض می کنیم a عددی طبیعی و زوج و b عددی طبیعی و فرد باشد.
\(a = 2n{\rm{ }},{\rm{ }}b = 2m - 1{\rm{ }},{\rm{ }}(n,m \in N)\)
پس a وb را در هم ضرب میکنیم و مقادیر داده شده را جایگزین می کنیم.
\(a \times b = (2n)(2m - 1) = 2 \times n \times (2m - 1) = 2(2nm - n) = 2c\)
(\(2nm - n\)را یک عدد طبیعی مانند c فرض می کنیم)
حاصل ضرب هر عدد طبیعی در عدد 2، عددی زوج است.
عبارت جبری زیر را به ازای مقادیر داده شده به دست اورید.
\(\frac{{4xy + 3z}}{{ - 2x + 5y}}{\rm{ (x = - 1 , y = 1 , z = 2)}}\)
\(\frac{{4( - 1)(1) + 3(2)}}{{ - 2( - 1) + 5(1)}} = \frac{{ - 4 + 6}}{{ + 2 + 5}} = \frac{2}{7}\)
ابتدا خط کسری را می کشیم و در صورت کسر عدد 4 و3 را با عمل جمع می نویسیم و به جای متغیرها مقادیر داده شده را درون پرانتز جایگزین می کنیم و مخرج کسر را به همین صورت نوشته و محاسبات را انجام داده و حاصل را بدست می اوریم.
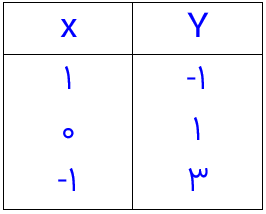
با توجه به رابطه x و y، مقدار y را بدست اورید و جدول را کامل کنید.
\(y = - 2x + 1\)
جای x عدد 1 را در رابطه قرار می دهیم و حاصل به دست امده را در جدول به جای y می گذاریم نقطه های داده شده در x را به همین صورت در رابطه جایگزین می کنیم و مقدار y را به دست می اوریم.
\(\begin{array}{l}y = - 2(1) + 1 = - 2 + 1 = - 1\\\\y = - 2(0) + 1 = 0 + 1 = 0\\\\y = - 2( - 1) + 1 = 2 + 1 = 3\end{array}\)
مثال
چرا مجموع دو عدد فرد عددی زوج می شود؟
\((2k + 1) + (2t + 1) = 2k + 2t + 2 = 2(k + t + 1) \Rightarrow \) مضرب 2است \( \Rightarrow \) زوج است
مثال
مجموع دو عدد که یکی زوج ودیگری فرد باشد ، زوج می شود یا فرد؟چرا؟
\(2m + (2m + 1) = 2n + 2m + 1 = 2(n + m) + 1 \Rightarrow \) عددی فرد است
الف) مساحت کل مکعب مستطیل روبرو را به صورت جبری بنوییسید.
ابتدا فرمول شکل را به صورت جبری مینویسیم
\(s = s' + 2s' \Rightarrow s' = p{\rm{ \times c}} \Rightarrow 2(a + b) \times c = 2ac + 2bc\) کل
وقتی مساحت جانبی یعنی(s’) و مساحت مستطیل یعنی(s) را بدست می اوریم \(s = a \times b = ab\) مستطیل را در را در رابطه جایگزین می کنیم.
\(s = 2ac + 2bc + 2ab = 2(ac + bc + ab)\)
عدد2 را در سه جمله فاکتور می گیریم
ب)اگر\(c = 3{\rm{ , }}b = 6{\rm{ }},{\rm{ }}a = 2\) باشند مساحت کل چقدر می شود؟
بعد از به دست امدن مساحت کل مقادیر داده شده را جایگزین می کنیم:
\(s = 2(12 + 6 + 18) = 72\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
تجزیه عبارت های جبری
فصل 4 : جبر و معادله
تجزیه عبارت های جبری
در تجزیه (تبدیل به ضرب یا فاکتور گیری) عبارت های جبری به روش های زیر عمل می کنیم:
گام1: اگر هر دو عبارت عدد داشتن (ب.م.م) آن دو عدد را می نویسیم.
گام 2: حروف انگیلیسی را با کمترین توانی که در جمله دارند می نویسیم.
گام3: تمام جملات را بر جمله مشترک به دست امده تقسیم کرده و حاصل را داخل پرانتز می نویسیم.
مثال
الف)\(7abc + 3ab\)
ابتدا دو عبارت را تجزیه و عامل مشترک را مشخص می کنیم:
\(\left. \begin{array}{l}7abc = 7a \times b \times c\\\\3ab = 3 \times a \times b\end{array} \right\} \Rightarrow 7abc + 3ab = ab(7c + 3)\)
ب)\(9{x^2}{y^3} - 15{x^3}{y^2}\)
\(\left. \begin{array}{l}9{x^2}{y^2} = 3 \times 3 \times x \times x \times y \times y \times y\\\\15{x^2}{y^2} = 3 \times 5 \times x \times x \times x \times y \times y\end{array} \right\} \Rightarrow 9{x^2}{y^2} - 15{x^2}{y^2} = 3{x^2}{y^2}(3y - 5x)\)
پ)\(\frac{{{x^2}y + {x^2}z}}{{{x^2}y - {x^2}z}}\)
علامت صورت و مخرج شبه هم هستند فقط علامت بین آن ها متفاوت می باشد ،پس یکی از دو عبارت را تجزیه کرده و جایگزین می کنیم در صورت ساده شدن کسر مورد نظر را ساده می کنیم و حاصل را به دست می اوریم.
\(\begin{array}{l}\left. \begin{array}{l}{x^2}y = x \times x \times y\\\\{x^2}y = x \times x \times z\end{array} \right\} \Rightarrow {x^2} = (y + z)\\\\\frac{{{x^2}y + {x^2}z}}{{{x^2}y - {x^2}z}} = \frac{{{x^2}(y + z)}}{{{x^2}(y - z)}} = \frac{{(y + z)}}{{(y - z)}}\end{array}\)
اگر عبارت جبری را بخواهیم به توان برسانیم آن را به تعداد توانش ضرب می کنیم.
مثال
\({(x + y)^2} = (x + y)(x + y) = {x^2} = xy + xy + {y^2} = {x^2} + 2xy + {y^2}\)
ابتدا جمله ای را به صورت ضرب دو پرانتز می نویسیم سپس مراحل ضرب چند جمله ای انجام می دهیم و عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم.
به توان رساندن یک عبارت جبری به این معنا نیست که در هر جمله آن را به توان برسانیم.
\({(x + y)^2} \ne {x^2} + {y^2}\)
عامل های مشترک دوجمله جبری را بنویسید.
الف)\(44{a^2}{\rm{ }},{\rm{ }}88{a^2}b\)
ابتدا(ب.م.م) ، \((44,88) = 44\) را بدست می اوریم حرف \(({a^2})\) مشترک است با توان یکسان .در نتیجه عامل مشترک برابر \(44{a^2}\) می باشد.
عبارت های جبری زیر را ساده کنید.
الف)\((2x - 3y) = \)
\(\begin{array}{l}{(2x - 3y)^2} = (2x - 3y)(2x - 3y)\\\\ = (2x \times 2x) + 2x( - 3y) - 3y(2x) - 3y( - 3y) = 4{x^2} - 6xy - 9{y^2}\\\\ = 4{x^2} - 12xy + 9{y^2}\end{array}\)
ب)\({a^2} + {b^2} - {(a - b)^2}\)
ابتدا چند جمله ای را به صورت ضرب دو پرانتز می نویسیم و طبق مراحل گفته شده حاصل را به دست می اوریم.
\((a - b)(a - b) = {a^2} - ab - ab + {b^2} = {a^2} - 2ab + {b^2}\)
سپس حاصل به دست امده را در عبارت جایگزین می کنیم و عبارت درون پرانتز را قرینه می کنیم.
\( = {a^2} + {b^2} - ({a^2} - 2ab + {b^2}) = {a^2} + {b^2} - {a^2} + 2ab - {b^2} = 2ab\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
معادله و حل آن
فصل 4 : جبر و معادله
معادله
یک تساوی جبری است که به ازای مقادیر خاصی از مجهول برقرارباشد
حل معادله
برای حل یک معادله باید ابتدا تمام مقدارعددی را به یک تساوی انتقال دهیم و در نهایت با تقسیم کردن مقدار عددی به دست امده بر ضریب مجهول جواب معادله بدست می آید.
وقتی عددی را از یک طرف تساوی به طرف دیگر ان انتقال می دهیم علامت ان را باید تغییر دهیم.
مثال
\(7a - 2 = 19\)
\(7a = 19 + 2 \Rightarrow a = \frac{{21}}{7} = 3 \Rightarrow a = 3\)
ابتدا معادله را مرتب می کنیم معلوم ها یک طرف تساوی و مجهول ها در طرف دیگر تساوی قرار می دهیم .سپس بعد از ساده کردن عدد معلوم را بر ضریب مجهول تقسیم می کنیم و مقدار مجهول را به دست می اوریم.
اگر در معادله پرانتز داشته باشیم با رعایت اولویت ها و با انجام ضرب ،پرانتز را از بین می بریم ان گاه معادله را حل می کنیم
مثال
\(12(m - 2) = 6m\)
\(12m - 24 = 6m \Rightarrow 12m - 6m = 24 \Rightarrow 6m = 24 \Rightarrow m = \frac{{24}}{6} \Rightarrow m = 4\)
عدد پشت پرانتز را در هریک از جمله های درون پرانتز ضرب می کنیم سپس معادله را حل می کنیم.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
حل معادلات جبری کسر
فصل 4 : جبر و معادله
حل معادلات جبری کسر
برای حل معادلات جبری کسری به روش زیر عمل می کنیم:
1- حل معادلات کسری به روش طرفین وسطین :
از روش طرفین وسطین زمانی استفاده می کنیم که فقط دو کسر مساوی داشته باشیم در این روش صورت هر کسر در مخرج کسر دیگر ضرب شده و مخرج ها را حذف می کنیم.
مثال
\(\frac{{5x - 3}}{4} = \frac{{2x + 6}}{1}\)
\(\begin{array}{l}1(5x - 3) = 4(2x + 6) \Rightarrow 5x - 3 = 8x + 24 \Rightarrow 5x - 8x = 24 + 3\\\\ \Rightarrow - 3x = 27 \Rightarrow x = \frac{{ - 27}}{3} \Rightarrow x = - 9\end{array}\)
چون عبارت بعد از مساوی مخرج ندارد به آن مخرج 1 می دهیم صورت کسر اولی را باید در1 و صورت کسر دومی را باید در 4 ضرب کنیم.
2- حل معادلات کسری به روش حذف مخرج یا مخرج مشترک:
روش مخرج مشترک گرفتن برای کسرها را بلدیم برای معادلات کسری هم می توانیم همان کار را انجام دهیم اما در معادلات کسری به مخرج کسرها احتیاجی نداریم. به همین دلیل این روش را حذف مخرج می گوییم.
مثال
\(\frac{{x + 2}}{{15}} + \frac{{x + 1}}{{10}} = \frac{{8x + 1}}{{30}}\)
\(\begin{array}{l}\frac{{(x + 2) \times 2}}{{15 \times 2}} + \frac{{(x + 1) \times 3}}{{10 \times 3}} = \frac{{(8x + 1) \times 1}}{{30 \times 1}}{\rm{ , }}\left[ {15,10,30} \right] = 30\\\\2 \times (x + 2) + 3 \times (x + 1) = 8x + 1 \Rightarrow 2x + 4 + 3x + 3 = 8x + 1\\\\2x + 3x - 8x = 1 - 4 - 3 \Rightarrow - 3x = - 6 \Rightarrow x = \frac{{ - 6}}{{ - 3}} \Rightarrow x = 2\end{array}\)
3- حل مسئله به کمک معادله :
ابتدا مجهول را با حروف انگلیسی کوچک در نظر می گیریم آن گاه با توجه به مساله، جمله های فارسی را به عدد و علامت های ریاضی تبدبل می کنیم و با حل معادله جواب را به دست می آوریم.
مثال
از 4 برابر عددی 7 تا کم کردیم حاصل 9 شد ان عدد چیست؟
مورد نظر\(4m = 9 + 7 \Rightarrow 4m = 16 \Rightarrow m = \frac{{16}}{4} \Rightarrow m = 4\)
\(4m = 9 + 7 \Rightarrow 4m = 16 \Rightarrow m = \frac{{16}}{4} \Rightarrow m = 4\)
اعداد متوالی به صورت \((n,n + 1,n + 2, \ldots )\) و اعداد فرد یا زوج متوالی را به صورت \((n,n + 2,n + 4, \ldots )\) نشان دهیم.
مثال
مجموع سه عدد فرد متوالی 57 می باشد عدد کوچکتر چند است؟
\(\begin{array}{l}n + (n + 2) + (n + 4) = 57 \Rightarrow 3n + 6 = 57 \Rightarrow 3n + 57 - 6\\3n = 51 \Rightarrow n = \frac{{51}}{3} \Rightarrow n = 17 \Rightarrow \left\{ {17,19,21} \right\}\end{array}\)
عدد کوچک تر=17
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
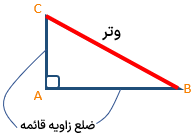
بردارها
فصل 5 : بردار و مختصات
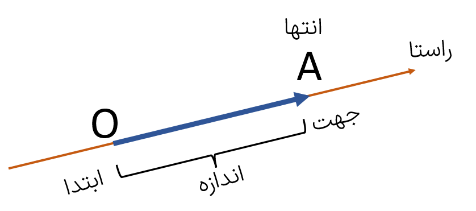
بردار
بردار در ریاضی به پاره خط جهت دار بردار می گوییم. بردار \(OA\) را با \(\overrightarrow {OA} \) نشان می دهیم.
بردارهای برابر
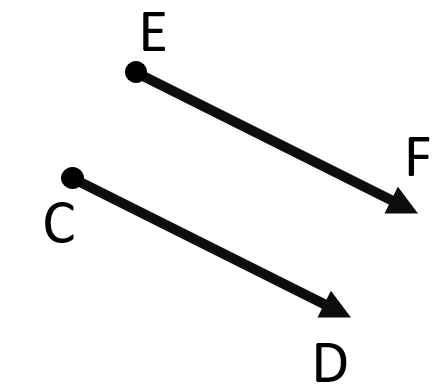
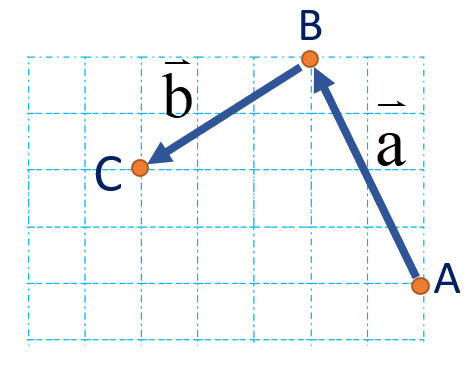
دو بردار وقتی برابرند که هم راستا هم اندازه و هم جهت باشند. مانند بردارهای \(\overrightarrow {CD} \) و \(\overrightarrow {EF} \) :
بردارهای قرینه
دو بردار را قرینه می گوییم وقتی هم راستا و هم اندازه باشند. ولی جهت هایشان عکس یکدیگر باشد مانند دو بردار \(\overrightarrow {AB} \) و \(\overrightarrow {CD} \) در شکل روبرو:
جمع بردارها
فصل 5 : بردار و مختصات
جمع بردارها
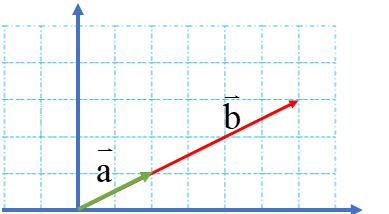
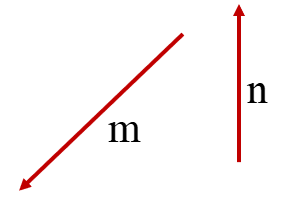
در شکل زیر ابتدا از نقطه ی 1 بردار انتقال a به نقطه ی B می رویم. یعنی ۲ واحد به سمت چپ (افقی) و ۴ واحد به سمت بالا عمودی حرکت می کنیم .
پس بردار انتقال\(\overrightarrow a \)برابر است با \(\overrightarrow a = \left[ \begin{array}{l} - 2\\4\end{array} \right]\) سپس با بردار انتقال \(\overrightarrow b \)از نقطه ی B به نقطه ی C می رویم: \(\overrightarrow b = \left[ \begin{array}{l} - 3\\ - 2\end{array} \right]\)
نقطه ی A با بردار \(\overrightarrow {AC} \) به طور مستقیم به نقطه ی C منتقل شده است. نام آن را بردار انتقال \(\overrightarrow C \) می گذاریم.
می توان گفت \(\overrightarrow C \) کار دو بردار انتقال \(\overrightarrow a \)و \(\overrightarrow b \) را انجام می دهد. به بردار \(\overrightarrow C \) بردار برآیند یا حاصل جمع می گویند.
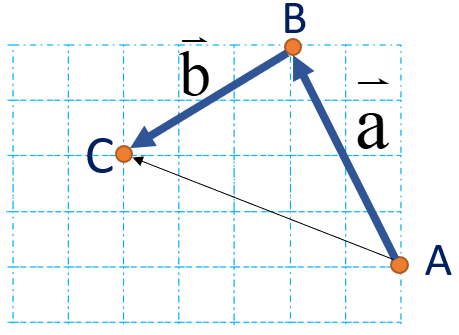
اگر بردار های a و b را با هم جمع کنیم، داریم:
\(\overrightarrow a + \overrightarrow b = \left[ \begin{array}{l} - 2\\ + 4\end{array} \right] + \left[ \begin{array}{l} - 3\\ - 2\end{array} \right] = \left[ \begin{array}{l} - 5\\ + 2\end{array} \right]\)
که حاصل آن طبق شکل بالا برابر \(\overrightarrow {AC} = \overrightarrow c = \left[ \begin{array}{l} - 5\\ + 2\end{array} \right]\) است. بنابراین میتوان یک تساوی برداری به صورت \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) نوشت که تساوی مختصاتی آن هم در بالا نوشته شد.
برای مثال:
در شکل روبرو بردار\(\overrightarrow a \)حاصل جمع دو بردار\(\overrightarrow b \)و \(\overrightarrow c \) است.
جمع برداری :\(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
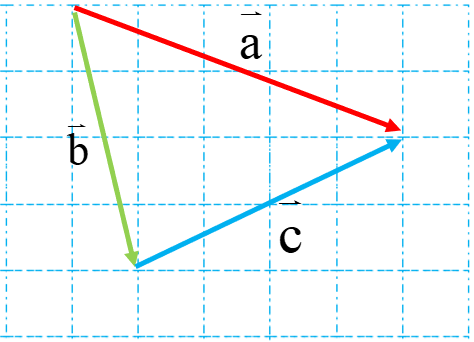
و اگر مختصات آنها را از روی شکل بنویسیم داریم:
جمع مختصاتی: \(\left[ \begin{array}{l} + 1\\ - 4\end{array} \right] + \left[ \begin{array}{l} + 4\\ + 2\end{array} \right] = \left[ \begin{array}{l} + 5\\ - 2\end{array} \right]\)
مثال
برای شکل زیر یک جمع برداری بنویسید.
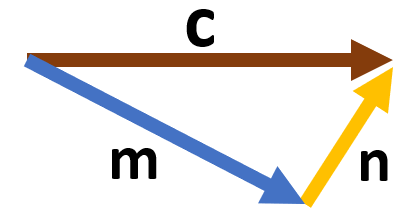
همان طور که می بینیم بردارهای\(\overrightarrow m \) و\(\overrightarrow n \) دنبال هم رسم شده اند. یعنی بردار\(\overrightarrow n \) از انتهای بردار \(\overrightarrow m \) رسم شده است و بردار \(\overrightarrow c \) از اتصال ابتدای \(\overrightarrow n \)به انتهای \(\overrightarrow m \) بدست آمده است پس داریم :\(\overrightarrow m + \overrightarrow n = \overrightarrow c \)
بردارهای مساوی را می توان از نقطه های شروع مختلف رسم کرد.
برای مثال می خواهیم دو بردار مساوی بردار\(\overrightarrow a \) در شکل روبرو رسم کنیم.
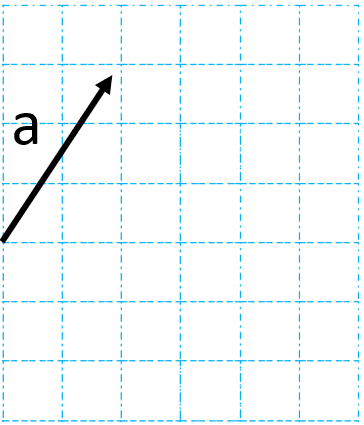
مختصات\(\overrightarrow a \) به صورت \(\overrightarrow a = \left[ \begin{array}{l}2\\3\end{array} \right]\) است. پس مختصات بردارهای رسم شده هم باید همین باشد. می توان بردارهای دیگری نیز مساوی بردار \(\overrightarrow a \)رسم کرد.
حال با استفاده از نکته بالا می خواهیم حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)را رسم کنیم:
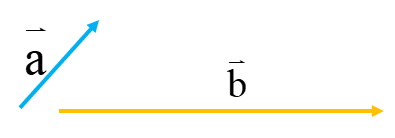
ابتدا دو بردار را دنبال هم رسم می کنیم سپس انتهای\(\overrightarrow a \) را به ابتدای\(\overrightarrow b \) وصل می کنیم بردار حاصل جمع به دست می آید. آن را \(\overrightarrow c \)می نامیم:
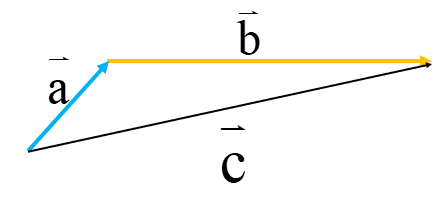
پس: \(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
جمع بردارها خاصیت جابجایی دارد: یعنی اگر در شکل بالا ابتدا \(\overrightarrow b \)را رسم کنیم و سپس\(\overrightarrow a \)را رسم کنیم باز هم بردار حاصل جمع بردار\(\overrightarrow c \)خواهد بود:
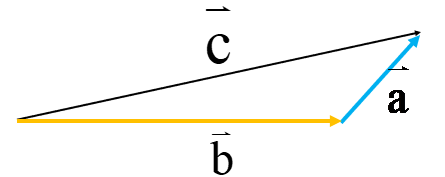
\(\overrightarrow b + \overrightarrow a = \overrightarrow c \)
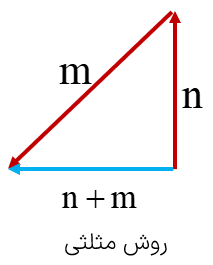
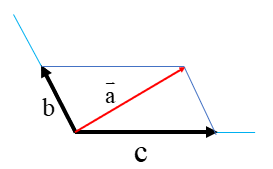
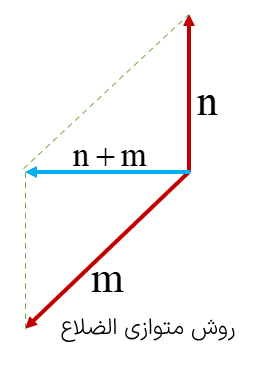
روشی که در بالا برای رسم بردار حاصل جمع گفته شد روش مثلثی نام دارد. روش دیگر برای رسم حاصل جمع دو بردار روش متوازی الاضلاع نام دارد؛ به این صورت که دو بردار را از یک نقطه ی دلخواه به صورت اضلاع مجاور یک متوازی الاضلاع رسم می کنیم، متوازی الاضلاع را تشکیل می دهیم (می دانیم که ضلع های روبروی متوازی الاضلاع با هم برابرند( و قطر متوازی الاضلاع بردار حاصل جمع خواهد بود:
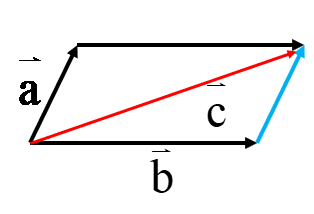
\(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
برای بدست آوردن حاصل جمع سه بردار، ابتدا حاصل جمع دو بردار را به دست می آوریم و سپس بردار حاصل جمع را با بردار سوم جمع می کنیم
مثال
حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)و\(\overrightarrow c \) را بدست آورید.
ابتدا بردار \(\overrightarrow a + \overrightarrow b \) را بدست می آوریم ،سپس آن را با\(\overrightarrow c \) جمع می کنیم:
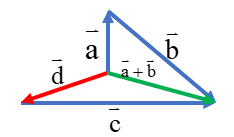
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow a = \overrightarrow d \)
گفتیم که در جمع ترتیب بردارها اهمیتی ندارد، پس می توان ابتدا \(\overrightarrow b + \overrightarrow c \) را بدست آورد. سپس آن را با\(\overrightarrow a \)جمع کرد:
\(\left( {\overrightarrow b + \overrightarrow c } \right) + \overrightarrow a = \overrightarrow d \)
همان طور که میبینید باز هم بردار حاصل جمع\(\overrightarrow d \)بدست می آید.
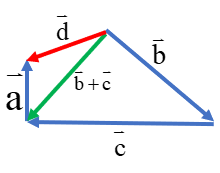
راه حل سوم و البته آسان تر آن است که سه بردار را دنبال هم رسم کنیم (مانند شکل زیر) و سپس ابتدای اولی را به انتهای آخری وصل کنیم:
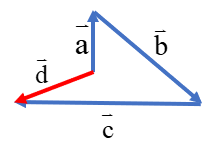
\(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \)
مثال
حاصل جمع بردارهای زیر را رسم کنید.
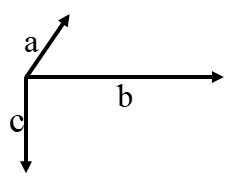
از دو روش قابل حل است:
الف) بردار قرمز حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)است و بردار بنفش بردار\(\overrightarrow a + \overrightarrow b + \overrightarrow c \) است. (روش متوازی الاضلاع)
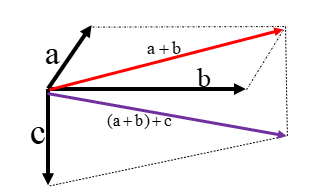
ب) همان طور که می بینید برای بدست آوردن بردار حاصل جمع،کافی است ابتدای بردار اول را به انتهای بردار آخر وصل کنیم.
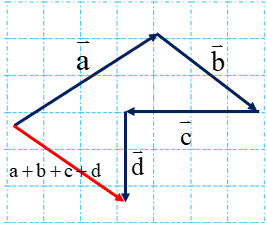
ج) در این قسمت برای تمرین بیشتر از هر دو روش استفاده کردیم.
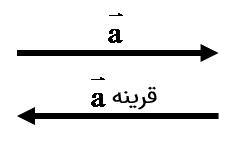
جمع بردارهای قرینه برابر بردار صفر است. آن را با\(\overrightarrow o \) نشان میدهیم و مختصات آن به صورت\(\left[ \begin{array}{l}0\\0\end{array} \right]\) است.
قرینه ی \(\overrightarrow a \)را با \( - \overrightarrow a \) نشان می دهیم:
\(\overrightarrow a + ( - \overrightarrow a ) = \overrightarrow o \)
مثال
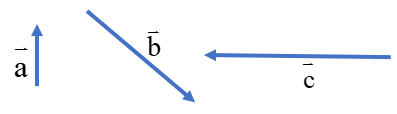
حاصل جمع بردارهای a و b و c چیست؟ چرا؟
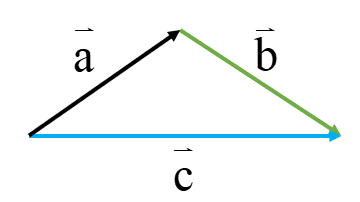
همان طور که می بینید ابتدای بردار a و انتهای بردار C بر یکدیگر منطبق هستند پس حاصل جمع بردارهای a و b و c برابر بردار صفر است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تجزیه ی بردار
فصل 5 : بردار و مختصات
تجزیه ی بردار
تجزیه ی یک بردار در راستاهای داده شده یعنی دو بردار به دست بیاوریم که حاصل جمع آنها بردار داده شده باشد.
در شکل زیر بردار a در راستاهای آبی رنگ تجزیه شده است. همان طور که می بینید تصویر بردار\(\overrightarrow a \)را بر راستاهای داده شده رسم کرده ایم. می توان بردار \(\overrightarrow a \)را به صورت حاصل جمع و نوشت: \(\overrightarrow a = \overrightarrow b + \overrightarrow c \)
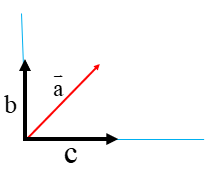
مثال
بردار\(\overrightarrow a \)را در راستاهای داده شده تجزیه کنید بردارهای \(\overrightarrow b \)و\(\overrightarrow c \) را با استفاده از روش متوازی الضلاع طوری رسم می کنیم که \(\overrightarrow b + \overrightarrow c \) برابر بردار \(\overrightarrow a \)شود.
مثال
مختصات دو بردار را که حاصل جمعشان بردار\(\left[ \begin{array}{l}3\\4\end{array} \right]\) باشد، بنویسید.
این سوال جواب های متفاوتی دارد. در اینجا دو تا از آنها را می نویسیم:
\(\begin{array}{l}\left[ \begin{array}{l}1\\2\end{array} \right] + \left[ \begin{array}{l}2\\2\end{array} \right] = \left[ \begin{array}{l}3\\4\end{array} \right]\\\\\left[ \begin{array}{l}3\\1\end{array} \right] + \left[ \begin{array}{l}0\\3\end{array} \right] = \left[ \begin{array}{l}3\\4\end{array} \right]\end{array}\)
در تساوی روبرو x و y را بدست آورید.
\(\left[ \begin{array}{l}3\\ - 4\end{array} \right] + \left[ \begin{array}{l}x\\ - 2\end{array} \right] = \left[ \begin{array}{l}7\\y\end{array} \right]\)
باید جمع طول های دو بردار برابر ۷ و مجموع عرض های آنها برابر شود. بنابراین:
\(\left\{ \begin{array}{l}3 + x = 7\\\\ - 4 + ( - 2) = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 7 - 3 = 4\\\\y = - 4 + ( - 2) = 6\end{array} \right.\)
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
ضرب عدد در بردار
فصل 5 : بردار و مختصات
ضرب عدد در بردار
بردارهای a و b در شکل زیر را در نظر بگیرید:
این دو بردار هم جهت هستند اما اندازه ی بردار b سه برابر اندازه ی بردار a است.مختصات آنها را می نویسیم و با هم مقایسه می کنیم:
\(a = \left[ \begin{array}{l}2\\1\end{array} \right]{\rm{ b = }}\left[ \begin{array}{l}6\\3\end{array} \right]\)
همان طور که می بینید طول و عرض در ۳ ضرب شده اند:
\(3 \times \left[ \begin{array}{l}2\\1\end{array} \right] = \left[ \begin{array}{l}6\\3\end{array} \right]{\rm{ }}3 \times \overrightarrow a = \overrightarrow b \)
اکنون دو بردار زیر را در نظر بگیرید:
همانطور که می بینید این دو بردار هم جهت نیستند در واقع دو جهت مخالف دارند. حال مختصات آنها را می نویسیم:
\(\begin{array}{l}a = \left[ \begin{array}{l}1\\ + 3\end{array} \right]{\rm{ b = }}\left[ \begin{array}{l} + 2\\ - 6\end{array} \right]\\\\( - 2) \times \left[ \begin{array}{l} - 1\\3\end{array} \right] = \left[ \begin{array}{l} + 2\\ - 6\end{array} \right] \Rightarrow ( - 2) \times \overrightarrow a = \overrightarrow b \end{array}\)
این دو بردار هم راستا هستند ولی هم جهت نیستند.پس برای بدست آوردن حاصل ضرب یک عدد در یک بردار آن عدد را در طول و عرض آن بردار ضرب می کنیم:
\(k{\rm{ \times }}\left[ \begin{array}{l}x\\y\end{array} \right] = \left[ \begin{array}{l}kx\\ky\end{array} \right]\)
نتیجه
1 اگر عدد مثبتی را در یک بردار ضرب کنیم بردار حاصل هم راستا و هم جهت بردار اولی است.
2 گر یک عدد منفی در بردار ضرب ،شود بردار ،حاصل هم راستا ولی در خلاف جهت بردار اولی است.
اگر بردار b قرینه ی بردار a باشد: (شکل روبرو)
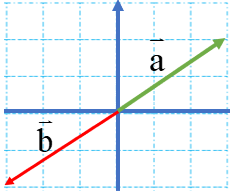
می نویسیم:
\(\begin{array}{l}\overrightarrow b = - \overrightarrow a {\rm{ , }}\overrightarrow b = {\rm{(}} - 1{\rm{)}} \times \overrightarrow a \\\\\overrightarrow a = \left[ \begin{array}{l}x\\y\end{array} \right] \Rightarrow \overrightarrow b = - \overrightarrow a = \left[ \begin{array}{l} - x\\ - y\end{array} \right]\end{array}\)
مثال
با توجه به بردارهای داده شده بردار مورد نظر را رسم کنید.
\(\begin{array}{l}\overrightarrow b = 3\overrightarrow a {\rm{ }}\\\\\overrightarrow y = - 2\overrightarrow x {\rm{ }}\\{\rm{ }}\\\overrightarrow b = \frac{1}{2}\overrightarrow a {\rm{ }}\\{\rm{ }}\\\overrightarrow y = - \frac{3}{2}\overrightarrow x \end{array}\)
\(\begin{array}{l}\overrightarrow b = 3\overrightarrow a {\rm{ }}\\\\\overrightarrow y = - 2\overrightarrow x {\rm{ }}\\{\rm{ }}\\\overrightarrow b = \frac{1}{2}\overrightarrow a {\rm{ }}\\{\rm{ }}\\\overrightarrow y = - \frac{3}{2}\overrightarrow x \end{array}\)
در هر مورد می توانیم مختصات هر بردار و بردار حاصل ضرب را نیز بدست آوریم:
برای مثال:
\(\overrightarrow x = \left[ \begin{array}{l} - 2\\ - 2\end{array} \right] \Rightarrow \overrightarrow y = - \frac{3}{2} \times \left[ \begin{array}{l} - 2\\ - 2\end{array} \right] = \left[ \begin{array}{l}3\\3\end{array} \right]\)
هم چنین برای بردار a می توانیم بنویسیم:
\(\overrightarrow a = \left[ \begin{array}{l} - 2\\0\end{array} \right] \Rightarrow \overrightarrow b = \frac{1}{2} \times \left[ \begin{array}{l} - 2\\0\end{array} \right] = \left[ \begin{array}{l} - 1\\0\end{array} \right]\)
مثال
بردارهای a و b مفروض هستند.
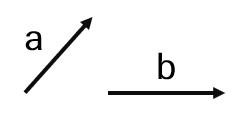
الف) بردار\(\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b \) را رسم کنید.
ابتدا بردارهای a و b را از نقطه ی دلخواه O رسم می کنیم؛ سپس بردارهای\(\overrightarrow a + 3\overrightarrow b \) و\(3\overrightarrow a \) را رسم می کنیم و سپس بردار حاصل جمع C را پیدا می کنیم.
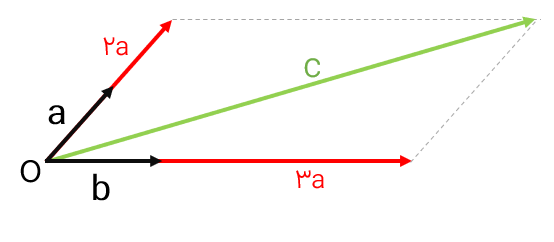
ب) بردار \(\overrightarrow d = \overrightarrow a - \overrightarrow b \) را رسم کنید.
باید بردارهای \(\overrightarrow a \) و\( - \overrightarrow b \) را با هم جمع کنیم. ابتدا بردارهای\(\overrightarrow a \)و\( - \overrightarrow b \) را از یک نقطه رسم می کنیم (روش متوازی الاضلاع)
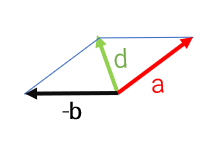
یا دنبال هم رسم می کنیم (روش مثلثی) و همانطور که می بینید بردار حاصل جمع در هر دو شکل یکسان است.
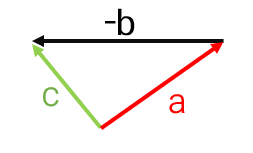
با توجه به بردارهای روبرو، بردار c را رسم کنید.
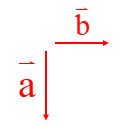
\(\overrightarrow c = 2\overrightarrow a - 3\overrightarrow b = 2\overrightarrow a + ( - 3\overrightarrow b )\)
ابتدا بردارهای \( - 3\overrightarrow b {\rm{ }},{\rm{ }}2\overrightarrow a \) را از یک نقطه رسم می کنیم سپس به روش متوازی الاضلاع بردار حاصل جمع را رسم می کنیم.
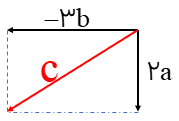
در هر شکل بردار c را بر حسب بردارهای a و b بنویسید.
الف)
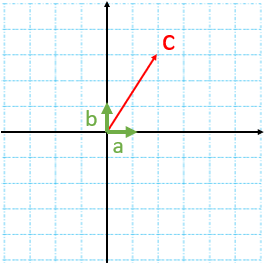
ب)
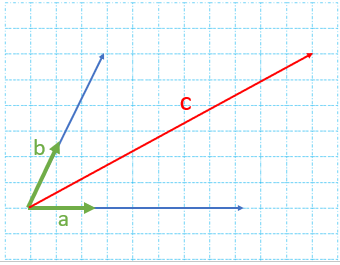
الف) بر حسب نوشتن یعنی بردار c را به صورت حاصل جمع مضرب هایی از بردارهای a و b بنویسیم. اگر متوازی الاضلاعی تشکیل دهیم که بردار c قطر آن باشد. مانند شکل روبرو : (در شکل روبرو طول بردارهای a و b هر کدام یک واحد است)
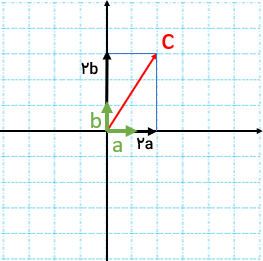
بردار c برابر می شود با \(\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b \)
ب) در این مثال میتوانیم طول بردارهای a و b را با خط کش اندازه بگیریم.
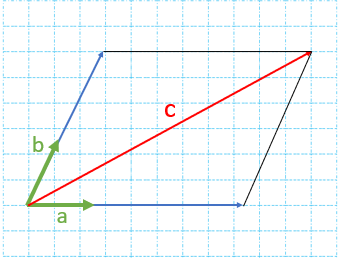
\(\overrightarrow c = 4\overrightarrow a + 2\overrightarrow b \)
با توجه به بردارهای a و b بردارهای c و d را رسم کنید.
\(\begin{array}{l}\overrightarrow c = 4\overrightarrow a - 2\overrightarrow b \\\\\overrightarrow d = ( - 4\overrightarrow a ) + \overrightarrow b \end{array}\)
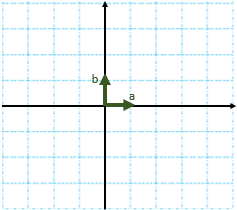
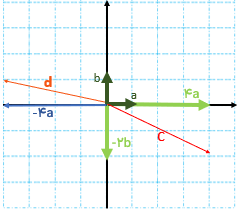
حاصل عبارت روبرو را بدست آورید.
\( - 4\left[ \begin{array}{l} - 5\\7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \)
\( - 4\left[ \begin{array}{l} - 5\\7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 4 \times ( - 5)\\ - 4 \times 7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l}20 - 2\\ - 1\end{array} \right] = \left[ \begin{array}{l}18\\ - 27\end{array} \right]\)
معادله های مختصات زیر را حل کنید (توجه کنید که در اینجا یک بردار است.)
الف) \(\left[ \begin{array}{l}2\\5\end{array} \right] + x = \left[ \begin{array}{l} - 4\\6\end{array} \right] \Rightarrow \)
ب)\( - 3x = \left[ \begin{array}{l}15\\ - 9\end{array} \right] \Rightarrow \)
الف)\(\left[ \begin{array}{l}2\\5\end{array} \right] + x = \left[ \begin{array}{l} - 4\\6\end{array} \right] \Rightarrow x = \left[ \begin{array}{l} - 4\\6\end{array} \right] - \left[ \begin{array}{l}2\\5\end{array} \right] = \left[ \begin{array}{l} - 4 - 2\\6 - 5\end{array} \right] = \left[ \begin{array}{l} - 6\\1\end{array} \right]\)
ب)\( - 3x = \left[ \begin{array}{l}15\\ - 9\end{array} \right] \Rightarrow x = \left[ \begin{array}{l}\frac{{15}}{{ - 3}}\\\frac{{ - 9}}{{ - 3}}\end{array} \right] = \left[ \begin{array}{l} - 5\\3\end{array} \right]\)
با توجه به بردارهای a و b مختصات بردار c را بدست آورید.
\(\overrightarrow a = \left[ \begin{array}{l}2\\1\end{array} \right],\overrightarrow b = \left[ \begin{array}{l} - 2\\3\end{array} \right]{\rm{ }} \to {\rm{ }}\overrightarrow c = \overrightarrow a - 2\overrightarrow b \)
مختصات بردارهای a و b را در معادله ی بالا جایگزین می کنیم
\(\overrightarrow c = \overrightarrow a - 2\overrightarrow b = \left[ \begin{array}{l}2\\1\end{array} \right] - 2\left[ \begin{array}{l} - 2\\3\end{array} \right] = \left[ \begin{array}{l}2 + 4\\1 - 6\end{array} \right] = \left[ \begin{array}{l}6\\ - 5\end{array} \right]\)
بردار داده شده را روی امتدادهای رسم شده تجزیه کنید.
به روش متوازی الاضلاع عمل می کنیم :
بردارهای واحد مختصات
فصل 5 : بردار و مختصات
بردارهای واحد مختصات
همان طور که می دانیم برای اندازه گیری هر کمیتی از یک واحد استفاده می کنیم. مثلا واحد اندازه گیری زمان ساعت یا دقیقه یا ثانیه است و واحد اندازه گیری زاویه درجه است برای اندازه گیری بردار نیز به واحد نیاز داریم این واحد باید از جنس بردار باشد با توجه به اینکه بردار در صفحه ی مختصات با دو محور نمایش داده می شود به واحدی روی هر دو محور نیاز داریم:
بردار \(\overrightarrow i \) بردار واحد طول و بردار\(\overrightarrow j \)بردار واحد عرض نام دارد.مختصات آنها به صورت زیر است.
\(\overrightarrow i = \left[ \begin{array}{l}1\\0\end{array} \right],\overrightarrow j = \left[ \begin{array}{l}0\\1\end{array} \right]\)
هر بردار را می توانیم به صورت حاصل جمع مضرب هایی از دو بردار\(\overrightarrow i \)و \(\overrightarrow j \)بنویسیم.
مثلا در شکل زیر بردار\(\overrightarrow a \)برابر است با : \(\overrightarrow a = 4\overrightarrow i + 2\overrightarrow j \)
همچنین می توانیم مختصات بردار\(\overrightarrow c \)را با استفاده از بردارها \(\overrightarrow i \)
و
\(\overrightarrow j \)واحد بدست آوریم.
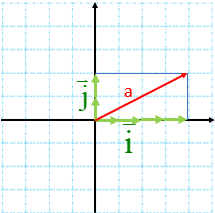
مثال
بردار\(\overrightarrow c \) را بر حسب بردارهای\(\overrightarrow i \) و \(\overrightarrow j \)و سپس به صورت مختصاتی بنویسید.
با توجه به شکل می توانیم بنویسیم:\(\overrightarrow c = - 3\overrightarrow i + \overrightarrow j \)
و مختصات آن:
\(\overrightarrow c = - 3\left[ \begin{array}{l}1\\0\end{array} \right] + \left[ \begin{array}{l}0\\1\end{array} \right] = \left[ \begin{array}{l} - 3 + 0\\0 + 1\end{array} \right] = \left[ \begin{array}{l} - 3\\1\end{array} \right]\)
مثال
بردار زیر را بر حسب\(\overrightarrow i \) و\(\overrightarrow j \) بنویسید.
\(\left[ \begin{array}{l}3\\4\end{array} \right]\)
\(\left[ \begin{array}{l}3\\4\end{array} \right] = 3\left[ \begin{array}{l}1\\0\end{array} \right] + 4\left[ \begin{array}{l}0\\1\end{array} \right] = 3\overrightarrow i + 4\overrightarrow j \)
از این پس می توانیم به صورت مختصر بنویسیم:
\(\left[ \begin{array}{l}2\\ - 5\end{array} \right] = 2\overrightarrow i - 5\overrightarrow j {\rm{ , }}\left[ \begin{array}{l}0\\ - 6\end{array} \right] = \overrightarrow i - 6\overrightarrow j = - 6\overrightarrow j {\rm{ , }}\left[ \begin{array}{l}2\\0\end{array} \right] = 2\overrightarrow i + 0\overrightarrow j = 2\overrightarrow i \)
طرف دوم تساوی های زیر را بنویسید.
\(\begin{array}{l}\overrightarrow i + \overrightarrow j = {\rm{ }}\\2\overrightarrow i - \overrightarrow j = {\rm{ }}\\3\overrightarrow j = \end{array}\)
\(\begin{array}{l}\overrightarrow i + \overrightarrow j = \left[ \begin{array}{l}1\\1\end{array} \right]{\rm{ }}\\2\overrightarrow i - \overrightarrow j = \left[ \begin{array}{l}2\\ - 1\end{array} \right]{\rm{ }}\\3\overrightarrow j = \left[ \begin{array}{l}0\\3\end{array} \right]\end{array}\)
معادله ی برداری زیر را حل کنید.
\(2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = \)
برای حل معادله های برداری می توانیم از دو روش استفاده کنیم:
۱- روش بردارهای واحد\(\overrightarrow j ,\overrightarrow i \)
۲- روش مختصاتی
۱- روش بردارهای واحد:
در این روش مانند حل معادله علامت جملات پس از انتقال به طرف دیگر معادله تغییر می کند و جملات مشابه با هم جمع می شوند.
\(\begin{array}{l}2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = - 6\overrightarrow i + 3\overrightarrow j \\\\3\overrightarrow x = - 6\overrightarrow i + 3\overrightarrow j - 2\overrightarrow i + \overrightarrow j \\\\3\overrightarrow x = ( - 6 - 2)\overrightarrow i + (3 + 2)\overrightarrow j \\\\3\overrightarrow x = - 8\overrightarrow i + 4\overrightarrow j \\\\\overrightarrow x = \frac{{ - 8}}{3}\overrightarrow i + \frac{4}{3}\overrightarrow j \end{array}\)
۲- روش مختصاتی
در این روش مختصات بردارها را می نویسیم.
\(\begin{array}{l}2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right]\\\\\left[ \begin{array}{l}2\\ - 1\end{array} \right] + 3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right]\\\\3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 6 - 2\\3 - ( - 1)\end{array} \right]\\\\3\overrightarrow x = \left[ \begin{array}{l} - 8\\4\end{array} \right] \Rightarrow \overrightarrow x = \left[ \begin{array}{l}\frac{{ - 8}}{3}\\\frac{4}{3}\end{array} \right]\end{array}\)
مثال
اگر \(\overrightarrow a = 3\overrightarrow i - 2\overrightarrow j \) و \(\overrightarrow b = 2\overrightarrow i + \overrightarrow j \) مختصات بردارهای x و y را بدست آورید.
\(\begin{array}{l}\overrightarrow x = 5\overrightarrow a + 3\overrightarrow b {\rm{ }}\\\\\overrightarrow y = \overrightarrow a - 2\overrightarrow b \end{array}\)
بردارهای a و b را در معادله ی داده شده جایگزین می کنیم.
\(\begin{array}{l}\overrightarrow x = 5\overrightarrow a + 3\overrightarrow b = 5(3\overrightarrow i + \overrightarrow j ) + 3(2\overrightarrow i + \overrightarrow j ) = \\\\ \Rightarrow 15\overrightarrow i - 10\overrightarrow j + 6\overrightarrow i + 3\overrightarrow j = (15 + 6)\overrightarrow i + ( - 10 + 3)\overrightarrow j = 21\overrightarrow i - 7\overrightarrow j \\\\\overrightarrow y = \overrightarrow a - 2\overrightarrow b = 3\overrightarrow i - 2\overrightarrow j - 2(2\overrightarrow i + \overrightarrow j ) = \\\\ \Rightarrow 3\overrightarrow i - 2\overrightarrow j - 4\overrightarrow i - 2\overrightarrow j = - \overrightarrow i - 4\overrightarrow j \end{array}\)
بردار \(\overrightarrow b = \left[ \begin{array}{l} - 2\\3\end{array} \right]\) را در دستگاه مختصات و رسم کنید، و آن را بر حسب بردارهای واحد و بنویسید.
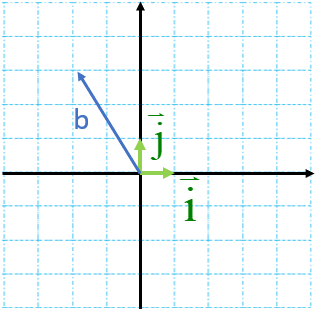
\(\overrightarrow b = - 2\overrightarrow i + 3\overrightarrow j \)
با توجه به شکل زیر مختصات بردار c را با دو روش زیر پیدا کنید.
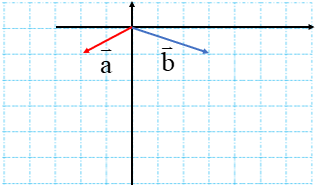
\(\overrightarrow c = 2\overrightarrow a + \overrightarrow b \)
الف) رسم شکل و نوشتن مختصات بردار c از روی شکل:
ابتدا بردار 2a را رسم می کنیم و سپس آن را با بردار bجمع می کنیم با توجه به شکل روبرو مختصات بدست می آید:
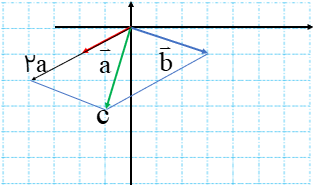
\(\overrightarrow c = \left[ \begin{array}{l} - 1\\ - 3\end{array} \right]\)
ب) پیدا کردن مختصات a و b و قرار دادن آنها در معادله ی :
\(\overrightarrow c = 2\overrightarrow a + \overrightarrow b = 2\left[ \begin{array}{l} - 2\\ - 1\end{array} \right] + \left[ \begin{array}{l}3\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 4 + 3\\ - 2 - 1\end{array} \right] = \left[ \begin{array}{l} - 1\\ - 3\end{array} \right]\)
روش الف هندسی و با استفاده از رسم است و حتما باید از کاغذ شطرنجی استفاده کنیم یا اندازه گیری دقیق انجام دهیم، اما روش ب سریع تر ما را به پاسخ یعنی مختصات c می رساند.
می دانیم اگر طول و عرض یک بردار هر دو مثبت باشند.شکل تقریبی آن به صورت روبرو خواهد بود،حال می توانیم جدول زیر را کامل کنیم:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مثلث و اجزاء آن
فصل 6 : مثلث
انواع مثلث ها
۱) مثلث مختلف الاضلاع
۲) مثلث متساوی الساقين
۳) مثلث متساوی الاضلاع
۴) مثلث قائم الزاويه
۵) مثلث قائم الزاویه ی متساوی الساقین
می دانید که هر مثلث دارای اجزایی است. به سه زاویه و سه ضلع مثلث اجزای اصلی آن می گویند. به طور مثال A,B,Cراس های مثلث، AC AB و BC نام اضلاع و\(\hat a,\hat b,\hat c\) نام زوایای مثلث هستند.
اجزاء فرعی مثلث
به نیمساز ارتفاع عمود منصف و .... اجزای فرعی مثلث می گویند .
نیمساز :
نیم خطی است که از راس شروع شده و زاویه را به دو قسمت مساوی تقسیم می کند.
ارتفاع:
پاره خطی است که از راس مثلث به ضلع مقابل متصل شده و بر آن عمود باشد .
عمود منصف :
خطی است که از وسط ضلع بر آن عمود شده باشد.
میانه:
پاره خطی که از یک راس مثلث به وسط ضلع مقابلش وصل شده باشد.
تهیه کنندگان: شهریار ارم و ندا بهرامی نیا
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
رابطه ی فیثاغورس
فصل 6 : مثلث
رابطه ی فیثاغورس
همانطور که می دانید یکی از انواع مثلث ها مثلث قائم الزاویه است در مثلث قائم الزاویه ضلع مقابل به زاویه ی قائمه که بزرگترین ضلع مثلث است را وتر می نامیم در شکل زیر مثلث ABC قائم الزاویه و \(\hat A = 90^\circ \) این مثلث دو ضلع AB و AC اضلاع زاویه ی قائمه و ضلع BC وتر مثلث است.
فيثاغورس ( فیلسوف و ریاضیدان یونانی ) با تحقیق بر روی مثلث قائم الزاویه به این نتیجه رسید:
(مساحت مربعی که با وتر مثلث قائم الزاویه ساخته میشود برابر است با مجموع مساحت دو مربعی که با اضلاع زاویه ی قائمه ساخته می شود.)
این رابطه بعدها رابطه ی فیثاغورس نامیده شد. طبق شکل زیر مساحت هر شکل کنار آن نوشته شده است . بنابراین :
\(c = 5 \Rightarrow \) مساحت مربع روی وتر:\({c^2} = 25\)
\(\left. \begin{array}{l}a = 3 \Rightarrow {a^2} = 9\\\\b = 4 \Rightarrow {b^2} = 16\end{array} \right\} \Rightarrow \) مجموع مساحت ها :9+16=25
با مقایسه ی دو عبارت داریم:
\({c^2} = {a^2} + {b^2}\)
در هر مثلث قائم الزاويه مجذور وتر برابر است با مجموع مجذور دو ضلع زاویه ی قائمه.
(توضیح: به توان دوم یک عدد مربع یا مجذور آن عدد می گویند به طور مثال مربع یا مجذور ۷ برابر است با \({7^2}\) یا 49)
برعکس این رابطه نیز برقرار است یعنی اگر در مثلثی رابطه ی فیثاغورس برقرار باشد ( مجذور وتر با مجموع مجذور دو ضلع زاویه ی قائمه برابر باشد) آن مثلث حتما قائم الزاویه است.
از این ویژگی برای تعیین اندازه ی اضلاع مثلث قائم الزاویه یا تشخیص نوع مثلث استفاده می کنیم.
برای مثلث ABC را در نظر بگیرید.
۶۴=۸×۸ : مساحت مربعی به ضلع AB
۳۶=۶×۶ : مساحت مربعی به ضلع BC
بنابراین طبق رابطه ی فیثاغورس داریم64+36=100 : مساحت مربعی به ضلع AC پس \(AC = \sqrt {100} = 10\)
مثال
با توجه به اندازه های داده شده در شکل مقابل مقدار x را به دست آورید.
طبق رابطه فیثاغورس داریم :
\(\begin{array}{l}{x^2} = {2^2} + {5^2} = 4 + 25 = 29\\ \Rightarrow \sqrt {29} \end{array}\)
با توجه به این مثال که \({(\sqrt 3 )^2} = \sqrt 3 \times \sqrt 3 = \sqrt 9 = 3\) ؛ اگر a عددی مثبت باشد همواره رابطه ی\({(\sqrt a )^2} = a\) برقرار است.
آیا مثلثی با اضلاع \(\sqrt {11} ,6,5\) قائم الزاویه است؟
\(\left. \begin{array}{l}{6^2} = 36\\\\{5^2} + {(\sqrt {11} )^2} = 11 + 25 = 36\end{array} \right\} \Rightarrow {6^2} = {5^2} + {(\sqrt {11} )^2}\)
بنابراین مثلث مورد نظر قائم الزاویه است.
دقت کنیم در شکل هایی که مجهول ، ضلع زاویه ی قائمه است از معادل های دیگر رابطه ی فیثاغورس
استفاده کنیم.
\({c^2} = {a^2} + {b^2} \Rightarrow \left\{ \begin{array}{l}{a^2} = {c^2} - {b^2}\\{b^2} = {c^2} - {a^2}\end{array} \right.\)
در شکل مقابل مقدار b را به دست آورید.
با توجه به شکل زیر مثلث قائم الزاویه ای به وتر ۱۱ و ضلع قائمه ی ۲ واحد به وجود می آید و بنا به رابطه ی فیثاغورس داریم:
\(\begin{array}{l}{b^2} = {11^2} - {2^2} = 121 - 4 = 117\\ \Rightarrow b = \sqrt {117} \end{array}\)
به کمک رابطه ی فیثاغورس محیط شکل زیر را به دست آورید.
برای محاسبه ی محیط باید مقدار z را به دست آورد بنابراین باید به ترتیب مقادیر x و y و z را محاسبه کنیم.
طبق شکل شماره ۱, X وتر مثلث قائم الزاویه ی متساوی الساقین است.بنابراین داریم:
\({x^2} = {1^2} + {1^2} = 1 + 1 = 2 \Rightarrow x = \sqrt 2 \)
با جایگذاری مقدار x در شکل شماره ۲ داریم:
\({y^2} = {1^2} + {(\sqrt 2 )^2} = 1 + 2 = 3 \Rightarrow y + \sqrt 3 \)
و با جایگذاری مقدار ۷ در شکل شماره ۳ داریم:
\({z^2} = {1^2} + {(\sqrt 3 )^2} = 1 + 3 = 4 \Rightarrow z = \sqrt 4 = 2\)
بنابراین مقدار محیط شکل عبارت است از:
\(p = 1 + 1 + 1 + 1 + 2 = 6\)
با استفاده از رابطه ی فیثاغورس پاره خطی به طول \(\sqrt {10} \) رسم کنید.
به کمک رابطه ی فیثاغورس به دو مربع نیاز داریم که مجموع مساحت آنها ۱۰ باشد. به طور مثال با انتخاب مربع هایی به مساحت های ۱ و ۹ (به ضلع ۱ و ۳ سانتیمتر) برای اضلاع مثلث قائم الزاويه طبق رابطه ی فیثاغورس مساحت مربعی که روی وتر ساخته می شود ۱۰ سانتیمتر مربع است پس ضلع این مربع \(\sqrt {10} \) خواهد بود.
\({x^2} = {1^2} + {3^2} = 1 + 9 = 10 \Rightarrow x = \sqrt {10} \)
بنابراین کافی است به کمک خط کش و گونیا مثلثی قائم الزاویه که اضلاع زاویه ی قائمه ی آن ۱ و ۳ سانتی متر هستند، ترسیم کنیم. وتر مثلث ترسیم شده همان پاره خط موردنظر به اندازه ی \(\sqrt {10} \) خواهد بود.
در شکل مقدار xرا به کمک رابطه فیثاغورس به دست اورید.
\(\begin{array}{l}{x^2} = {6^2} + {6^2} = 36 + 36 = 72\\ \Rightarrow x = \sqrt {72} \end{array}\)
تهیه کنندگان: شهریار ارم و ندا بهرامی نیا
شکل های هم نهشت
فصل 6 : مثلث
شکل های هم نهشت
اگر بتوانیم شکلی را با یک یا چند تبدیل (انتقال تقارن و دوران) بر شکل دیگری منطبق کنیم طوری که کاملا یکدیگر را بپوشانند میگوییم آن دو شکل هم نهشتند در واقع دو شکل هم نهشت با هم قابل انطباق اند.
مثال 1 دو شکل A و B با انتقال بر هم منطبق می شوند.
مثال ۲ دو شکل E و F با تقارن محوری نسبت به خط d بر هم منطبق می شوند .
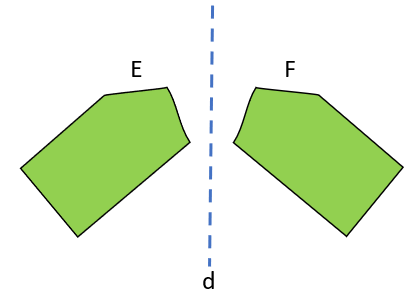
برای نشان دادن هم نهشتی بین دو شکل از علامت\( \cong \) استفاده می کنیم به طور مثال در بالا داریم:
\(E \cong F{\rm{ }},{\rm{ }}A \cong B\)
اجزاء متناظر
اضلاع و زاویه هایی هستند که در هر دو شکل هم نهشت با هم برابرند.
مثال دو مثلث ABC و DEF با دوران بر هم منطبق می شوند. اجزاء متناظر در این دو شکل عبارتند از :
\(A\mathop B\limits^\Delta C \cong D\mathop E\limits^\Delta F \Rightarrow \left\{ \begin{array}{l}\overline {AB} = \overline {DF} ,\hat A = \hat F\\\overline {AC} = \overline {EF} ,\hat B = \hat D\\\overline {BC} = \overline {DE} ,\widehat C = \hat E\end{array} \right.\)
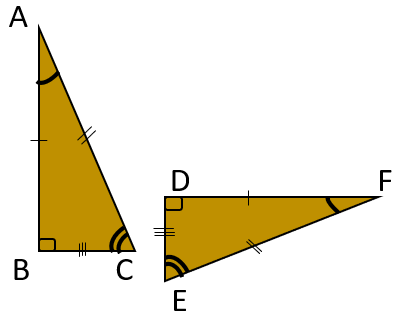
در شکل داده شده دو مثلث هم نهشتند تساوی اجزای متناظر را بنویسید.
\(A\mathop B\limits^\Delta C \cong M\mathop N\limits^\Delta Q \Rightarrow \left\{ \begin{array}{l}\overline {AB} = \overline {MN} ,\widehat A = \hat M\\\overline {AC} = \overline {QM} ,\widehat B = \widehat N\\\overline {BC} = \overline {QN} ,\widehat C = \widehat Q\end{array} \right.\)
دقت کنیم محیط یا مساحت دو شکل هم نهشت با هم برابرند ولی برعکس این جمله صحیح نیست.
یعنی اگر محیط یا مساحت دو شکل برابر باشد ممکن است آن دو شکل هم نهشت نباشند.
به این دو مثال دقت کنید.
مثال (الف) مساحت مربعی به ضلع ۴ و مستطیلی به ابعاد ۲ و ۸ با هم برابر است.ولی این دو شکل هم نهشت نیستند.
مثال (ب) محیط این لوزی و مربع هر دو برابر است ولی هم نهشت نیستند.
به کمک هم نهشتی دو مثلث و تساوی اجزاء آنها میتوان مقادیر مجهول را محاسبه نمود.
دو مثلث داده شده با تقارن محوری بر هم منطبق میشوند با توجه به اندازه های داده شده مقادیر مجهول را بیابید.
با توجه به تناظر بین اضلاع و زاویه ها داریم:
\(\begin{array}{l}3x = x + 8 \Rightarrow 2x = 8 \Rightarrow x = 4\\2y - 47 = y + 10 \Rightarrow y = 10 + 47 \Rightarrow y = 57\\2z - 4 = z + 11 \Rightarrow 2z - {\rm{z = 11 + 4}} \Rightarrow z = 15\end{array}\)
دو مثلث مقابل هم نهشتند محیط هر کدام چقدر است؟
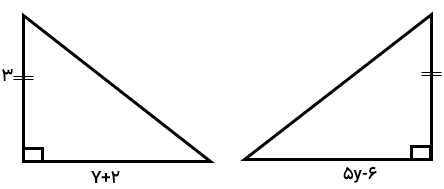
با توجه به تناظر اضلاع دو مثلث داریم
\(5y - 6 = y + 2 \Rightarrow 4y = 2 + 6 = 8 \Rightarrow y = \frac{8}{4} = 2\)
با جایگزین کردن مقدار ۲ = y در هر کدام از روابط بالا اندازه ی ضلع دوم مثلث را محاسبه می کنیم\(5 \times 2 - 6 = 10 - 6 = 4\) پس دو ضلع زاویه ی قائمه در این مثلث ۳ و ۴ هستند. به کمک رابطه ی فیثاغورس داریم:
\({x^2} = {4^2} + {3^2} = 16 + 9 = 25 \Rightarrow x = \sqrt {25} = 5\)
بنابراین محیط این دو مثلث برابر است با ۱۲ = ۳ + ۴ + ۵ = p
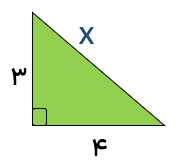
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
هم نهشتی مثلث ها
فصل 6 : مثلث
هم نهشتی مثلث ها
برای اینکه نشان دهیم دو مثلث هم نهشت هستند می توانیم از یکی از حالت های زیر استفاده کنیم و لازم نیست برابری تمامی اضلاع و زاویه ها بررسی گردد.
1- برابری سه ضلع ( ض ض ض )
2- برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
3- برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
4- برابری وتر و یک ضلع زاویه ی قائمه در مثلث قائم الزاويه ( و ض )
5- برابری وتر و یک زاویه ی تند از مثلث قائم الزاویه ( و ز )
تهیه کنندگان: شهریار ارم و ندا بهرامی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
برابری سه ضلع ( ض ض ض )
فصل 6 : مثلث
برابری سه ضلع ( ض ض ض )
اگر سه ضلع از مثلث اول با اضلاع مثلث دوم دو به دو با هم برابر باشند آن دو مثلث حتما هم نهشت هستند.
مثال
آیا دو مثلث ABC و DEF هم نهشتند؟
\(\left. \begin{array}{l}\overline {AB} = \overline {FD} = 2\\\overline {AC} = \overline {EF} = 4\\\overline {BC} = \overline {ED} = 5\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ض ض ض)
مثال
مثلث ABC متساوی الساقین و AM میانه ی وارد بر قاعده BC است . چرا دو مثلث ABM و ACMهم نهشتند؟
ابتدا توجه کنیم که میانه قاعده را به دو قسمت مساوی تقسیم می کند بنابراین داریم
\(\overline {AB} = \overline {AC} \) :زیرا مثلث متساوی الساقین است
\(\overline {BM} = \overline {CM} \) :زیرا AM میانه است
\(\overline {AM} = \overline {AM} \) :زیرا ضلع مشترک دو مثلث است
بنا به حالت (ض ض ض)\(\left. \begin{array}{l}\overline {AB} = \overline {AC} \\\overline {BM} = \overline {CM} \\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\)
نقاط M و N مرکز دو دایره هستند چرا دو مثلث AMN و BMN هم نهشتند؟
دقت کنیم در یک دایره شعاع ها با هم برابرند.
بنابراین :
چون شعاع دایره بزرگ هستند : AM = BM
\( \Rightarrow {\rm A}\mathop {\rm M}\limits^\Delta {\rm N} \cong {\rm B}\mathop {\rm M}\limits^\Delta {\rm N}\) چون شعاع دایره کوچک هستند : AN = BN
چون ضلع مشترک دو مثلث است : MN = M
تهیه کنندگان: شهرام ارم و ندا بهرامی
برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
فصل 6 : مثلث
برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
اگر دو ضلع از مثلث اول با دو ضلع از مثلث دوم برابر و زاویه ی بین آن دو ضلع در هر دو مثلث برابر باشد، آن دو مثلث حتما هم نهشت هستند.
مثال
آیا دو مثلث زیر هم نهشتند؟
بله، بنا به حالت ( ض ز ض)
\(\left. \begin{array}{l}\overline {AB} {\rm{ }} = {\rm{ }}F\overline D = 2\\\overline B {\rm{ }} = {\rm{ }}\bar D = 45^\circ \\\overline {BC} {\rm{ }} = {\rm{ }}\overline {ED} {\rm{ }} = 5\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ض ز ض)
مثال
مثلث ABC متساوی الساقین و AM نیمساز زاویه ی A است چرا دو مثلث ABM وACMهم نهشتند؟
ابتدا توجه کنیم که نیم ساز زاویه ی A را به دو قسمت مساوی تقسیم می کند بنابراین داریم:
زیرا مثلث متساوی الساقین است\(\overline {AB} = \overline {AC} \)
زیرا AM نیمساز \(\widehat A\) است \({\widehat A_1} = {\widehat A_2}\)
زیرا ضلع مشترک دو مثلث است\(\overline {AM} = \overline {AM} \)
\(\left. \begin{array}{l}\overline {AB} = \overline {AC} \\{\widehat A_1} = {\widehat A_2}\\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\) بنا به حالت (ض ز ض)
نقطه ی O مرکز دایره و AC و BD قطر های دایره هستند. چرا دو مثلث OAB و OCD هم نهشتند؟
دقت کنیم به زوایایی مانند دو زاویه ی ۱ و ۲ متقابل به راس می گویند و دو زاویه ی متقابل به راس همیشه با هم برابرند. بنابراین داریم:
\(\left. \begin{array}{l}\overline {OB} = \overline {OC} \\{\widehat O_1} = {\widehat O_2}\\\overline {OA} = \overline {OD} \end{array} \right\} \Rightarrow O\mathop A\limits^\Delta B \cong O\mathop D\limits^\Delta C\) بنا به حالت (ض ز ض)
دقت کنیم در این حالت (ض ز ض) زاویه ی مساوی باید حتما بین دو ضلع متناظر قرار داشته باشد.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
فصل 6 : مثلث
برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
اگر دو زاویه از مثلث اول با دو زاویه از مثلث دوم برابر و ضلع بین آن دو زاویه در هر دو مثلث برابر باشد، آن دو مثلث حتما هم نهشت هستند.
مثال : دو مثلث زیر هم نهشتند زیرا :
\(\left. \begin{array}{l}\widehat B = \widehat D = 45^\circ \\\overline {BC} = \overline {ED} = 5\\\widehat C = \widehat E = 20^\circ \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ز ض ز)
مثال
در مثلث ABC پاره خط AM نیمساز زاویه ی A و بر BC عمود است چرا دو مثلث ABM و ACMهم نهشتند؟
ابتدا توجه کنیم که نیم ساز AM زاویه A را به دو قسمت مساوی تقسیم می کند.و چون بر قاعده یBCعمود است زوایای M و M قائمه هستند.بنابراین داریم:
زیرا AM برBC عمود است \({\widehat M_1} = \widehat {{M_2}}\)
زیرا AMنیمساز A است. \(\widehat {{A_1}} = \widehat {{A_2}}\)
زیرا ضلع مشترک دو مثلث است.\(\overline {AM} = \overline {AM} \)
\(\left. \begin{array}{l}{\widehat M_1} = \widehat {{M_2}} = 90^\circ \\\widehat {{A_1}} = \widehat {{A_2}}\\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\)
مثال
نقطه ی M وسط پاره خط AB است چرا دو مثلث ACM و BDM هم نهشتند؟
\({\widehat M_1} = \widehat {{M_2}}\) : زیرا متقابل به راس هستند
\(\overline {AM} = \overline {MB} \) :زیرا M وسط پاره خط ABاست.
\(\left. \begin{array}{l}{\widehat M_1} = \widehat {{M_2}}\\\widehat A = \widehat B = 90^\circ \\\overline {AM} = \overline {MB} \end{array} \right\} \Rightarrow A\mathop C\limits^\Delta M \cong B\mathop D\limits^\Delta M\)
دقت کنیم اگر ضلع بین دو زاویهی مساوی نباشد دو مثلث هم نهشتند زیرا در صورت تساوی دو زاویه در دو مثلث ، زوایای سوم نیز با هم برابرند و به حالت سوم دو مثلث هم نهشت خواهند بود. برای درک بیشتر به مثال زیر دقت کنید.
در این دو مثلث دو زاویه مساوی وجود دارد بنابر این زاویه ی سوم در هر دو مثلث برابر است با:
پس زاویه سوم در هر دو مثلث ۷۰ درجه است و ضلع متناظر بین دو زاویه ی مساوی در دو مثلث دو زاویه ی ۷۰ و ۷۵ درجه قرار میگیرد و بنا به حالت سوم دو مثلث هم نهشتند.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
هم نهشتی مثلث های قائم الزاویه
فصل 6 : مثلث
هم نهشتی مثلث های قائم الزاویه
مثال
در شکل زیر وتر و یک ضلع از هر دو مثلث با هم برابرند با توجه به شکل های داده شده اندازه ی ضلع سوم در هر مثلث را محاسبه کنید و اندازه ی ضلع سوم را با هم مقایسه کنید.
اگر ضلع سوم را a در نظر بگیریم بنا به رابطه ی فیثاغورس در هر دو مثلث داریم:
\({a^2} = {(\sqrt 5 )^2} - {1^2} = 5 - 1 = 4 \to a = \sqrt 4 = 2\)
با مقایسه متوجه میشویم که اندازه ی ضلع سوم در هر دو مثلث ۲ واحد است. دقت کنیم که دو مثلث هم نهشتند.(به دلیل داشتن سه ضلع مساوی)
طبق مثال بالا برای مثلث های قائم الزاویه علاوه بر سه حالت قبل میتوان حالت هم نهشتی زیر را در نظر گرفت.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
برابری وتر و یک ضلع زاویه ی قائمه ( و ض )
فصل 6 : مثلث
برابری وتر و یک ضلع زاویه ی قائمه در مثلث قائم الزاويه ( و ض )
دقت کنیم این حالت فقط مخصوص مثلث های قائم الزاویه است.
مثال
با توجه به شکل داده شده چرا دو مثلث ABC و DBC هم نهشتند؟ ( طبق شکل\(\overline {AB} = \overline {DB} \) )
با توجه به این که دو مثلث قائم الزاویه هستند و وتر هر دوی آن ها BC است داریم:
\(\left. \begin{array}{l}\widehat A = \widehat D = 90^\circ \\\overline {BC} = \overline {BC} \\\overline {AB} = \overline {DB} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک ضلع)
مثال
مثلث ABC متساوی الساقین و AH ارتفاع آن است. چرا دو مثلث ABH وACH هم نهشتند؟
ابتدا توجه کنیم چون AH ارتفاع است پس دو مثلث ABH و ACH قائم الزاویه هستند و AB و AC در دو مثلث وتر هستند.
\(\overline {AH} \) :ضلع مشترک دو مثلث است
\(\left. \begin{array}{l}\widehat {{H_1}} = {\widehat H_2} = 90^\circ \\\overline {AB} = \overline {AC} \\\overline {AH} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک ضلع)
مثال
با توجه به اطلاعات داده شده برای هم نهشتی کدام مثلث ها دلایل کافی داریم؟
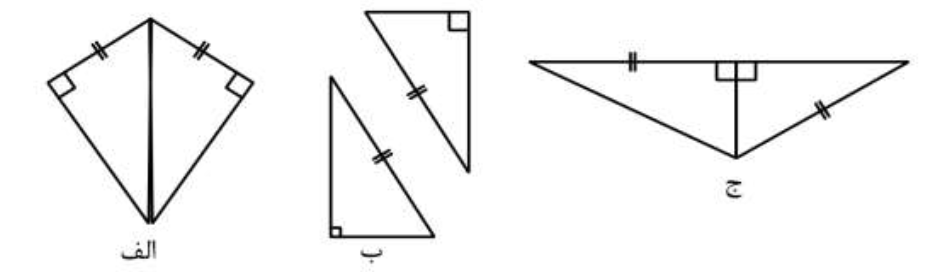
الف) دو مثلث وتر مشترک دارند و یک ضلع زاویه ی قائمه در هر دو مثلث با هم برابرند.
بنابراین به حالت وتر و یک ضلع که برای خلاصه تر شدن به صورت )و ض) نوشته می شود،هم نهشتند.
ب) وتر دو مثلث قائم الزاویه در هر دو برابر است ولی در مورد تساوی اضلاع دیگر اطلاعات مساله کافی نیست.
پس در این حالت دو مثلث هم نهشت نیستند.
ج) دو مثلث قائم الزاویه هستند و یک ضلع زاویهی قائمه در هر دو مشترک است ولی اضلاعی که با هم مساوی هستند و تساوی آنها با علامت مشخص شده در یکی از مثلثها وتر و در دیگری ضلع زاویه ی قائمه است. پس دو مثلث هم نهشت نیستند.
در شکل زیر وتر و یک زاویه ی تند از دو مثلث با هم برابرند با توجه به اندازه های داده شده اندازه ی a و b را در هر مثلث محاسبه کنید. پاسخ در مثلث قائم الزاویه دو زاویه تند متمم یکدیگرند( یعنی مجموع دو زاویه ی تند ۹۰ درجه است.) بنابراین برای محاسبه ی a یا b کافی است اندازه ی زاویه ی تند دیگر را از ۹۰ درجه کم کنیم. پس:
\(a = b = 90^\circ - 32^\circ = 58^\circ \)
دقت کنیم که دو مثلث هم نهشتند(به دلیل داشتن دو زاویه و ضلع بین آن ها)
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
برابری وتر و یک زاویه ی تند ( و ز )
فصل 6 : مثلث
برابری وتر و یک زاویه ی تند از مثلث قائم الزاویه ( و ز )
دقت کنیم این حالت هم مانند حالت قبل فقط مخصوص مثلث های قائم الزاویه است.
مثال
در شکل داده شده BC نیمساز زاویه ی B است چرا دو مثلث ABC و DBC هم نهشتند؟
با توجه به این که دو مثلث قائم الزاویه هستند و وتر هر دوی آن ها BC است داریم
\(\left. \begin{array}{l}\widehat A = \widehat D = 90^\circ \\\overline {BC} = \overline {BC} \\\widehat {{B_1}} = \widehat {{B_2}}\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک زاویه تند)
مثال
با توجه به اطلاعات داده شده برای هم نهشتی کدام مثلث ها دلایل کافی داریم؟
الف دو مثلث وتر مشترک دارند و یک زاویه ی تند در هر دو مثلث با هم برابرند. بنا بر این به حالت وتر و یک زاویه ی تند دو مثلث هم نهشتند.
ب یک ضلع و یک زاویه در هر دو مثلث برابرند ولی در مورد تساوی اجزای دیگر اطلاعات مساله کافی نیست، پس در این حالت دو مثلث هم نهشت نیستند.
ج دو مثلث قائم الزاویه هستند و و ترهای دو مثلث برابرند ولی اطلاعات سوال در مورد تساوی دیگر اجزاء کافی نیست.پس دو مثلث هم نهشت نیستند.
در شکل مقابل AB قطر دایره است چرا دو مثلث OAC و OBD هم نهشتند؟
دقت کنیم A و OB شعاع دایره و و ترهای این دو مثلث قائم الزاویه هستند پس برای نشان دادن هم نهشتی دو مثلث از حالتهای مخصوص مثلث قائم الزاویه با داشتن وتر مساوی استفاده میکنیم داریم:
\(\left. \begin{array}{l}\widehat C = \widehat D = 90^\circ \\\widehat {{O_1}} = \widehat {{O_2}}\\\overline {OA} = \overline {OB} \end{array} \right\} \Rightarrow O\mathop A\limits^\Delta C \cong O\mathop B\limits^\Delta D\) بنا به حالت (وتر و یک زاویه ی تند)
دو دایره ی داده شده هم مرکز هستند و چرا دو مثلث OAD و OBC هم نهشتند؟
دقت کنیم OA و OB شعاعهای دایره ی کوچک و OC و OD شعاع های دایره ی بزرگ هستند و دو زاویه ی o متقابل به راس هستند. بنابراین داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OD} \\\widehat {{O_1}} = \widehat {{O_2}}\\\overline {OB} = \overline {OA} \end{array} \right\} \Rightarrow O\mathop B\limits^\Delta C \cong O\mathop A\limits^\Delta D\) بنا به حالت (ض ز ض)
چهار ضلعی ABCD متوازی الاضلاع و AE و CF بر قاعده های آن عمودند.
الف) چرا دو مثلث ABE و CDF هم نهشتند؟
می دانیم در هر متوازی الاضلاع اضلاع و زاویه های رو به رو دو به دو با هم برابرند، از طرفی دو مثلث قائم الزاویه و AB و CD و ترهای آن هستند. پس داریم:
\(\overline {AB} = \overline {CD} \) : وتر
\(\widehat B = \widehat D\) :دو زاویه تند
\(\left. \begin{array}{l}\widehat E = \widehat F = 90^\circ \\\overline {AB} = \overline {CD} \\\widehat B = \widehat D\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta E \cong C\mathop D\limits^\Delta F\) بنا به حالت (وتر و یک زاویه تند)
ب( با توجه به قسمت الف و هم نهشتی دو مثلث تساوی های زیر را کامل کنید.
\(\begin{array}{l}\overline {AE} = ...{\rm{ }}\\\\\overline {FD} = ...{\rm{ }}\\\\{\widehat A_1} = ...\end{array}\)
\(\begin{array}{l}\overline {AE} = \overline {FC} \\\\\overline {FD} = \overline {BE} {\rm{ }}\\\\{\widehat A_1} = {\widehat C_1}\end{array}\)
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
تعریف توان
فصل 7 : توان و جذر
تعریف توان
عبارتی مانند ۲ × ۲ × ۲ × ۲ × 2 را در ریاضیات برای ساده تر شدن به صورت 25 می نویسیم و آن را چنین می خوانیم:
۲ به توان 5
در عبارت 25، ۲ را پایه و ۵ را توان می نامیم، درست شبیه همان کاری که در ساده کردن و خلاصه کردن جمع انجام می دادیم:
۲+۲+۲+۲+۲ = 2×5
نکاتی درباره توان
1) از توان به منظور مختصر نویسی ضرب های تکراری یک عدد استفاده می کنند.
2) به توان، «نما» و «قوّه» هم گفته می شود.
3) هر عدد به توان یک برابر خودش می شود:
\({a^1} = a\)
4) عدد یک به توان هر عددی برابر یک می شود:
\({1^{53}} = 1\)
5) هر عدد به توان صفر، ۱ می شود:
\({12^ \circ } = 1\)
6) عدد صفر به توان هر عدد مثبتی برابر صفر می شود:
\({ \circ ^{15}} = \circ \)
7) صفر به توان صفر تعریف نشده است:
\({ \circ ^ \circ } = \) تعریف نشده
مثال
حاصل عبارات زیر را بدست آورید.
\(\begin{array}{l}1)\,{10^ \circ }\;\;\;\;\;\;\;2){1^7}\;\;\;\;\;\;\;3){ \circ ^4}\;\;\;\;\;\;\;4){5^1}\\\\5){( - 6)^2}\,\,\,\,\,6) - {3^3}\,\,\,\,7){( - 2)^ \circ }\,\,\,\,\,\,8)( - 3) \times ( - 3) \times ( - 3)\\\\9){11^2}\,\,\,\,\,\,\,\,\,\,10){6^1}\,\,\,\,\,\,\,\,\,\,11){ \circ ^1}\,\,\,\,\,\,\,\,\,\,\,12){( - 2)^ \circ } \times {2^5}\end{array}\)
\(\begin{array}{l}1)\,{10^ \circ } = 1\;\;\;\;\;\;\;\\\\2){1^7} = 7\;\\\\3){ \circ ^4} = \; \circ \\\\4){5^1} = 5\\\\5){( - 6)^2} = \,( - 6) \times ( - 6) = 36\\\\6) - {3^3} = - (3 \times 3 \times 3) = - 27\\\\7){( - 2)^ \circ } = 1\\\,\,\\8)( - 3) \times ( - 3) \times ( - 3) = {( - 3)^2} = - 27\\\\9){11^2} = 11 \times 11 = 121\,\,\,\,\,\\\\10){6^1} = 6\\\\11){ \circ ^1} = \circ \\\\12){( - 2)^ \circ } \times {2^5} = 1 \times 2 \times 2 \times 2 \times 2 \times 2 = 32\end{array}\)
نقش پرانتز در اعداد توان دار
فصل 7 : توان و جذر
نقش پرانتز در اعداد توان دار
1) اگر عددی منفی داخل پرانتز به توان زوج رسید، حاصل عددی مثبت می شود:
\({( - 3)^2} = ( - 3) \times ( - 3) = + 9\)
2) اگر توان عددی منفی داخل پرانتز بود، پرانتز در توان رساندن عدد نقشی ندارد:
\(( - {3^2}) = - (3 \times 3) = - 9\)
3) اگر عددی منفی بدون پرانتز به توان برسد، حاصل عددی منفی می شود:
\( - {4^2} = - (4 \times 4) = - 16\)
4) اگر یک کسر داخل پرانتز به توان برسد، توان شامل صورت و مخرج (هر دو) می شود:
\({(\frac{2}{3})^3} = \frac{{2 \times 2 \times 2}}{{3 \times 3 \times 3}} = \frac{8}{{27}}\)
5) اگر کسری داخل پرانتز به توان گرفت یا توان در صورت یا مخرج کسر باشد، پرانتز هیچ نقشی در توان ندارد:
\(\begin{array}{l}(\frac{{{2^3}}}{5}) = \frac{{2 \times 2 \times 2}}{5} = \frac{8}{5}\\\\\frac{7}{{{3^3}}} = \frac{7}{{3 \times 3 \times 3}} = \frac{7}{{27}}\end{array}\)
6) اگر یک عبارت جبری داخل پرانتز به توان برسد، توان شامل تک تک جمله های عبارت می شود:
\({(2ab)^3} = {2^3}{a^3}{b^3} = 8{a^3}{b^3}\)
7) اگر جمله ای از یک عبارت جبری توان نداشت، توانش ۱ می باشد:
\(5{a^2}b{x^8} = 5{a^2}{b^1}{x^8}\)
مثال
حاصل عبارات زیر را بدست آورید.
\(\begin{array}{l}1)\,{( - 1)^4}\;\;\;\;\;\;\;2){( - 1)^3}\;\;\;\;\;\;\;3)( - {3^4})\;\;\;\;\;\;\;4) - {5^2}\\\\5)\frac{4}{{{3^2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6)\frac{{{{( - 4)}^2}}}{{{4^2}}}\,\,\,\,\,\,\,7){( - \frac{2}{5})^2}\,\,\,\,\,\,\,\,\,\,8){(\frac{a}{b})^3}\end{array}\)
\(\begin{array}{l}1)\,{( - 1)^4} = 1\\\\2){( - 1)^3} = - 1\\\\3)( - {3^4}) = - (3 \times 3 \times 3 \times 3) = - 81\\\\4) - {5^2} = - (5 \times 5) = - 25\\\\5)\frac{4}{{{3^2}}} = \frac{4}{{3 \times 3}} = \frac{4}{9}\\\\6)\frac{{{{( - 4)}^2}}}{{{4^2}}} = \frac{{( - 4) \times ( - 4)}}{{4 \times 4}} = \frac{{16}}{{16}} = 1\\\\7){( - \frac{2}{5})^2} = ( - \frac{2}{5}) \times ( - \frac{2}{5}) = \frac{4}{{25}}\\\\8){(\frac{a}{b})^3} = \frac{a}{b} \times \frac{a}{b} \times \frac{a}{b} = \frac{{a \times a \times a}}{{b \times b \times b}} = \frac{{{a^3}}}{{{b^3}}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
محاسبه عبارت توان دار
فصل 7 : توان و جذر
محاسبه عبارت توان دار
با توجه به درس توان، ترتیب انجام دادن عملیات مختلف ریاضی به صورت زیر انجام می شود:
۱) پرانتز
2) توان
3) ضرب و تقسیم
۴) جمع و تفریق
به عنوان مثال:
\(\frac{{{4^3} \times 4 + 9 - 6}}{{{5^2} + {2^3}}} = \frac{{64 \times 4 + 3}}{{25 + 8}} = \frac{{259}}{{33}}\)
گسترده توانی یک عدد
در نوشتن گسترده توانی هر عدد، ارزش مکانی رقم ها را به صورت توانی از ۱۰ می نویسیم:
\(\begin{array}{l}5062 = 5000 + 60 + 2\\\,\,\,\,\,\,\,\,\,\,\, = 5 \times {10^3} + \circ \times {10^2} + 6 \times {10^1} + 2 \times {10^ \circ }\end{array}\)
مثال
حاصل عبارت زیر را به دست آورید.
\(\frac{{{5^3} - {3^3}}}{{{5^3} + {3^3}}} = \)
\(\frac{{{5^3} - {3^3}}}{{{5^3} + {3^3}}} = \frac{{125 - 27}}{{125 + 27}} = \frac{{98}}{{152}} = \frac{{49}}{{76}}\)
مثال
.گسترده توانی عددهای 58906 و 40200 را بنویسید
\(\begin{array}{l}58906 = 50000 + 8000 + 900 + 6\\\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 5 \times {10^4} + 8 \times {10^3} + 9 \times {10^2} + \circ \times {10^1} + 6 \times {10^ \circ }\\\\40200 = 40000 + 200\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 4 \times {10^4} + \circ \times {10^3} + 2 \times {10^2} + \circ \times {10^1} + \circ \times {10^ \circ }\\\end{array}\)
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
ساده کردن عبارت های توان دار
فصل 7 : توان و جذر
ساده کردن عبارت های توان دار
۱) در ضرب عددهای توان دار با پایه های مساوی یکی از پایه ها را نوشته و توان ها را جمع می کنیم:
\({\left( { - 3} \right)^2} \times {\left( { - 3} \right)^4} = {\left( { - 3} \right)^{2 + 4}} = {\left( { - 3} \right)^6}\)
2) در ضرب عددهای توان دار با توان های مساوی، پایه ها را در هم ضرب و یکی از توان ها را می نویسیم:
\({5^4} \times {\left( { - 3} \right)^4} = {\left( {5 \times ( - 3)} \right)^4} = {\left( { - 15} \right)^4}\)
3) اگر ظاهر پایه ها مثل هم نبود، مثلاً یکی عدد و دیگری کسر بود، سعی می کنیم آنها به یک شکل تبدیل کنیم:
\(\begin{array}{l}{(\frac{1}{2})^3} \times {(0/5)^6} = ?\\0/5 = \frac{5}{{10}} = \frac{1}{2}\\{(\frac{1}{2})^3} \times {(0/5)^6} = {(\frac{1}{2})^3} \times {(\frac{1}{2})^6} = {(\frac{1}{2})^{3 + 6}} = {(\frac{1}{2})^9}\end{array}\)
4) یک عدد توان دار را در صورت نیاز می توان به صورت ضرب دو یا چند عدد توان دار تبدیل کرد:
\(\begin{array}{l}{3^7} = {3^2} \times 3 \times {3^4}\\{15^4} = {3^4} \times {5^4}\end{array}\)
این خواص کمک به حل بسیاری از سوالات اعداد توان دار می نماید.
مثال
اگر \({2^{10}} = 1024\) باشد، حاصل 212 را به دست آورید.
\({2^{12}} = {2^{10}} \times {2^2} = 1024 \times 4 = 4096\)
مثال
باز شده عدد توان دار زیر را بنویسید.
\({12^7} = ?\)
\({12^7} = {(2 \times 6)^7} = {2^7} \times {6^7}\)
مثال
عبارت توان دار زیر را ساده کنید.
\({5^2} \times {5^7} \times {7^9} = ?\)
\(\begin{array}{l}\underline {{5^2} \times {5^7}} \times {7^9} = {5^{2 + 7}} \times {7^9} = {5^9} \times {7^9} = {(5 \times 7)^9}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {35^9}\end{array}\)
پیش بینی ارقام یک عدد توان دار
اگر \({4^5} = 1024\) باشد، عدد \({4^{10}}\) چند رقمی است ؟
\({4^{10}} = {4^5} \times {4^5}\)
اگر \({4^5}\) را ۱۰۰۰ فرض کنیم، پس داریم:
\(1000 \times 1000 = 1,000,000\)
در نتیجه \({4^{10}}\) هفت رقمی خواهد بود.
1 استثنای تفریق اعداد توان دار:
\(\begin{array}{l}{10^2} - {6^2} = {4^3}\\{21^2} - {15^2} = {6^3}\end{array}\)
2 استثنای جمع اعداد توان دار:
\({3^9} + {3^9} + {3^9} = {3^9} \times 3 = {3^{10}}\)
محاسبه عبارت توان دار به کمک مقدار داده شده
مثال
اگر \({2^a} = 7\) باشد، مقدار \({2^{a + 1}}\) را بدست آورید.
\({2^{a + 1}} = {2^a} \times {2^1} = 7 \times 2 = 14\)
مثال
حاصل عبارات توان دار زیر را حل کنید.
\(\begin{array}{l}1)\, - {(1 - 2(1 - 2(1 - 2(1 - {2^{ - 1}}))))^{ - 1}}\\\\2)\,\frac{{{4^{a + 2}} - {4^{a + 1}} - {4^a}}}{{{2^a} + {2^a} + {2^a} + {2^a}}}\\\\3)\,\frac{{{2^{101}} + {2^{100}} + {2^{99}} \cdots + {2^{60}}}}{{{2^{51}} + {2^{100}} + {2^{99}} \cdots + {2^{10}}}}\\\\4)\,\frac{{{3^{2a + 2}} \div {3^{2a - 2}}}}{{{9^{2b + 2}} \times {9^{ - 2b}}}}\end{array}\)
1) فقط به اولویت عملیاتی دقت کنید:
\(\begin{array}{l} - {(1 - 2(1 - 2(1 - 2(1 - {2^{ - 1}}))))^{ - 1}}\mathop = \limits^{{2^{ - 1}} = \frac{1}{2}} \\\\ - {(1 - 2(1 - 2(1 - 2(1 - \frac{1}{2}))))^{ - 1}} = \\\\ - {(1 - 2(1 - 2(1 - 2(\frac{1}{2}))))^{ - 1}} = \\\\ - {(1 - 2(1 - 2(1 - 0)))^{ - 1}} = \\\\ - {(1 - 2(1 - 2))^{ - 1}} = \\\\ - {(1 - 2( - 1))^{ - 1}} = - {(1 + 2)^{ - 1}} = - {(3)^{ - 1}} = - \frac{1}{3}\end{array}\)
2)
\(\begin{array}{l}\frac{{{4^{a + 2}} - {4^{a + 1}} - {4^a}}}{{{2^a} + {2^a} + {2^a} + {2^a}}} = \frac{{{4^a}({4^2} - 4 - 1)}}{{{2^a} \times 4}} = \\\\\frac{{{4^a}}}{{{2^a}}} \times \frac{{11}}{4} = {(\frac{4}{2})^a} \times \frac{{11}}{4} = {2^a} \times \frac{{11}}{4}\end{array}\)
3)
\(\begin{array}{l}\,\frac{{{2^{101}} + {2^{100}} + {2^{99}} \cdots + {2^{60}}}}{{{2^{61}} + {2^{60}} + {2^{59}} \cdots + {2^{10}}}} = \\\\\frac{{{2^{60}}({2^{51}} + {2^{50}} + {2^{49}} \cdots + 2 + 1)}}{{{2^{10}}({2^{51}} + {2^{50}} + {2^{49}} \cdots + 2 + 1)}} = \frac{{{2^{60}}}}{{{2^{10}}}} = {2^{60 - 10}} = {2^{50}}\\\end{array}\)
4)
\(\,\frac{{{3^{2a + 2}} \div {3^{2a - 2}}}}{{{9^{2b + 2}} \times {9^{ - 2b}}}} = \frac{{{3^{(2a + 2) - (2a - 2)}}}}{{{9^{(2b + 2 + ( - 2b))}}}} = \frac{{{3^4}}}{{{9^2}}} = \frac{{81}}{{81}} = 1\)
جذر(ریشه دوم)
فصل 7 : توان و جذر
جذر(ریشه دوم)
هر گاه عددی در خودش ضرب شود، این حاصل را مجذور و به عددی که در خوش ضرب شده جذر می گوییم. هر عدد مثبت دارای دو ریشه، یکی مثبت و دیگری منفی می باش . مانند عدد ۲۵ که دو ریشه ۵+ و ۵- را دارد.
1 به ریشه دوم مثبت هر عدد جذر آن عدد گفته می شود.
2 علامت جذر \(\sqrt {} \) است .
3 جذر هر عدد برابر است با دو عدد که قرینه یکدیگرند.
4 به جذر یک عدد ریشه دوم آن نیز گفته می شود.
5 اعداد منفی جذر ندارند. زیرا حاصل ضرب هیچ عددی در خوش، منفی نمی شود. عدد صفر تنها یک ریشه دارد که آن خود عدد صفر است.
انواع جذر
1- جذر کامل:
اعداد طبیعی که جذر کامل دارند، یعنی جذر آنها یک عدد طبیعی می شود را مجذور کامل گویند؛ مانند 1، 4، 9، 16، 25 و … . برای رسیدن به جذر کامل از خود سوال کنید چه عددی در خوش ضرب شده که عدد زیر رادیکال را تشکیل داده است؟ مانند:
\(\sqrt {49} = 7\)
2- جذر تقریبی:
جذرهایی که یک عدد اعشاری شوند. برای رسیدن به جذر تقریبی یک عدد، ابتدا باید معلوم کنید که عدد زیر رادیکال شما بین کدام دو عدد صحیح قرار گرفته است؛ مانند \(\sqrt {18} \) که بین دو رایکال \(\sqrt {16} \) و \(\sqrt {25} \) قرار گرفته یعنی \(\sqrt {16} < \sqrt {18} < \sqrt {25} \) بین دو عدد ۴ و 5 قرار گرفته است. این فاصله را نصف کرده به توان ۲ برسانید.
می توانید اگر به عدد کوچکتر نزدیک بود، 1/0 - 1/0 به عدد کوچکتر اضافه کنید تا به حدود جذر مورد نظر برسید و اگر به عدد بزرگتر نزدیک بود، 1/0 - 1/0 از عدد بزرگتر کم کنید تا به حدود جذر مورد نظر برسید.
پس داریم:
\(\sqrt {18} \simeq 4/2\)
مثال
حاصل عبارت هایی که جذر کامل دارند را بنویسید.
\(\begin{array}{l}1)\,\sqrt {49} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\sqrt {0/25} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3)\,\sqrt {8/1} \\\\4)\,\sqrt {8 \times 2} \,\,\,\,\,\,\,\,\,\,\,5)\,\sqrt 3 \times \sqrt {27} \,\,\,\,\,\,\,\,\,\,\,\,6)\,\sqrt 1 \\\\7)\sqrt {125} \,\,\,\,\,\,\,\,\,\,\,\,\,\,8)\sqrt {169} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9)\,\sqrt {\frac{{10}}{{0/1}}} \end{array}\)
\(\begin{array}{l}1)\,\sqrt {49} = 7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\sqrt {0/25} = 0/5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\3)\,\sqrt {8/1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4)\,\sqrt {8 \times 2} \, = \sqrt {16} = 4\\\\5)\,\sqrt 3 \times \sqrt {27} = \sqrt {3 \times 27} = \sqrt {81} = 9\\\\6)\,\sqrt {1\,} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7)\sqrt {125} \,\\\\8)\sqrt {169} = 13\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9)\,\sqrt {\frac{{10}}{{0/1}}} = \sqrt {10 \times 10} = 10\end{array}\)
مثال
حاصل عبارت زیر را حساب کنید.
\(\sqrt {\sqrt {\sqrt {\sqrt {{{81}^2}} } } } \)
\(\sqrt {\sqrt {\sqrt {\sqrt {{{81}^2}} } } } = \sqrt {\sqrt {\sqrt {81} } } = \sqrt {\sqrt 9 } = \sqrt 3 \)
مثال
حاصل عبارات زیر را بدست آورید.
\(\begin{array}{l}1)\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {\sqrt {2\sqrt 4 } } } } } } } } \\\\2)\sqrt {\frac{{25}}{{16}}} + \sqrt {\frac{9}{{25}}} - \sqrt {\frac{{16}}{9}} \end{array}\)
\(\begin{array}{l}1)\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt 4 } } } } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt 4 } } } } } } = \sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } } = \\\sqrt {2\sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } } = \sqrt {2\sqrt {2\sqrt {2\sqrt {2 \times 2} } } } = \\\sqrt {2\sqrt {2\sqrt {2 \times 2} } } = \sqrt {2\sqrt {2 \times 2} } = \sqrt {2 \times 2} = 2\\\\2)\sqrt {\frac{{25}}{{16}}} + \sqrt {\frac{9}{{25}}} - \sqrt {\frac{{16}}{9}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} + \frac{{\sqrt 9 }}{{\sqrt {25} }} - \frac{{\sqrt {16} }}{{\sqrt 9 }} = \\\frac{5}{4} + \frac{3}{5} - \frac{4}{3} = \frac{{75 + 36 - 80}}{{60}} = \frac{{31}}{{60}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
دسته بندی داده ها
فصل 8 : آمار و احتمال
علم آمار
علم جمع آوری سازماندهی تجزیه و تحلیل و تفسیر اطلاعات را علم آمار می گوییم.
داده
به اطلاعات عددی جمع آوری شده داده گفته میشود.
جدول داده ها
برای این که اطلاعات عددی دادهها به دست آمده راحت تر مورد استفاده قرار گیرند، آنها را درون یک جدول منظم قرار میدهیم که به آن جدول داده ها گفته میشود.
چوب خط(خط و نشان)
برای راحتی و سرعت عمل جمع آوری اطلاعات در هر طبقه به ازای هر عدد یک چوب خط میگذاریم پس از چهار چوب خط چوب خط پنجم را روی آن می کشیم.
فراوانی
به تعداد چوب خط های هر دسته (طبقه) فراوانی آن دسته گفته میشود.
نمودارهای آماری
برای آن که بتوان به راحتی داده های آماری را واضح و روشن مورد بررسی قرار داد و تصمیم گیری کرد، هر یک از جدول های آماری را به وسیله نمودارهایی معرفی می کنیم که به آن ها نمودارهای آماری گفته میشود.
انواع نمودار های آماری
نمودار میله ای یا ستونی
برای مقایسه تعداد یا مقادیر واقعی استفاده میشود.
میزان علاقمندی دانش آموزان یک کلاس به رشته های ورزشی مختلف.
نمودار خط شکسته
برای نشان دادن تغییرات داده ها در مدت مشخص استفاده می شود.
نمودار میانگین نمرات درس ریاضی دانش آموزان یک کلاس در شش ماهه اول سال تحصیلی.
نمودار دایره ای
برای نمایش تعداد داده های هر بخش به نسبت کل استفاده می شود.
نمودار نسبت گروه های مختلف خونی دانش آموزان یک مدرسه.
نمودار تصویری
برای داده های بزرگ و تقریبی استفاده میشود.
نمودار برداشت گندم در چهار استان به صورت تقریبی.
تهیه کنندگان:سمیه انصاری- عبدالهادی آرامی-عبدالله بهزادی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
دامنه تغییرات و حدود دسته
فصل 8 : آمار و احتمال
دامنه تغییرات
به اختلاف بیشترین داده و کمترین ،داده دامنه تغییرات گفته میشود.
کوچک ترین داده - بزرگترین داده = دامنه تغییرات
طول دسته (حدود دسته)
به حاصل تقسیم دامنه تغییرات بر تعداد دسته ها طول دسته گفته می شود.
مثال
بین نمرات درس ریاضی دانش آموزان یک کلاس کمترین نمره ۴ و بیشترین نمره ۱۹ بوده است.
الف) دامنه تغییرات را به دست آورید.
۱۵ = ۴ – ۱۹ = کوچکترین داده - بزرگترین داده = دامنه تغییرات
ب) حدود دسته ها را تعیین کنید.
\(4 \le x < 7\left( {4 + 3 = 7} \right)\) :دسته اول
\(7 \le x < 10\) :دسته دوم
\(10 \le x < 13\) :دسته سوم
\(13 \le x < 16\) :دسته چهارم
:\(16 \le x \le 19\) دسته پنجم
در هر دسته عدد کوچکتر متعلق به خود دسته میباشد ولی عدد بزرگتر متعلق به آن دسته نیست، بجز دسته آخر.
تهیه کنندگان:سمیه انصاری- عبدالهادی آرامی-عبدالله بهزادی
میانگین داده ها
فصل 8 : آمار و احتمال
میانگین
میانگین هر تعداد از داده های آماری از تقسیم مجموع داده ها بر تعداد آن ها به دست می آید.
(\(\overline x \) میانگین و s مجموع داده ها و n تعداد داده ها ) \(\overline x = \frac{s}{n}\)
مثال
نمرات چهار درس امیرحسین ۱۸ ،۲۰، ۱۴ و ۱۷ است میانگین نمرات او را به دست آورید.
\(\overline x = \frac{s}{n} = \frac{{18 + 20 + 14 + 17}}{4} = 17/25\)
مثال
میانگین ۶ داده آماری برابر ۱۲ میباشد. اگر اعداد ۱۵ و ۱۷ را به این اعداد اضافه کنیم، میانگین جدید را حساب کنید.
\(12 \times 6 = 72\) =مجموع \( \to \) تعداد×میانگین=مجموع
مجموع جدید=\(72 + 15 + 17 = 104\)
تعداد جدید=\(6 + 2 = 8\)
میانگین جدید=\(\frac{{104}}{8} = 13\)
اگر از بین داده یک عدد کمتر از میانگین را حذف کنیم میانگین جدید بیشتر می شود و برعکس اگر داده بیشتر از میانگین باشد میانگین جدید کمتر میشود.
مثال
میانگین نمرات یک دانش آموز ۱۷/۵ میباشد. اگر نمره ۱۹ را از بین نمرات او حذف کنیم،میانگین جدید بیشتر میشود یا کمتر؟ چرا؟
میانگین کمتر میشود زیرا نمره ۱۹ از میانگین بیشتر میباشد.
اگر همه داده ها با مقدار ثابتی جمع یا تفریق ،شوند میانگین نیز با همان مقدار ثابت جمع یا تفریق می شود.
مثال
میانگین نمرات یک دانش آموز ۱۸ میباشد. اگر از همه نمرات او ۱/۵ نمره کم کنیم، میانگین نمرات او چقدر میشود؟
از میانگین نیز ۱/۵ نمره کم میشود.
\(\overline x = 18 - 1/5 = 16/5\)
اگر همه داده ها در مقدار ثابتی ضرب یا تقسیم شوند، آن گاه میانگین نیز در همان مقدار ثابت ضرب یا تقسیم میشود.
میانگین در جدول آماری
ابتدا یک ستون به عنوان مرکز دسته متوسط دسته) ایجاد می کنیم که مرکز هر دسته را با استفاده از رابطه زیر محاسبه میکنیم.
در نهایت اگر مجموع اعداد ستون )فراوانی ×متوسط( را بر مجموع فراوانی ها تقسیم کنیم، میانگین تقریبی به دست می آید.
مثال
جدول زیر را کامل کرده و میانگین را به دست آورید.
تهیه کنندگان:سمیه انصاری- عبدالهادی آرامی-عبدالله بهزادی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
احتمال یا اندازه گیری شانس
فصل 8 : آمار و احتمال
پیشامد
به اتفاقی گفته میشود که ممکن است رخ بدهد یا رخ ندهد. مثل پیشامد رو آمدن در پرتاب سکه
احتمال
به نسبت تعداد حالت های مطلوب به تعداد کل حالتهای ممکن برای یک پیشامد، احتمال گفته میشود.
مثال
در یک کیسه ۵ مهره ،سفید ۴ مهره قرمز و ۳ مهره سبز وجود دارد،یک مهره به تصادف از این کیسه خارج میکنیم احتمال این که این مهره قرمز باشد چقدر است؟
تعداد حالت های مطلوب _ تعداد مهره های قرمز = ۴
تعداد حالتهای ممکن _ تعداد کل مهره ها= ۱۲
پیشامد قطعی (حتمی)
پیشامدی که به طور حتم رخ بدهد، احتمال آن یک است؛مانند احتمال کمتر از ۷ آمدن در پرتاب تاس.
پیشامد غیر ممکن
پیشامدی که اصلا رخ ندهد احتمال آن مساوی صفر است. مانند احتمال ظاهر شدن عدد ۸ در پرتاب تاس.
احتمال رخ دادن هر پیشامد عددی از صفر تا یک است یعنی \(0 \le P(A) \le 1\) است.
مثال
وقتی تاسی را پرتاب میکنیم، احتمال اینکه عددی فرد بیاید چند است؟
حالت های ممکن={ ۱, ۲,۳,۴,۵,۶}=۶
۳={۱,۳,۵}=حالت های مطلوب
مجموع احتمال های رخ دادن و رخ ندادن یک پیشامد برابر یک است و به کمک احتمال رخ دادن یک پیشامد می توان احتمال رخ ندادن آن را محاسبه کرد
احتمال رخ دادن – ۱ = احتمال رخ ندادن
مثال
احتمال برخورد یک تیر به هدف \(\frac{1}{2}\)میباشد. احتمال برخورد نکردن تیر به هدف چقدر است؟
\(1 - \frac{2}{9} = \frac{{9 - 2}}{9} = \frac{7}{9}\)
تهیه کنندگان:سمیه انصاری- عبدالهادی آرامی-عبدالله بهزادی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
بررسی حالت های ممکن در احتمال
فصل 8 : آمار و احتمال
بررسی حالت های ممکن در احتمال
برای محاسبه هر نوع احتمال در یک پیشامد ما نیاز به تعداد کل حالت - های ممکن پیشامد داریم که برای به دست آوردن کل حالتهای ممکن میتوان از جدول نظام دار یا نمودار درختی استفاده کرد.
مثال
یک سکه را دوبار پرتاب میکنیم حالتهای ممکن را بنویسید.
برای به دست آوردن حالت های ممکن میتوان از نمودار درختی استفاده کرد. در نتیجه تعداد کل حالت های ممکن ۴ حالت می باشد.
(رو-رو)،(رو-پشت)،(پشت،رو)،(پشت-پشت)
مثال
دو تاس را پرتاب می.کنیم با استفاده از جدول نظام دار تعداد کل حالت های ممکن را به دست آورید.
با هر شماره از تاس اول ممکن است ۶ شماره برای تاس دوم بیاید.
بنابراین برای پرتاب دو تاس ۳۶ حالت ممکن وجود دارد
تهیه کنندگان:سمیه انصاری- عبدالهادی آرامی-عبدالله بهزادی
خط و دایره
فصل 9 : دایره
دایره
مکان هندسی تمام نقاطی از صفحه است که از یک نقطه به نام مرکز دایره به یک فاصله است. این فاصله شعاع دایره نامیده میشود.
فاصله یک نقطه از یک خط کوتاه ترین فاصله طول پاره خطی است که از آن نقطه بر خط عمود می شود.
وضعیت خط و دایره
۱) خط خارج از دایره است.
2)\(r < OH\)
(3خط و دایره هیچ نقطه مشترکی ندارند.
1) خط بر دایره مماس است.
2)\(r = OH\)
3)خط و دایره یک نقطه مشترک دارند.
۱) خط از داخل دایره میگذرد.
2)\(OH < r\)
۳) خط و دایره دو نقطه مشترک دارند
۱ شعاع دایره در نقطه تماس بر خط مماس عمود است.
2 وتر ،دایره پاره خطی است که دو سر یک کمان را به هم وصل می کند.
3بزرگترین وتر،دایره قطر دایره است که از مرکز آن می گذرد و دایره را به دو کمان مساوی ۱۸۰ درجه تقسیم می کند. \(\overline {CD} \)وتر = قطر دایره
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تعیین مرکز دایره
فصل 9 : دایره
تعیین مرکز دایره
دو وتر غیر موازی رسم کرده و سپس عمود منصف هر دو وتر را رسم می کنیم. محل برخورد دو عمود منصف مرکز دایره است (O مرکز دایره است(
نشان دهید اگر خطی از مرکز دایره بر وتر عمود ،شود آن را به دو قسمت مساوی تقسیم می کند. (O مرکز دایره است(.
فرض مسئله(شعاع دایره) OA = OB
ضلع مشترک OH = OH
به حالت وتر و یک ضلع داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OB} \\\\\overline {OH} = \overline {OH} \end{array} \right\} \Rightarrow A\mathop O\limits^\Delta H \cong B\mathop O\limits^\Delta H\)
بنابراین\( \leftarrow \)AH = HB
در نتیجه اگر خطی از مرکز دایره بر وتر عمود شود آن را به دو قسمت مساوی تقسیم می کند.
\(\widehat {{H_1}} = \widehat {{H_2}} = 90 \to \overline {AH} = \overline {HB} \)
نشان دهید اگر خطی از مرکز دایره به وسط وتر رسم کنیم بر آن وتر عمود می شود (O مرکز دایره است(.
\(\widehat {{M_1}} = \widehat {{M_2}} = 90^\circ \)
شعاع دایرهOA = OB
فرض مسئلهAM = MB
ضلع مشترک OM = OM
بنا به حالت (ض ض ض)داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OB} \\\overline {OM} = \overline {OM} \\\overline {AM} = \overline {MB} \end{array} \right\} \Rightarrow A\mathop O\limits^\Delta M \cong B\mathop O\limits^\Delta M\)
بنابراین\({M_1} = {M_2} = 90 \leftarrow \)
در نتیجه اگر خطی از مرکز دایره به وسط یک وتر رسم کنیم بر آن وتر عمود میشود.
\(\overline {AM} = \overline {MB} \to {M_1} = {M_2} = 90\)
فاصله مرکز دایره از وتر طول پاره خطی است که از مرکز دایره بر وتر عمود شده وآن را نصف میکند.
از هر نقطه خارج از دایره دو مماس میتوان بر دایره رسم کرد که طول هر دو مماس با هم برابراست.
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم
جزوه جامع علوم تجربی هشتم
جزوه جامع مطالعات اجتماعی هشتم
جزوه جامع عربی هشتم
جزوه جامع فارسی هشتم
جزوه جامع نگارش هشتم
جزوه جامع زبان انگلیسی هشتم
جزوه جامع کتاب کار انگلیسی هشتم
جزوه جامع پیام های آسمانی هشتم
جزوه جامع آموزش قرآن هشتم
جزوه جامع کار و فناوری هشتم
جزوه جامع تفکر و سبک زندگی هشتم
زاویه مرکزی
فصل 9 : دایره
زاویه مرکزی
زاویه مرکزی زاویه ای است که رأس آن روی مرکز دایره و اضلاع آن شعاع های دایره هستند.اندازه زاویه مرکزی برابر است با اندازه کمان روبروی آن.\(\widehat {{O_1}} = AB\)
یک رابطه مهم:
مثال
اگر \(\overline {OB} = 1cm\) باشد طول کمان AB چقدر است؟
محیط دایره: \( \Rightarrow 2\pi r = 1 \times 2 \times \pi = 2\pi \)
\(\frac{{60}}{{360}} = \frac{x}{{\pi 2}} \to x = \frac{{60 \times 2\pi }}{{360}} = \frac{\pi }{3}\)
مثال
اگر \(\overline {OD} = 2cm\) ،باشد طول کمان CD چقدر است؟
محیط دایره: \( \Rightarrow 2 \times 2 \times \pi = 4\pi \)
\(\frac{{60}}{{360}} = \frac{x}{{\pi 4}} \to x = \frac{{60 \times 4\pi }}{{360}} = \frac{{2\pi }}{3}\)
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
طریقه رسم اشکال مختلف
فصل 9 : دایره
طریقه رسم پنج ضلعی منتظم
ابتدا ۳۶۰ را تقسیم بر ۵ کرده و اندازه زاویه مرکزی ۵ضلعی منتظم را به دست می آوریم. \(\left( {\frac{{360}}{5} = 72} \right)\) حال زاویه مرکزی ۷۲ درجه را رسم می کنیم دهانه پرگار را به اندازه کمان ۷۲ درجه باز کرده و سوزن پرگار را روی یکی از نقاط برخورد اضلاع زاویه با محیط دایره قرار داده و کمان های پی در پی میزنیم حال نقاط ایجاد شده را به هم وصل می کنیم.
طریقه رسم شش ضلعی منتظم
دهانه پرگار را به اندازه شعاع موردنظر باز کرده و از یک نقطه دلخواه روی محیط دایره کمان های پی در پی میزنیم بدین ترتیب دایره به ۶ کمان مساوی تقسیم میشود. حال نقاط به دست آمده را به هم وصل می کنیم.
طریقه رسم سه ضلعی منتظم
مانند آنچه برای شش ضلعی منتظم بود عمل می کنیم ولی نقاط به دست آمده را یکی در میان به هم وصل میکنیم.
طریقه رسم هشت ضلعی منتظم
ابتدا ۳۶۰ را بر ۸ تقسیم کرده و اندازه زاویه مرکزی۸ ضلعی منتظم را به دست می آوریم\(\left( {\frac{{360}}{8} = 45} \right)\) دهانه پرگار را به اندازه کمان ۴۵درجه باز کرده و از یک نقطه دلخواه کمان های پی در پی میزنیم حال نقاط ایجاد شده را به هم وصل می کنیم.
1 برای رسم هر 11 ضلعی منتظم مشابه روش های بالا عمل میکنیم
2 وترهای نظیر کمانهای مساوی با یکدیگر برابر میباشند.\(AB = CD = \overline {AB} = \overline {CD} \)
3کمان های نظیر وترهای مساوی با یکدیگر برابر هستند.\(\overline {AB} = \overline {CD} = AB = CD\)
4قطر دایره دایره را به دو کمان ۱۸۰ درجه تقسیم میکند.
5 محیط ،دایره برابر ۳۶۰ درجه است.
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
زاویه محاطی
فصل 9 : دایره
زاویه محاطی
زاویه محاطی به زاویه ای گفته میشود که رأس آن روی محیط دایره و اضلاع آن وترهای دایره باشند.
با توجه به مرکز دایره و وضعیت قرار گرفتن وترها نسبت به مرکز دایره سه نوع زاویه محاطی می توانیم ایجاد کنیم.
اندازه زاویه محاطی نصف کمان روبروی آن است.\(\widehat A = \frac{{\widehat {BC}}}{2}\)
مثال
در شکل مقابل اندازه زاویه های خواسته شده را به دست آورید.
\(\begin{array}{l}\widehat A = ?\\\widehat {{O_1}} = ?\end{array}\)
\(\begin{array}{l}\widehat A = 40^\circ \\\widehat {{O_1}} = 80^\circ \end{array}\)
مثال
در شکل مقابل اندازه زاویه های خواسته شده را به دست آورید.
\(\begin{array}{l}\widehat {{O_1}} = ?\\AB = ?\\BC = ?\end{array}\)
\(\begin{array}{l}\widehat {{O_1}} = 100^\circ \\AB = 130^\circ \\BC = 100^\circ \end{array}\)
1بیشمار زاویه محاطی رو به روی یک کمان وجود دارد.
2 زوایای محاطی رو به روی یک کمان با هم برابرند.
\(\widehat A = \frac{{EF}}{2},\widehat B = \frac{{EF}}{2},\widehat C = \frac{{EF}}{2},\widehat D = \frac{{EF}}{2} \Rightarrow \widehat A = \widehat B = \widehat C = \widehat D\)
3 به چهارضلعی که چهار رأس آن روی محیط دایره باشد چهارضلعی محاطی گفته می شود و زاویه های روبرو در این چهارضلعی مکمل یکدیگرند.
\(\begin{array}{l}\widehat A + \widehat C = 180^\circ \\\widehat B + \widehat D = 180^\circ \end{array}\)
4 زاویه محاطی رو به روی قطر ۹۰ درجه است.
\(\widehat B = \frac{{AC}}{2} = \frac{{180^\circ }}{2} = 90^\circ \)
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی