درسنامه کامل فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی
تعداد بازدید : 7.59Mخلاصه نکات فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی - درسنامه شب امتحان فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی - جزوه شب امتحان فیزیک یازدهم تجربی نوبت اول فصل 3 مغناطیس و القای الکترومغناطیسی
میدان مغناطیسی
میدان مغناطیسی
آهن ربا
به موادی که براده های آهن را جذب می کند، آهن ربا می گویند. آهن، کبالت، نیکل و آلیاژ های آنها جذب آهن ربا می شوند از موادی که جذب آهن ربا می شوند می توان آهن ربا ساخت.
هر آهن ربایی دو قطب دارد.
ربایش در دو ناحیه از آهن ربا بیشتر از جاهای دیگر است، به این دو قطب می گویند.
1 قطبی را که تقریبا به سوی نیم کره شمالی زمین می ایستد، قطب شمال می نامند.
2 قطبی را که تقریبا به سوی نیم کره جنوبی زمین می ایستد، قطب جنوبی می نامند.
روش های آهن ربا کردن
1) بوسیله جریان الکتریسیته
یک تیغه فولادی را درون یک سیم پیچ قرار می دهیم و به جریان مستقیم وصل می کنیم، در مدت کوتاهی تیغه فولادی آهن ربا می شود.
2) مالش
یک قطب آهن ربا را در یک جهت معین از ابتدا تا انتهای میله ی مغناطیسی، می کشیم؛ به طور منظم این عمل را تکرار می کنیم. در این روش، انتهای میله که مالش به آن ختم می شود، همواره مخالف قطبی است که روی میله کشیده می شود.
3) بوسیله القا
یک آهن ربا را در نظر گرفته و در راستای آن یک تیغه فولادی قرار می دهیم، تیغه فولادی تحت اثر آهن ربایی که در بالای آن قرار دارد آهن ربا می شود. می گوییم در تیغه فولادی خاصیت مغناطیسی القا شده است.
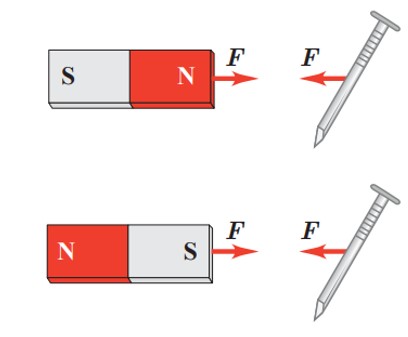
قطب های القای مغناطیسی همواره به گونه ای خواهد بود که قطعه های آهنی جذب آهن ربای اصلی می شوند.
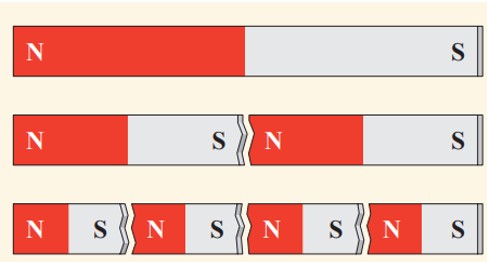
مجزا کردن قطب های مغناطیسی غیر ممکن است، چون هر قطعه جدا شده از آهن ربا، خود یک دو قطبی مجزا می شود.
میدان مغناطیسی
خاصیتی در اطراف هر آهن ربا که بر اجسام مغناطیسی موجود در این فضا، نیروی مغناطیسی وارد کند.
میدان مغناطیسی را با B نمایش می دهند که یک کمیت برداری است و به همین علت هم جهت و هم بزرگی دارد.
جهت میدان مغناطیسی B در هر نقطه از فضای پیرامون یک آهن ربا در جهتی است که وقتی عقربه مغناطیسی در آن نقطه قرار می گیرد، قطب N عقربه، جهت B ر معلوم می کند.
ویژگی های خط های میدان مغناطیسی
- بردار میدان مغناطیسی در هر نقطه، مماس و هم جهت با خط میدانی است که از آن نقطه می گذرد.
- خط های میدان یکدیگر را قطع نمی کنند.
- تراکم خط های میدان در هر ناحیه نشان دهنده بزرگی میدان مغناطیسی در آن ناحیه است.
- خط های میدان مغناطیسی، همواره منحنی های بسته ای هستند و به بیان دیگر تک قطبی وجود ندارد.
میدان مغناطیسی زمین
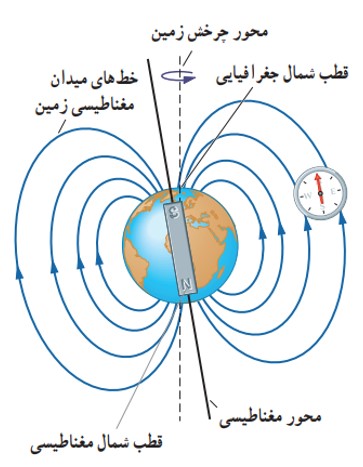
زمین یک آهن ربای بزرگ است که قطب S آن تقریبا در جهت شمال جغرافیایی زمین و قطب N آن در جنوب قرار دارد. قطب های مغناطیسی زمین دقیقا در محل قطب های جغرافیایی آن قرار ندارند.
شیب مغناطیسی
در بیشتر نقاط زمین عقربه مغناطیسی، به طور افقی قرار نمی گیرد و امتداد آن با سطح افقی زمین زاویه می سازد. به این زاویه، شیب مغناطیسی گفته می شود.
یا زاویه بی میدان مغناطیسی و راستای افقی را، شیب مغناطیسی می نامند.
میدان مغناطیسی یکنواخت
هر گاه در ناحیه ای از فضا جهت و اندازه میدان مغناطیسی یکسان باشد، به این میدان، میدان مغناطیسی یکنواخت می گویند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه تجربی- آزمون آنلاین تمامی دروس پایه تجربی
- گام به گام تمامی دروس پایه تجربی
- ویدئو های آموزشی تمامی دروس پایه تجربی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه تجربی
- فلش کارت های آماده دروس پایه تجربی
- گنجینه ای جامع از انشاء های آماده پایه تجربی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه تجربی
بار متحرک در میدان مغناطیسی
بار متحرک در میدان مغناطیسی
نیروی وارد بر ذره باردار متحرک در میدان مغناطیسی
هرگاه ذره بارداری در یک میدان مغناطیسی حرکت کند بر ذره باردار نیرو وارد می شود، بار الکتریکی از مسیر خود منحرف می شود به طوری که راستای نیرو بر راستای میدان و راستای حرکت عمود است.
جهت نیروی وارد بر بار متحرک
چهار انگشت باز شده دست راست را در جهت سرعت (V) ذره باردار مثبت طوری قرار می دهیم که، هنگامی که خم می شود، در جهت میدان مغناطیسی قرار گیرد، انگشت شست، سوی نیروی وارد بر ذره ی باردار مثبت را نشان می دهد.
جهت نیروی وارد بر ذره مثبت را با دست راست و نیروی وارد بر ذره منفی را با دست چپ نشان می دهیم.
تعریف کمی میدان مغناطیسی
بزرگی نیرویی که بر \(1c\) بار الکتریکی که با سرعت \(1\frac{m}{s}\) در راستای عمود بر خط های میدان قرار گرفته باشد، وارد می شود.
یکای میدان مغناطیسی تسلا نام دارد.
\(\begin{array}{l}B = \frac{F}{{qV\sin \alpha }}\\F = qVB\sin \alpha \end{array}\)
یکای کوچکتر میدان مغناطیسی گاوس نام دارد و با نماد G نمایش داده می شود.
\(\begin{array}{l}1T = {10^4}G\\1G = {10^{ - 4}}T\end{array}\)
اندازه میدان مغناطیسی زمین در نزدیکی سطح زمین در قطب ها بیشترین (\(0/65G\) ) و در استوا کمترین (\(0/25G\) ) است.
نمایش بردار عمود بر صفحه کاغذ
هر بار داخل صفحه کاغذ را به صورت شکل روبرو نمایش می دهند:
اگر برداری عمود بر صفحه کاغذ و به سمت داخل باشد به صورت \( \otimes \) نمایش می دهند.
اگر برداری عمود بر صفحه کاغذ و به سمت خارج باشد به صورت \( \odot \) نمایش می دهند.
مثال
بر پروتونی که با زاویه \(\theta = {30^0}\) نسبت به میدان مغناطیسی یکنواختی به اندازه \(B = 320G\) در حرکت است، نیرویی به اندازه \(F = 5/12 \times {10^{ - 14}}N\) وارد می شود. تندی پروتون چند کیلومتر بر ثانیه است؟
\(\begin{array}{l}q = 1/6 \times {10^{ - 19}}c\\\theta = {30^0}\\B = 320 \times {10^{ - 4}}T\\F = 5/12 \times {10^{ - 14}}N\\V = ?\\F = qVB\sin \theta \to V = \frac{F}{{qC\sin \theta }}\\V = \frac{{5/12 \times {{10}^{ - 14}}}}{{1/6 \times {{10}^{ - 19}} \times 320 \times {{10}^{ - 4}} \times 0/5}}\\V = 2 \times {10^7}\frac{m}{s} = 2 \times {10^4}\frac{{Km}}{s}\end{array}\)
جزوات جامع پایه تجربی
جزوه جامع فیزیک یازدهم تجربی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم تجربی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی
سیم حامل جریان در میدان مغناطیسی
سیم حامل جریان در میدان مغناطیسی
نیروی مغناطیسی وارد بر سیم حامل جریان به عوامل زیر بستگی دارد:
- با جریانی که از سیم می گذرد رابطه مستقیم دارد.
- با طول قسمتی از سیم که در میدان مغناطیسی قرار می گیرد رابطه مستقیم دارد.
- با بزرگی میدان مغناطیسی، رابطه مستقیم دارد.
- با سینوس زاویه ای که جریان با میدان مغناطیسی می سازد، رابطه مستقیم دارد.
فرمول نیروی مغناطیسی وارد بر سیم حامل جریان در میدان مغناطیسی
\(F = BIL\sin \alpha \)
در این فرمول
F نیروی مغناطیسی
B میدان مغناطیسی
I جریان الکتریکی
L طول سیم
\(\sin \alpha \) زاویه بین جریان با میدان
برای حفظ بهتر این فرمول می توان از اختصار بیل سینا استفاده کرد.
جهت نیروی مغناطیسی
نیروی مغناطیسی وارد بر سیم حامل جریان الکتریکی، بر راستای جریان و نیز بر میدان مغناطیسی عمود است.
جهت نیروی مغناطیسی را از قاعده دست راست بدست می آوریم.
قاعده دست راست
اگر چهار انگشت دست راست خود را در جهت جریان بگیرید به طوری که اگر انگشتان خود را خم کنید. در جهت میدان مغناطیسی قرار گیرد، در این صورت انگشت شست شما جهت نیروی وارد بر سیم حامل جریان را نشان خواهد داد.
بردار میدان همواره از کف دست خارج می شود.
مثال
یک سیم حامل جریان در میدان مغناطیسی به بزرگی \(0/04mT\) در راستایی که با جهت میدان زاویه 30 درجه می سازد، قرار دارد. اگر شدت جریانی که از سیم می گذرد \(5A\) باشد، نیروی مغناطیسی وارد بر یک متر از این سیم را محاسبه کنید.
\(\begin{array}{l}B = 0/04mT = 4 \times {10^{ - 5}}T\\\alpha = {30^0}\\I = 5A\\L = 1m\\F = ?\\\sin {30^0} = 0/5\\F = BIL\sin \alpha \\ \to F = 4 \times {10^{ - 5}} \times 5 \times 1 \times 0/5 \to F = 10 \times {10^{ - 5}} = {10^{ - 4}}N\end{array}\)
میدان مغناطیسی اطراف سیم دراز مستقیم
میدان مغناطیسی اطراف سیم دراز مستقیم
آثار مغناطیسی ناشی از جریان الکتریکی (آزمایش اورستد)
هرگاه یک عقربه مغناطیسی در اطراف سیمی که به باتری و کلید وصل شده است قرار گیرد، در لحظه وصل کلید، ملاحظه می شود که عقربه مغناطیسی منحرف می شود، بنابراین در اطراف سیم حامل جریان میدان مغناطیسی ایجاد می کند.
خطوط میدان مغناطیسی در اطراف یک سیم راست حامل جریان الکتریکی

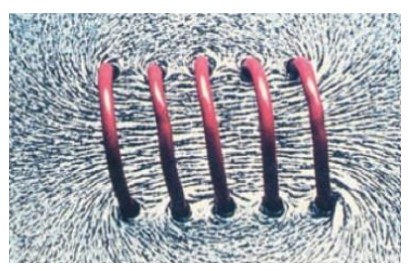
روی صفحه مقوایی که در وسط آن سیم راست حامل جریان قرار دارد؛ براده های آهن بپاشیم، این براده ها به صورت دایره هایی هم مرکز در خواهند آمد.
خطوط میدان مغناطیسی حاصل از یک سیم راست حامل جریان به صورت دایره های هم مرکزی در اطراف سیم راست هستند.
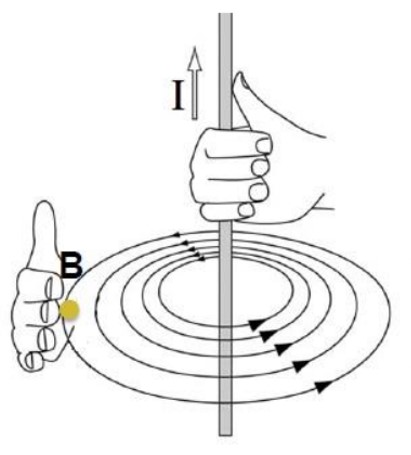
جهت میدان مغناطیسی در اطراف یک سیم راست حامل جریان الکتریکی
به این ترتیب است که اگر انگشت شست دست راست را در جهت جریان بگیریم، بسته شدن چهار انگشت، جهت میدان مغناطیسی را به ما می دهد.
نیروی بین سیم های موازی حامل جریان
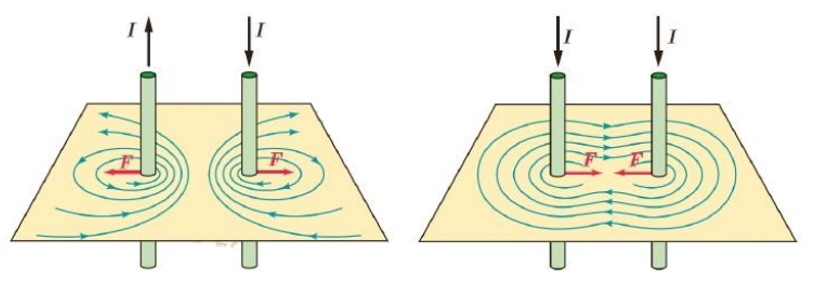
آزمایش نشان می دهد اگر از دو سیم راست و موازی جریان های الکتریکی عبور کند این دو سیم همدیگر را جذب یا دفع می کنند.
یعنی
اگر جریان ها هم جهت باشند همدیگر را جذب و اگر مخالف باشند همدیگر را دفع می کنند و علت آن ایجاد میدان یک سیم در محل سیم دیگر است.
میدان مغناطیسی ناشی از یک حلقه دایره ای سیملوله حامل جریان
پیچه مسطح، از چند دور سیم ناز به شکل حلقه به هم فشرده شده تشکیل شده است.

خطوط میدان مغناطیسی حاصل از یک پیچه ی مسطح:
یک مقوا را از وسط پیچه مسطح می گذرانیم و از آن جریان عبور می دهیم سپس روی مقوا براده می ریزیم شکل میدان در مقطع سیم ها به شکل دایره و در وسط حلقه به صورت یک خط راست خواهد بود.
خط های میدان مغناطیسی در ناحیه داخل پیچه به یکدیگر نزدیکترند. یعنی میدان در این ناحیه قوی تر است.
جهت میدان مغناطیسی دریچه
روش اول
اگر نوک انگشت شست دست راست را در جهت جریان قرار دهیم، بسته شدن انگشت دست راست، جهت میدان مغناطیسی را نشان می دهد.
روش دوم
اگر چهار انگشت دست راست را به صورت خمیده در جهت جریان در سیم پیچ قرار دهیم، آنگاه نوک انگشت شست، قطب N که همان جهت B هست.
سیملوله
اگر جریان الکتریکی از سیملوله عبور کند در فضای اطراف سیملوله خاصیت مغناطیسی ایجاد می شود.
اگر شعاع سیملوله نسبت به طولش کوچک باشد و حلقه های آن خیلی بهم نزدیک باشند. به این سیم لوله سیم لوله آرمانی گفته می شود.
میدان مغناطیسی داخل یک سیملوله آرمانی در نقطه های دور از لبه ها یکنواخت است.
بزرگی میدان مغناطیسی در محور سیملوله به عوامل زیر بستگی دارد:
- با شدت جریانی که از سیملوله می گذرد، نسبت مستقیم دارد.
- با تعداد حلقه های سیملوله نسبت مستقیم دارد.
- با طول سیملوله نسبت عکس دارد.
ضریب تناسب در SI برابر \({\mu _0}\) تراوایی مغناطیسی خلا است.
\(B = {\mu _0}\frac{N}{L}I\)
در این فرمول:
B بزرگی میدان
L طول سیملوله
N تعداد دور
I جریان الکتریکی
تعیین نوع قطب های سیملوله
روش اول
اگر نوک انگشت دست راست را در جهت جریان قرار دهیم، بسته شدن چهار انگشت دست راست، جهت میدان مغناطیسی را نشان می دهد.
روش دوم
اگر چهار انگشت دست راست خود را به صورت خمیده در جهت جریان در سیملوله قرار دهیم آنگاه انگشت شست قطب N که همان جهت B هست.
جهت میدان مغناطیسی در خارج از سیملوله از N به S و در داخل آن از S به N می باشد.
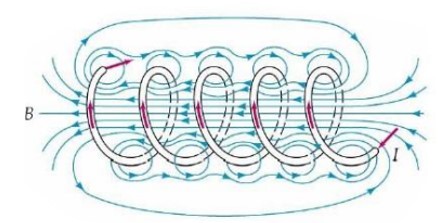
ویژگی های میدان مغناطیسی سیملوله
- خط های میدان داخل سیملوله، بسیار متراکم نر از خط های میدان در خارج آن است.
- میدان در داخل سیملوله دور از لبه ها یکنواخت است.
- جهت میدان در داخل و خارج سیملوله، خلاف هم هستند.
- شکل میدان سیملوله مانند میدان یک آهنربای میله ای است. که خطوط میدان منحنی های بسته ای را تشکیل می دهند.
مثال
جهت میدان مغناطیسی در سیملوله ی زیر را مشخص کنید.

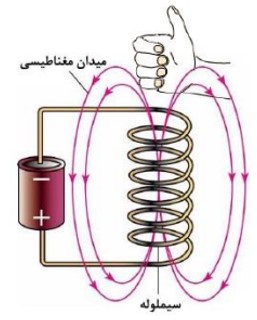
مثال
روی محور یک سیملوله ی حامل جریان به طول \(62/8cm\) ، میدان مغناطیسی به بزرگی \(0/02T\) ایجاد شده است. اگر تعداد حلقه های آن 2000 باشد، جریان گذرنده از آن چند آمپر است؟
\(\begin{array}{l}L = 62/8cm\\B = 0/02T\\N = 2000\\I = ?\\B = {\mu _0}\frac{N}{L}I \to I = \frac{{BL}}{{{\mu _0}N}}\\ \to I = \frac{{0/02 \times 62/8 \times {{10}^{ - 2}}}}{{4 \times 3/14 \times {{10}^{ - 7}} \times 2000}} \to I = 5A\end{array}\)
سیملوله با هسته آهنی – آهنربای الکتریکی
اگر داخل یک سیم لوله متصل به جریان یک هسته آهنی قرار دهیم، مجموعه را آهنربای الکتریکی می نامند.
توانایی آهنربای الکتریکی در ربایش قطعات آهنی به عوامل زیر بستگی دارد:
- جریانی که از سیملوله می گذرد.
- تعداد دور های واحد طول سیملوله
- جنس هسته آهنی سیملوله
قدرت آهنربای الکتریکی با افزایش شدت جریا و افزایش شمار دور های سیم لوله افزایش می یابد.
کاربرد های آهربای الکتریکی
هرگاه هسته ی درونی سیم پیچ از آهن خالص باشد، با برقراری جریا، هسته آهن ربا می شود و با قطع جریان، خاصیت خود را از دست می دهد. از این آهنربا ها در زنگ اخبار و جرثقیل های مغناطیسی و ... استفاده می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه تجربی- آزمون آنلاین تمامی دروس پایه تجربی
- گام به گام تمامی دروس پایه تجربی
- ویدئو های آموزشی تمامی دروس پایه تجربی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه تجربی
- فلش کارت های آماده دروس پایه تجربی
- گنجینه ای جامع از انشاء های آماده پایه تجربی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه تجربی
خاصیت مغناطیسی مواد
خاصیت مغناطیسی مواد
منشاء اصلی مغناطیسی
خاصیت مغناطیسی ناشی از حرکت الکترون به دور خودش است.
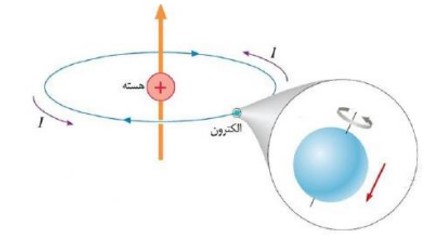
مواد دیامغناطیس:
اتم های این مواد به طور ذاتی فاقد خاصیت مغناطیسی اند. اتم های این مواد در حضور میدان مغناطیسی خارجی، می تواند سبب القای دو قطبی های مغناطیسی در خلاف سوی میدان خارجی، در مواد دیا مغناطیسی شود.
وقتی که در یک میدان مغناطیسی بسیار قوی قرار بگیرند میدان در داخل آنها اندکی ضعیف می شوند و از قطب های آهن ربا رانده می شونئ.
مانند: نقره، طلا، مس، نمک ها، ترکیب های آلی و تمام غیر فلز ها بجز اکسیژن
مواد مغناطیسی
موادی را که اتم های آن ها به طور ذاتی دارای دو قطبی مغناطیسی هستند.
نحوه سمت گیری دو قطبی های مغناطیسی کوچک در مواد مختلف، متفاوت است به همین دلیل مواد از لحاظ ویژگی های مغناطیسی نیز باهم تفاوت دارند.
مواد مغناطیسی
مواد پارا مغناطیس
مواد فرو مغناطیس
مواد فرو مغناطیس نرم
مواد فرو مغناطیس سخت
مواد پارا مغناطیس
دو قطبی های مغناطیسی این مواد، به طور کاتوره ای سمت گیری کرده اند و میدان مغناطیسی خالصی ایجاد نمی کنند. با قرار دادن مواد پارا مغناطیسی درون میدان مغناطیسی خارجی قوی دو قطبی های مغناطیسی آنها، در راستای خط های میدان مغناطیسی منظم می شوند. با دور کردن آهنربا از این مواد، دو قطبی های مغناطیسی آنها، دوباره به طور کاتوره ای سمت گیری می کنند.
مانند: اورانیم، پلاتین، آلومینیم، سدیم، اکسیژن، اکسید نیتروژن، فلز های قلیایی و قلیایی خاکی از جمله مواد پارامغناطیسی اند.
مواد پارا مغناطیس در حضور میدان های مغناطیسی قوی، خاصیت مغناطیسی ضعیف و موقت پیدا می کنند.
مواد فرومغناطیس
در برخی از مواد مغناطیسی، دو قطبی های مغناطیسی کوچک به طور خود به خود با دو قطبی های مجاور خود هم خط می شوند. این گونه مواد را فرو مغناطیس می نامند.
حوزه مغناطیسی
به ابعاد خیلی کوچکتر از میلی متر که تقریبا \({10^{19}}\) اتم وجود دارد و دو قطبی های مغناطیسی وابسته به آنها هم جهت اند. حوزه مغناطیسی می گویند.
مواد فرو مغناطیس در ابتدا آهنربا نمی شوند زیرا؛ سمت گیری و اندازه حوزه های مغناطیسی در ماده فرومغناطیس به گونه ای است که در کل اثر یکدیگر را خنثی می کنند لذا در مجموع آهنربا نیستند.
فرومغناطیس نرم
در برخی از مواد فرومغناطیس حجم حوزه ها در حضور میدان مغناطیسی به سهولت تغییر می کند و در نبود میدان مغناطیسی خاصیت آهنربایی خود را به آسانی از دست می دهند.
مانند: آهن، نیکل و کبالت در صورتی که خالص باشند.
کاربرد: ساخت آهنربای الکتریکی
جزوات جامع پایه تجربی
جزوه جامع فیزیک یازدهم تجربی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم تجربی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی
شار مغناطیسی
شار مغناطیسی
پدیده القای الکترو مغناطیسی
هرگاه جریان الکتریکی در یک رسانا القا گردد، به این پدیده (القای الکترو مغناطیسی) می گویند.
جریان القایی
حرکت آهنربا به سمت پیچه (دور و نزدیک شدن آهنربا از پیچه) باعث القای جریانی در پیچه می گردد، که به آن جریان القایی می گویند.
عوامل موثر در ایجاد جریان القایی
- با دور و نزدیک کردن آهنربا به پیچه، میدان در محل پیچه تغییر کرده و جریان القایی در مدار ایجاد می گردد. (تغییر در اندازه میدان مغناطیسی، در محل پیچه مدار بسته)
- اگر پیچه (انعطاف پذیر) در یک میدان مغناطیسی قرار دهید و از دو نقطه گرفته و بکشید، بطوری که شکل آن عوض شود، در اثر تغییر شکل، مساحت پیچه تغییر کرده و جریان در مدار به وجود می آید. (تغییر مساحت مدار بسته در میدان مغناطیسی)
- تغییر زاویه ین حلقه و راستای میدان مغناطیسی نیز می تواند عامل برقراری جریان الکتریکی القایی شود. (تغییر زاویه بین حلقه و راستای میدان مغناطیسی)
علت ایجاد جریان القایی در مدار
در اثر تغییر میدان مغناطیسی، یک میدان الکتریکی القایی در فضا ایجاد می شود و از آنجایی که مدار در این میدان الکتریکی قرار دارد بر الکترون های آزاد داخل آن نیرو وارد می شود و حرکت الکترون ها باعث ایجاد نیروی محرکه و جریان القایی، می شود.
تعریف شار مغناطیسی \(\Phi \)
معرف تعداد خطوط مغناطیسی که به طور عمود از یک سطح بسته می گذرند، شار مغناطیسی می گویند.
شار کمیتی نرده ای است.
بردار سطح
برای نمایش یک سطح، نیم خطی بر سطح پیچه عمود می کنیم. جهت این نیم خط همان جهت برداری سطح خواهد بود.
اگر یک سطح بچرخد، نیم خط عمود بر سطح N نیز با همان اندازه می چرخد.
فرمول شار مغناطیسی
\(\Phi = B \times A \times \cos \theta \)
در این فرمول
\(\Phi \) شار مغناطیسی و بر حسب وبر (wb)
B میدان مغناطیسی
A مساحت پیچه
\(\theta \) زاویه بین نیم خط عمود بر سطح پیچه و راستای میدان
1 بردار N را بر هر طرف سطح حلقه عمود کنیم، اهمیت ندارد. البته با تعویض جهت N، علامت \(\Phi \) تغییر خواهد کرد، ولی اندازه آن تغییر نمی کند.
2 در مسائل شار، اگر زاویه بین سطح قاب با سوی مثبت میدان مغناطیسی (\(\alpha \)) را داده باشند آنگاه:
3 زاویه بین نیم خط عمود بر سطح و سوی مثبت میدان مغناطیسی یعنی \(\alpha \) از رابطه ی زیر پیدا می شود.
\(\theta = \left| {90 - \alpha } \right|\)
تغییر شار مغناطیسی عبوری از یک حلقه
همواره دو جهت برای رسم نیم خط عمود بر یک سطح معین وجود دارد. علامت شار مغناطیسی عبوری از این سطح نیز به انتخاب این جهت بستگی دارد. در حل یک مسئله، همواره باید یک جهت را انتخاب کنیم و تا پایان آن را تغییر ندهیم، بنابراین ممکن است شار مثبت، منفی یا صفر شود.
\(\Delta \Phi = {\Phi _2} - {\Phi _1} \to \Delta \Phi = AB(\cos {\theta _2} - \cos {\theta _1})\)
یکای شار مغناطیسی
اگر قابی به مساحت \(1m{}^2\) عمود بر میدان مغناطیسی یکنواختی به بزرگی \(1T\) قرار گیرد، شار مغناطیسی گذرنده از آن برابر یک وبر (\(1wb\)) خواهد شد.
\(\Phi = BA\cos \theta \to 1wb = 1T \times 1{m^2} \times \cos 0\)
1 هرگاه سطح قاب عمود بر میدان مغناطیسی باشد، آنگاه \(\alpha = {90^0}\) بوده یعنی؛ شار عبوری از قاب ماکزیمم می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 90} \right| = {0^0} \to {\Phi _{\max }} = BA\\\cos {0^0} = 1\end{array}\)
2 هرگاه سطح قاب موازی میدان مغناطیسی باشد، آنگاه \(\alpha = 0\) بوده یعنی؛ شار عبوری از قاب صفر می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 0} \right| = {90^0} \to {\Phi _{\min }} = 0\\\cos {90^0} = 0\end{array}\)
تغییر شار مغناطیسی
هنگامی رخ می دهد که میدان مغناطیسی یا مساحت سطح و یا زاویه نیم خط عمود بر سطح رسانا با میدان، تغییر کند.
مثال
صفحه ای مربع شکل به ضلع \(20cm\) در یک میدان مغناطیسی یکنواخت به بزرگی \(3\mu T\) قرار دارد؛ به طوری که خط های میدان با سطح صفحه زاویه \({37^0}\) می سازند. شار مغناطیسی گذرنده از صفحه چند وبر است؟ (\(\cos 53 = 0/6\))
\(\begin{array}{l}a = 20cm = 0/2m \to A = {a^2} \to A = 4 \times {10^{ - 2}}{m^2}\\\alpha = {37^0} \to \theta = \left| {90 - \alpha } \right| \to \theta = \left| {90 - 37} \right| = {53^0}\\B = 3\mu T = 3 \times {10^{ - 6}}T\\\Phi = ?\\\Phi = BA\cos \theta \to \Phi = 3 \times {10^{ - 6}} \times 4 \times {10^{ - 2}} \times 0/6\\\Phi = 7/2 \times {10^{ - 8}}Wb\end{array}\)
قانون فارادی
قانون فارادی
هرگاه شار مغناطیسی ای که بسته ای می گذرد تغییر کند، نیروی محرکه ای در آن القا می شود که بزرگی نیروی محرکه القایی با آهنگ تغییر شار مغناطیسی متناسب است.
\(\varepsilon = - N\frac{{\Delta \Phi }}{{\Delta t}}\)
1 علامت منفی در رابطه به خاطر رعایت قانون لنز می باشد.
2 هنگامی که آهنگ تغییر شار مغناطیسی ثابت بماند، نیروی محرکه القایی متوسط \(\varepsilon \) برابر نیروی محرکه ای لحظه ای بوده و با نماد \(\varepsilon \) نمایش می دهیم.
مقدار شدت جریان القا شده از رابطه زیر بدست می آید:
\(I = \frac{\varepsilon }{R} \to I = - \frac{N}{R}\frac{{\Delta \Phi }}{{\Delta t}}\)
هر چه آهنگ تغییر شار مغناطیسی بیشتر باشد، نیروی محرکه القایی و در نتیجه جریان القایی تولید شده در مدار بیشتر خواهد بود.
هرگاه حلقه ای به هر وضعیتی که در یک میدان مغناطیسی قرار داشته باشد و شار عبوری از آن \(\Phi \) باشد، اگر حلقه حول خطی که در سطح حلقه است \({180^0}\) دوران نماید، شار عبوری از آن \( - \Phi \) می شود.
مثال
سیملوله ای با 500 دور در یک میدان مغناطیسی متغیر با زمان قرار گرفته است. مساحت مقطع سیملوله \(25c{m^2}\) و آهنگ تغییر میدان \(8 \times {10^{ - 3}}\frac{T}{s}\) است. بیشینه نیروی محرکه القایی متوسط در سیملوله را محاسبه کنید.
\(\begin{array}{l}N = 500\\A = 25 \times {10^{ - 4}}{m^2}\\\frac{{\Delta B}}{{\Delta t}} = 8 \times {10^{ - 3}}{m^2}\\\theta = 0\\\varepsilon = ?\\\varepsilon = - NA\frac{{\Delta B}}{{\Delta t}}\cos \theta \to \varepsilon = - 500 \times 25 \times {10^{ - 4}} \times 8 \times {10^{ - 3}} \times \cos 0 \to \varepsilon = - 0/01v = - {10^{ - 2}}v\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه تجربی- آزمون آنلاین تمامی دروس پایه تجربی
- گام به گام تمامی دروس پایه تجربی
- ویدئو های آموزشی تمامی دروس پایه تجربی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه تجربی
- فلش کارت های آماده دروس پایه تجربی
- گنجینه ای جامع از انشاء های آماده پایه تجربی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه تجربی
قانون لنز
قانون لنز
جریان حاصل از نیروی محرکه القایی در یک مدار در جهتی است که آثار مغناطیسی ناشی از آن، با عامل به وجود آورنده جریان القایی، یعنی تغییر شار مغناطیسی، مخالفت می کند.
علامت منفی در رابطه فارادی نشان دهنده همین مخالفت است.
به قوانین فارادی و لنز، قانون های القای الکترومغناطیسی می گویند.
1 جهت جریان القایی ایجاد شده در حلقه هم با افزایش شار و هم با کاهش شار عبوری از حلقه، مخالفت می کند.
2 هنگامی که شار گذرنده از حلقه در حال افزایش می باشد، میدان مغناطیسی القایی در خلاف جهت میدان اصلی به وجود می آید تا اثر تضعیف کننده آن با افزایش شار مخالفت کند.
3 هنگامی که شار گذرنده از حلقه در حال کم شدن باشد، میدان مغناطیسی القایی در جهت میدان مغناطیسی اصلی به وجود می آید تا اثر تقویت کننده آن با کاهش شار مخالف کند.
مثال
در شکل رو به رو با توجه به جهت جریان القایی در حلقه توضیح دهید، جریان در سیم راست در حال افزایش است یا کاهش؟
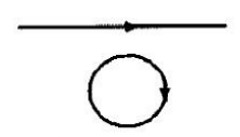
در حال کاهش، چون میدان مغناطیسی سیم راست هم جهت با میدان مغناطیسی حلقه است، طبق قانون لنز باید شار مغناطیسی در حال کاهش باشد یعنی جریان در حال کاهش است.
جزوات جامع پایه تجربی
جزوه جامع فیزیک یازدهم تجربی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم تجربی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم تجربی فصل 3 مغناطیس و القای الکترومغناطیسی
خود-القاوری
خود-القاوری
القاگر وسیله ای الکتریکی شبیه سیم پیچ با دو سر اتصال است که برای تولید میدان مغناطیسی و ذخیره انرژی مغناطیسی استفاده می شود.
القاگر می توانند میدان های مغناطیسی را در حجم های کوچک نگه دارند؛ همچنین می توان از آنه برای ذخیره کردن انرژی استفاده کرد.
خود-القاوری
در مدار شامل القاگری (پیچه یا سیملوله) باتری و رئوستا، آمپرسنج و القاگری است که به طور متوالی به یکدیگر بسته شده اند.
با تغییر مقاومت رئوستا، جریان در مدار تغییر می کند. تغییر جریان در مدار، سبب تغییر میدان مغناطیسی القاگر شده و در نتیجه شار مغناطیسی عبوری از آن نیز تغییر می کند. این فرایند سبب القای نیروی محرکه ای در القاگر می شود که بنابر قانون لنز با تغییر جریان عبوری از آن مخالفت می کند. این پدیده را اثر خود-القاوری نامیده می شود.
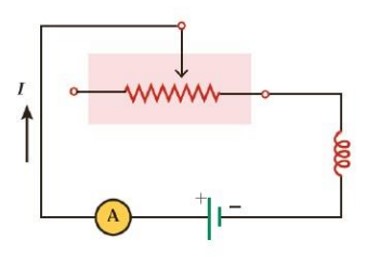
تغییر جریان در یک مدار باعث ایجاد نیروی محرکه ای القایی در همان مدار می شود، این پدیده را خود-القاوری می نامند.
نیروی محرکه ی خود القاوری \({\varepsilon _L}\)
اگر جریان گذرنده از سیملوله تغییر کند، به علت تغییر شار مغناطیسی گذرنده از آن، نیروی محرکه ای در خود مدار القا می شود که با عامل تغییر شار مغناطیسی که در اینجا تغییر جریان است مخالفت کند.
1 هرگاه جریان در مدار اصلی رو به افزایش باشد، جهت جریان خود- القاوری خلاف جهت جریان در مدار اصلی است.
2 هرگاه جریان در مدار اصلی رو به کاهش باشد، جهت جریان خود-القاوری هم جهت با جهت جریان در مدار اصلی است.
3 به هر قسمتی از یک مدار که خاصیت خود القاوری داشته باشد، القاگر می گویند.
4 پیچه و سیملوله در مداری با جریان متغیر القاگرند.
5 اثر خود-القاوری مخصوص جریان های متغیر است و در مدار های جریان پیوسته تنها به هنگام قطع و وصل کلید در مدار ایجاد می گردد.
ضریب القاوری (با نماد l نمایش می دهند.)
این پارامتر، ویژگی های فیزیکی القاگر را نشان می دهد و به عواملی همچون تعداد دور، طول و سطح مقطع القاگر و جنس هسته ای که داخل آن قرار می گیرد بستگی دارد.
یکای ضریب القاوری در SI، اهم در ثانیه (\(\Omega \times S\)) است که هانری نامیده و با H نشان داده می شود.
ضریب القاوری فقط به مشخصات ساختمانی سیم لوله بستگی دارد.
فرمول ضریب القاوری سیملوله
\(L = \frac{{AK{\mu _0}{N_2}}}{I}\)
در این فرمول
L ضریب القاوری
A مساحت هر حلقه ی سیملوله
K ضریب تراوایی نسبی هسته
\({\mu _0}\) ضریب تراوایی مغناطیسی خلاء
N تعداد دور های سیملوله
مثال
تعداد حلقه های سیملوله ای بدون هسته، به طول \(2/8cm\) و سطح \(10c{m^2}\) چه تعداد باشد تا ضریب القاوری آن \(1H\) شود؟
\(\begin{array}{l}K = 1\\I = 2/8 \times {10^{ - 2}}m\\A = 10 \times {10^{ - 4}}{m^2}\\N = ?\\L = 1H\\{\mu _0} = 4\pi \times {10^{ - 7}}\frac{{Tm}}{A}\\L = \frac{{AK{\mu _0}{N^2}}}{I} \to {N^2} = \frac{{IL}}{{AK{\mu _0}}}\\{N^2} = \frac{{2/8 \times 10 - 2 \times 1}}{{{{10}^{ - 3}} \times 1 \times 4 \times 3/14 \times {{10}^{ - 7}}}} \to {N^2} = 22 \times {10^6} \to N = 4/7 \times {10^3}\end{array}\)
القای متقابل
تغییر جریان در یک مدار باعث تغییر شار مغناطیسی در مدار دیگر و ایجاد نیروی محرکه القایی می شود.
با تغییر مقاومت رئوستا و تغییر جریان عبوری از پیچه 1 شار عبوری از پیچه 2 نیز تغییر می کند. این تغییر شار، سبب ایجاد نیروی محرکه القایی در پیچه 2 می شود. هم زمان تغییر جریان در پیچه 2، سبب ایجاد نیروی محرکه القایی در پیچه 1 می گردد.
انرژی ذخیره شده در القاگر
هنگامی که به دو سر القاگری اختلاف پتانسیل وصل کنیم، از طرف مولد به القاگر انرژی داده می شود. بخشی از این انرژی در مقاومت R تلف شده و بقیه آن در میدان مغناطیسی سیملوله ذخیره می شود. این انرژی از رابطه زیر بدست می آید:
\({U_L} = \frac{1}{2}L{I^2}\)
در این فرمول
\({U_L}\) انرژی ذخیره شده در القاگر
L ضریب القاوری
I شدت جریان در القاگر
جریان متناوب
جریان متناوب
تولید جریان متناوب
ساده ترین راه برای تغییر شار مغناطیسی و ایجاد جریان، تغییر زاویه است.
بنابراین معادله شار به صورت زیر می باشد:
\(\Phi = BA\cos \theta \)
که در آن \(\theta \) در حال تغییر است.
اجزای یک مولد (ژنراتور) جریان متناوب
حرکت یک میله گردان، باعث چرخش پیچه در فضای میدان مغناطیسی ناشی از یک آن ربا می شود. با گردش پیچه، زاویه آن با خطوط میدان و در نتیجه شار گذرنده از پیچه تغییر و نیروی محرکه و جریان الکتریکی در آن القا می شود.
دوره یا زمان تناوب T
زمانی که طول می کشد تا پیچه یک دور کامل بچرخد را دوره می نامند. یکای آن در SI ثانیه است.
\(T = \frac{t}{N}\)
بسامد یا فرکانس f
تعداد چرخش های کامل در مدت یک ثانیه را بسامد می نامند.
یکای بسامد (\({S^{ - 1}}\)) است که معادل هرتز HZ است.
\(f = \frac{1}{T}\)
مثال
قابی در دقیقه، 300 بار دور خود می چرخد. زمان تناوب و بسامد قاب را به دست آورید؟
\(\begin{array}{l}t = 1\min = 60s\\N = 300\\T = ?\\f = ?\\T = \frac{t}{N} \to T = \frac{{60}}{{300}} = 0/2s\\f = \frac{1}{T} \to f = \frac{1}{{0/2}} = 5HZ\end{array}\)
معادله نیروی محرکه متناوب
اگر هر دور کامل برابر \(2\pi \) و زمان یک دور چرخش کامل پیچه T باشد، \(\theta \) زاویه پیچه در مدت زمان t ثانیه چرخیدن از رابطه ی زیر پیدا می شود.
\(\varepsilon = {\varepsilon _m}\sin \frac{{2\pi }}{T}t\)
جریان متناوب
اگر جریان الکتریکی تولید شده در مدار، به طور سینوسی تغییر کند به چنین جریانی جریان متناوب می گویند.
\(I = {{\mathop{\rm I}\nolimits} _M}\sin \frac{{2\pi }}{T}t\)
انواع جریان
جریان مستقیم D.C
اگر مقدار و جهت شدت جریان متوسط در تمام بازه های زمانی ثابت بماند.
جریان متناوب A.C
اگر جهت جریان در زمان های مساوی به طور متناوب عوض می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه تجربی- آزمون آنلاین تمامی دروس پایه تجربی
- گام به گام تمامی دروس پایه تجربی
- ویدئو های آموزشی تمامی دروس پایه تجربی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه تجربی
- فلش کارت های آماده دروس پایه تجربی
- گنجینه ای جامع از انشاء های آماده پایه تجربی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه تجربی
مبدل ها
مبدل ها
مزایای مولد های AC نسبت به DC
1) در انتقال توان در فاصله های دور، از ولتاژ هرچه بالاتر و جریان هر چه متری استفاده کنیم، باعث کاهش اتلاف \(R{I^2}\) در خط های انتقال می شود.
2) در افزایش انرژی الکتریکی از نیروگاه به محل مصرف کننده توسط یک مبدل ولتاژ را افزایش و جریان را کاهش می دهند (طبق رابطه \(P = VI\) اگر توان تولیدی را ثابت فرض کنیم افزایش ولتاژ توسط یک مبدل با کاهش جریان همراه است) تا توان تلف شده در سیم ها انتقال (\(R{I^2}\)) به کمترین مقدار برسد.
نحوه کارکرد مبدل
مبدل شامل دو پیچه با روکش عایق که روی یک هسته آهنی پیچیده شده اند. اگر پیچه اولیه را به یک مولد جریان متناوب وصل کنیم، شار عبوری از آن نیز تغییر می کند، این شار متغییر از راه هسته از پیچه ثانویه عبور می کند و در اثر پدیده القای متقابل باعث القای نیروی محرکه الکتریکی در پیچه ثانویه می شود.
رابطه تعداد دور ها با ولتاژ در مبدل ها
میدان و شار مغناطیسی در داخل هسته آهنی بسیار بیشتر از خارج هسته است و می توان فرض کرد تمام شار تولید شده در پیچه اولیه از پیچه ثانویه عبور می کند.
\(\frac{{\Delta {\Phi _1}}}{{\Delta t}} = \frac{{\Delta {\Phi _2}}}{{\Delta t}} \to \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}} = \frac{{ - {N_2}\frac{{\Delta {\Phi _2}}}{{\Delta t}}}}{{ - {N_1}\frac{{\Delta {\Phi _1}}}{{\Delta t}}}} \to \varepsilon = V \to \frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}}\)
رابطه تعداد دور ها با شدت جریان در مبدل های ایده آل (آرمانی)
مبدلی را ایده آل گویند که هیچگونه اتلاف انرژی در آن وجود نداشته باشد. در نتیجه توان ورودی به مبدل آرمانی برابر توان خروجی از آن است.
\(P{}_{_1} = {P_2} \to {V_1}{I_1} = {V_2}I{}_2 \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{V_1}}}{{{V_2}}} \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{N_1}}}{{{N_2}}}\)
فرمول مبدل ها (ترانسفورماتور ها)
\(\frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}} = \frac{{{I_1}}}{{{I_2}}}\)
استفاده از مبدل برای کاهش اتلاف انرژی الکتریکی
در انتقال انرژی الکتریکی از نیروگاه به محل مصرف کنندخ توسط یک مبدل، ولتاژ را تا حد امکان افزایش و جریان را تا حد امکان کاهش می دهند تا توان تلف شده در سیم های انتقال برق (\(R{I^2}\)) به حداقل برسد.
توان تلف شده در خط انتقال
اگر توان تولیدی نیروگاه P ولتاژ بین خط های انتقال V باشد، شدت جریان در خط های فشار قوی \(I = \frac{P}{V}\) می شود. فرض می کنیم که مقاومت خط های انتقال برابر R باشد. در این صورت توان تلف شده \(P'\) در خط انتقال برابر می شود با:
\(P' = R\frac{{{P^2}}}{{{V^2}}}\)
رابطه ی مقایسه ای توان تلف شده در دو خط انتقال
خط انتقال توان، توان الکتریکی ثابت P را تحویل می گیرد. اگر انشعابی در مسیر نیروگاه تا مقصد وجود نداشته باشد، نسبت توان تلف شده در دو خط انتقال به صورت رابطه زیر است.
\(P' = R{I^2} \to P' = R\frac{{{P^2}}}{{{V^2}}} \to \frac{{{{P'}_1}}}{{{{P'}_2}}} = (\frac{{{R_1}}}{{{R_2}}}){(\frac{{{V_2}}}{{{V_1}}})^2}\)
مثال
توان تولیدی نیروگاهی \(2MW\) است. می خواهیم این انرژی را با کابل های مسی به طول \(20Km\) و سطح مقطع \(2c{m^2}\) انتقال دهیم. اگر ولتاژ خط های انتقال \(400kv\) باشد، توان تلف شده در خط های انتقال، چند ولت می شود؟
\(\begin{array}{l}P = 2 \times {10^6}W\\L = 20 \times {10^3}m\\A = 2 \times {10^{ - 4}}{m^2}\\V = 400 \times {10^3}kv\\P' = ?\\\rho = 1/8 \times {10^{ - 8}}\Omega m\\R = \rho \frac{L}{A} \to R = 1/8 \times {10^{ - 8}} \times \frac{{2 \times {{10}^4}}}{{2 \times {{10}^{ - 4}}}} \to R = 1/8\Omega \\P' = R\frac{{{P^2}}}{{{V^2}}} \to P' = 1/8 \times \frac{{{{(2 \times {{10}^6})}^2}}}{{{{(400 \times {{10}^3})}^2}}} \to P' = 45W\end{array}\)



1736019749.png)