درسنامه کامل حسابان دوازدهم فصل 2 مثلثات
تعداد بازدید : 7.59Mخلاصه نکات حسابان دوازدهم فصل 2 مثلثات - درسنامه شب امتحان حسابان دوازدهم فصل 2 مثلثات - جزوه شب امتحان حسابان دوازدهم نوبت اول فصل 2 مثلثات
تابع متناوب
تابع متناوب
به نمودار تابع زیر توجه کنید.
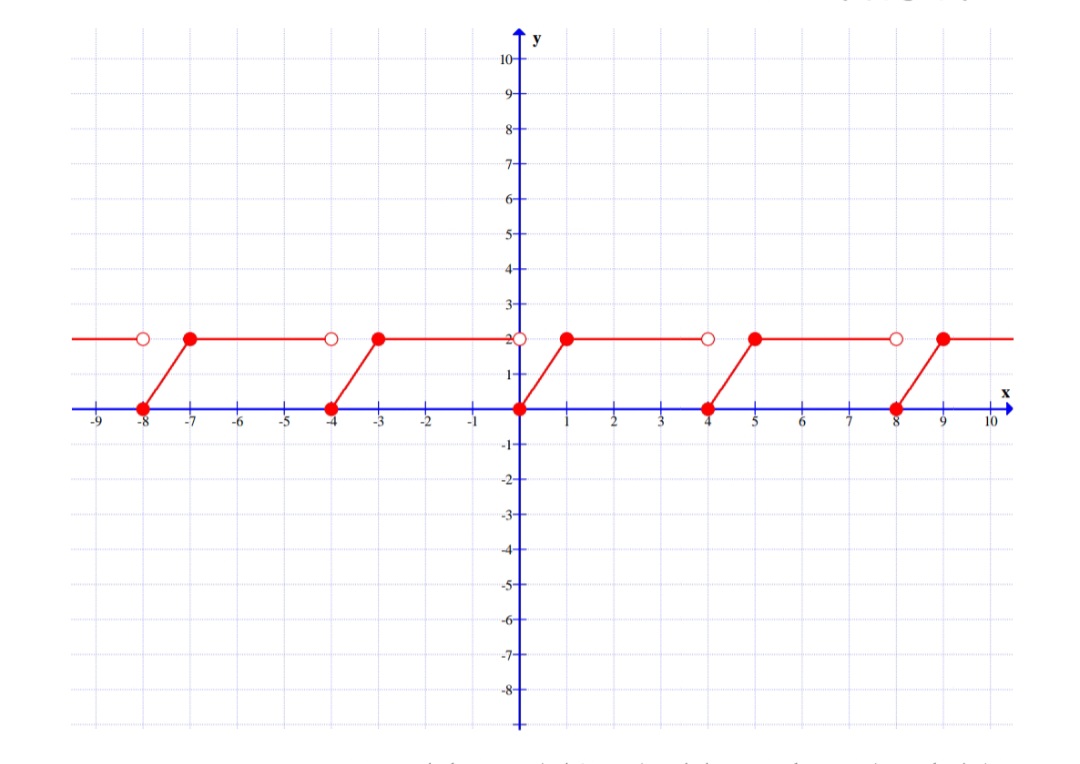
همانطور که مشاهده میکنید نمودار این تابع در فواصل معینی تکرار می شود.
می توان گفت که نمودار تابع در فواصل به طول ۴ و در فواصل به طول ۸ واحدی و .... تکرار می شود.
این چنین توابعی را توابع متناوب مینامند طول کوچکترین فاصله ای که نمودار تابع تکرار میشود را دوره ی تناوب می نامند و آن را با T نمایش میدهند در تابع فوق دوره ی تناوب برابر ۴ است.
نتیجه در واقع تابع متناوب تابعی است که در فواصل معینی نمودار آن تکرار می شود و دوره ی تناوب آن کوچکترین طول بازه ای است که در آن نمودار تابع تکرار می گردد.
اکنون تابع متناوب را به شکل زیر تعریف می کنیم.
اگر تابع (y = f(x دو شرط زیر را داشته باشد، آن را متناوب گویند.
الف) هرگاه عدد مثبتی مانند C وجود داشته باشد به طوری که وقتی x عضو دامنه باشد، آنگاه x + C نیز عضو دامنه است.
\(x \in {D_f}(x + c) \in {D_f}\)
ب \(f(x + c) = f(x)\)
در این صورت کمترین مقدار مثبت را با T نمایش میدهیم و آن را دوره ی تناوب )دوره ی تناوب اصلی) می نامیم.
مثال
نشان دهید که توابع زیر متناوب هستند.
\(f(x) = \sin x\) الف
\(f(x) = \cos x\) ب
الف واضح است که برای هر عدد صحیح k تساوی \(\sin (2k\pi + x) = \sin x\)برقرار است. لذا می توان \(f(2k\pi + x) = f(x)\) نوشت
پس طبق تعریف این تابع متناوب است و دوره ی تناوب آن به ازای ۱ k=برابر \(t = 2\pi \) است.
ب واضح است که برای هر عدد صحیح k تساوی \(cos(2k\pi + x) = \sin x\) برقرار است. لذا می توان \(f(2k\pi + x) = f(x)\) نوشت
پس طبق تعریف این تابع متناوب است و دوره ی تناوب آن به ازای ۱ k=برابر \(t = 2\pi \) است.

برای توابع \(f(x) = a\sin bx + c\) و \(f(x) = a\cos bx + c\) می توان گفت که :
الف مقدار ماگزیمم برابر \(\left| a \right| + c\)
ب دوره ی تناوب برابر \( - \left| a \right| + c\)
پ مقدار مینیمم برابر \(T = \frac{{2\pi }}{b}\)
مثال
مقدار ماگزیمم و مقدار مینیمم و دوره ی تناوب تابع به معادله ی \(f(x) = - 3\cos 2x + 5\) را تعیین کنید.
\(\left| a \right| + c = \left| { - 3} \right| + 5 = 8\) مقدار ماگزیمم
\( - \left| a \right| + c = - \left| 3 \right| + 5 = 2\) مقدار مینیمم
\(T = \frac{{2\pi }}{{\left| b \right|}} = \frac{{2\pi }}{{\left| 2 \right|}} = \pi \) دوره ی تناوب
مثال
معادله ی یک تابع سینوسی را بنویسید که مقدار ماگزیمم آن ۱ -و مقدار مینیمم آن ۷- و دوره ی تناوب آن \(4\pi \) باشد.
\( - \left| a \right| + c = - 7\) مقدار مینیمم
\(\left| a \right| + c = - 1\) مقدار ماگزیمم
\(f(x) = asinbx + c\)
با توجه به دو تساوی فوق می توان نتیجه گرفت که \(2c = - 8\) پس ۴- = c لذا :
\(\left| a \right| - 4 = - 1 \to \left| a \right| = 3 \to a = \pm 3\)
\(T = \frac{{2\pi }}{{\left| b \right|}} = 4\pi \to \left| b \right| = \frac{1}{2} \to b = \pm \frac{1}{2}\) دوره ی تناوب
پس می توان گفت که این تابع به یکی از شکل های زیر است.
\(f(x) = - 3sin\frac{1}{2}x - 4\) یا\(f(x) = 3sin\frac{1}{2}x - 4\)
مثال
معادله ی یک تابع سینوسی یا کسینوسی)برای نمودار زیر بنویسید.
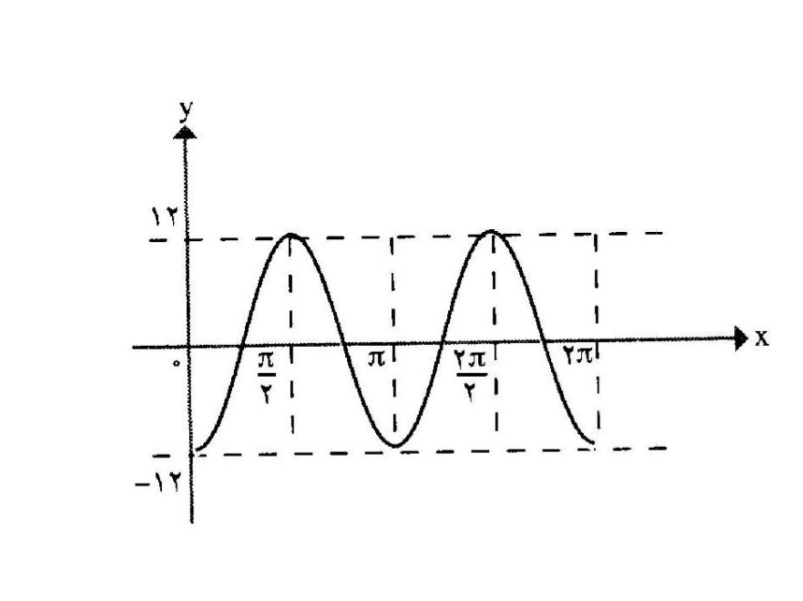
این تابع یک تابع کسینوسی است و معادله ی آن به صورت \(y = a\cos bx\) خواهد بود.
از طرفی با توجه شکل معلوم است که دوره ی تناوب تابع برابر \(T = \pi \) است. از
\(\frac{{2\pi }}{{\left| b \right|}} = \pi \to \left| b \right| = 2 \to b = \pm 2\)
برای تعیین مقدار a کافی است مختصات یک نقطه از نمودار تابع را در معادله ی فوق جایگزین کنیم در این جا می توان نقطه ی (,-12۰) را در نظر گرفت
\(y = a\cos bx - 12 = a\cos bx(0) \to - 12 = a \times 1 \to a = - 12\)
در نهایت معادله ی تابع را بدین شکل خواهیم داشت.
\(y = - 12\cos 2x\)
تهیه کننده : جابر عامری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
تابع تانژانت
تابع تانژانت
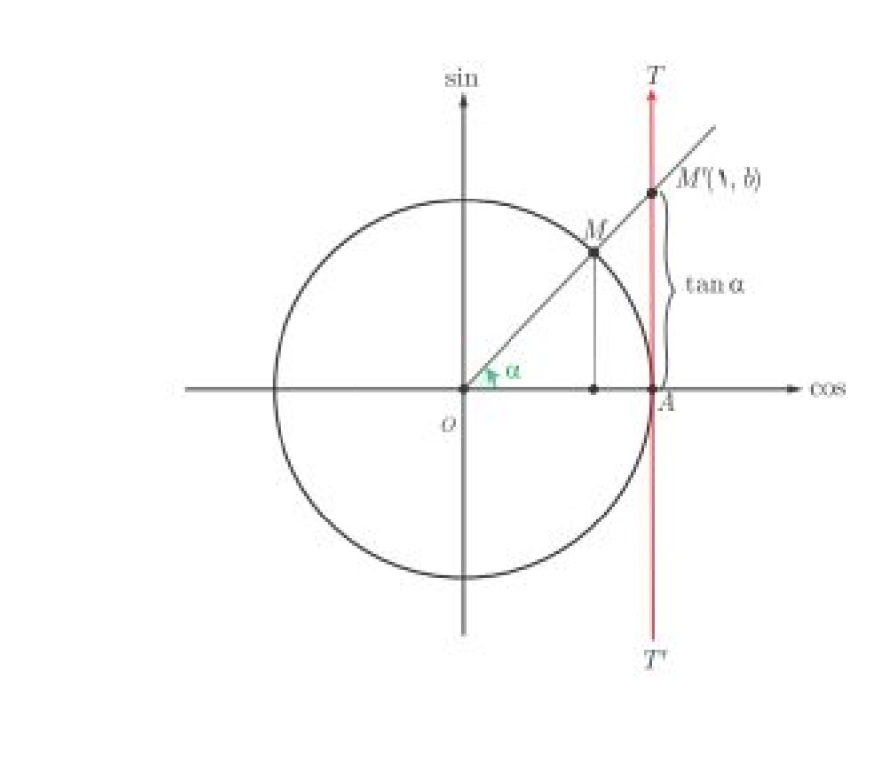
دایره ی مثلثاتی بالا را در نظر بگیرید. در این دایره خط\(T'AT\)در نقطه ی A بر محور کسینوس ها عمود است. اگر نقطه ی A مبدأ این محور و جهت آن از پایین به بالا فرض شود طبق تعریف تانژانت می دانیم که \(tan\left( \alpha \right){\rm{ }} = {\rm{ }}AM'\) و با توجه به مختصات نقطه ی \(M'\) میتوان نوشت \(tan\left( \alpha \right){\rm{ }} = {\rm{ b}}\)
با این دید میتوان گفت که با تغییر زاویه ی\(\alpha \)مقدار \(tan\left( \alpha \right)\) نیز تغییر میکند لذا می توان گفت که \(f(x) = tan\left( \alpha \right)\) تابعی از زاویه ی \(\alpha \)است. این تابع را تابع تانژانت مینامند تابع تانژانت دارای ویژگی های زیر است.
الف : اگر زاویه ی \(\alpha \)در ربع اول یا سوم باشد، مقدار تابع مثبت است.
ب : اگر زاویه ی\(\alpha \) در ربع دوم یا چهارم باشد مقدار تابع منفی است.
ج : اگر زاویه ی\(\alpha \) برابر صفر یا رادیان باشد مقدار تابع صفر است.
د : تابع در نقاط\(\frac{\pi }{2}\) و \(\frac{{3\pi }}{2}\) تعریف نمی شود. به طور کلی د دامنه و برد تابع تانژانت به شکل زیر است.
\(\begin{array}{l}{D_f} = \left\{ {x \in \left. R \right|} \right.x \ne k\pi + \frac{\pi }{2},k \in \left. z \right\}\\\\{R_f} = R\end{array}\)
و : چون \(\tan (\pi + x) = \tan (x)\) پس این تابع متناوب است و دوره ی تناوب آن \(T = \pi \) می باشد.
به طور کلی دوره ی تناوب تابع \(f(x) = a\tan (bx) + c\) برابر \(T = \frac{\pi }{{\left| b \right|}}\) است.
تغییرات تانژانت
با افزایش مقدار \(\alpha \)در ربع اول مقدار تابع افزایش می یابد. بانزدیک شدن مقدار\(\alpha \) به\(\frac{\pi }{2}\) مقدار تابع ز زیاد و زیادتر می شود.

تانژانت مجموع و تفاضل دو زاویه
در این قسمت در پی آن هستیم رابطه هایی برای محاسبه ی تانژانت مجموع و تفاضل دو زاویه بیان کنیم به کمک روابطی که در سال گذشته برای سینوس و کسینوس مجموع و تفاضل دو زاویه داشتیم می توان نوشت:
\(\begin{array}{l}\tan (\alpha + \beta ) = \frac{{sin(\alpha + \beta )}}{{cos(\alpha + \beta )}}\\\\\frac{{sin\alpha .cos\alpha + cos\alpha .\sin \beta }}{{sin\alpha .cos\alpha - cos\alpha .\sin \beta }} = \frac{{\frac{{sin\alpha .cos\alpha + cos\alpha .\sin \beta }}{{cos\alpha .cos\beta }}}}{{\frac{{cos\alpha .cos\beta - \sin \alpha .\sin \beta }}{{cos\alpha .cos\beta }}}}\\\\\frac{{\frac{{sin\alpha .cos\beta }}{{cos\alpha .cos\beta }} + \frac{{cos\alpha .\sin \beta }}{{cos\alpha .cos\beta }}}}{{\frac{{cos\alpha .cos\beta }}{{cos\alpha .cos\beta }} - \frac{{\sin \alpha .\sin \beta }}{{cos\alpha .cos\beta }}}} = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha .\tan \beta }}\\\\\tan (\alpha - \beta ) = \tan (\alpha + ( - \beta )) = \frac{{\tan \alpha + \tan ( - \beta )}}{{1 - \tan \alpha .\tan ( - \beta )}} = \frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha .\tan \beta }}\end{array}\)
لذا خواهیم داشت:
\(\tan (\alpha - \beta ) = \frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha .\tan \beta }}\) (ب
\(\tan (\alpha + \beta ) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha .\tan \beta }}\) (الف
مثال
تانژانت زاویه ی ۷۵ درجه را حساب کنید.
\(\tan {75^o} = tan(30 + 45) = \frac{{\tan 30 + \tan 45}}{{1 - \tan 30 \times \tan 45}} = \frac{{\frac{{\sqrt 3 }}{3} + 1}}{{1 - (\frac{{\sqrt 3 }}{3} \times 1)}} = \frac{{3 + \frac{{\sqrt 3 }}{3}}}{{1 - (\frac{{\sqrt 3 }}{3} \times 1)}} = \frac{{3 + \sqrt 3 }}{{3 - \sqrt 3 }}\)
تهیه کننده : جابر عامری
جزوات جامع پایه دوازدهم
جزوه جامع حسابان دوازدهم فصل 1 تابع
جزوه جامع حسابان دوازدهم فصل 2 مثلثات
جزوه جامع حسابان دوازدهم فصل 3 حدهای نامتناهی_حد در بی نهایت
جزوه جامع حسابان دوازدهم فصل 4 مشتق
جزوه جامع حسابان دوازدهم فصل 5 کاربردهای مشتق
معادلات مثلثاتی
معادلات مثلثاتی
هر معادله که شامل نسبتهای مثلثاتی باشد را معادله ی مثلثاتی مینامند در هر معادله ی مثلثاتی، اطلاعاتی از نسبت های مثلثاتی یک زاویه ی مجهول را داریم و منظور از حل معادله ی مثلثاتی یافتن زاویه یا زاویه هایی است که به ازاء آنها تساوی برقرار باشد
مثال
به یک معادله ی جبری و معادله ی مثلثاتی توجه کنید.
الف معادله ی جبری
\(2x - 1 = 0\)
\(2x - 1 = 0 \to x = \frac{1}{2}\)
ب معادله ی مثلثاتی
\(2\sin x - 1 = 0\)
\(2\sin x - 1 = 0 \to sinx = \frac{1}{2}\)
بیشمار زاویه وجود دارند که سینوس انها برابر\(\frac{1}{2}\)می شود. می برای تعیین زاویه های دیگر می نویسیم. ولی کوچکترین زاویه ی مثبت از بین آنها\(\frac{\pi }{2}\) است.
\(\left\{ \begin{array}{l}x = 2k\pi + \frac{\pi }{6}\\\\x = 2k\pi + \pi - \frac{\pi }{6} = 2k\pi + \frac{{5\pi }}{6}\end{array} \right.\)
این جواب را جواب عمومی معادله می نامند که در آن kیک عدد صحیح است. در واقع با اختیار مقداری برای یک جواب برای معادله ی مثلثاتی به دست می آید.
برای حل هر معادله ی مثلثاتی باید ابتدا با انجام ۱۴ از ۲۴ به جواب عمومی آن را تعیین کرد.
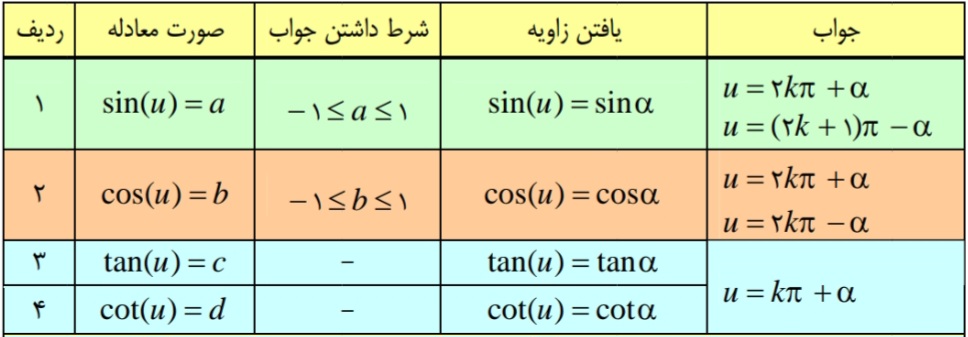
تذکر با توجه به این جدول
1)اگر مقادیر a و c منفی باشد در فرمول جواب قرینه ی زاویه ی \(\alpha \) را قرار دهید.
2)اگر مقادیر b و d منفی باشد در فرمول جواب قرینه ی زاویه ی \(\alpha \) را قرار دهید.
3)کوچکترین زاویه ی منفی است که تساوی به ازای آن برقرار میباشد و انرا زاویه اصلی می نامند.
برای تعیین زاویه ی اصلی در صورت وجود میتوانید از جدول مقادیر نسبتهای مثلثاتی استفاده کنید و در غیر این صورت می توانید به ذکر\(\alpha \)اکتفا کنید.
مثال
معادله ی زیر را حل کنید.
\(2\sin x - \sqrt 2 = 0\)
\(2\sin x - \sqrt 2 = 0 \to \sin x = \frac{{\sqrt 2 }}{2}\left\{ \begin{array}{l}x = 2k\pi + \frac{\pi }{4}\\\\x = 2(k + 1)\pi - \frac{\pi }{4}\end{array} \right.\)
مثال
معادله ی زیر را حل کنید.
\(2\cos x - 1 = 0\)
\(\cos x = \frac{1}{2} \to \left\{ \begin{array}{l}x = 2k\pi + \frac{\pi }{3}\\\\x = 2k\pi - \frac{\pi }{3}\end{array} \right.\)
مثال
معادله ی زیر را حل کنید.
\(\sin 3x - 1 = 0\)
\(\sin 3x = 1\left\{ \begin{array}{l}3x = 2k\pi + \frac{\pi }{2} \to x = \frac{{2k\pi }}{3} + \frac{\pi }{6}\\\\3x = (2k + 1)\pi - \frac{\pi }{2} \to x = \frac{{(2k + 1)\pi }}{3} - \frac{\pi }{6}\end{array} \right.\)
مثال
معادله ی \(\tan 4x.\tan 3x = 1\) را حل کنید.
\(\begin{array}{*{20}{l}}\begin{array}{l}\tan 4x.\tan 3x = 1 \to \tan 4x = \frac{1}{{\tan 3x}}\\\\ \to \tan 4x = \cot 3x \to \tan \underbrace u_{} = \tan (\underbrace {\frac{\pi }{2} - 3x}_\alpha )\end{array}\\{}\\\begin{array}{l} \to 4x = 4\pi + \frac{\pi }{2} - 3x \to 7x = k\pi + \frac{\pi }{2}\\\\ \to x = \frac{{k\pi }}{7} + \frac{\pi }{{14}}\end{array}\end{array}\)
مثال
معادله ی زیر را حل کنید.
\(\tan x.\tan 2x = 1\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\tan x.\tan 2x = 1 \to \tan 2x = \frac{1}{{\tan x}}\\\\ \to \tan 2x = \cot x \to \tan 2x = \tan (\frac{\pi }{2} - x)\end{array}\\{}\\\begin{array}{l} \to 2x = k\pi + (\frac{\pi }{2} - x)\\\\ \to 3x = k\pi + \frac{\pi }{2} \to x = \frac{{k\pi }}{3} + \frac{\pi }{6}\end{array}\end{array}\)
توجه داشته باشید که این معادله به ازای برخی از مقادیر بدست آمده برقرار نیست. مثلاً به ازای ۱ = k به دست می آید. \(x = \frac{\pi }{3} + \frac{\pi }{6} = \frac{\pi }{2}\) که جواب معادله نیست.
تهیه کننده : جابر عامری
حالت های خاص معادلات مثلثاتی
حالت های خاص معادلات مثلثاتی
علاوه بر جدول کلی فوق در حل معادلات مثلثاتی میتوان از حالتهای خاص زیر نیز استفاده نمود.
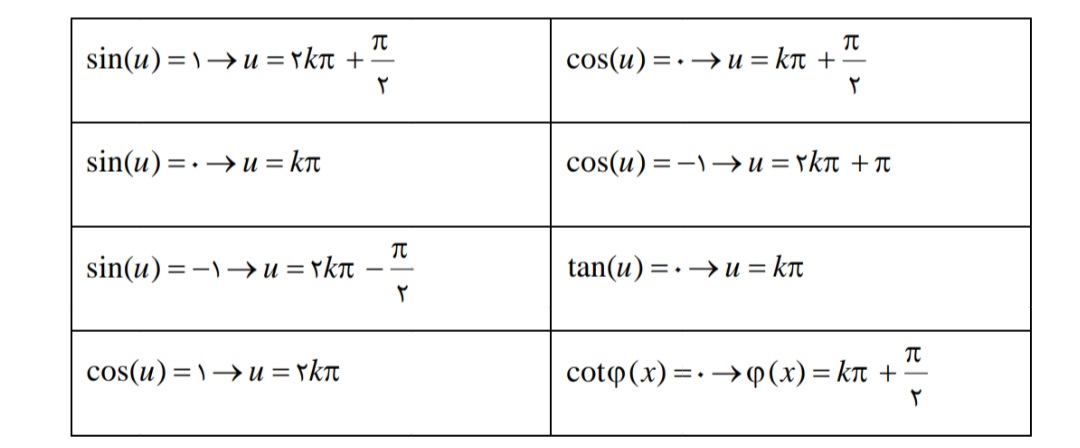
مثال
معادله ی زیر را حل کنید.
\(\sin 2x - 1 = 0\)
\(\sin 2x = 1\to2x = 2k\pi + \frac{\pi }{2} \to x = k\pi + \frac{\pi }{4}\)
مثال
معادله ی زیر را حل کنید.
\({\sin ^2}x + \sin x = 0\)
\(\sin x(\sin x + 1) = 0 \to \left\{ \begin{array}{l}\sin x = 0 \to x = k\pi \\\\\sin x = - 1 \to x = 2k\pi - \frac{\pi }{2}\end{array} \right.\)
مثال
معادله ی زیر را حل کنید.
\({\sin ^2}x - 3\sin x + 2 = 0\)
\((\sin x - 1)(\sin x + 2) = 0 \to \left\{ \begin{array}{l}\sin x = 1\to x = 2k\pi + \frac{\pi }{2}\\\\\sin x = - 2\end{array} \right.\)
مثال
الف تساوی مقابل را ثابت کنید.
\(\sin x + \cos x = \sqrt 2 \sin (x + \frac{\pi }{4})\)
\(\begin{array}{l}\sin x + \cos x = 1\\\\\sqrt 2 \sin (x + \frac{\pi }{4}) = 1 \to x + \frac{\pi }{4} = 2k\pi + \frac{\pi }{2} \to x = 2k\pi + \frac{\pi }{4}\end{array}\)
یادآوری : دو تساوی مهم و مفید را به خاطر داشته باشید.
\(\sin x + \cos x = \sqrt 2 \sin (x + \frac{\pi }{4})\) الف
\(\sin x - \cos x = \sqrt 2 \sin (x - \frac{\pi }{4})\) ب

به کمک جواب عمومی میتوانید مجموعه ی جوابهای معادله را در یک محدوده ی مشخص را نیز تعیین کرد. برای این کار مقدار مختلف برای kاختیار کنید.
مثال
معادله ی زیر را حل کنید و مجموعه ی جواب های آن را در فاصله ی \(\left[ {0,2\pi } \right]\) را تعیین کنید.
\(2\sin 2x - 1 = 0\)
\(\begin{array}{l}2\sin 2x - 1 = 0 \to \sin 2x = \frac{1}{2}\\\\\left\{ \begin{array}{l}2x = 2k\pi + \frac{\pi }{6} \to x = k\pi + \frac{\pi }{{12}}(1)\\\\2x = (2k + 1)\pi - \frac{\pi }{6} \to x = 2k\pi + \frac{{5\pi }}{6} \to x = k\pi + \frac{{5\pi }}{{12}}(2)\end{array} \right.\end{array}\)
اکنون برای هر یک از جوابهای عمومی بدست آمده جدولی مشابه جدول زیر تنظیم می کنیم و با انتخاب مقادیر مختلف برایk ، جوابهای مورد نظر در محدوده داده شده را تعیین می کنیم.

لذا مجموعه ی جواب در فاصله ی داده شده برابر \(\left\{ {\frac{\pi }{{12}}} \right.,\frac{{5\pi }}{{12}},\frac{{13\pi }}{{12}},\left. {\frac{{17\pi }}{{12}}} \right\}\)
مثال
معادله ی زیر را حل کنید و مجموعه ی جواب های آن را در فاصله ی \(\left[ { - 2\pi ,2\pi } \right]\) را تعیین کنید.
\(co{s^2}x - {\mathop{\rm sinx}\nolimits} = \frac{1}{4}\)
\(\begin{array}{l}1 - {\sin ^2}x - {\mathop{\rm sinx}\nolimits} = \frac{1}{4} \to {\sin ^2}x + {\mathop{\rm sinx}\nolimits} = \frac{3}{4} \to 4{\sin ^2}x + 4{\mathop{\rm sinx}\nolimits} - 3 = 0\\\\\left\{ \begin{array}{l}\sin x = \frac{{ - 4 + 8}}{8} = \frac{1}{2}\\\\\sin x = \frac{{ - 4 - 8}}{8} = \frac{{ - 3}}{2}\end{array} \right.\end{array}\)
اکنون معادله ی (۱) را به شکل زیر ادامه می دهیم.
\(\left\{ \begin{array}{l}x = 2k\pi + \frac{\pi }{6}\\\\x = (2k + 1)\pi - \frac{\pi }{6}\end{array} \right.\)
لذا مجموعه ی جواب در فاصله ی داده شده برابر \(\left\{ {\frac{\pi }{6}} \right.,\frac{{5\pi }}{6},\frac{{ - 7\pi }}{6},\left. {\frac{{ - 11\pi }}{6}} \right\}\)
حل چند تمرین کاربردی برای معادلات مثلثاتی
آیا میتوان مثلثی رسم کرد که طول دو ضلع آن ۲ و ۶ سانتی متر باشد و مساحت آن ۳ سانتی متر مربع شود. مسئله چند جواب دارد؟
فرض کنیم که چنین مثلثی وجود داشته باشد. لذا
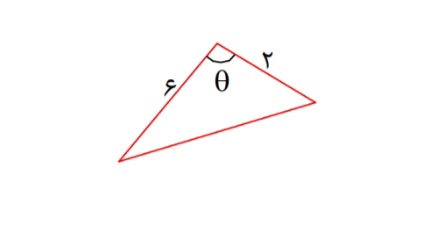
\(\begin{array}{l}s = 3\to\frac{1}{2}(2)(6)sin\theta = 3 \to sin\theta = \frac{1}{2}\\\\\left\{ \begin{array}{l}\theta = 2k\pi + \frac{\pi }{6}\\\\\theta = (2k + 1)\pi - \frac{\pi }{6}\end{array} \right.\end{array}\)
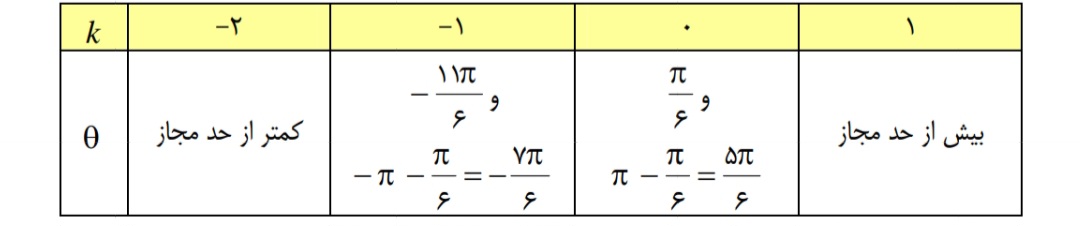
حال مقدار 0 مجاز را تعیین می کنیم.

لذا دو مثلث با چنین شرایطی ) زاویه های داخلی هر مثلث مثبت و کمتر از ۱۸۰ درجه ) وجود دارد.
در مثلثی طول اضلاع آن ۱ و ۳ و \(\sqrt 7 \) است. زاویه ی روبروی ضلع به طول \(\sqrt 7 \) چقدر است؟

\(\begin{array}{l}0 < \theta < \pi \\\\({\sqrt {7)} ^2} = {\left( 1 \right)^2} + {\left( 3 \right)^2} - 2(1)(3)\cos \theta \to \cos \theta = \frac{1}{2}\\\\\left\{ \begin{array}{l}\theta = 2k\pi + \frac{\pi }{3}\\\\\theta = (2k + 1)\pi - \frac{\pi }{3}\end{array} \right.\end{array}\)
حال مقدار مجاز را تعیین می کنیم.

لذا یک مثلث با چنین شرایطی وجود دارد و در آن\(\theta = \frac{\pi }{3}\) می باشد.
یک بازیکن هندبال توپ را با سرعت 16متر بر ثانیه برای هم تیمی خود که در 12/8متری او قرار دارد پرتاب می کند. اگر رابطه ی بین سرعت توپ (vبر حسب متر بر ثانیه (مسافت طی شده افقی (dبرحسب متر) و زاویه ی پرتاب \(\theta \) به صورت زیر باشد. آنگاه زاویه ی پرتاب توپ چقدر بوده است؟
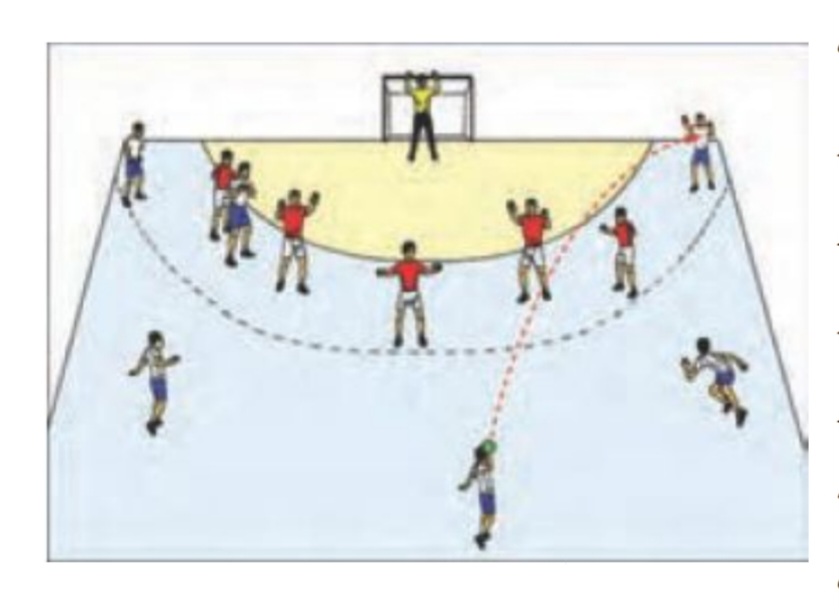
\(d = \frac{{{v^2}\sin 2\theta }}{{10}}\)
\(\begin{array}{l}0 < \theta < \pi \\\\12/8 = \frac{{{{(16)}^2}\sin 2\theta }}{{10}} \to \sin 2\theta = \frac{{12/8 \times 10}}{{256}} = \frac{1}{2} \to \left\{ \begin{array}{l}2\theta = 2k\pi + \frac{\pi }{6}\\\\2\theta = (2k + 1)\pi - \frac{\pi }{3}\end{array} \right.\\\\ \to \left\{ \begin{array}{l}\theta = k\pi + \frac{\pi }{{12}}\\\\\theta = (2k + 1)\frac{\pi }{2} - \frac{\pi }{{12}}\end{array} \right.\end{array}\)

π با توجه به شکل جواب قابل قبول \(\theta = \frac{\pi }{{12}}\) می باشد. ۱۲
شکل زیر زاویه ی دید دوربین \((\beta )\) با فاصله ی افقی آن با تابلو نقاشی را نشان می دهد.
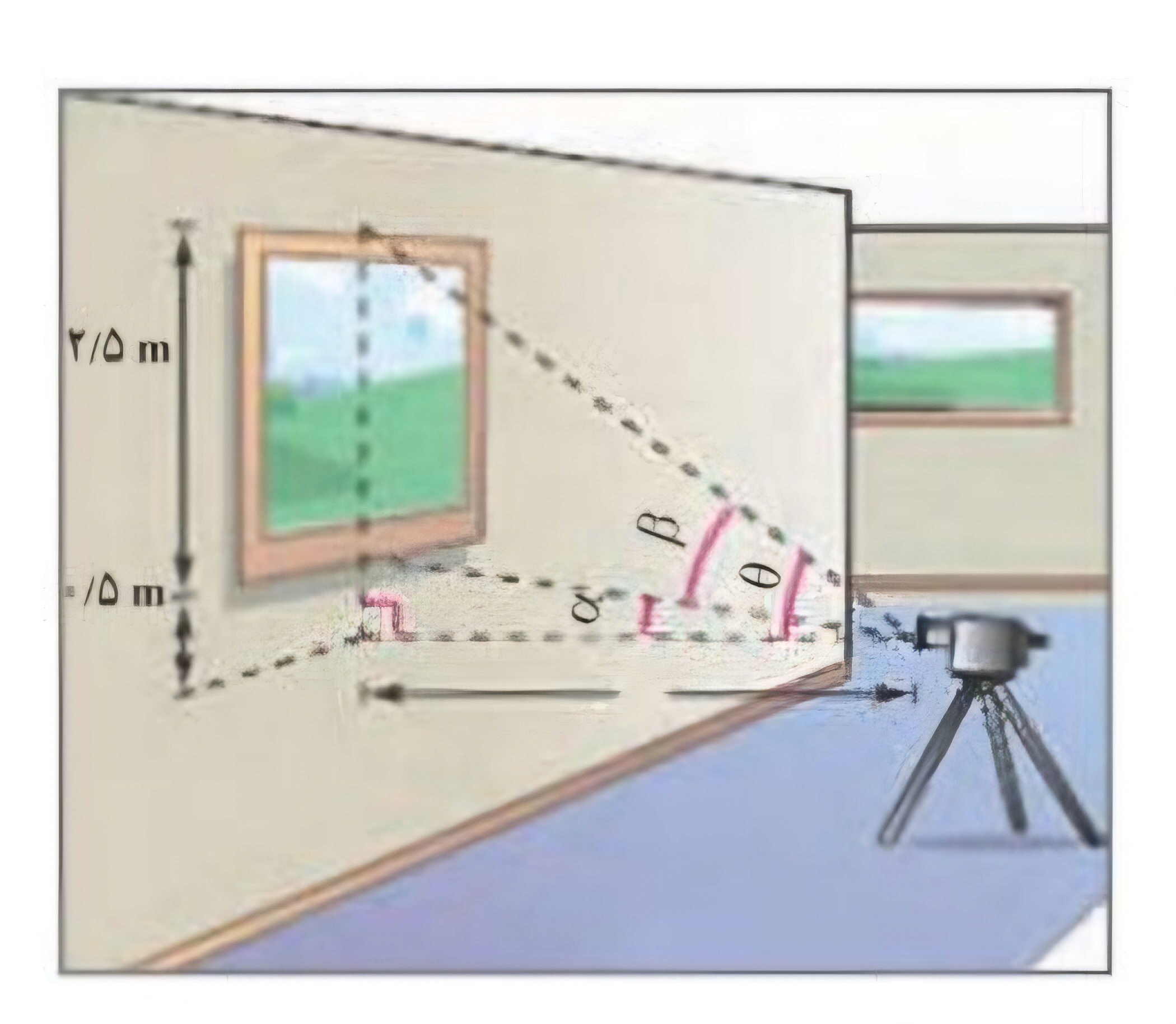
اولاً : نشان دهید که رابطه ی بین زاویه ی دید دوربین \((\beta )\) با فاصله ی افقی آن با تابلو نقاشی به صورت زیر است.
\(\tan \beta = \frac{{5x}}{{2{x^2} + 3}}\)
ثانیاً : زاویه ی دید را در حالتی که فاصله ی افقی برابر یک متر است، به دست آورید.
\(\tan \alpha = \frac{{0/5}}{x}\)
همچنین برای مثلث بزرگ که یک زاویه ی آن \(\theta \) است. داریم :
\(\tan \theta = \frac{3}{x}\)
اکنون با استفاده از رابطه ی تفاضل زوایا برای تانژانت به دست می آید.
\(\begin{array}{l}\tan \beta = \tan (\theta - \alpha ) = \frac{{tan\theta - \tan \alpha }}{{1 + tan\theta - \tan \alpha }} = \frac{{\frac{3}{x} - \frac{{0/5}}{x}}}{{1 + \frac{3}{x} \times \frac{{0/5}}{x}}} = \frac{{\frac{{2/5}}{x}}}{{1 + \frac{{1/5}}{{{x^2}}}}} = \frac{{\frac{{2/5}}{x}}}{{\frac{{{x^2} + 1/5}}{{{x^2}}}}}\\\\\frac{{\frac{5}{{2x}}}}{{\frac{{2{x^2} + 3}}{{2{x^2}}}}} = \frac{{5x}}{{2{x^2} + 3}}\end{array}\)
وقتی فاصله ی افقی برابر یک متر است. آنگاه :
\(\tan \beta = \frac{{5(1)}}{{2{{(1)}^2} + 3}} = 1\to\beta = k\pi + \frac{\pi }{4}\)
لیکن با توجه به شکل تنها جواب منطقی در حالت 0=k است که در آن \(\beta = \frac{\pi }{4}\) را به دست می دهد. قابل قبول است.
تهیه کننده : جابر عامری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم



1736019749.png)















