درسنامه کامل ریاضی هفتم فصل 9 آمار و احتمال
تعداد بازدید : 7.59Mخلاصه نکات ریاضی هفتم فصل 9 آمار و احتمال - درسنامه شب امتحان ریاضی هفتم فصل 9 آمار و احتمال - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 9 آمار و احتمال
انواع نمودار در علم آمار
علم آمار
علم آمار علم جمع آوری اطلاعات، سازماندهی و بررسی آنها است. اطلاعات، جمع آوری شده را «داده های آماری» می گویند.
نمودار در علم آمار
برای مقایسه و بررسی بهتر داده های آماری از انواع «نمودارها» استفاده می کنند. هر نمودار با توجه به موضوعی که داده های آن جمع آوری شده است و نوع اطلاعات به دست آمده، کارایی دارد.
انواع نمودارها و تفسیر نتیجه ها
1- نمودار میله ای:
نمودار میله ای برای مقایسه تعداد پیدا کردن بیشترین و کمترین داده به کار می رود.
در حال حاضر نرم افزارهای زیادی برای رسم انواع نمودار ها وجود دارند.
آنچه اهمیت دارد رسم نمودار نیست، بلکه انتخاب نمودار مناسب برای موضوع مورد نظر است.
مثال
مدت زمانی که طول می کشد تا کارگران یک کار خانه از خانه به محل کار بروند، در نمودار مقابل نشان داده شده است. با توجه به این نمودار، فاصله زمانی خانۀ چند کارگر تا محل کار بیشتر از 10 دقیقه است؟
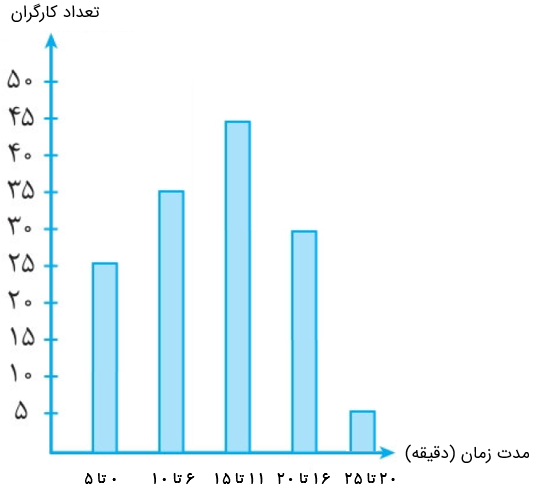
ابتدا ستون هایی را مشخص می کنیم که زمان بیشتر از 10 دقیقه را نشان می دهند (ستون های سوم، چهارم و پنجم):
45 نفر : ستون سوم (11 تا 15 دقیقه)
30 نفر : ستون چهارم (16 تا 20 دقیقه)
5 نفر : ستون پنجم (20 تا 25 دقیقه)
نفر 80 = 5 + 30 + 45 = تعداد کارگرانی که فاصله خانه تا محل کار بیشتر از 10 دقیقه است
2- نمودار خط شکسته:
نمودار خط شکسته برای نمایش تغییرها کاربرد دارد؛ بنابراین در موضوع هایی که تغییرها اهمیت دارد، از این نمودار استفاده می شود.
برای نمونه، تغییرها در بازارهای مالی، قیمت طلا، نفت، سهام و ... را با این نمودار نشان می دهند.
گاهی وقت ها به جای داده های واقعی از مقدار تقریبی آنها استفاده می کنیم. در برنامه ریزی های کلان به عددهای واقعی و دقیق نیاز نداریم.
برای مثال مقدار تولید گندم یک استان را به صورت چند هزار تن بیان می کنند؛ یعنی مقدار کمتر از ۱۰۰۰ تن یا یک میلیون کیلوگرم در این بررسی اهمیت ندارد.
مثال
در نمودار خط شکسته زیر، بیشترین تغییرات دما بین کدام یک از ماه های سال است؟
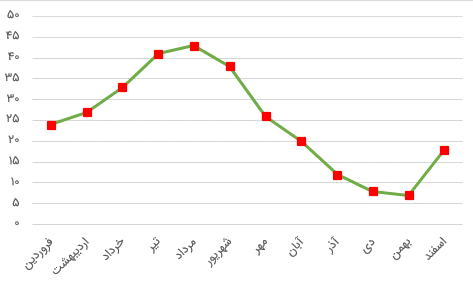
در نمودار خط شکسته، وقتی شیب خطی بیشتر باشد، یعنی تغییرات در آن قسمت ها بیشتر از بقیه قسمت هاست. در نمودار بالا بین دو ماه شهریور و مهر و دو ماه بهمن و اسفند تغییرات دمایی بالایی است؛ حال بین این دو تغییرات یکی از تغییرات بیشترین خواهد بود:
10 = 7 – 17 = تغییرات دمایی بین دو ماه شهریور و مهر
13 = 25 – 38 = تغییرات دمایی بین دو ماه بهمن و اسفند
3- نمودار دایره ای:
بعضی از داده ها و اطلاعات جمع آوری شده نشان می دهد که یک مقدار مشخص به چه نسبتی به بخش های کوچک تر تقسیم شده است.
در این موارد می توان تقسیم شدن را روی یک شکل مثل دایره نشان داد و سهم هر بخش را روی دایره مشخص کرد.
در نمودار دایره ای به طور معمول نسبت و سهم هر بخش را به صورت درصد محاسبه کرده و سپس روی نمودار نمایش می دهند.
مثال
نمودار دایره ای مقابل مربوط به محصولات یک مزرعه است. اگر میزان کل محصولات 180 تن باشد، میزان محصولات این مزرعه را مشخص کنید.
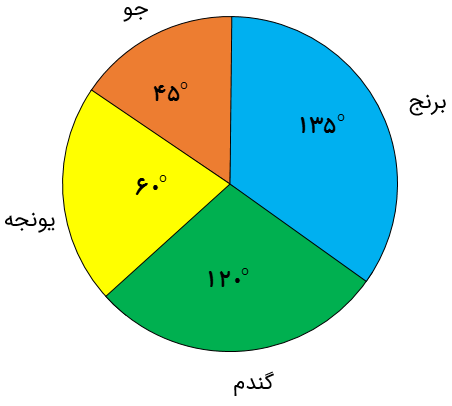
تن \(\, = \,\frac{{{{135}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 67/5\) میزان برنج
تن\(\, = \,\frac{{{{45}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 22/5\) میزان جو
تن\(\, = \,\frac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 30\) میزان یونجه
میزان گندم\(\, = \,\frac{{{{120}^ \circ }}}{{{{360}^ \circ }}} \times 180 = 60\)تن
4- نمودار تصویری:
گاهی وقت ها به جای داده های واقعی از مقدار تقریبی آنها استفاده می کنیم. در برنامه ریزی های کلان به عدد های واقعی و دقیق نیاز نداریم؛ برای مثال مقدار تولید گندم یک استان را به صورت چند هزار تن بیان می کنند، یعنی مقدار کمتر از ۱۰۰۰ تن یا یک میلیون کیلوگرم در این بررسی اهمیت ندارد.
ابتدا مقدار تقریبی هر عدد را با تقریب کمتر از مقدار مورد نظر گرد کنید. سپس با رسم یک شکل برای تعدادی مشخص، نمودار تصویری آن را رسم کنید.
مثال
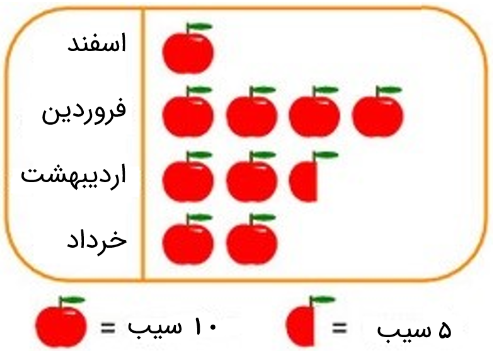
اگر هر شکل سیب کامل رو به عنوان 10 عدد سیب در نظر بگیریم، و فردی میزان فروش سیب را در ماه های اسفند تا خرداد به صورت زیر ثبت کرده باشد، نمودار تصویری این برنامه فروش را رسم کنید.
در اسفند، 10 سیب فروخته شد.
در فروردین، 40 سیب فروخته شد.
در اردیبهشت 25 سیب فروخته شد.
در خرداد 20 سیب فروخته شد.
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
دسته بندی داده ها (فراوانی،میانگین)
دسته بندی داده ها
اگر داده های جمع آوری شده زیاد و پراکنده باشند بررسی آنها طولانی می شود. برای اینکه بتوانیم آسان تر و بهتر نتیجه بگیریم، داده ها را متناسب با موضوع آماری دسته بندی و سازماندهی می کنیم.
دامنه تغییرات در داده های آماری
به فاصله بین کمترین و بیشترین داده، «دامنه تغییرات» می گویند.
مثال
دامنه تغییرات داده های آماری زیر را بیابید.
10، 15، 13، 21، 18، 23، 8، 1، 30، 31، 15، 10، 8، 7، 12، 11
ابتدا کمترین داده و بیشترین داده را مشخص می کنیم:
1 = کمترین داده
31 = بیشترین داده
30 = 1 – 31 = دامنه تغییرات
فراوانی
تعداد داده های هر دسته را «فراوانی» می گویند. فراوانی را به دو صورت زیر می توان نشان داد:
۱) استفاده از چوب خط
۲) استفاده از عدد
مثال
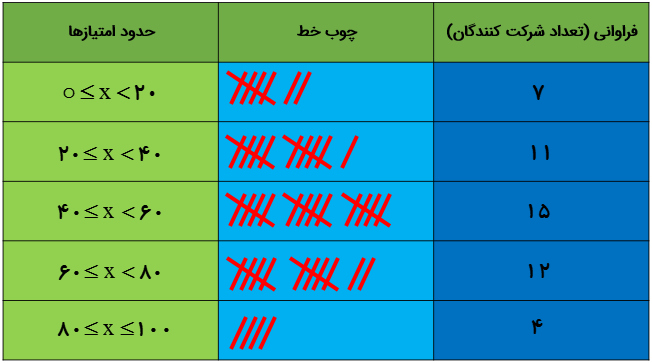
جدول زیر، امتیازهای شرکت کنندگان یک آزمون 100 نمره ای را نشان می دهد. ابتدا ستون فراوانی را بر اساس ستون چوب خط کامل کنید؛ سپس محاسبه کنید که امتیاز چند نفر بیشتر از 60 می باشد.
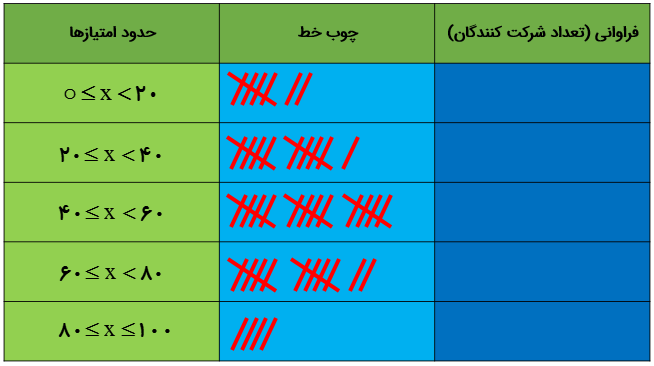
16 = 4 + 12 = تعداد شرکت کنندگانی که امتیاز بالای 60 گرفته اند
میانگین داده ها
پس از اینکه داده های آماری در جدول سازماندهی می شوند و به کمک نمودارها درک بهتری از داده ها به دست آمد، می توان از میانگین داده ها برای کامل تر شدن نتایج حاصل از داده ها و تحلیل و تفسیر بهتر آنها استفاده کرد. میانگین تعدادی داده از تقسیم مجموع آنها بر تعدادشان به دست می آید:
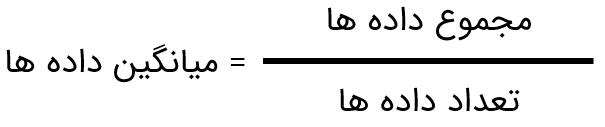
به صورت جبری:
\(\overline x = \frac{s}{n}\)
اگر تعداد داده ها زیاد باشد و داده ها دسته بندی شده باشند، می توان میانگین داده ها را با تقریب بسیار خوب به دست آورد.
مثال
اگر نمودار تغییرات دمایی یک منطقه در 24 ساعت در نمودار زیر آمده باشد، میانگین دمایی این منطقه را بدست آورید.
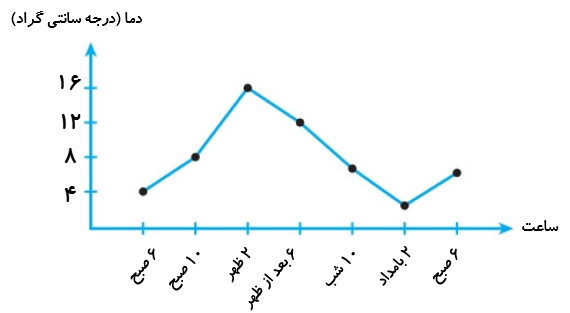
همه دماهای مشخص شده را جمع می بندیم و بر تعداد نقطه ها تقسیم می کنیم:
میانگین دمای منطقه\(\,\, = \frac{{4 + 8 + 16 + 12 + 8 + 4 + 8}}{7} = \frac{{60}}{7} \simeq 8/6\)درجه سانتی گراد
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
احتمال یا اندازه گیری شانس
احتمال یا اندازه گیری شانس
وقتی یک سکه را می اندازیم دو حالت هم شانس ممکن است اتفاق بیفتد، یا سکه رو می آید یا پشت و چون در یک حالت از این دو حالت ممکن، سکه رو می آید، پس احتمال رو آمدن سکه \(\frac{1}{2}\) است.
به این ترتیب برای بیان اندازه شانس رخ دادن یک اتفاق، از یک عدد استفاده کرده ایم که «احتمال رخ دادن» آن اتفاق نامیده می شود.
برای اینکه احتمال رخ دادن یک اتفاق را به دست آوریم، ابتدا همۀ حالت های ممکن را می یابیم، سپس حالت های مورد نظر را از میان حالت های ممکن پیدا می کنیم. احتمال رخ دادن اتفاق مورد نظر برابر است با نسبت تعداد حالت های مورد نظر به تعداد حالت های ممکن؛ بنابراین احتمال رخ دادن یک اتفاق از دستور زیر به دست خواهد آمد:
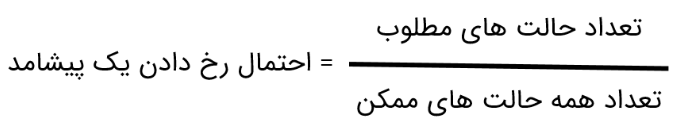
به عبارت دیگر برای اینکه احتمال رخ دادن یک پیشامد را بیابیم، تعداد حالت های منجر به آن اتفاق را بر تعداد کل حالت ها تقسیم می کنیم. احتمال روی دادن هر پیشامد را با یک کسر که بین صفر و یک می باشد، نشان می دهیم.
محاسبه n بار از انتظار یک پیشامد
از دستور زیر کمک می گیریم:
تعداد کل انجام کار × احتمال روی دادن اتفاق
مثال
تاسی را ۶۰ بار پرتاب می کنیم. انتظار داریم چند بار عدد ۴ بیاید؟
\(\frac{1}{6} \times 60 = 10\)
مثال
تمام پیشامدهای ممکن از پرتاب دو سکه را بنویسید.
رو آمدن سکه را با R و پشت آمدن آن را با P نشان می دهیم:
تمام پیشامدهای ممکن از پرتاب دو سکه\( = \left\{ {(R\,,\,R)\,,\,(R\,,\,P)\,,\,(P\,,\,R)\,,\,(P\,,\,P)} \right\}\)
(R ، P) یعنی اینکه سکه اول پشت بیاید و سکه دوم رو ظاهر شود.
مثال
احتمال رخ دادن پیشامد اینکه در پرتاب دو سکه، هر دو سکه پشت ظاهر شوند را بیابید.
پیشامد پشت ظاهر شدن دو سکه\(\,\, = \left\{ {(P\,,\,P)} \right\}\)
تمام پیشامدهای ممکن\(\,\, = \left\{ {(R\,,\,R)\,,\,(R\,,\,P)\,,\,(P\,,\,R)\,,\,(P\,,\,P)} \right\}\)
احتمال\( = \frac{1}{4}\)
مثال
یک سکه و یک تاس را هم زمان به آسمان پرتاب می کنیم. تمام پیشامدهای ممکن را نوشته و محاسبه کنید که چقدر احتمال دارد که بر روی تاس عدد زوج ظاهر شود و سکه نیز رو ظاهر شود؟
رو آمدن سکه را با R و پشت آمدن آن را با P نشان می دهیم:
تمام پیشامدهای ممکن\(\,\, = \left\{ \begin{array}{l}(R\,,\,1)\,,\,(R\,,\,2)\,,\,(R\,,\,3)\,,\,(R\,,\,4)\,,\,(R\,,\,5)\,,\,(R\,,\,6)\,,\,\\(P\,,\,1)\,,\,(P\,,\,2)\,,\,(P\,,\,3)\,,\,(P\,,\,4)\,,\,(P\,,\,5)\,,\,(P\,,\,6)\end{array} \right\}\)
تعداد تمام حالت های ممکن 12 می باشد.
پیشامد تاس زوج و سکه رو\(\,\, = \left\{ {(R\,,\,2)\,,\,(R\,,\,4)\,,\,(R\,,\,6)} \right\}\)
تعداد این پیشامد نیز 3 می باشد. در نتیجه:
احتمال\( = \frac{3}{{12}} = \frac{1}{4}\)
تهیه کننده:مسعود زیرکاری
روش های نوشتن کل حالات پیشامد
مجموع روی دادن و روی ندادن یک پیشامد
مجموع احتمال روی دادن و احتمال روی ندادن یک اتفاق همیشه برابر با عدد ۱ است.
روش های نوشتن کل حالت های یک پیشامد
برای این کار از دو روش زیر کمک می گیریم:
1- جدول نظام دار:
جدول نظام دار برای حالتی مناسب که دو رویداد را مورد بررسی قرار دهیم. در این روش حالت های یک رویداد را افقی و حالت های رویداد بعدی را عمودی نوشته و مانند جدول ضرب، سایر خانه ها را پر می کنیم.
۲- نمودار درختی:
در روش نمودار درختی، برای هر حالت یک شاخه در نظر گرفته و در انتهای هر شاخه حالت های پیشامد بعدی را می نویسیم. روش نمودار درختی می تواند بهترین روش برای محاسبه همه حالت های رخداد یک پیشامد باشد.
مثال
تمام پیشامدهای ممکن از پرتاب سه تا سکه را به صورت جدول نظام دار و نمودار درختی نمایش دهید.
نمایش به صورت جدول نظام دار:
|
جدول نظام دار |
||
|
سکه اول |
سکه دوم |
سکه سوم |
|
رو |
رو |
رو |
|
رو |
رو |
پشت |
|
رو |
پشت |
رو |
|
رو |
پشت |
پشت |
|
پشت |
رو |
رو |
|
پشت |
رو |
پشت |
|
پشت |
پشت |
رو |
|
پشت |
پشت |
پشت |
نمایش به صورت نمودار درختی:
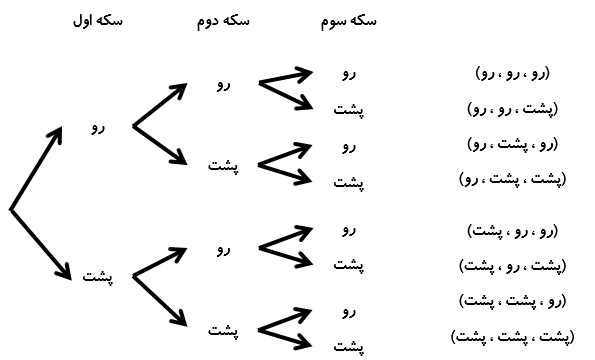
البته نوع دیگری از نمایش جدول نظام دار برای همین مثال به صورت زیر است:
|
جدول نظام دار |
||
|
سکه اول |
سکه دوم |
سکه سوم |
|
رو |
رو |
رو |
|
پشت |
||
|
پشت |
رو |
|
|
پشت |
||
|
پشت |
|
رو |
|
رو |
پشت |
|
|
پشت |
رو |
|
|
پشت |
||
مثال
تمام پیشامدهای ممکن از پرتاب یک سکه و یک تاس را به صورت جدول نظام دار و نمودار درختی نمایش دهید.
نمایش به صورت جدول نظام دار:
|
جدول نظام دار |
|
|
تاس |
سکه |
|
1 |
رو |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
1 |
پشت |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
نمایش به صورت نمودار درختی:
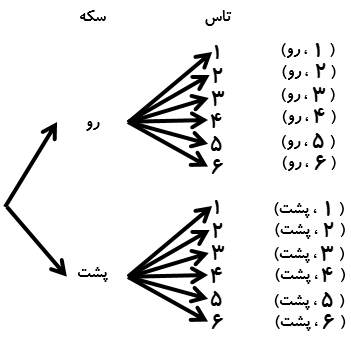
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم



1736019749.png)















