تابع \(y = \frac{{ - 1}}{{10}}{x^2} + 0/63{x^3} - 3\frac{1}{4}{x^5}\) یک تابع چند جمله ای از درجه ........... است.
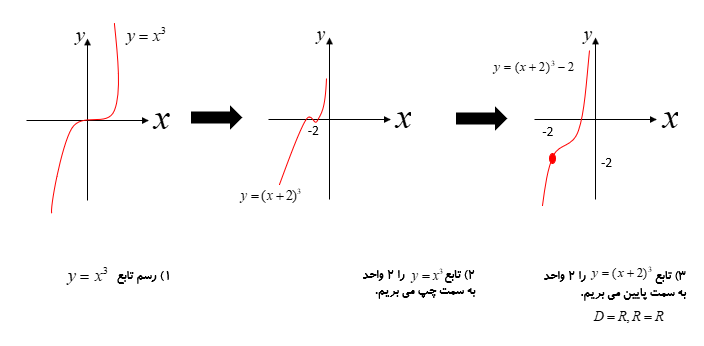
تابع \(f(x) = {(x + 2)^3} - 2\) را به کمک نمودار \(y = {x^3}\) رسم کرده و دامنه و برد آن را بدست آورید.
ابتدا نمودار تابع \(f(x) = \left\{ {\begin{array}{*{20}{c}}{{{(x + 1)}^2}}&,&{x \ge 0}\\{2x + 1}&,&{ - 2 \le x < 0}\\{ - 3}&,&{x < - 2}\end{array}} \right.\) را رسم کرده و سپس صعودی و نزولی بودن تابع در هر بازه را بررسی کنید.
حدود تغییرات \(a\) را طوری بیابید که تابع \(f = \left\{ {(1,{a^2}),( - 3, - 3a + 1),( - 1,2a)} \right\}\) صعودی باشد.
در شرط تشکیل تابع مرکب \(gof\) باید ............. تابع \(f\) با ............. تابع \(g\) اشتراک داشته باشد.
توابع \(f = \left\{ {( - 3,2),(4,5),( - 1, - 2)} \right\}\) و \(g = \left\{ {(5,1),(2, - 2),(7, - 1)} \right\}\) مفروض اند، fog و gof را بدست آورید.
اگر \(f(x) = \sqrt {3x - 2} \) و \(g(x) = \frac{2}{{2x - 1}}\)، آنگاه ضابطه تابع fog را به همراه دامنه آن بدست آورید.
اگر \(f(x) = 3x + 1\) و \(gog(x) = \frac{{x + 1}}{{x - 1}}\)، آنگاه ضابطه \(g(x)\) را به دست آورید.
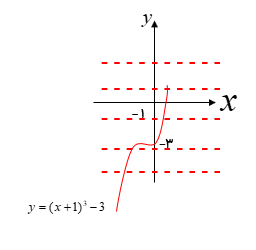
یک به یک بودن تابع \(y = {(x + 1)^3} - 3\) را بررسی کرده و در صورت یک به یک بودن ضابطه تابع وارون ان را به دست آورید.
محدوده یک به یک بودن تابع \(y = {(x - 2)^2}\) را بدست آورید.
اگر تابع \(g = \{ (3, - 1),(0,2),( - 5,1)\} ,f = \{ ( - 1,10),(0, - 2),(3,2)\} \) باشد، آنگاه \(fo{g^{ - 1}},go{g^{ - 1}}\) را بدست آورید.
اگر \(g(x) = {x^3} - 3,f(x) = 5x + 3\) ، آنگاه مقدار \({g^{ - 1}}o{f^{ - 1}}(3)\) را به دست آورید.
اگر \(f(x) = 2{x^3} - 1\) باشد، حاصل \({f^{ - 1}}(15)\) برابر ................ است.
ضابطه تابع وارون \(y = {x^3}\)، برابر ................. است.
اگر \(g(x) = \sqrt {x + 3} ,f(x) = 7 - 4{x^2}\) باشد :
الف) دامنه تابع \(fog\) را با استفاده از تعریف بدست آورید.
ب) مقدار \((gof)(1)\) را محاسبه کنید.
اگر \(g = \{ (1,2),(3, - 1),(9,0),( - 1,4),(7,7)\} ,f = \{ (0, - 1),(5,9),(3,7),( - 2,4)\} \)، تابع \(gof\) را در صورت وجود بنویسید.
اگر \(f = \{ (2,3),(3,5)\} \) باشد، حاصل \({f^{ - 1}}(3)\) برابر .................. است.
اگر ورودی ماشین مقابل 3 یاشد، مقدار خروجی آن چقدر است؟
ورودی \(x \to 2x - 2 \to \frac{x}{{\sqrt x + 1}} \to \) خروجی
نمودار تابع \(f(x) = {x^3}\) در بازه \((0,1)\)، .............. از نمودار تابع \(g(x) = {x^2}\) قرار دارد.
اگر \(g(x) = 2{x^2} - 1\,,\,f(x) = \sqrt {x - 1} \) باشد،
الف) دامنه تابع \(fog\) را با استفاده از تعریف بدست آورید.
ب) مقدار \(gof(2)\) را تعیین کنید.
اگر \(fog(x) = \frac{1}{x}\,,\,f(x) = \frac{{2x}}{{1 - x}}\) باشد، ضابطه \(g(x)\) برابر است با ...................... .
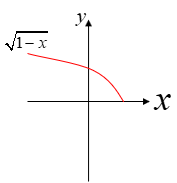
تابع \(y = \sqrt {1 - x} \) در دامنه تعریف خود، .................. است.
تابع \(f(x) = {(\frac{1}{3}{x^2} + 5)^2}\) به صورت ترکیب دو تابع \(g(x) = \frac{1}{3}{x^2} + 5\) و ................ \(h(x) = \) است.
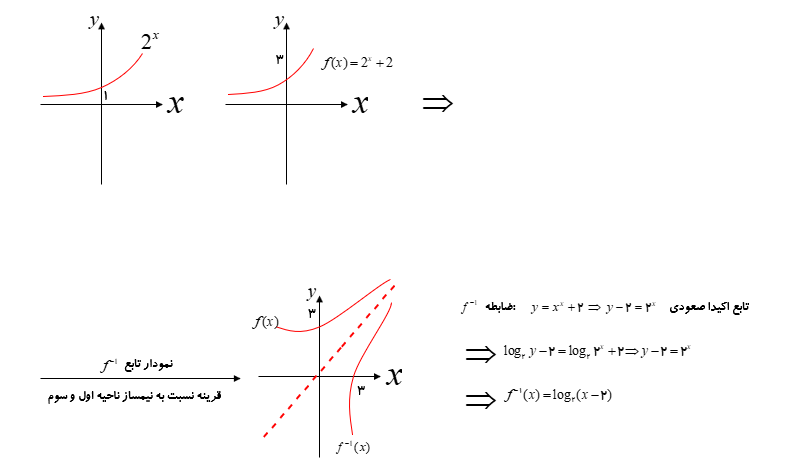
با رسم نمودار، وضعیت یکنوایی تابع \(f(x) = {2^x} + 2\) را بررسی کنید و در صورت امکان، ضابطه و نمودار تابع وارون آن را به دست آورید.
اگر \(g(x) = \sqrt {1 - x} \,,\,f(x) = \frac{{1 + {x^2}}}{{1 - {x^2}}}\)، ضابطه و دامنه تابع \(fog\) را به دست آورید.
اگر تابع \(f(x) = {x^2} + 2 + 2x\) باشد، آنگاه تابع \(g(x)\) را به گونه ای بدست آورید که رابطه \(fog(x) = {x^2} - 4x + 5\) برقرار باشد.
تابع \(y = {x^2}|x|\) در بازه \(( - \infty ,M)\) نزولی است. حداکثر مقدار M چقدر است؟
اگر \(g(x) = 1 - {x^2}\,,\,f(x) = 2 - \sqrt x \) آن گاه ضابطه \({g^{ - 1}}o{f^{ - 1}}\) را به دست آورید.
آیا دو تابع \(g(x) = \frac{1}{{x - 3}}\,,\,f(x) = \frac{1}{x} + 3\) وارون یکدیگرند؟



1736019749.png)