جواب تمرین صفحه 9 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 84.83Mپاسخ تمرین صفحه 9 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 9 درس هندسۀ تحلیلی و جبر
-تمرین صفحه 9 درس 1
-شما در حال مشاهده جواب تمرین صفحه 9 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 وضعیت هر جفت از خطوط زیر را نسبت به هم مشخص کنید:
\(\begin{array}{*{20}{l}}\begin{array}{l}L:{\rm{ }}2x{\rm{ }}--{\rm{ }}y{\rm{ }} = {\rm{ }}1\\\end{array}\\\begin{array}{l}T:{\rm{ }}y{\rm{ }} = {\rm{ }}2x{\rm{ }}--{\rm{ }}3\\\end{array}\\{\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}2y{\rm{ }} = {\rm{ }}0}\end{array}\)
\(\begin{array}{l}L:\quad 2x - y = 1 \Rightarrow y = 2x - 1 \Rightarrow {m_L} = 2\\\\T:\quad y = 2x - 3 \Rightarrow {m_T} = 2\\\\\Delta :\quad x + 2y = 0 \Rightarrow y = - \frac{1}{2}x \Rightarrow {m_\Delta } = - \frac{1}{2}\\\\ \Rightarrow \left\{ \begin{array}{l}{m_L} = {m_T}\\\\{m_L} \cdot {m_\Delta } = - 1\end{array} \right. \Rightarrow \quad \left\{ \begin{array}{l}L\parallel T\\\\L \bot \Delta \\\\T \bot \Delta \end{array} \right.\end{array}\)
2 دو نقطۀ A(14,3) و B(10,-13) را در نظر بگیرید. فاصلهٔ مبدأ مختصات را از وسط پاره خط AB به دست آورید.
\(\begin{array}{l}\left. \begin{array}{l}A\left( {14\;,\;3} \right)\\B\left( {10\;,\; - 13} \right)\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{14 + 10}}{2} = 12\\{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{3 + \left( { - 13} \right)}}{2} = - 5\end{array} \right. \Rightarrow M\left( {12\;,\; - 5} \right)\\O\left( {0\;,\;0} \right)\quad \Rightarrow OM = \sqrt {{{\left( {{x_M} - {x_O}} \right)}^2} + {{\left( {{y_M} - {y_O}} \right)}^2}} = \sqrt {{{\left( {12 - 0} \right)}^2} + {{\left( {\left( { - 5} \right) - 0} \right)}^2}} = \sqrt {169} = 13\end{array}\)
3 نشان دهید مثلث با رأس های A(1,2)، B(2,5) و C(4,1) یک مثلث متساوی الساقینِ قائم الزاویه است.
\(\begin{array}{l}\left. \begin{array}{l}A\left( {1\;,\;2} \right)\\B\left( {2\;,\;5} \right)\\C\left( {4\;,\;1} \right)\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {2 - 5} \right)}^2}} = \sqrt {1 + 9} = \sqrt {10} \\AC = \sqrt {{{\left( {{x_A} - {x_C}} \right)}^2} + {{\left( {{y_A} - {y_C}} \right)}^2}} = \sqrt {{{\left( {1 - 4} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = \sqrt {9 + 1} = \sqrt {10} \end{array} \right. \Rightarrow AB = AC\quad \left( i \right)\\\left\{ \begin{array}{l}{m_{AB}} = \frac{{{y_A} - {y_B}}}{{{x_A} - {x_B}}} = \frac{{2 - 5}}{{1 - 2}} = 3\\{m_{AC}} = \frac{{{y_A} - {y_C}}}{{{x_A} - {x_C}}} = \frac{{2 - 1}}{{1 - 4}} = - \frac{1}{3}\end{array} \right. \Rightarrow {m_{AB}} \cdot {m_{AC}} = - 1 \Rightarrow AB \bot AC\quad \left( {ii} \right)\\\mathop \Rightarrow \limits^{\left( i \right)\;,\;\left( {ii} \right)} \end{array}\)
مثلث ABC متساوی الساقین قائم الزاویه است
4 دو انتهای یکی از قطرهای دایره ای نقاط A(2,-2) و B(6,2) هستند.
الف اندازهٔ شعاع و مختصات مرکز دایره را بیابید.
ب آیا نقطۀ C(7,3) بر روی محیط این دایره قرار دارد؟ چرا؟
الف
\(\begin{array}{l}A\left( {2\;,\; - 2} \right)\\\\B\left( {6\;,\;4} \right)\\\\ \Rightarrow 2r = AB = \\\\\sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \\\\\sqrt {{{\left( {2 - 6} \right)}^2} + {{\left( {\left( { - 2} \right) - 4} \right)}^2}} = \\\\\sqrt {16 + 36} = \sqrt {52} = 2\sqrt {13} \end{array}\)
شعاع دایره \( \Rightarrow r = \sqrt {13} \)
\(\left\{ \begin{array}{l}{x_O} = \frac{{{x_A} + {x_B}}}{2} = \frac{{2 + 6}}{2} = 4\\\\{y_O} = \frac{{{y_A} + {y_B}}}{2} = \frac{{ - 2 + 4}}{2} = 1\end{array} \right.\)
ب برای اینکه بفهمیم این نقطه بر روی محیط دایره قرار دارد، بایستی فاصله آن را نسبت به مرکز دایره بدست آوریم. اگر برابر با شعاع دایره باشد، این نقطه روی محیط دایره قرار دارد:
\(\begin{array}{l}\overline {CO} = \sqrt {{{\left( {{x_O} - {x_C}} \right)}^2} + {{\left( {{y_O} - {y_C}} \right)}^2}} = \\\\\sqrt {{{\left( {4 - 7} \right)}^2} + {{\left( {1 - 3} \right)}^2}} = \\\\\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 2} \right)}^2}} = \\\\\sqrt {9 + 4} = \sqrt {13} \end{array}\)
چون فاصله نقطه C از مرکز دایره یعنی O برابر با شعاع دایره هست، بنابراین بر روی محیط دایره واقع شده است.
5 نقاط A(2,3)، B(-1,0) و C(1,-2) سه رأس از مستطیل ABCD هستند. مختصات رأس چهارم آن را بیابید. (با دانستن این مطلب که در هر مستطیل، قطرها منصف یکدیگرند، آیا می توانید راه حل کوتاه تری برای مسئله ارائه کنید؟)
محل برخورد قطرها را M می نامیم و مختصات آن را با داشتن دو سر پاره خط AC به دست می آوریم. اکنون می دانیم که نقطه M وسط قطر دیگر هم هست؛ بنابراین به کمک فرمول می توانیم مختصات رأس D را بدست آوریم :
\(\begin{array}{l}MA = MC \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_C}}}{2} = \frac{{2 + 1}}{2} = \frac{3}{2}\\{y_M} = \frac{{{y_A} + {y_C}}}{2} = \frac{{3 + \left( { - 2} \right)}}{2} = \frac{1}{2}\end{array} \right. \Rightarrow M\left( {\frac{3}{2}\;,\;\frac{1}{2}} \right)\\MB = MD \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_B} + {x_D}}}{2} \Rightarrow {x_D} = 2{x_M} - {x_B} = 4\\{y_M} = \frac{{{y_B} + {y_D}}}{2} \Rightarrow {y_D} = 2{y_M} - {y_B} = 1\end{array} \right. \Rightarrow D\left( {4\;,\;1} \right)\\\\\end{array}\)
راه حل کوتاه تر :
\(AD = BC \Rightarrow \left\{ \begin{array}{l}{x_D} - {x_A} = {x_C} - {x_B} \Rightarrow {x_D} - 2 = 2 \Rightarrow {x_D} = 4\\{y_D} - {y_A} = {y_C} - {y_B} \Rightarrow {y_D} - 3 = - 2 \Rightarrow {y_D} = 1\end{array} \right. \Rightarrow D\left( {4\;,\;1} \right)\)

6 یک میلهٔ پرچم بزرگ، مطابق شکل توسط کابل هایی به چهار نقطه در زمین محکم شده است؛ به طوری که فاصلهٔ هر یک از چهار نقطه تا پای میله برابر است با فاصلهٔ نقطهٔ مقابل آن تا پای میله. مختصات نقطهٔ D را به دست آورید.
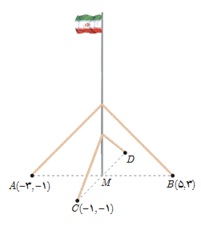
\(\begin{array}{l}MA = MB \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{ - 3 + 5}}{2} = 1\\{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{ - 1 + 3}}{2} = 1\end{array} \right. \Rightarrow M\left( {1\;,\;1} \right)\\MC = MD \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_C} + {x_D}}}{2} \Rightarrow {x_D} = 2{x_M} - {x_C} = 3\\{y_M} = \frac{{{y_C} + {y_D}}}{2} \Rightarrow {y_D} = 2{y_M} - {y_C} = 1\end{array} \right. \Rightarrow D\left( {3\;,\;3} \right)\end{array}\)
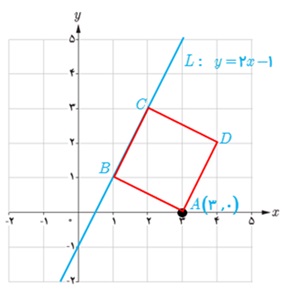
7 یکی از اضلاع مربعی بر خط L : y=2x-1 واقع است. اگر A(3,0) یکی از رئوس این مربع باشد، مساحت آن را به دست آورید.
نقطه A روی خط قرار ندارد، بنابراین از نقطه A بر خط L عمود می کنیم. فاصله این نقطه از خط، طول ضلع مربع است :
\(\left\{ \begin{array}{l}A\left( {3\;,\;0} \right) = \left( {{x_ \circ }\;,\;{y_ \circ }} \right)\\y = 2x - 1 \Rightarrow - 2x + y + 1 = 0\end{array} \right. \Rightarrow AB = \frac{{\left| {a{x_ \circ } + b{y_ \circ } + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| { - 2\left( 3 \right) + 1\left( 0 \right) + 1} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( 1 \right)}^2}} }} = \frac{5}{{\sqrt 5 }} = \sqrt 5 \)
\( \Rightarrow S = A{B^2} = {\left( {\sqrt 5 } \right)^2} = 5\)
8
الف نشان دهید دو خط با معادلات 5x–12y+8=0 و -10x+24y+10=0 با یکدیگر موازی اند.
ب فاصلهٔ این دو خط را محاسبه کنید.)راهنمایی: یک نقطهٔ دلخواه روی یکی از خطوط در نظر بگیرید و فاصلهٔ آن را از خط دیگر به دست آورید).

الف
\(\left\{ \begin{array}{l}L:\quad 5x - 12y + 8 = 0 \Rightarrow y = \frac{5}{{12}}x + \frac{2}{3} \Rightarrow {m_L} = \frac{5}{{12}}\\L':\quad - 10x + 24y + 10 = 0 \Rightarrow y = \frac{5}{{12}}x - \frac{5}{{12}} \Rightarrow {m_{L'}} = \frac{5}{{12}}\end{array} \right. \Rightarrow {m_L} = {m_{L'}} \Rightarrow L\parallel L'\)
ب
\(\left\{ \begin{array}{l}L:\quad 5x - 12y + 8 = 0 \Rightarrow A\left( {8,4} \right)\\L':\quad - 10x + 24y + 10 = 0\end{array} \right. \Rightarrow d = \frac{{\left| {a'{x_A} + b'{y_A} + c'} \right|}}{{\sqrt {{{a'}^2} + {{b'}^2}} }} = \frac{{\left| { - 10\left( 8 \right) + 24\left( 4 \right) + 10} \right|}}{{\sqrt {{{\left( { - 10} \right)}^2} + {{24}^2}} }} = \frac{{26}}{{26}} = 1\)
9 طول جغرافیایی تبریز تقریباً 46 درجهٔ شرقی و عرض جغرافیایی آن حدود 38 درجهٔ شمالی است. برای راحتی، می توانیم موقعیت این شهر را به طور خلاصه، به صورت (46,38) نشان دهیم. این اطلاعات دربارهٔ چابهار به صورت (61,45) است. با فرض اینکه مسافت فیزیکی هر درجه طول جغرافیایی همانند مسافت فیزیکی هر درجه عرض جغرافیایی برابر 110 کیلومتر باشد، مطلوب است محاسبهٔ فاصلهٔ تقریبی این دو شهر.

\(\begin{array}{l}\left. \begin{array}{l}A\left( {{{46}^ \circ }\;,\;{{38}^ \circ }} \right)\\B\left( {{{61}^ \circ }\;,\;{{25}^ \circ }} \right)\end{array} \right\} \Rightarrow AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \\\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}&{}&{}\end{array}\quad \; = \sqrt {{{\left( {46 - 61} \right)}^2} + {{\left( {38 - 25} \right)}^2}} = \sqrt {{{\left( { - 15} \right)}^2} + {{\left( {13} \right)}^2}} \simeq 19/{8^ \circ } \times 110 = 2178\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















