جواب تمرین صفحه 18 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 84.83Mپاسخ تمرین صفحه 18 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 18 درس هندسۀ تحلیلی و جبر
-تمرین صفحه 18 درس 1
-شما در حال مشاهده جواب تمرین صفحه 18 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 معادله های زیر را حل کنید.
الف \({x^4} - 8{x^2} + 8 = 0\)
ب \(4{x^6} + 1 = 5{x^3}\)
الف \({x^4} - 8{x^2} + 8 = 0 \Rightarrow t = {x^2} \Rightarrow {t^2} - 8t + 8 = 0 \Rightarrow \Delta = {\left( { - 8} \right)^2} - 4\left( 1 \right)\left( 8 \right) = 32\)
\(\begin{array}{l} \Rightarrow t = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{8 \pm \sqrt {32} }}{2}\\ \Rightarrow \left\{ \begin{array}{l}{t_1} = \frac{{8 - 4\sqrt 2 }}{2} = 4 - 2\sqrt 2 \Rightarrow {x^2} = 4 - 2\sqrt 2 \Rightarrow x = \pm \sqrt {4 - 2\sqrt 2 } \\{t_2} = \frac{{8 + 4\sqrt 2 }}{2} = 4 + 2\sqrt 2 \Rightarrow {x^2} = 4 + 2\sqrt 2 \Rightarrow x = \pm \sqrt {4 + 2\sqrt 2 } \end{array} \right.\end{array}\)
ب \(4{x^6} + 1 = 5{x^3} \Rightarrow t = {x^3} \Rightarrow 4{t^2} + 1 = 5t \Rightarrow 4{t^2} - 5t + 1 = 0 \Rightarrow \Delta = {\left( { - 5} \right)^2} - 4\left( 4 \right)\left( 1 \right) = 9\)
\(\begin{array}{l} \Rightarrow t = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{5 \pm \sqrt 9 }}{8}\\ \Rightarrow \left\{ \begin{array}{l}{t_1} = \frac{{5 - 3}}{8} = \frac{1}{4} \Rightarrow {x^3} = \frac{1}{4} \Rightarrow x = \frac{1}{{\sqrt[3]{4}}} = \frac{{\sqrt[3]{{16}}}}{4}\\{t_2} = \frac{{5 + 3}}{8} = 1 \Rightarrow {x^3} = 1 \Rightarrow x = 1\end{array} \right.\end{array}\)
2 معادلهٔ درجهٔ دومی بنویسید که ریشه های آن \(1 - \sqrt 2 \) و \(1 + \sqrt 2 \) باشد.
\(\begin{array}{l}\left. \begin{array}{l}\alpha = 1 - \sqrt 2 \\\beta = 1 + \sqrt 2 \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}S = \alpha + \beta = 1 - \sqrt 2 + 1 + \sqrt 2 = 2\\P = \alpha \cdot \beta = \left( {1 - \sqrt 2 } \right) \times \left( {1 + \sqrt 2 } \right) = {1^2} - {\left( {\sqrt 2 } \right)^2} = - 1\end{array} \right.\\ \Rightarrow {x^2} - Sx + P = 0 \Rightarrow {x^2} - 2x - 1 = 0\end{array}\)
3 مقدار ماکزیمم یا مینیمم توابع با ضابطه های زیر را به دست آورید.
الف \(f\left( x \right) = - 3{x^2} + 8x - 5\)
ب \(g\left( x \right) = 3{x^2} + 6x + 5\)
الف \(f\left( x \right) = - 3{x^2} + 8x - 5 \Rightarrow a = - 2 < 0\)
تابع دارای ماکزیمم است
\( \Rightarrow \left\{ \begin{array}{l}{x_S} = - \frac{b}{{2a}} = - \frac{8}{{2\left( { - 2} \right)}} = 2\\ \Rightarrow {y_S} = f\left( 2 \right) = - 2{\left( 2 \right)^2} + 8\left( 2 \right) - 5 = 3\end{array} \right. \Rightarrow S\left( {2\;,\;3} \right)\)
ب \(g\left( x \right) = 3{x^2} + 6x + 5 \Rightarrow a = 3 > 0\)
تابع دارای مینیمم است
\( \Rightarrow \left\{ \begin{array}{l}{x_S} = - \frac{b}{{2a}} = - \frac{6}{{2\left( 3 \right)}} = - 1\\ \Rightarrow {y_S} = g\left( { - 1} \right) = 3{\left( { - 1} \right)^2} + 6\left( { - 1} \right) + 5 = 2\end{array} \right. \Rightarrow S\left( { - 1\;,\;2} \right)\)
4 موشکی که به طور عمودی رو به بالا شلیک شده، t ثانیه پس از پرتاب در ارتفاع h متری از سطح زمین قرار می گیرد که معادلهٔ آن به صورت مقابل است. \(h\left( t \right) = 100t - 5{t^2}\;\;\left( {t \ge 0} \right)\)
الف چقدر طول می کشد تا موشک به بالاترین ارتفاع ممکن خود برسد؟
ب ارتفاع نقطهٔ اوج را بیابید.
پ چند ثانیه پس از پرتاب، موشک به زمین باز می گردد؟
الف
\(h\left( t \right) = 100t - 5{t^2}\quad \left( {t \ge 0} \right)\quad \Rightarrow {t_S} = - \frac{b}{{2a}} = - \;\frac{{100}}{{2\left( { - \;5} \right)}} = 10\)
ب
\({h_S} = h\left( {{t_S}} \right) = 100\left( {10} \right) - 5{\left( {10} \right)^2} = 1000 - 500 = 500\)
پ
\(h\left( t \right) = 100t - 5{t^2} = 0 \Rightarrow 5t\left( {20 - t} \right) = 0 \Rightarrow \left\{ \begin{array}{l}5t = 0 \Rightarrow t = 0\\20 - t = 0 \Rightarrow t = 20\end{array} \right.\)
0 ← غ ق ق
20← ق ق
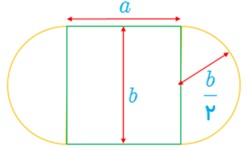
5 استادیومی به شکل مقابل درحال ساخت است که در آن x≥0 و y≥0 و نیم دایره ها به شعاع \(\frac{x}{2}\) هستند. اگر محیط استادیوم 1500 متر باشد، x و y را طوری بیابید که:

الف مساحت مستطیل حداکثر مقدار ممکن گردد.
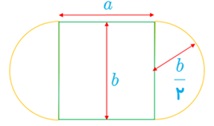
ب مساحت استادیوم حداکثر مقدار ممکن شود.
الف
ب
6 ضابطهٔ جبری سهمی های زیر را بنویسید.
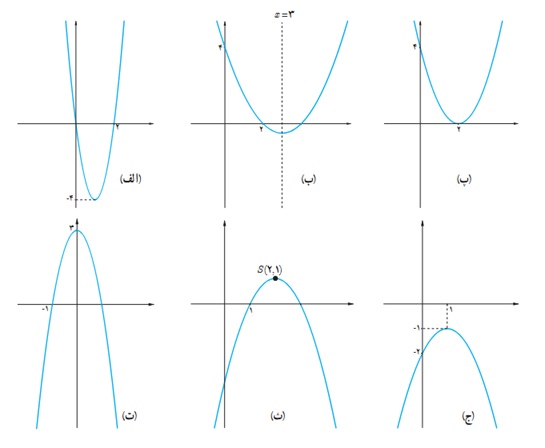
الف
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 0 \right) = 0 \Rightarrow c = 0\\f\left( 2 \right) = 0 \Rightarrow 4a + 2b = 0\\f\left( { - \frac{b}{{2a}}} \right) = - 4 \Rightarrow a{\left( { - \frac{b}{{2a}}} \right)^2} + b\left( { - \frac{b}{{2a}}} \right) = - 4\\ \Rightarrow \frac{{{b^2}}}{{4a}} - \frac{{{b^2}}}{{2a}} = - 4 \Rightarrow {b^2} = 16a\\\left\{ \begin{array}{l}{b^2} = 16a\\4a + 2b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{b^2} = 16a\\16a + 8b = 0\end{array} \right. \Rightarrow {b^2} + 8b = 0\\ \Rightarrow \left\{ \begin{array}{l}b = 0 \Rightarrow a = 0\\b = - 8 \Rightarrow a = 4\end{array} \right. \Rightarrow f\left( x \right) = 4{x^2} - 8x\end{array}\)
ب
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 0 \right) = 4 \Rightarrow c = 4\\f\left( 2 \right) = 0 \Rightarrow 4a + 2b + 4 = 0\\\left\{ \begin{array}{l}\frac{{ - \;b}}{{2a}} = 3\\4a + 2b + 4 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}6a + b = 0\\2a + b = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = - 3\end{array} \right.\\f\left( x \right) = \frac{1}{2}{x^2} - 3x + 4\end{array}\)
پ
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 0 \right) = 4 \Rightarrow c = 4\\f\left( 2 \right) = 0 \Rightarrow 4a + 2b + 4 = 0\\\left\{ \begin{array}{l}\frac{{ - \;b}}{{2a}} = 2\\4a + 2b + 4 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4a + b = 0\\2a + b = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 1\\b = - 4\end{array} \right.\\f\left( x \right) = {x^2} - 4x + 4\end{array}\)
ت
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 0 \right) = 3 \Rightarrow c = 3\\f\left( { - 1} \right) = 0 \Rightarrow a - b + 3 = 0\\\left\{ \begin{array}{l}\frac{{ - \;b}}{{2a}} = 0\\a - b + 3 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 0\\a - b = - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 3\\b = 0\end{array} \right.\\f\left( x \right) = - 3{x^2} + 3\end{array}\)
ث
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 1 \right) = 0 \Rightarrow a + b + c = 0\\f\left( 2 \right) = 0 \Rightarrow 4a + 2b + c = 1\\\frac{{ - \;b}}{{2a}} = 2 \Rightarrow \left\{ \begin{array}{l}4a + b = 0\\a + b + c = 0\\4a + 2b + c = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 3\\b = 4\\c = - 3\end{array} \right.\\f\left( x \right) = - 3{x^2} + 4x - 3\end{array}\)
ج
\(\begin{array}{l}f\left( x \right) = a{x^2} + bx + c\\f\left( 0 \right) = - 2 \Rightarrow c = - 2\\f\left( 1 \right) = - 1 \Rightarrow a + b - 2 = - 1\\\left\{ \begin{array}{l}\frac{{ - \;b}}{{2a}} = 1\\a + b - 2 = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = 2\\c = - 2\end{array} \right.\\f\left( x \right) = - \;{x^2} + 2x - 2\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















