جواب تمرین صفحه 87 درس 4 ریاضی یازدهم تجربی (مثلثات)
تعداد بازدید : 84.8Mپاسخ تمرین صفحه 87 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 87 درس مثلثات
-تمرین صفحه 87 درس 4
-شما در حال مشاهده جواب تمرین صفحه 87 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 حاصل هر یک از عبارت های زیر را به دست آورید:
الف \(tan135^\circ {\rm{ }} + {\rm{ }}cot120^\circ {\rm{ }} = \)
ب \(cos( - 210^\circ ){\rm{ }} + {\rm{ }}cot(240^\circ ){\rm{ }} = \)
پ \(sin630^\circ {\rm{ }} + {\rm{ }}tan( - 540^\circ ){\rm{ }} = \)
ت \(cos(-720°) + cot(-600°) + tan720° - tan(-600°) =\)
ث \(\sin \left( {\frac{{25\pi }}{3}} \right) - \cos \left( {\frac{{23\pi }}{4}} \right) = \)
ج \(\frac{{\sin \frac{{3\pi }}{4} - \cos \frac{{5\pi }}{6}}}{{\sin \left( {\frac{{ - 3\pi }}{4}} \right) + \tan \left( {\frac{{ - 4\pi }}{3}} \right)}} = \)
الف
\(\begin{array}{l}tan135^\circ {\rm{ }} + {\rm{ }}cot120^\circ {\rm{ }} = - 1 + \frac{{\sqrt 3 }}{3} = \frac{{\sqrt 3 - 3}}{3}\\\\\tan {135^ \circ } = \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right) = - \tan {45^ \circ } = - 1\\\\\cot {120^ \circ } = \cot \left( {{{180}^ \circ } - {{60}^ \circ }} \right) = - \cot {60^ \circ } = - \frac{{\sqrt 3 }}{3}\end{array}\)
ب
\(\begin{array}{l}cos\left( { - 210^\circ } \right){\rm{ }} + {\rm{ }}cot\left( {240^\circ } \right){\rm{ }} = - \frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{3} = - \frac{{\sqrt 3 }}{6}\\\\\cos \left( { - {{210}^ \circ }} \right) = \cos {210^ \circ } = \cos \left( {{{180}^ \circ } + {{30}^ \circ }} \right) = - \cos {30^ \circ } = - \frac{{\sqrt 3 }}{2}\\\\\cot {240^ \circ } = \cot \left( {{{180}^ \circ } + {{60}^ \circ }} \right) = \cot {60^ \circ } = \frac{{\sqrt 3 }}{3}\end{array}\)
پ
\(\begin{array}{l}sin630^\circ {\rm{ }} + {\rm{ }}tan\left( { - 540^\circ } \right){\rm{ }} = - 1 + 0 = - 1\\\\\sin {630^ \circ } = \sin \left( {2 \times {{360}^ \circ } - {{90}^ \circ }} \right) = \sin \left( { - {{90}^ \circ }} \right) = - \sin {90^ \circ } = - 1\\\\\tan \left( { - {{540}^ \circ }} \right) = - \tan {540^ \circ } = - \tan \left( {{{360}^ \circ } + {{180}^ \circ }} \right) = \\\\ - \tan {180^ \circ } = - \tan \left( {{{180}^ \circ } - {0^ \circ }} \right) = \tan {0^ \circ } = 0\end{array}\)
ت
\(\begin{array}{l}cos\left( { - 720^\circ } \right){\rm{ }} + {\rm{ }}cot\left( { - 600^\circ } \right){\rm{ }} + {\rm{ }}tan720^\circ {\rm{ }} - {\rm{ }}tan\left( { - 600^\circ } \right){\rm{ }} = \\\\1 - \frac{{\sqrt 3 }}{3} + 0 - \sqrt 3 = \frac{{3 - 4\sqrt 3 }}{3}\\\\\cos \left( { - {{720}^ \circ }} \right) = \cos {720^ \circ } = \cos \left( {2 \times {{360}^ \circ } + {0^ \circ }} \right) = \cos {0^ \circ } = 1\\\\\cot \left( { - {{600}^ \circ }} \right) = - \cot {600^ \circ } = - \cot \left( {2 \times {{360}^ \circ } - {{120}^ \circ }} \right) = \\\\ - \cot \left( { - {{120}^ \circ }} \right) = \cot {120^ \circ } = - \frac{{\sqrt 3 }}{3}\\\\\tan {720^ \circ } = \tan \left( {2 \times {{360}^ \circ } + 0} \right) = \tan {0^ \circ } = 0\\\\\tan \left( { - {{600}^ \circ }} \right) = - \tan {600^ \circ } = \\\\ - \tan \left( {2 \times {{360}^ \circ } - {{120}^ \circ }} \right) = - \tan \left( { - {{120}^ \circ }} \right) = \tan {120^ \circ } = - \sqrt 3 \end{array}\)
ث
\(\begin{array}{l}\sin \left( {\frac{{25\pi }}{3}} \right) - \cos \left( {\frac{{23\pi }}{4}} \right) = \frac{{\sqrt 3 }}{2} - \frac{{\sqrt 2 }}{2} = \frac{{\sqrt 3 - \sqrt 2 }}{2}\\\\\sin \left( {\frac{{25\pi }}{3}} \right) = \sin \left( {8\pi + \frac{\pi }{3}} \right)\\\\ = \sin \left( {4 \times 2\pi + \frac{\pi }{3}} \right) = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\\\cos \left( {\frac{{23\pi }}{4}} \right) = \cos \left( {6\pi - \frac{\pi }{4}} \right) = \cos \left( {3 \times 2\pi - \frac{\pi }{4}} \right)\\\\ = \cos \left( { - \frac{\pi }{4}} \right) = \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\end{array}\)
ج
\(\begin{array}{l}\frac{{\sin \frac{{3\pi }}{4} - \cos \frac{{5\pi }}{6}}}{{\sin \left( {\frac{{ - 3\pi }}{4}} \right) + \tan \left( {\frac{{ - 4\pi }}{3}} \right)}} = \frac{{\frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2}}}{{ - \frac{{\sqrt 2 }}{2} - \sqrt 3 }} = - \frac{{\sqrt 2 + \sqrt 3 }}{{\sqrt 2 + 2\sqrt 3 }}\\\\\sin \frac{{3\pi }}{4} = \sin \left( {\pi - \frac{\pi }{4}} \right) = \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\\\\\cos \frac{{5\pi }}{6} = \cos \left( {\pi - \frac{\pi }{6}} \right) = - \cos \frac{\pi }{6} = - \frac{{\sqrt 3 }}{2}\\\\\sin \left( { - \frac{{3\pi }}{4}} \right) = - \sin \frac{{3\pi }}{4} = - \frac{{\sqrt 2 }}{2}\\\\\tan \left( {\frac{{ - 4\pi }}{3}} \right) = - \tan \frac{{4\pi }}{3} = - \tan \left( {\pi + \frac{\pi }{3}} \right)\\\\ = - \tan \frac{\pi }{3} = - \sqrt 3 \end{array}\)
2 جدول زیر را کامل کنید:
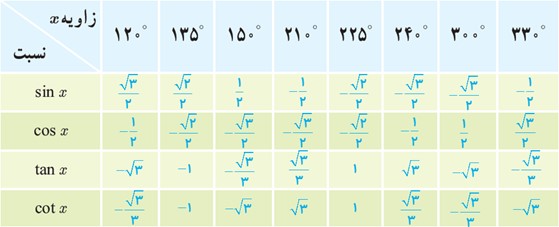
3 بدون استفاده از ماشین حساب درستی تساوی های زیر را بررسی کنید.
الف \(sin840^\circ {\rm{ }} = {\rm{ }}sin60^\circ \)
ب \(cos( - 324^\circ ){\rm{ }} = {\rm{ }}cos36^\circ \)
پ \(tan( - 1000^\circ ){\rm{ }} = {\rm{ }}tan80^\circ \)
ت \(sin875^\circ {\rm{ }} = {\rm{ }}sin155^\circ \;\)
الف
درست
\(\begin{array}{l}\sin {840^ \circ } = \sin \left( {{{720}^ \circ } + {{120}^ \circ }} \right) = \sin {120^ \circ }\\\\ = \sin \left( {{{180}^ \circ } - {{60}^ \circ }} \right) = \sin {60^ \circ } = \frac{{\sqrt 3 }}{2}\\\\\sin {60^ \circ } = \frac{{\sqrt 3 }}{2}\end{array}\)
ب
درست
ب
درست
\(\begin{array}{l}\cos \left( { - {{324}^ \circ }} \right) = \cos {324^ \circ }\\\\ = \cos \left( {{{360}^ \circ } - {{36}^ \circ }} \right) = \cos {36^ \circ }\end{array}\)
پ
درست
\(\begin{array}{l}\tan \left( { - {{1000}^ \circ }} \right) = - \tan {1000^ \circ }\\\\ = - \tan \left( {{{1080}^ \circ } - {{80}^ \circ }} \right) = \\\\ - \tan \left( {3 \times {{360}^ \circ } - {{80}^ \circ }} \right)\\\\ = - \tan \left( { - {{80}^ \circ }} \right) = \tan {80^ \circ }\end{array}\)
ت
درست
\(\sin {875^ \circ } = \sin \left( {{{720}^ \circ } + {{155}^ \circ }} \right) = \sin {155^ \circ }\)
4 در تساوی زیر به جای x یک زاویهٔ مناسب قرار دهید:
\(\sin x = \cos \left( {{{20}^\circ } + x} \right)\)
آیا برای زاویهٔ x تنها یک مقدار می توان یافت؟ جواب خود را با جواب های دوستان خود مقایسه کنید.
با توجه به رابطه نوشته شده، باید زوایا متمم هم باشند؛ بنابراین:
\(x + \left( {{{20}^ \circ } + x} \right) = {90^ \circ } \Rightarrow 2x = {70^ \circ } \Rightarrow x = {35^ \circ }\)
با توجه به رابطه نوشته شده، باید زوایا متمم هم باشند؛ بنابراین:
\(\begin{array}{l}\left( {x + \frac{\pi }{{18}}} \right) + \left( {\frac{{2\pi }}{9} + x} \right) = \frac{\pi }{2} \Rightarrow 2x + \frac{{5\pi }}{{18}} = \frac{\pi }{2}\\\\ \Rightarrow 2x = \frac{{4\pi }}{{18}} \Rightarrow x = \frac{\pi }{9}\end{array}\)
می توان زوایای بسیاری یافت که در تساوی های فوق صدق کنند؛ کافی است ضرایب π2 رادیان و یا 360 درجه را به این زوایا اضافه کرد؛ مثلا برای قسمت اول، 395درجه و برای قسمت دوم، \((2\pi + \frac{\pi }{9} = )\frac{{19\pi }}{9}\) رادیان جواب های دیگری هستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















