جواب تمرین صفحه 162 درس 7 ریاضی یازدهم تجربی (آمار و احتمال)

الف نادرست

ب نادرست

پ درست

ت درست

فرض کنیم انحراف معیار سن دانش آموزان کلاس باشد و میانگین فعلی سن افراد 16 سال باشد. در این صورت ضریب تغییرات فعلی برابر است با :

\(cv = \frac{\sigma }{{16}}\)

حال اگر 10 سال بگذرد، انحراف معیار تأثیرپذیر نمی باشد، ولی میانگین سنی افراد برابر 26 می شود؛ در نتیجه ضریب تغییرات سنی 10 سال آینده برابر است با :

\(\begin{array}{l}CV = \frac{\sigma }{{26}} \Rightarrow \\\\\frac{{CV}}{{cv}} = \frac{{\frac{\sigma }{{26}}}}{{\frac{\sigma }{{16}}}} = \frac{{16}}{{26}} = \frac{8}{{13}}\\\\ \Rightarrow CV = \frac{8}{{13}}cv\end{array}\)

بایستی ضریب تغییرات حقوق دریافتی هر شرکت را محاسبه کنیم. هر شرکت را که این مقدار برای آن بیشتر باشد، بی عدالت تر به نظر می رسد:

 \(\begin{array}{l}A:\;\;\:\left\{ {\begin{array}{*{20}{l}}{{x_1} = 1,200,000}\\{{x_2} = 1,600,000}\end{array}} \right.\\\\ \Rightarrow \bar X = \frac{{{x_1} + {x_2}}}{2} = 1,400,000\\\\\sigma _x^2 = \frac{\begin{array}{l}{\left( {1,200,000 - 1,400,000} \right)^2} + \\{\left( {1,600,000 - 1,400,000} \right)^2}\end{array}}{2}\\\\ \Rightarrow \sigma _x^2 = 4 \times {10^{10}}\\\\ \Rightarrow {\sigma _x} = 2 \times {10^5} = 200,000\\\\ \Rightarrow c{v_A} = \frac{{{\sigma _x}}}{{\bar X}} = \frac{{200,000}}{{1,400,000}} = \frac{1}{7}\\\\\\B:\;\;\:\left\{ {\begin{array}{*{20}{l}}{{y_1} = 2,500,000}\\{{y_2} = 3,000,000}\end{array}} \right.\\\\ \Rightarrow \bar Y = \frac{{{y_1} + {y_2}}}{2} = 2,750,000\\\\\sigma _y^2 = \frac{\begin{array}{l}{\left( {2,500,000 - 2,750,000} \right)^2} + \\{\left( {3,000,000 - 2,750,000} \right)^2}\end{array}}{2}\\\\ \Rightarrow \sigma _y^2 = 6/25 \times {10^{10}}\\\\ \Rightarrow {\sigma _y} = 2/5 \times {10^5} = 250,000\\\\ \Rightarrow c{v_B} = \frac{{{\sigma _y}}}{{\bar Y}} = \frac{{250,000}}{{2,750,000}} = \frac{1}{{11}}\end{array}\)

به نظر می رسد شرکت A بی عدالت تر باشد.

الف

\(\begin{array}{l}{{\bar X}_{Mina}} = \frac{{23 + 24 + 25 + 26 + 27}}{5} = 25\\\\{{\bar X}_{Maryam}} = \frac{{15 + 20 + 25 + 30 + 35}}{5} = 25\end{array}\)

ب

\(\begin{array}{l}\sigma _{Mina}^2 = \frac{\begin{array}{l}{\left( {23 - 25} \right)^2} + \\{\left( {24 - 25} \right)^2} + \\{\left( {25 - 25} \right)^2} + \\{\left( {26 - 25} \right)^2} + \\{\left( {27 - 25} \right)^2}\end{array}}{5} = 2\\\\ \Rightarrow {\sigma _{Mina}} = \sqrt 2 \\\\\\\sigma _{Maryam}^2 = \frac{\begin{array}{l}{\left( {15 - 25} \right)^2} + \\{\left( {20 - 25} \right)^2} + \\{\left( {25 - 25} \right)^2} + \\{\left( {30 - 25} \right)^2} + \\{\left( {35 - 25} \right)^2}\end{array}}{5} = 50\\\\ \Rightarrow {\sigma _{Maryam}} = 5\sqrt 2 \end{array}\)

پ برای مینا؛ زیرا پراکندگی پول توجیبی آن کمتر است.

ابتدا داده ها را از کوچک به بزرگ مرتب می کنیم: 

\(\begin{array}{l}10/4\:,\:10/8\:,\:11/9\:,\:11/9\:,\\\\\:12/4\:,\:\overbrace {\underbrace {15/6}_{}}^{}\:,\:18/4\:,\:21/5\:,\\\\\:25/4\:,\:30/5\:,\:34/7\;\;\:\\\\ \Rightarrow \:{Q_2} = 15/6\\\\\bar X = \frac{\begin{array}{l}10/4 + 10/8 + 11/9 + \\11/9 + 12/4 + 15/6 + \\18/4 + 21/5 + 25/4 + \\30/5 + 34/7\end{array}}{{11}}\\\\ \Rightarrow \bar X = \frac{{203/5}}{{11}} = 18/5\\\\{\sigma ^2} = \frac{{\begin{array}{*{20}{l}}\begin{array}{l}{\left( {10/4 - 18/5} \right)^2} + \\{\left( {10/8 - 18/5} \right)^2} + \\{\left( {11/9 - 18/5} \right)^2} + \\{\left( {11/9 - 18/5} \right)^2} + \end{array}\\\begin{array}{l}{\left( {12/4 - 18/5} \right)^2} + \\{\left( {15/6 - 18/5} \right)^2} + \\{\left( {18/4 - 18/5} \right)^2} + \\{\left( {21/5 - 18/5} \right)^2} + \end{array}\\\begin{array}{l}{\left( {25/4 - 18/5} \right)^2} + \\{\left( {30/5 - 18/5} \right)^2} + \\{\left( {34/7 - 18/5} \right)^2}\end{array}\end{array}}}{{11}}\\\\ \Rightarrow {\sigma ^2}\;\;\:{\mkern 1mu} = \frac{{677/14}}{{11}} \simeq 61/56\\\\ \Rightarrow \sigma \simeq 7/84\end{array}\)

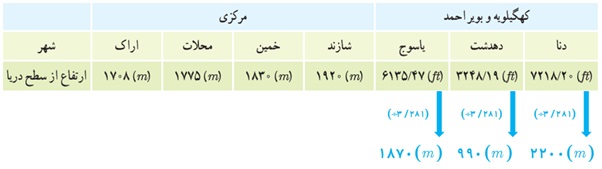
الف

\(\bar X = \frac{{1708 + 1775 + 1830 + 1920}}{4} \simeq 1808\)

ب

\(\begin{array}{l}{\sigma ^2} = \frac{\begin{array}{l}{\left( {1708 - 1808} \right)^2} + \\{\left( {1775 - 1808} \right)^2} + \\{\left( {1803 - 1808} \right)^2} + \\{\left( {1920 - 1808} \right)^2}\end{array}}{4}\\\\\;\;\:{\mkern 1mu} = \frac{\begin{array}{l}{\left( { - 100} \right)^2} + {\left( { - 33} \right)^2} + \\{\left( {22} \right)^2} + {\left( {112} \right)^2}\end{array}}{{}} \simeq 6029/25\\\\ \Rightarrow \sigma \simeq 77/64\end{array}\)

پ

 مرکزی  \(\bar X = \frac{{1708 + 1775 + 1830 + 1920}}{4} \simeq 1808\)

  کهگیلویه و بویر احمد \(\bar X = \frac{{1870 + 990 + 2200}}{3} \simeq 1686\)

شهرهای استان مرکزی  ارتفاع بیشتری نسبت سطح دریا دارند.