جواب فعالیت صفحه 91 درس 4 ریاضی یازدهم تجربی (مثلثات)
تعداد بازدید : 84.79Mپاسخ فعالیت صفحه 91 ریاضی یازدهم تجربی
-گام به گام فعالیت صفحه 91 درس مثلثات
-فعالیت صفحه 91 درس 4
-شما در حال مشاهده جواب فعالیت صفحه 91 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1
الف جدول زیر را کامل کنید.
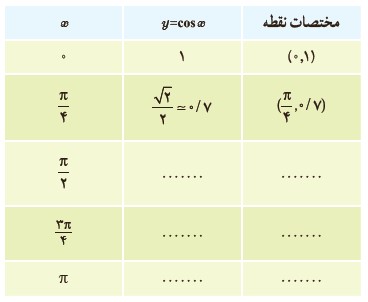
ب به این ترتیب مجموعه زوج های مرتب زیر به دست می آید.
\(f = \left\{ {\left( {0,1} \right)\;,\;\left( {......\;,\;......} \right)\;,\;\left( {......\;,\;......} \right)\;,\;\left( {......\;,\;......} \right)\;,\;\left( {......\;,\;......} \right)} \right\}\)
پ آیا این مجموعه یک تابع را مشخص می کند؟
الف
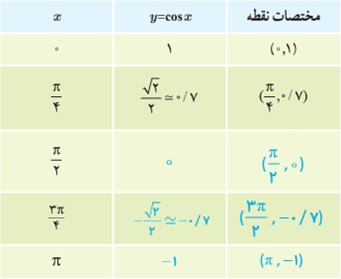
ب
\(f = \left\{ {\left( {0,1} \right)\;,\;\left( {\frac{\pi }{4}\;,\;0/7} \right)\;,\;\left( {\frac{\pi }{2}\;,\;0} \right)\;,\;\left( {\frac{{3\pi }}{4}\;,\; - 0/7} \right)\;,\;\left( {\pi \;,\; - 1} \right)} \right\}\)
پ
بله؛ یک تابع را مشخص می کند.
2 نقاط جدول بالا را در این شکل مشخص کنید.
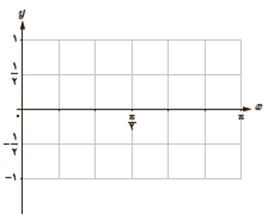
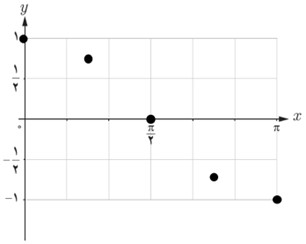
3 نقاط به طول های \(x = \frac{\pi }{6}\;,\;\frac{\pi }{3}\,,\;\frac{{2\pi }}{3}\;,\;\frac{{5\pi }}{6}\) را به جدول بالا اضافه کنید تا شکل زیر به دست آید.

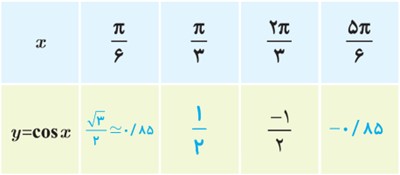
4 نقاط شکل صفحهٔ قبل را به ترتیب به یکدیگر وصل می کنیم تا شکل مقابل به دست آید. این شکل نمودار تابع کسینوس با ضابطه y=cosx را در بازۀ \([0,π] \) مشخص می کند.
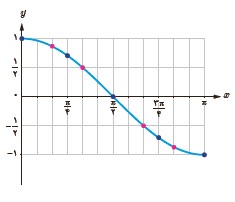
5 جدول زیر را کامل کنید تا نمودار تابع کسینوس در بازهٔ \([π,2π] \) به صورت شکل مقابل به دست آید.
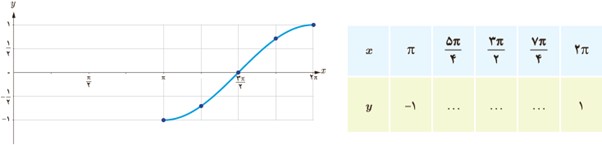
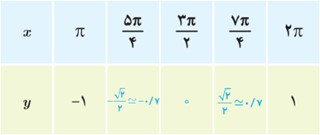
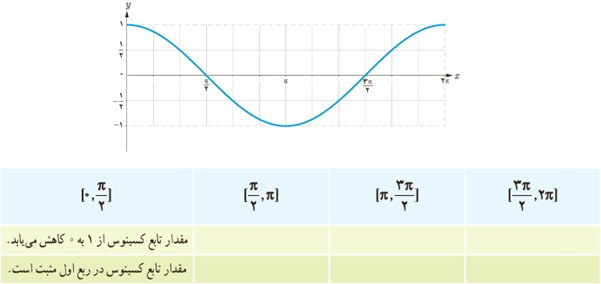
6 با توجه به مراحل بالا نمودار تابع کسینوس با ضابطهٔ y=cosx در بازهٔ \([0,2π] \) در شکل زیر رسم شده است. با توجه به این شکل جدول زیر را کامل کنید.

7 تابع کسینوس دارای نمودار یکسانی در بازه های \(\left[ { - 4\pi \;,\; - 2\pi } \right]\;,\;\left[ { - 2\pi \;,\;0} \right]\;,\;\left[ {2\pi \;,\;4\pi } \right]\;,\;\left[ {0\;,\;2\pi } \right]\) است. در شکل زیر نمودار تابع کسینوس در بازهٔ \([0,4π]\) رسم شده است. شکل را کامل کنید.


8 با توجه به شکل صفحهٔ قبل جاهای خالی را در خصوص ویژگی های تابع با ضابطهٔ y=cosx کامل کنید.
الف دامنهٔ تابع کسینوس ....... و برد آن ........ است.
ب مقدار تابع کسینوس در طول های .......... برابر با صفر است.
پ حداکثر مقدار تابع کسینوس ....... است که در طول های \(k \in Z\;,\;x = 2k\pi \) به دست می آید.
ت حداقل مقدار تابع کسینوس ...... است که در طول های ............ به دست می آید.
الف
\(\left[ { - 1\,,\,1} \right]\,\,\,\, - \,\,\,\,\mathbb{R}\)
ب
\(x = \frac{{\left( {2k - 1} \right)\pi }}{2}\)
پ
1
ت
1-
\(\left( {2k - 1} \right)\pi \)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















