جواب تمرین صفحه 10 درس 1 ریاضی نهم (مجموعه ها)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 10 ریاضی نهم
-گام به گام تمرین صفحه 10 درس مجموعه ها
-تمرین صفحه 10 درس 1
-شما در حال مشاهده جواب تمرین صفحه 10 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 مجموعه {2 ،1 ،0 ،1- ،2-} = A را درنظر بگیرید. کدامیک از مجموعه های زیر با هم برابر است؟
\(\begin{array}{l}B = \{ x|x \in A{\rm{ }},\,\,{x^2} \le 2\} \\\\C = \{ x|x \in A\,\,,\,\, - 1 \le x \le 1\} \\\\D = \left\{ {x|x \in A{\rm{ }},{x^4} = 1} \right\}\end{array}\)
با توجه به {2 ،1 ،0 ،1- ،2-} = A داریم:
\(\begin{array}{l}B = \{ x|x \in A,{\mkern 1mu} {\mkern 1mu} {x^2} \le 2\} \\\\x = - 2 \Rightarrow {( - 2)^2} = 4 \Rightarrow 4 > 2 \Rightarrow - 2 \notin B\\\\x = - 1 \Rightarrow {( - 1)^2} = 1 \Rightarrow 1 \le 2 \Rightarrow - 1 \in B\\\\x = 0 \Rightarrow {(0)^2} = 0 \Rightarrow 0 \le 2 \Rightarrow 0 \in B\\\\x = 1 \Rightarrow {(1)^2} = 1 \Rightarrow 1 \le 2 \Rightarrow 1 \in B\\\\x = 2 \Rightarrow {(2)^2} = 4 \Rightarrow 4 > 2 \Rightarrow 2 \notin B\\\\B = \{ x|x \in A,{\mkern 1mu} {\mkern 1mu} {x^2} \le 2\} = \{ - 1,0,1\} \end{array}\)
\(\begin{array}{l}C = \{ x|x \in A{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} - 1 \le x \le 1\} \\\\x = - 2 \Rightarrow - 2 < - 1 \Rightarrow - 2 \notin C\\\\x = - 1 \Rightarrow - 1 \le - 1 \le 1 \Rightarrow - 1 \in C\\\\x = 0 \Rightarrow - 1 \le 0 \le 1 \Rightarrow 0 \in C\\\\x = 1 \Rightarrow - 1 \le 1 \le 1 \Rightarrow 1 \in C\\\\x = 2 \Rightarrow 2 > 1 \Rightarrow 2 \notin C\\\\C = \{ x|x \in A{\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} - 1 \le x \le 1\} = \{ - 1,0,1\} \end{array}\)
\(\begin{array}{l}D = \left\{ {x|x \in A,{x^4} = 1} \right\}\\\\{x^4} = 1 \Rightarrow x = \pm \sqrt 1 \Rightarrow x = \pm 1\\\\ \Rightarrow D = \left\{ {x|x \in A,{x^4} = 1} \right\} = \{ - 1,1\} \end{array}\)
مجموعه های B و C با هم برابرند.
2 سه مجموعه مانند A، B و C بنویسید؛ به طوری که A⊆B و B⊆C آیا می توان نتیجه گرفت A⊆C؟
بله
A = {1} , B = {1, 2} , C = {1, 2, 3} ⇒ A⊆B⊆C
بنابراین داریم A⊆C است زیرا تمام اعضای مجموعه A در مجموعه B وچود دارد (A⊆B) و تمام اعضای مجموعه B در مجموعه C، موجود است (B⊆C) بنابراین تمام اعضای مجموعه A در مجموعه C موجود است لذا داریم A⊆C
3 تمام زیرمجموعه های هریک از مجموعه های زیر را بنویسید:
الف \(A = \left\{ {x|x \in \mathbb{N},2x + 1 = 3} \right\}\)
ب \(B = \left\{ {2x|x = 0,2,3} \right\}\)
الف
\(\begin{array}{l}A = \{ x|x \in \mathbb{N},\;2x + 1 = 3\} \\\\ \Rightarrow 2x + 1 = 3\\\\ \Rightarrow 2x = 2\\\\ \Rightarrow x = 1\\\\ \Rightarrow A = \{ 1\} \end{array}\)
بنابراین زیر مجموعه های مجموعه A بصورت زیر خواهد بود.
\(\emptyset ,{\rm{ }}\{ 1\} \)
ب
\(B = \left\{ {2x|x = 0,2,3} \right\} = \{ 0,4,6\} \)
بنابراین زیر مجموعه های مجموعه B بصورت زیر خواهد بود.
\(\begin{array}{l}\emptyset ,\{ 0\} ,\{ 4\} ,\{ 6\} ,\\\\\{ 0,4\} ,\{ 0,6\} ,\{ 4,6\} ,\\\\\{ 0,4,6\} \end{array}\)
4 نمودار روبه رو، وضعیت مجموعه های Q، W، N و Z را نسبت به هم نشان می دهد؛ آنها را نام گذاری و با علامت ⊆ باهم مقایسه کنید.
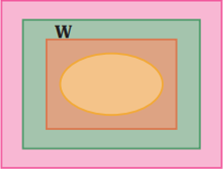
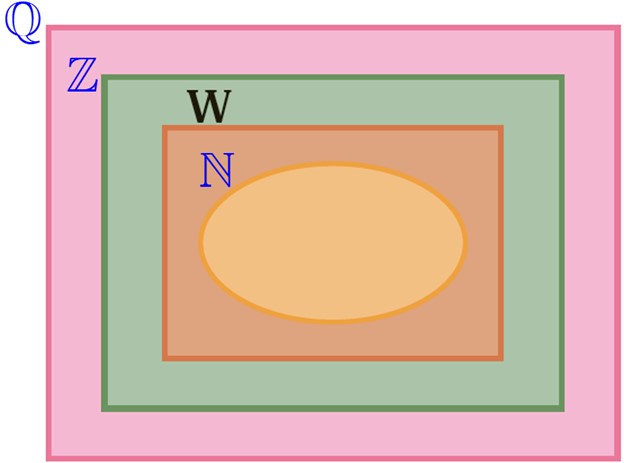
N⊆W⊆Z⊆Q
5 درستی یا نادرستی عبارت های زیر را با ذکر دلیل مشخص کنید:
الف هر عدد گویا عددی حسابی است.
ب هر عدد حسابی عددی گویاست.
ج هر عدد صحیح عددی گویاست.
د بعضی از عددهای گویا، عدد صحیح اند.
الف
نادرست
ب
درست
ج
درست
د
درست
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















