گام به گام کار در کلاس صفحه 8 درس مجموعه ها ریاضی نهم

1- با توجه به نمودار مقابل، دلیل درستی یا نادرستی عبارت های زیر را مشخص کنید:

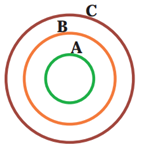
\(A \not\subset C\)  ,  \(B \subseteq A\)  ,  \(C \not\subset A\)  ,  \(\emptyset \subseteq A\)  ,  \(B \subseteq C\)  ,  \(A \subseteq B\)

2- مجموعه های B، A و C را درنظر بگیرید؛ سپس درستی یا نادرستی عبارت های زیر را مشخص کنید (با ذکر دلیل):

\(A = \left\{ {1,3,6,4} \right\}\)  ,  \(B = \left\{ {5,1,3} \right\} \)  ,  \(C = \left\{ {2,5,1,3,6} \right\}\)

\(B \not\subset A\),  \(3 \subseteq B\),  \(A \subseteq B\),  \(B \subseteq C\),  \(A \not\subset C\),  \(2 \in A\),  \(\left\{ {1,4} \right\} \in A\),  \(6 \notin A\),  \(\left\{ {5,6} \right\} \subseteq C\),  \(5 \in C \),  \(0 \subseteq A\)

3- همه زیر مجموعه های {a,b,c} = A در زیر نوشته شده است

∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}

مانند نمونه، تمام زیرمجموعه های هریک از مجموعه های زیر را بنویسید:

الف) مجموعه عددهای طبیعی بین ٩ و ١٢

ب) {a,b,c,d}

1-

\(A \not\subset C\) : (غلط) نمودار A داخل نمودار C است پس A زیر مجموعه C می باشد

\(B \subseteq A\)  : (غلط) مجموعه  B مجموعه ی B را در خودش دارد لذا B زیرمجموعه ی A نادرست است

\(C \not\subset A\)  :  (درست) مجموعه A داخل مجموعه C است پس مجموعه C زیرمجموعهA  نیست

\(\emptyset  \subseteq A\)  :  (درست) تهی عضوی ندارد و زیر مجموعه تمام مجموعه هاست

\(B \subseteq C\)  :   (درست) نمودار B داخل نمودار C است پس B زیرمجموعه C می باشد

\(A \subseteq B\)  :   (درست) نمودار A داخل نمودار B است پس A زیرمجموعه B می باشد

2-

\(B \not\subset A\) : (درست)   زیرا 5 عضو B ولی 5 عضو A نیست

\(3 \subseteq B\) : (غلط)    سمت چپ مجموعه نمیباشد

\(A \subseteq B\) : (غلط)   زیرا \(A \in A{\rm{ }}\) می باشد ولی \(A \notin B\)

\(B \subseteq C\) : (درست)    تمام اعضای B در مجموعه C موجود می باشد

\(A \not\subset C\) : (درست)   چون 4 عضو A هست اما عضو C نیست

\(2 \in A\) : (غلط)   عدد 2 در مجموعه A نیست

\(\left\{ {1,4} \right\} \in A\) : (غلط)   اعضای مجموعه ی سمت چپ در مجموعه ی A وجود دارد ولی مجموعه ی {1و4} عضو مجموعه A نیست

\(6 \notin A\) : (غلط)    عدد 6 عضو A می باشد

\(\left\{ {5,6} \right\} \subseteq C\) : (درست)    اعضای مجموعه سمت چپ در مجموعه C وجود ندارد

\(5 \in C\) : (درست)   عدد 5 عضو C می باشد

\(0 \subseteq A\) : (غلط)   سمت چپ مجموعه نیست

3- الف) تهی و {1} و {2} و {10 و 11}

ب) تهی و

{a} , {b} , {c} , {d} , {a, b} , {a, c} , {a, d} , {b, c} , {b, d} , {c, d} , {a, b, c} {a, b, d} , {a, c, d} , {b, c, d} , {a, b, c, d}