جواب تمرین صفحه 14 درس 1 ریاضی نهم (مجموعه ها)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 14 ریاضی نهم
-گام به گام تمرین صفحه 14 درس مجموعه ها
-تمرین صفحه 14 درس 1
-شما در حال مشاهده جواب تمرین صفحه 14 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 مجموعه های \(A = \left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\}\) و \(B = \left\{ {1\,,\,5\,,\,7\,,\,3\,,\,9} \right\}\) و \(C = \left\{ {1\,,\,7\,,\,10\,,\,11} \right\}\) را در نظر بگیرید؛ سپس هر یک از مجموعه های زیر را با عضوهایشان مشخص کنید:
\(A \cup B\) الف
\(B \cup C\) ب
\(A \cup C\) ج
\(A \cap B\) د
\(A - B\) هـ
\(C - B\) و
\((A - C) \cup (B - C)\) ز
\((A \cup B) - C\) ح
\(A \cap A\) ط
\(A \cap \emptyset \) ی
\(B \cup B\) ک
\(C \cup \emptyset \) ل
الف
\(\begin{array}{l}A \cup B = \left\{ {1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\,,\,7\,,\,8\,,\,9} \right\}\\\\ \Rightarrow n(A \cup B) = 9\end{array}\)
ب
\(\begin{array}{l}B \cup C = \left\{ {1\,,\,3\,,\,5\,,\,7\,,\,9\,,\,10\,,\,11} \right\}\\\\ \Rightarrow n(B \cup C) = 7\end{array}\)
ج
\(\begin{array}{l}A \cup C = \left\{ {1\,,\,2\,,\,4\,,\,6\,,\,7\,,\,8\,,\,9\,,\,10\,,\,11} \right\}\\\\ \Rightarrow n(A \cup C) = 9\end{array}\)
3
د
\(\begin{array}{l}A \cap B = \left\{ 9 \right\}\\\\ \Rightarrow n(A \cap B) = 1\end{array}\)
هـ
\(\begin{array}{l}A - B = \left\{ {2\,,\,4\,,\,6\,,\,8} \right\}\\\\ \Rightarrow n(A - B) = 4\end{array}\)
و
\(\begin{array}{l}C - B = \left\{ {10\,,\,11} \right\}\\\\ \Rightarrow n(C - B) = 2\end{array}\)
ز
\(\begin{array}{l}(A - C) \cup (B - C) = \\\\\left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\} \cup \left\{ {3\,,\,5\,,\,9} \right\} = \\\\\left\{ {2\,,\,3\,,\,4\,,\,5\,,\,6\,,\,8\,,\,9} \right\}\\\\ \Rightarrow n((A - C) \cup (B - C)) = 7\end{array}\)
ح
\(\begin{array}{l}(A \cup B) - C = \\\\\left\{ {1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\,,\,7\,,\,8\,,\,9} \right\} - \left\{ {1\,,\,7\,,\,10\,,\,11} \right\} = \\\\\left\{ {2\,,\,3\,,\,4\,,\,5\,,\,6\,,\,8\,,\,9} \right\}\\\\ \Rightarrow n((A \cup B) - C) = 7\end{array}\)
ط
\(\begin{array}{l}A \cap A = \\\\\left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\} \cap \left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\} = \\\\\left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\} = A\\\\ \Rightarrow n(A \cap A) = 5\end{array}\)
ی
\(\begin{array}{l}A \cap \emptyset = \\\\\left\{ {2\,,\,4\,,\,6\,,\,8\,,\,9} \right\} \cap \left\{ {} \right\} = \\\\\left\{ {} \right\} = \emptyset \\\\ \Rightarrow n(A \cap \emptyset ) = 0\end{array}\)
ک
\(\begin{array}{l}B \cup B = \\\\\left\{ {1\,,\,5\,,\,7\,,\,3\,,\,9} \right\} \cup \left\{ {1\,,\,5\,,\,7\,,\,3\,,\,9} \right\} = \\\\\left\{ {1\,,\,5\,,\,7\,,\,3\,,\,9} \right\} = B\\\\ \Rightarrow n(B \cup B) = 5\end{array}\)
ل
\(\begin{array}{l}C \cup \emptyset = \left\{ {1\,,\,7\,,\,10\,,\,11} \right\} \cup \emptyset = \\\\\left\{ {1\,,\,7\,,\,10\,,\,11} \right\} = C\\\\ \Rightarrow n(C \cup \emptyset ) = 4\end{array}\)
2 با توجه به نمودار زیر، عبارت های درست را با P و گزاره های نادرست را × مشخص کنید:
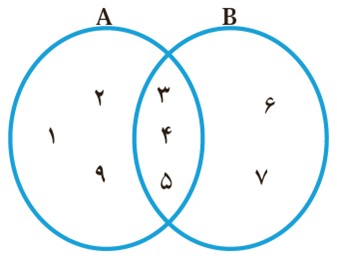
الف \(B - A = \left\{ {6\,,\,7} \right\}\)
ب \((A - B) \cup (A \cap B) = A\)
ج \((A - B) \cup (B - A) = \left\{ {1\,,\,2\,,\,6} \right\}\)
د \(n(A \cup B) = 8\)
هـ \(A - B = B - A\)
و \(n(A - B) = n(B - A)\)
الف
درست
ب
درست
\(\begin{array}{l}(A - B) \cup (A \cap B) = \\\\\left\{ {1\,\,,\,2\,,\,9} \right\} \cup \left\{ {3\,,\,4\,,\,5} \right\} = \\\\\left\{ {1\,\,,\,2\,,\,9\,,\,3\,,\,4\,,\,5} \right\} = A\end{array}\)
ج
نادرست
\(\begin{array}{l}(A - B) \cup (B - A) = \\\\\left\{ {1\,,\,2\,,\,9} \right\} \cup \left\{ {6\,,\,7} \right\} = \left\{ {1\,,\,2\,,\,9\,,\,6\,,\,7} \right\}\end{array}\)
د
درست
هـ
نادرست؛ در صورتی که \(A - B = B - A\) درست می باشد که \(A = B\) باشد.
و
نادرست
\(\begin{array}{l}n(A - B) = 3\\\\n(B - A) = 2\end{array}\)
3 کلمات و مجموعه های داده شدهٔ زیر را در جاهای خالی قرار دهید:
1 B
2 A
3 اجتماع
4 زیرمجموعۀ
5 \((A \cup B)\)
الف اشتراک دو مجموعه، زیر مجموعهٔ ______ همان دو مجموعه است.
ب هریک از دو مجموعهٔ A و B زیرمجموعهٔ ______ است.
ج اشتراک دو مجموعهٔ A و B ______ هر یک از دو مجموعهٔ A و B است.
د مجموعهٔ A-B زیرمجموعهٔ مجموعهٔ ______ است.
هـ اجتماع دو مجموعهٔ \((B - A)\) و \((A \cap B)\) با مجموعهٔ ______ مساوی است.
الف
اشتراک دو مجموعه، زیر مجموعهٔ اجتماع همان دو مجموعه است.
ب
هریک از دو مجموعهٔ A و B زیرمجموعهٔ \(A \cup B\) است.
ج
اشتراک دو مجموعهٔ A و B زیرمجموعۀ هر یک از دو مجموعهٔ A و B است.
د
مجموعهٔ A-B زیرمجموعهٔ مجموعهٔ A است.
هـ
اجتماع دو مجموعهٔ \((B - A)\) و \((A \cap B)\) با مجموعهٔ B مساوی است.
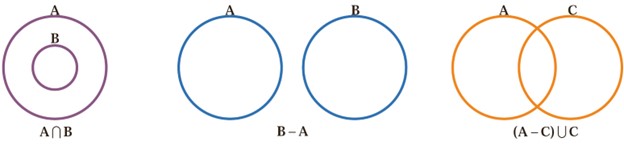
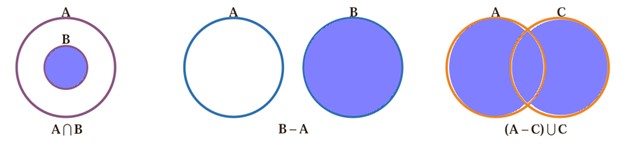
4 در هریک از شکل های زیر مجموعهٔ موردنظر را هاشور بزنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















