جواب فعالیت صفحه 31 درس 2 ریاضی دهم (مثلثات)
تعداد بازدید : 81.09Mپاسخ فعالیت صفحه 31 ریاضی دهم
-گام به گام فعالیت صفحه 31 درس مثلثات
-فعالیت صفحه 31 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 31 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در هر یک از شکل های زیر، جاهای خالی را کامل کنید.

\(\begin{array}{l}\tan A = \frac{{BC}}{{AB}} = \frac{5}{3}\;\;\;\;\;\;\;\;\;\cot M = \frac{{MN}}{{NO}} = \frac{{}}{{2/5}}\\\\\tan F = \frac{{\;\;\;\;}}{{}} = \frac{{\;\;\;\;}}{{}}\;\;\;\;\;\;\cot A = \frac{{\;\;\;\;}}{{}} = \frac{{\;\;\;\;}}{{}}\\\\\tan M = \frac{{\;\;\;\;}}{{}} = \frac{{\;\;\;\;}}{{}}\;\;\;\;\;\;\cot F = \frac{{\;\;\;\;}}{{}} = \frac{{\;\;\;\;}}{{}}\end{array}\)
\(\begin{array}{l}\tan A = \frac{{BC}}{{AB}} = \frac{5}{3}\;\;\;\;\;\cot M = \frac{{MN}}{{NO}} = \frac{2}{{2/5}}\\\\\tan F = \frac{{GF}}{{EF}} = \frac{4}{2}\;\;\;\;\;\;\cot A = \frac{{AB}}{{BC}} = \frac{3}{5}\\\\\tan M = \frac{{AB}}{{BC}} = \frac{3}{5}\;\;\;\;\;\cot F = \frac{{EF}}{{GF}} = \frac{2}{4}\end{array}\)
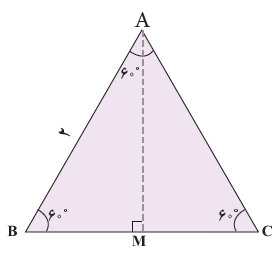
2 مثلث متساوی الاضلاع ABC با اضلاعی به طول 2 واحد را درنظر بگیرید.
الف محل برخورد نیمساز زاویهٔ A با پاره خط BC را M بنامید. با توجه به خواص مثلث متساوی الساقین، AM ........... ضلع BC است. بنابراین
BM = MC = …….
ب با استفاده از رابطهٔ فیثاغورس، طول AM و حاصل کسرهای زیر را به دست آورید.
\(\tan 30^\circ = \frac{{BM}}{{AM}} = \frac{{\;\;\;\;}}{{}}\;\;,\;\;\tan 60^\circ = \frac{{AM}}{{BM}} = \frac{{\;\;\;\;}}{{}}\)
پ با استفاده از یک مثلث قائم الزاویهٔ متساوی الساقین، تانژانت و کتانژانت زاویهٔ °45 را پیدا کنید.
الف محل برخورد نیمساز زاویهٔ A با پاره خط BC را M بنامید. با توجه به خواص مثلث متساوی الساقین، AM ...میانه... ضلع BC است. بنابراین
\(BM = MC = \frac{1}{2}AB = 1\)
ب
\(\begin{array}{*{20}{l}}{\tan 30^\circ = \frac{{BM}}{{AM}} = \frac{1}{{\sqrt 3 }}\:\:,\:}\\{}\\\begin{array}{l}\tan 60^\circ = \frac{{AM}}{{BM}} = \frac{{\sqrt 3 }}{1}{\mkern 1mu} .\\\\AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {{2^2} - 1} = \sqrt 3 \end{array}\end{array}\)
پ
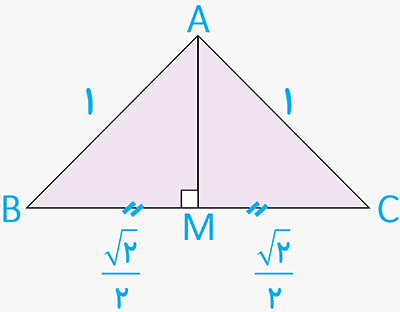
\(\begin{array}{l}AM = \sqrt {A{B^2} - BM{\,^2}} = \sqrt {{1^2} - {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} \\\\ = \sqrt {1 - \frac{1}{2}} = \frac{{\sqrt 2 }}{2}\\\\\tan \left( {{{45}^ \circ }} \right) = \frac{{AM}}{{BM}} = \frac{{\frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}} = 1\quad \quad \quad \\\\\cot \left( {{{45}^ \circ }} \right) = \frac{{BM}}{{AM}} = \frac{{\frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}} = 1\end{array}\)
در هر مثلث قائم الزاویه ABC، نسبت طول ضلع مقابل زاویهٔ حادهٔ A به طول وتر، همواره A می نامیم و با sinA نشان می دهیم. به عبارت دیگر
\(\sin A = \frac{{BC}}{{AC}}\)
همچنین نسبت طول ضلع مجاور زاویهٔ حادهٔ A به طول وتر نیز مقداری ثابت است که آن را کسینوس زاویهٔ A می نامیم و آن را با cosA نشان می دهیم. به عبارت دیگر \(\cos A = \frac{{\;\;\;\;}}{{}}\).
به سادگی می توان دید در مثلث قائم الزاویهٔ ABC ، \(\tan A = \frac{{BC}}{{AB}} = \frac{{\frac{{BC}}{{AC}}}}{{\frac{{AB}}{{AC}}}} = \frac{{\sin A}}{{\cos A}}\) و از این رو \(\tan A = \frac{{\sin A}}{{\cos A}}\) . به طور مشابه، می توان دید \(\cot A = \frac{{\cos A}}{{\sin A}}\)
همچنین نسبت طول ضلع مجاور زاویهٔ حادهٔ A به طول وتر نیز مقداری ثابت است که آن را کسینوس زاویهٔ A می نامیم و آن را با cosA نشان می دهیم. به عبارت دیگر \(\cos A = \frac{{AB}}{{AC}}\).
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















