جواب فعالیت صفحه 42 درس 2 ریاضی دهم (مثلثات)
تعداد بازدید : 81.09Mپاسخ فعالیت صفحه 42 ریاضی دهم
-گام به گام فعالیت صفحه 42 درس مثلثات
-فعالیت صفحه 42 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 42 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
مثلث قائم الزاویهٔ ABC را درنظر بگیرید.
الف اندازهٔ وتر یعنی x را بیابید و سپس مقدار عددی هر یک از چهار نسبت مثلثاتی را برای زاویۀ θ و α به دست آورید.
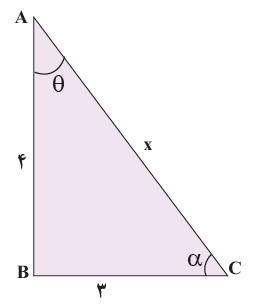
\(\begin{array}{l}\sin \theta = \frac{{BC}}{{AC}} = \frac{{\;3\,}}{{}}\\\\\sin \alpha = \,........\\\\\cos \theta = \,.......\\\\\cos \alpha = \frac{{BC}}{{AC}} = \frac{{\;3\,}}{{}}\\\\\tan \theta = \frac{{BC}}{{AB}} = \frac{{\sin \theta }}{{\cos \theta }} = .......\\\\\tan \alpha = \frac{{AB}}{{BC}} = .........\\\\\cot \theta = \frac{{\,\,1\,\,}}{{}} = \frac{{\cos \theta }}{{}} = ...........\\\\\cot \alpha = ...........\end{array}\)
ب با توجه به مقادیر عددی حاصل در قسمت (الف) مقدار \({\sin ^2}\theta + {\cos ^2}\theta \) و \({\sin ^2}\alpha + {\cos ^2}\alpha \) را به دست آورید.
پ درستی رابطۀ \({\sin ^2}\theta + {\cos ^2}\theta = 1\) را با استفاده از تعریف و اضلاع مثلث، بررسی کنید.
\({\left( {\sin \theta } \right)^2} + {\left( {\cos \theta } \right)^2} = {\sin ^2} + {\cos ^2}\theta = {\left( {\frac{{BC}}{{AC}}} \right)^2} + {\left( {\frac{{AB}}{{AC}}} \right)^2} = \frac{{B{C^2} + A{B^2}}}{{A{C^2}}} = ..........\)
پ مشابه قسمت (پ) درستی رابطهٔ \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) را بررسی کنید.
الف
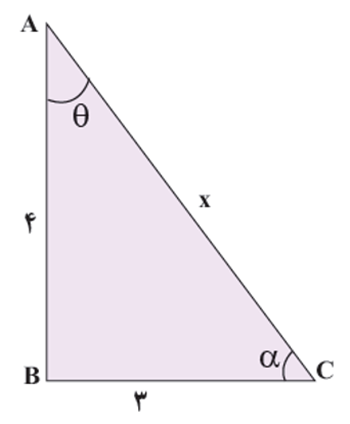
\(\begin{array}{l}x = \sqrt {{4^2} + {3^2}} = \sqrt {25} = 5\\\\\sin \theta = \frac{{BC}}{{AC}} = \frac{3}{5}\\\\\sin \alpha = \,\frac{4}{5}\\\\\cos \theta = \,\frac{4}{5}\\\\\cos \alpha = \frac{{BC}}{{AC}} = \frac{{\;3\,}}{5}\\\\\tan \theta = \frac{{BC}}{{AB}} = \frac{{\sin \theta }}{{\cos \theta }} = \frac{{\frac{3}{5}}}{{\frac{4}{5}}} = \frac{3}{4}\\\\\tan \alpha = \frac{{AB}}{{BC}} = \frac{{\frac{4}{5}}}{{\frac{3}{5}}} = \frac{4}{3}\\\\\cot \theta = \frac{1}{{\tan \theta }} = \frac{{\cos \theta }}{{\sin \theta }} = \frac{4}{3}.\\\\\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{3}{4}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{{{\sin }^2}\:\theta + {{\cos }^2}\:\theta = {{\left( {\frac{3}{5}} \right)}^2} + {{\left( {\frac{4}{5}} \right)}^2}}\\{ = \frac{9}{{25}} + \frac{{16}}{{25}} = \frac{{25}}{{25}} = 1}\\{}\\{{{\sin }^2}\:\alpha + {{\cos }^2}\:\alpha = {{\left( {\frac{4}{5}} \right)}^2} + {{\left( {\frac{3}{5}} \right)}^2}}\\{ = \frac{{16}}{{25}} + \frac{9}{{25}} = \frac{{25}}{{25}} = 1}\end{array}\)
پ
\(\begin{array}{l}{\left( {\sin \theta } \right)^2} + {\left( {\cos \theta } \right)^2} = {\sin ^2}\theta + {\cos ^2}\theta \\\\ = {\left( {\frac{{BC}}{{AC}}} \right)^2} + {\left( {\frac{{AB}}{{AC}}} \right)^2} = \frac{{B{C^2} + A{B^2}}}{{A{C^2}}}\\\\ = \frac{{A{C^2}}}{{A{C^2}}} = 1\end{array}\)
ت
\(\begin{array}{l}{\left( {\sin \:\alpha } \right)^2} + {\left( {\cos \:\alpha } \right)^2} = {\sin ^2}\:\alpha + {\cos ^2}\:\alpha \\\\ = {\left( {\frac{{AB}}{{AC}}} \right)^2} + {\left( {\frac{{BC}}{{AC}}} \right)^2}\\\\ = \frac{{A{B^2} + B{C^2}}}{{A{C^2}}} = \frac{{A{C^2}}}{{A{C^2}}} = 1\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















