درسنامه کامل ریاضی هفتم فصل 1 راهبردهای حل مسئله
تعداد بازدید : 3.73Mخلاصه نکات ریاضی هفتم فصل 1 راهبردهای حل مسئله - درسنامه شب امتحان ریاضی هفتم فصل 1 راهبردهای حل مسئله - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 1 راهبردهای حل مسئله
راهبردهای حل مسئله
مراحل حل یک مسئله
برای حل یک مسئله بایستی دو روش زیر را به کار ببریم:
1) فهمیدن مسئله
2) انتخاب راهبرد مناسب
1- فهمیدن مسئله
یعنی ارتباطی بین اطلاعات داده شده در مسئله و خواسته های آن پیدا کرده و آن ها را به خوبی درک کنیم. برای فهمیدن یک مسئله می توانیم کارهایی که در زیر آمده است را دنبال کنیم:
1) اطلاعات داده شده در مسئله را مشخص کنیم.
2) خواسته های مسئله را نیز مشخص کنیم.
3) مسئله را به صورت خلاصه شده بیان کنیم.
4) مسئله را با زبان و بیان خود توضیح دهیم.
5) مسئله را نمایش دهیم.
6) از شکل ها و اشیا برای مدل سازی در حل مسئله استفاده کنیم.
2- انتخاب راهبرد مناسب
انتخاب راهبرد مناسب یعنی یک روش یا راه حل مناسب برای حل مسئله یافته و با مرور راهبردها، تشخیص دهیم که کدام یک برای حل مسئله مناسب می باشد.
راهبردهای حل مسئله
1- راهبرد رسم شکل
۲- راهبرد الگوسازی (تفکّر نظام دار)
3- راهبرد حذف حالت های نامطلوب
4- راهبرد الگویابی
5- راهبرد حدس و آزمایش
6- راهبرد زیر مسئله
۷- راهبرد حل مسئله ساده تر
۸- راهبرد روش های نمادین
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
راهبرد الگوسازی (تفکّر نظام دار)
راهبرد الگوسازی
برای حل بعضی از مسئله ها باید همه حالت های ممکن را بنویسید. برای اینکه هیچ حالتی از قلم نیفتد، لازم است آنها را با نظم، الگو و ترتیبی مشخص بنویسید. الگوسازی به شما کمک می کند تا مطمئن شوید همه حالت ها را نوشته اید. بنابراین در مسئله هایی که لازم است همه جواب ها و پاسخ های ممکن را بنویسید، می توانید از این راهبرد استفاده کنید. با توجه به نظم و ترتیبی که می سازید به این راهبرد تفکر نظام دار نیز می گویند.
دو عدد طبیعی پیدا کنید که حاصل ضرب آنها ۲۴ و حاصل جمع آنها کمترین مقدار باشد. جدول را با یک نظم و ترتیب کامل کنید.
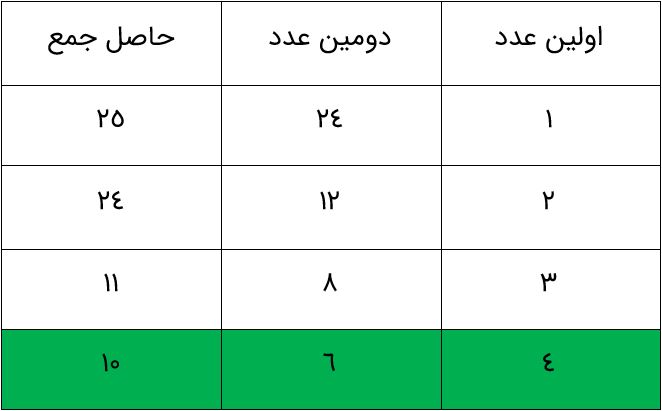
جواب سطر رنگی می باشد.
مجموع دو عدد طبیعی 24 است. حداکثر حاصل ضرب آن ها کدام است؟
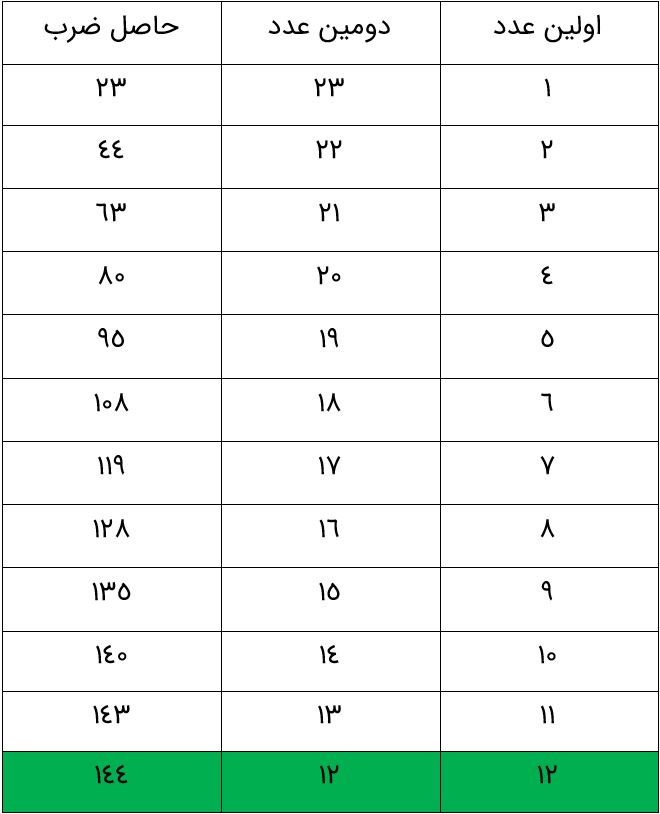
بیشترین مقدار حاصل ضرب عدد 144 می باشد.
با رقم های 6، 7 و 9 چند عدد دو رقمی بدون تکرار رقم های می توان نوشت؟
باید سعی کنیم همه حالت های ممکن را بیابیم:
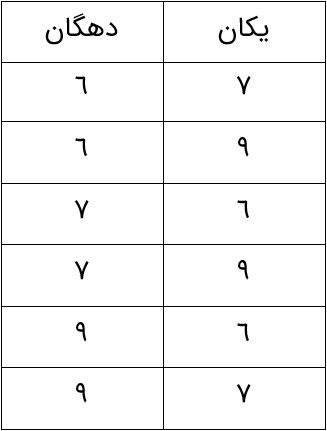
6 عدد دو رقمی بدون تکرار رقم ها می توان نوشت. دقت کنید که ابتدا دهگان را ثابت گرفتبم و حالت ها را نوشتیم.
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
راهبرد حذف حالت های نامطلوب
راهبرد حذف حالت های نامطلوب
به شرایط و اطّلاعات مسئله توجه کنید و حالت های نامطلوب و نادرست را کنار بگذارید. آنگاه پاسخ مسئله یا همان حالت های مطلوب به دست می آیند. برای پیدا کردن تمام حالت های ممکن می توانید از راهبرد الگوسازی استفاده کنید . ابتدا فهرستی از تمام حالت ها به دست آورید؛ سپس با توجه به شرایط گفته شده در مسئله، حالت های نامطلوب را حذف کنید.
مجموع سن سه نفر ۱۴ سال و حاصل ضرب سن آنها ۷۰ است. سن بزرگ ترین نفر چقدر است؟
سن بزرگ ترین نفر 7 سال می باشد.
مجموع ۳ عدد متفاوت ۱۱ و حاصل ضرب آنها ۳۶ شده است. این اعداد را مشخص کنید.
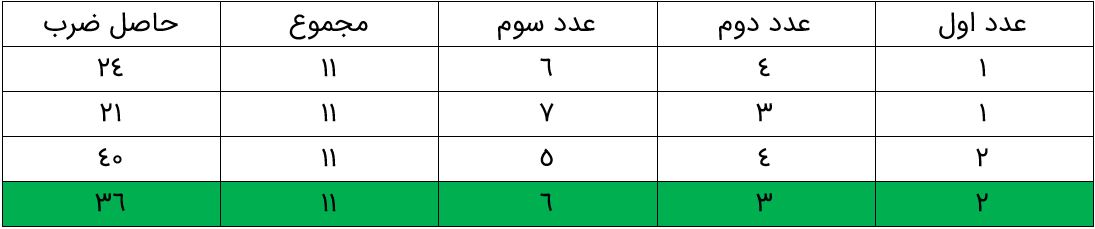
این اعداد به ترتیب 2، 3 و 6 می باشند.
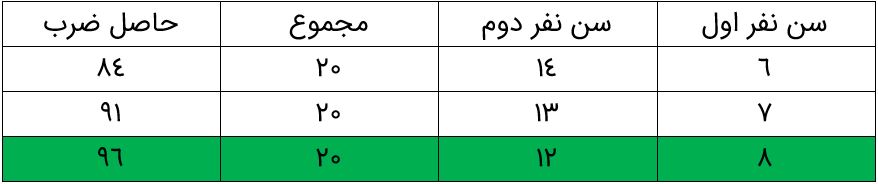
مجموع سن دو نفر ۲۰ سال و حاصل ضرب سن آنها ۹۶ است. اختلاف سن آنها را بیابید.
راهبرد الگویابی
راهبرد الگویابی
در ریاضی با دو نوع الگوی عددی یا هندسی رو به رو می شویم. کشف الگو، رابطه و نظم موجود در بین دنباله های عددی یا هندسی کمک می کند تا بتوانید خواسته مسئله را به دست آورید. این راهبرد در مسئله هایی کاربرد دارد که بین شکل ها یا عددها، الگو و رابطه خاصی وجود داشته باشد.
سه عدد بعدی الگوی زیر را بنویسید رابطه بین عددها را توضیح دهید.
\(1\;,\;4\;,\;9\;,\;16\;,\;\;\;,\;\;\;,\;\)
جواب:
اگر با دقت به اعداد این الگو توجه کنیم متوجه می شویم که همگی آنها مجذور شده اند ( به توان ۲ رسیده اند). پس مجذورهای بعدی را به سادگی می نویسیم:
\(1\;,\;4\;,\;9\;,\;16\;,\;25\;,\;36\;,\;49\)
به شکل زیر نگاه کنید. شکل دهم چند دایره خواهد داشت؟
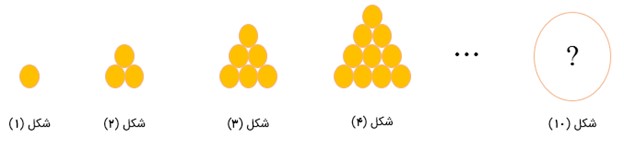
1 : شکل (1)
3 = 2 + 1 : شکل (2)
6 = 3 + 2 + 1 : شکل (3)
10 = 4 + 3 + 2 + 1 : شکل (4)
55 = 10 + 9 + ... + 4 + 3 + 2 + 1 : شکل (10)
حاصل عبارت زیر را بدست آورید.
\(\frac{{12}}{{13}} \times \frac{{13}}{{14}} \times \frac{{14}}{{15}} \times \cdots \times \frac{{112}}{{113}} = \)
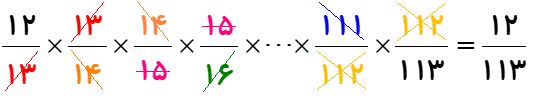
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
راهبرد حدس و آزمایش
راهبرد حدس و آزمایش
ممکن است حلّ یک مسئله، روش و راه حل مستقیمی نداشته باشد یا راه رسیدن به جواب آن طولانی و دشوار باشد. شما می توانید با یک روش منطقی و منظم پاسخ احتمالی مسئله را حدس بزنید؛ سپس با توجه به شرایط گفته شده در مسئله، حدس خود را بررسی کنید و با توجه به نتیجه به دست آمده حدس بعدی را بزنید تا کم کم به پاسخ مسئله نزدیک شوید. برای نشان دادن حدس ها و آزمایش های خود راه حل مناسبی پیدا کنید.
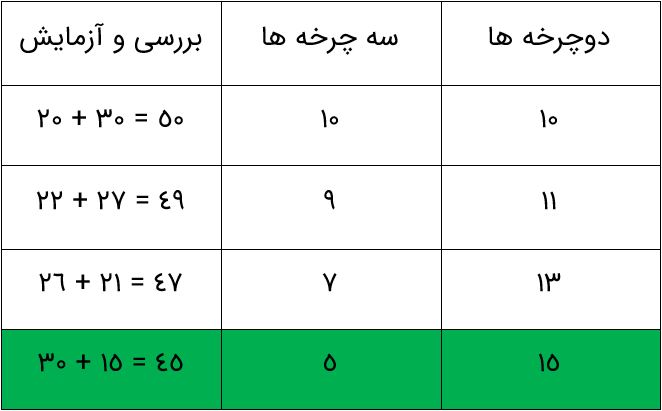
۲۰ دستگاه دوچرخه و سه چرخه در یک پارکینگ وجود دارد. اگر تعداد کل چرخ های آنها ۴۵ عدد باشد، چند دوچرخه و چند سه چرخه در پارکینگ وجود دارد؟
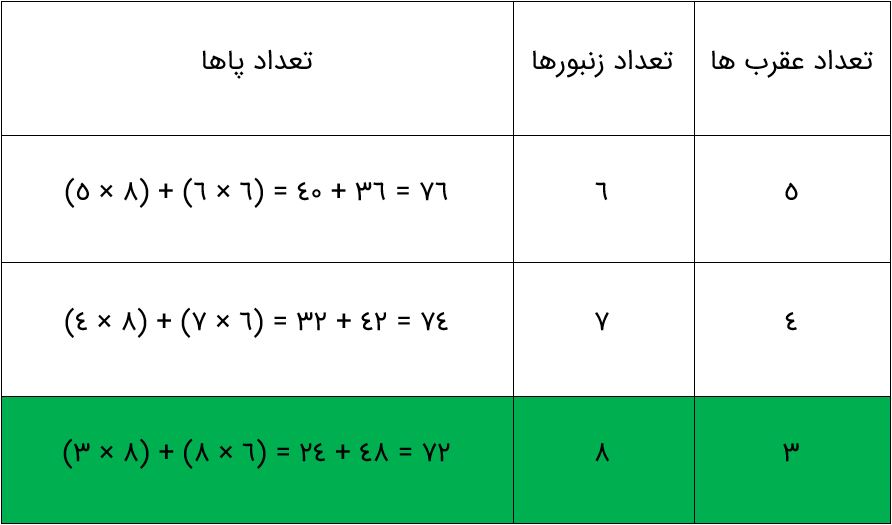
در یک ظرف شیشه ای تعدادی زنبور و عقرب انداخته ایم. اگر تعداد سرها 11 تا و مجموع پاهای آن ها 72 باشد، چند زنبور و چند عقرب در ظرف وجود دارد؟ (راهنمایی: عقرب ها 8 پا و زنبورها 6 پا دارند)
در جای خالی، عدد مناسب قرار دهید:
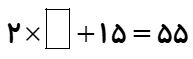\(% MathType!Translator!2!1!AMS LaTeX.tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbjjvqon % vyUnharmWu51MyVXgaruavP1wzZbItLDhis9wBH5gatCvAUfKCHjwA % Jbqegieil92BKf2Aaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaG % qiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0x % bba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adba % qaaeGaciGaaiaadeabauaadaGbaaGcbaGaeGOmaiJaey41aq7aauIh % aeaaaaGaey4kaSIaeGymaeJaeGynauJaeyypa0JaeGynauJaeGynau % daaa!483B! \[2 \times \boxed{} + 15 = 55\]% MathType!End!2!1! \)
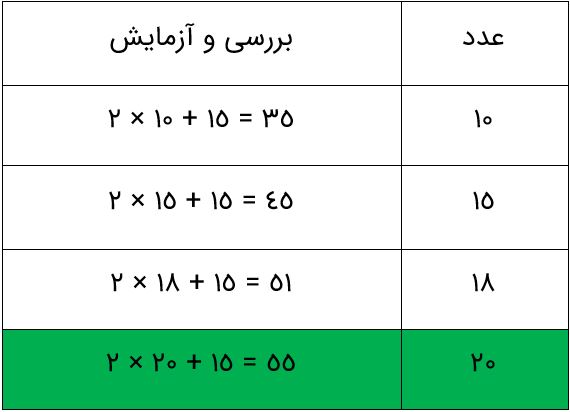
عدد مناسب جای خالی، 20 می باشد.
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
راهبرد زیر مسئله
راهبرد زیرمسئله
مسئله پیچیده و چند مرحله ای را به چند مسئله ساده تبدیل کنید. فهرستی از این زیر مسئله ها را درست کنید؛ سپس به ترتیب به آنها پاسخ دهید. اگر ترتیب زیر مسئله ها را درست تشخیص داده باشید، حل هر زیر مسئله به حل مسئله بعدی کمک می کند تا در نهایت به خواسته اصلی مسئله برسید.
پس انداز هفتگی محمد ۳۰۰۰ تومان است. او حساب کرد ۵ هفته پس انداز او نصف قیمت کیفی است که دوست دارد بخرد.
الف) پس انداز ۵ هفته چقدر می شود؟
ب) اگر این عدد نصف قیمت کیف باشد قیمت کیف چقدر است؟
الف)
\(3000\; \times \;5 = 15000\)
ب)
\(15000\; \times \;2 = 30000\)
خمس نصف عددی 5 است. دو برابر این عدد چند است؟
به فرض مسئله توجه کنید:
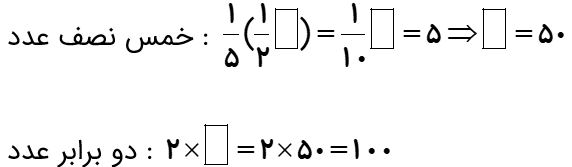
فروشنده ای به ازای هر کیلوگرم سیب 30% و به ازای هر کیلوگرم خیار 20% سود می کند. اگر این فروشنده 15 کیلوگرم سیب 5000 تومانی و 20 کیلوگرم خیار 4000 تومانی بفروشد، در مجموع چند تومان سود کرده است؟
تومان \(\frac{{30}}{{100}} \times 5000 \times 15 = 22500\) :سود حاصل از فروش سیب ها
تومان \(\frac{{20}}{{100}} \times 4000 \times 20 = 16000\) :سود حاصل از فروش خیار ها
تومان \(22500 + 16000 = 38500\) :سود کل <=
راهبرد حل مسئله ساده تر
راهبرد حل مسئله ساده تر
برای حل بعضی از مسئله ها، ابتدا مسئله ای ساده تر را که با مسئله اصلی در ارتباط است، حل می کنیم. سپس با استفاده از نتیجه و پاسخ مسئله ساده شده، جواب مسئله اصلی را به دست می آوریم. برای ساده کردن مسئله می توان از عددهای تقریبی یا عددهای کوچک تر استفاده کرد. برای نتیجه گیری و پیدا کردن پاسخ مسئله اصلی، از راهبرد الگویابی استفاده می کنیم و الگوی کشف شده در مسئله ساده را به مسئله اصلی مرتبط می کنیم.
قطر خورشید ۱۳۹۲۵۳۰ کیلومتر و قطر کره زمین 12756/6 کیلومتر است. قطر خورشید تقریباً چند برابر قطر زمین است؟
برای ساده شدن مسئله بهتر است از عددهای تقریبی استفاده کنید. خلاصه مسئله ساده شده را بنویسید و پاسخ دهید:
\(\begin{array}{l}1,392,530 \simeq 1,000,000\\\\12,756/6 \simeq 10,000\\\\1,000,000 \div 10,000 = 100\\\\1392530 \div 12,756/6 \simeq 100\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
راهبرد روش های نمادین
راهبرد روش های نمادین
بسیاری از مسئله ها را می توانیم به کمک نمادهای جبری به یک معادله تبدیل کنیم. از فصل سوم به بعد می توانید از این راهبرد نیز برای حل مسئله استفاده کنید. در بعضی از مسئله ها هم می توانیم از مدل سازی هندسی استفاده کنیم. تبدیل مسئله به یک شکل هندسی و حل هندسی آن نیز نوعی روش نمادین یا مدل سازی به شمار می رود.
احمد ۳۰۰۰۰ تومان پول داشت. او ۴ دفتر خرید و ۲۰۰۰ تومان برایش باقی ماند. قیمت هر دفتر چقدر است؟
متن این سؤال را می توانید با تساوی زیر نشان دهید:
که مربع نشان دهنده تعداد دفترهاست.
اکنون می توانید عددی را که باید در مربع قرار گیرد حدس بزنید و آزمایش کنید.
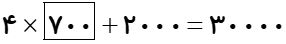
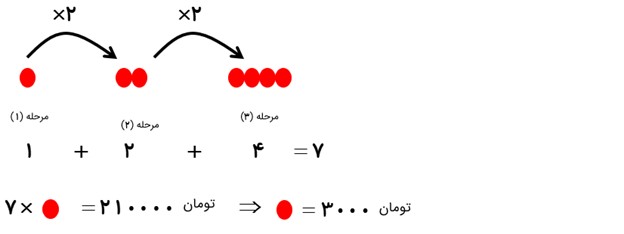
در یک کاری، جریمه عقب افتادگی کار دو برابر جریمه عقب افتادگی قبلی است. اگر یک کارگر پس از 3 بار عقب افتادگی در مجموع 210000 تومان جریمه شود، جریمه عقب افتادگی اول او چقدر بوده است؟
در این سوال هر جریمه عقب افتادگی دو برابر جریمه عقب افتادگی قبلی است:
ثلث پول حسین با چهار برابر پول رضا برابر است. اگر آنها در مجموع 26000 تومان پول داشته باشند، پول حسین چند تومان است؟
با دو مجهول سر و کار داریم. با استفاده از نمادهای زیر، مسئله را حل می نماییم:
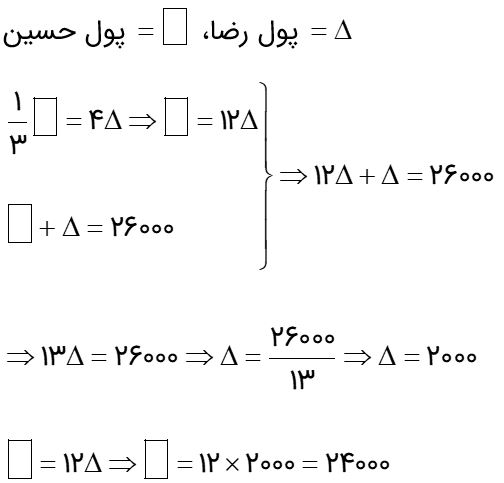
تومان 2000 = پول رضا، تومان 24000 = پول حسین
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
راهبرد رسم شکل
راهبرد رسم شکل
کشیدن یک شکل مناسب می تواند به حل مسئله کمک کند یا به طور کامل آن را حل کند؛ به طوری که نیازی به نوشتن عملیات و محاسبه نباشد. گاهی ممکن است شکل را فقط تصور کنید و آن را رسم نکنید. منظور از رسم شکل، نقاشی نیست، بلکه می توانید برای این کار شکل های ساده بکشید.
مثال
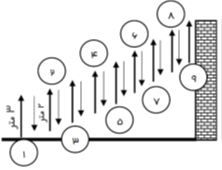
قورباغه ای می خواهد از یک دیوار عمودی بالا برود. او با هر جهش ۳ متر بالا می رود و هر بار ۲ سر می خورد و پایین می آید. اگر ارتفاع دیوار ۹ متر باشد ، او با چند جهش به بالای دیوار می رسد؟
همانطور که در شکل پیداست با نهمین پرش به بالای دیوار می رسد.
مثال
توپی از ارتفاع 32 متری سطح زمین رها می شود و پس از هر بار برخورد با زمین نصف ارتفاع قبلی خود را بالا می آید. این توپ از لحظه رها شدن تا سومین مرتبه که به زمین می خورد، چند متر حرکت کرده است؟
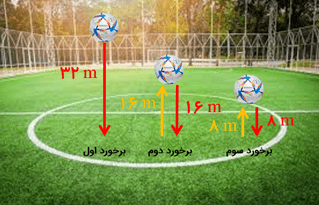
\(32 + 16 + 16 + 8 + 8 = 80\,m\)
یک استخر مستطیل شکلی به طول 6 متر و عرض 4 متر در باغچه ای وجود دارد. می خواهیم به فاصله یک متر از لبه های استخر را دور تا دور آن حفاظ بکشیم. به چند متر از این حفاظ نیاز داریم؟
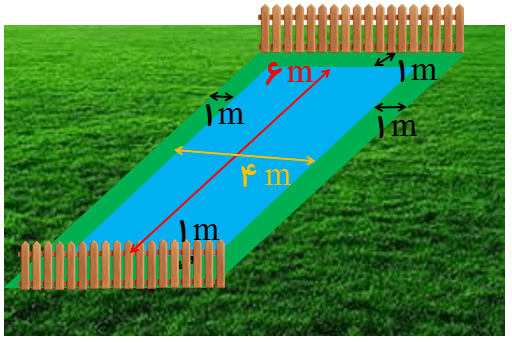
دور تا دور (محیط مستطیل)
2 × (عرض + مستطیل) = محیط مستطیل
8 = 2 + 6 = طول مستطیل
6 = 2 + 4 = عرض مستطیل
متر 28 = 2 × (6 + 8)