درسنامه کامل ریاضی هفتم فصل 6 سطح و حجم
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هفتم فصل 6 سطح و حجم - درسنامه شب امتحان ریاضی هفتم فصل 6 سطح و حجم - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 6 سطح و حجم
حجم و انواع آن
حجم
مقدار جایی که هر جسم در فضا اشغال می کند.
انواع حجم:
حجم ها را می توان به دو دسته هندسی و غیرهندسی تقسیم کرد. حجم های هندسی شکل های مشخص و تعریف دارند. حجم های هندسی را می توان به سه دسته تقسیم کرد:
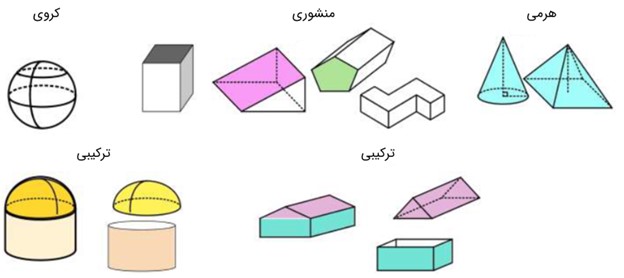
1) منشوری
2) کروی
3) هرمی
برخی از حجم های هندسی نیز ترکیبی از این سه نوع اند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
آشنایی بیشتر با حجم های منشوری
آشنایی بیشتر با حجم های منشوری
حجم های منشوری بین دو صفحه موازی قرار می گیرند. به این دو سطح موازی که سطح منشوری را قطع می کنند، «قاعده» و به سطح های اطراف آن «وجه های جانبی» می گویند.
به محل برخورد سطح ها، «یال» و به نقطه برخورد هر سه سطح «رأس» می گویند.
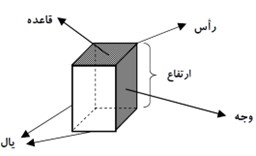
قاعده:
دو سطح بالا و پایین منشور.
وجه یا پهلو:
سطح های اطراف منشور.
یال:
محل برخورد هر دو وجه.
رأس:
محل برخورد یال ها.
ارتفاع:
فاصلۀ بین دو قاعده.
تعداد وجه ها یا پهلوها در حجم های منشوری:
۲ + تعداد ضلع های قاعده = تعداد وجه ها
تعداد یال ها در حجم های منشوری:
۳ × تعداد ضلع های قاعده = تعداد یال ها
تعداد رأس ها در حجم های منشوری:
2 × تعداد ضلع های قاعده = تعداد رأس ها
مقطع زدن:
برش زدن حجم های منشوری از ارتفاع آنها.
مثال
تعداد یال های یک مکعب مستطیل چند تا از تعداد رأس های آن بیشتر است؟
هر مکعب که مکعب مستطیل هم جزو آن دسته به شمار می آید، دارای 6 وجه، 12 یال، 8 رأس و 4 وجه جانبی است. بنابراین تعداد یال ها از تعداد رأس ها 4 عدد بیشتر است.
با 2000 مکعب کوچک، بزرگترین مکعب ممکن را ساخته ایم. چند مکعب کوچک اضافه آمده اند؟
بزرگ ترین مکعب ممکن را به کمک حدس و آزمایش بدست می آوریم:
\(\begin{array}{l}{10^3} = 1000\\{11^3} = 1331\\{12^3} = 1728\\{13^3} = 2197\end{array}\)
پس بزرگ ترین مکعب از 1728 مکعب کوچک ساخته می شود. بنابراین:
272 = 1728 – 2000 = تعداد اضافه مانده معکب های کوچک
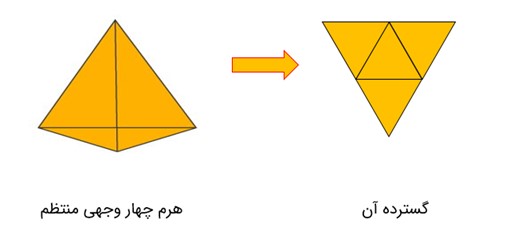
گسترده یک هرم چهار وجهی منتظم به چه صورت است؟
هرم چهار وجهی منتظم نوعی هرم است که از وجه های مثلث متساوی الاضلاع تشکیل شده است. بنابراین گسترده آن در شکل زیر آمده است:
تعداد وجه ها، رأس ها و یال های یک منشور که قاعده 5 ضلعی منتظم دارد را بدست آورید.
یک منشور که قاعده 5 ضلعی منتظم دارد در شکل زیر آمده است:
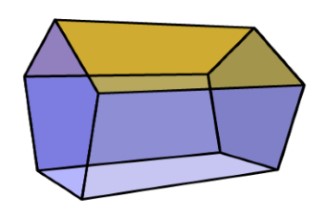
7 = 2 + 5= 2 + تعداد ضلع های قاعده = تعداد وجه ها
15 = 3 × 5 = 3 × تعداد ضلع های قاعده = تعداد یال ها
10 = 2 × 5 = 2 × تعداد ضلع های قاعده = تعداد رأس ها
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
جهت های دیدن یک حجم
یک حجم را می توان از چهار جهت بالا، روبرو، راست و پایین مشاهده و آن را روی کاغذ شطرنجی رسم کرد؛ مانند:
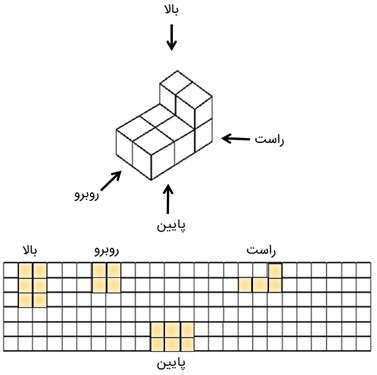
مثال
با توجه به زاویه دید شکل مقابل، حجم مقابل به چه شکلی دیده می شود؟
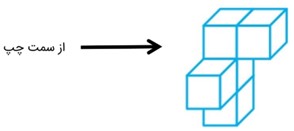
به صورت زیر دیده می شود:
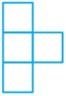
محاسبه حجم منشورها
تمام حجم های منشورها را می توانید از دستور زیر محاسبه کنید:
ارتفاع × مساحت قاعده = حجم منشور
رابطه جبری آن:
V = s.h
استوانه هم از حجم های منشوری حساب می شود که دارای قاعده دایره شکل می باشد.
واحدهای اندازه گیری حجم عبارتند از سانتیمتر مکعب و یا مترمکعب.
مثال
درون استوانه ای به شعاع 15 و ارتفاع 12، سوراخی به شعاع 5 ایجاد می کنیم. حجم شکل حاصل را بیابید.
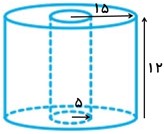
\( = \pi \times {15^2} \times 12 = 2700\pi \) حجم کل
\( = \pi \times {5^2} \times 12 = 300\pi \) حجم سوراخ
\( = 2700\pi - 300\pi = 2400\pi \) حجم شکل حاصل
درون مستطیلی به ابعاد 10 و 7 و ارتفاع 12، یک حفره استوانه ای شکل به شعاع قاعده 2 ایجاد می کنیم. اگر 3 = π ، حجم شکل حاصل را بیابید.
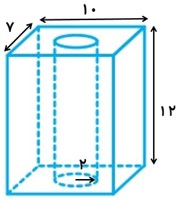
\( = 7 \times 10 \times 12 = 840\) حجم کل
\( = \pi \times {2^2} \times 12 = 48\pi = 48 \times 3 = 144\) حجم حفره
\( = 840 - 144 = 696\) حجم شکل حاصل
اگر شکل زیر را از قسمت نقطه چین تا بزنیم، یک جعبه به شکل مکعب مستطیل بدست می آید. حجم جعبه را بیابید.
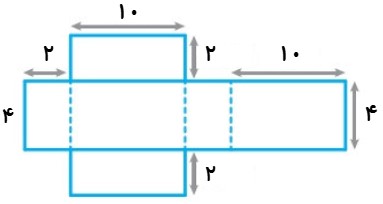
اگر به شکل دقت کنید، متوجه می شوید که:
2 = ارتفاع ، 4 = عرض ، 10 = طول
\( = 10 \times 4 \times 2 = 80\) حجم
اگر به ابعاد طول، عرض و ارتفاع مکعبی 20% اضافه کنیم، به حجم آن چند درصد اضافه می شود؟
اگر ابعاد مکعب را a در نظر بگیریم، داریم:
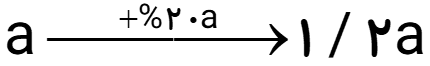
\( = 1/2 \times 1/2 \times 1/2 = 1/728\) حجم
\( \Rightarrow 1/728 - 1 = 0/728 = \% 72/8\)
به حجم مکعب 8/72 درصد اضافه می شود.
حجم شکل مقابل را به دست آورید. (3 = π)
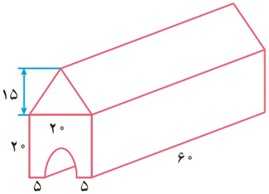
ارتفاع × مساحت قاعده = حجم
مساحت نیم دایره – مساحت مربع + مساحت مثلث = مساحت قاعده
\( = \frac{{20 \times 15}}{2} = 150\) مساحت مثلث
\( = 20 \times 20 = 400\) مساحت مربع
\( = \frac{{\pi \times {5^2}}}{2} = 12/5\pi = 12/5 \times 3 = 37/5\) مساحت نیم دایره
\( = \frac{{\pi \times {5^2}}}{2} = 150 + 400 - 37/5 = 512/5\) مساحت قاعده
\( = 512/5 \times 60 = 30750\) حجم
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
مساحت های جانبی و کل
مساحت جانبی
به مجموع مساحت همه وجه های جانبی منشور مساحت جانبی آن می گویند. برای یافتن مساحت جانبی تمام منشورها می توانید از دستور زیر آن را محاسبه نمایید:
ارتفاع × محیط قاعده = مساحت جانبی
رابطه جبری آن:
S = P.h
قبل از رسیدن به مساحت کل درباره گسترده یا همان پهن شده حجم های منشوری شناخت بیشتری بیابیم. در زیر گسترده بعضی از این احجام را ملاحظه می نمایید:
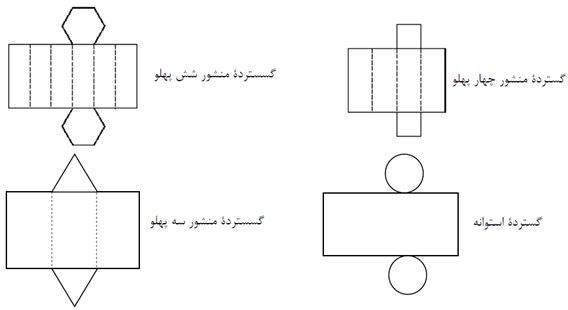
مساحت کل
به مجموع مساحت جانبی و مساحت دو قاعده تمامی منشورها، مساحت کل آن می گویند. برای یافتن مساحت کل تمام منشورها می توانید از دستور زیر آن را محاسبه نمایید:
مساحت دو قاعده + مساحت جانبی = مساحت کل
رابطه جبری آن:
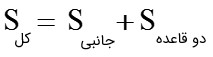
مثال
حجم یک مکعب \(27{a^3}\) است. مساحت جانبی آن کدام است؟
اگر x را ضلع مکعب در نظر بگیریم داریم:
\(27{a^3} = {x^3} \Rightarrow {3^3} \times {a^3} = {x^3} \Rightarrow {\left( {3a} \right)^3} = {x^3} \Rightarrow x = 3a\)
\( = 4{x^2} = 4{(3a)^2} = 4 \times 9{a^2} = 36{a^2}\) مساحت جانبی مکعب
نسبت حجم به مساحت کل یک مکعب به ضلع a را بیابید.
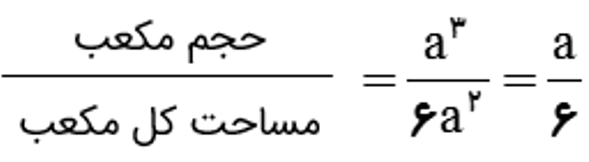
حجم و مساحت کل منشور روبرو را بدست آورید.
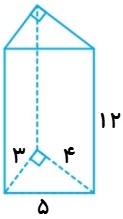
\( = (\frac{{3 \times 4}}{2}) \times 12 = 6 \times 12 = 72\) ارتفاع × مساحت قاعده = حجم
(مساحت قاعده × 2) + (ارتفاع × محیط قاعده) = مساحت کل
\(\begin{array}{l} = \left( {(3 + 4 + 5) \times 12} \right) + \left( {2 \times (\frac{{3 \times 4}}{2})} \right)\\ = 144 + 12 = 156\end{array}\)
اگر حجم یک مکعب، ربع مساحت کل آن باشد، مساحت جانبی آن چقدر است؟
ضلع مکعب را x فرض می کنیم؛ داریم:
\({x^3} = \frac{1}{4} \times 6{x^2} \Rightarrow x = \frac{6}{4} = \frac{3}{2}\)
\( = 4{x^2} = 4 \times \frac{3}{2} \times \frac{3}{2} = 9\) مساحت جانبی
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
حجم و سطح
یک مستطیل با طول و عرض مشخص را به دو صورت زیر لوله می کنیم تا استوانه به دست آید.
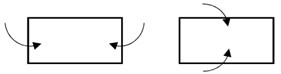
در هر حالت حجم استوانه ها را که به دست آوریم، مشاهده می کنیم این دو حجم با هم متفاوتند و این در حالی است که هر دو حجم از مستطیلی یک اندازه حاصل شده اند.
پس می توان نتیجه گرفت با حرکت یک سطح در فضا حجم ساخته می شود که احجام حاصل با هم متفاوتند. از این خاصیت در خراطی، تراشکاری و سفالگری برای ساختن حجم های مختلف استفاده می کنند.



1736019749.png)















