آیا درسنامه ریاضی هفتم فصل 3 جبر و معادله، مطابق با آخرین تغییرات کتب درسی است ؟

بله، درسنامه ریاضی هفتم فصل 3 مطابق با آخرین تغییرات کتب درسی 1402 - 1401 تدوین شده است.

آیا نکات درس به صورت کامل بیان شده اند ؟

بله، تمام نکات به صورت کاملا شیوا و با هدف یادگیری و تسلط به مبحث بیان شده اند.

درسنامه کامل ریاضی هفتم فصل 3 جبر و معادله

تعداد بازدید : 3.73M

خلاصه نکات ریاضی هفتم فصل 3 جبر و معادله - درسنامه شب امتحان ریاضی هفتم فصل 3 جبر و معادله - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 3 جبر و معادله

الگو

به رابطه ای منظم بین تعداد بی شمار عدد یا شکل گفته می شود؛ به منظور درک بهتر الگوها، آنها را به گروه های زیر طبقه بندی کرده ایم:

۱- الگوهای عددی و جمله n ام

در این الگوها با توجه به رابطه ای که بین اعداد وجود دارد، می توان به جمله n ام رسید.

مثال

جمله n ام الگوی عددی زیر را نوشته و جمله بیستم آن را حساب کنید.

\(1\,,\,3\,,\,5\,,\,...\)

ملاحظه می شود تفاوت هر جمله با جمله قبلش ۲ می باشد، پس عدد ۲ در تمامی جمله ها ضرب شده که یک واحد از آنها کم شده است. یعنی جمله ام این الگو می شود: \(2\,n - 1\)

\(2(20)\, - \,1 = 40\, - \,1 = 39\) :جمله بیستم

جمله n ام الگوی عددی زیر را بیابید.

\(1\,,\,5\,,\,9\,,\,13\,,\,...\)

ملاحظه می شود تفاوت هر جمله با جمله قبلش 4 می باشد، پس عدد 4 در تمامی جمله ها ضرب شده و مقدار ثابتی از این حاصل ضرب کم شده است که با کمی کنکاش، مقدار ثابت عدد 3- بدست می آید؛ چرا که وقتی جمله اول را بخواهیم بدست آوریم عدد 1 را در 4 ضرب کرده که حاصل ضرب عدد 4 می شود. حال بایستی با چه عددی جمع شود تا حاصل عدد 1 شود؟ درست حدس زدید: عدد 3- . الگوی بدست آمده از توضیحات بالا به صورت زیر می شود:

\(4n - 3\)

برای مطمئن شدن از الگوی n ام بدست آمده، فقط کافی است که مقادیر 2، 3 و ... را در رابطه گذاشته تا جمله های دوم، سوم و ... نیز بدست آید

2- الگو های شکلی و جمله n ام

در این الگوها با توجه به رابطه ای که بین شکل ها وجود دارد، می توان به جمله n ام و شکل مورد نظر رسید.

مثال

جمله n ام الگوی زیر را یافته و بنویسید. شکل دهم این الگو از چند چوب کبریت درست شده است؟

با دقت در شکل ها ملاحظه می شود تفاوت شکل دوم و اول ۳ چوب کبریت می باشد. همچنین تفاوت شکل سوم و دوم نیز 3 چوب کبریت می باشد . در نتیجه جمله n ام مضربی از عدد ۳ خواهد بود که یک واحد به آن اضافه شده است. پس جمله n ام این الگو برابر است با: \(3\,n\, + \,1\)

تعداد چوب کبریت های شکل دهم نیز به این صورت محاسبه می شود:

\(3\,(10)\, + \,1 = 31\)

در الگوی مقابل، شکل n ام چند چوب کبریت و چند مثلث دارد؟

با دقت در شکل ها متوجه می شویم تفاوت شکل بعدی با شکل فعلی، 2 عدد چوب کبریت است، پس شمار تعداد چوب ها از ضرب شماره هر شکل در عدد 2 با جمع یک مقدار ثابت بدست می آید که بعد از کمی دقت متوجه می شویم که این مقدار ثابت عدد 1 می باشد. پس شمار تعداد چوب کبریت های شکل n ام از رابطه زیر بدست می آید:

\(2n + 1\)

و تعداد مثلث در هر شکل با شماره آن شکل یکی است؛ بنابراین تعداد مثلث در شکل n ام برابر همان n می باشد.

3- جمله عمومی مسئله ها

در بعضی از مسائل محاسباتی مربوط به کار در شرکت ها و مکان های اداری، در آمد به صورت هزینه ثابت و هزینه متغیر با مقدار ساعت اضافه کاری محاسبه می شود. در این الگوها ابتدا هزینه ثابت را نوشته و هزینه دیگر را به عنوان ضریب n در نظر گرفته و به آن اضافه می کنیم.

مثال

یک شرکت حمل بار ۳۰۰۰۰ تومان در ابتدای فرداد و به ازای هر ساعت کار ۴۰۰۰ تومان دریافت می کند. برای n ساعت کار چقدر باید پول پرداخت؟

\(30000\, + \,4000\,\,n\,\)

حقوق ثابت رضا 700000 تومان است. اگر به ازای هر ساعت اضافه کاری 20000 تومان به او بدهند، به ازای n ساعت اضافه کاری در ماه، در پایان ماه، حقوق او به چه صورت محاسبه می شود؟

مقدار حقوق \(\; = 700,000\, + \,20,000\,\,n\,\) تومان

4- نوشتن دستور محاسبه محیط و مساحت به صورت جبری

برای این کار با توجه به دستور رسیدن به محیط و مساحت اشکال مختلف و حروفی که روی اضلاع آن شکل آمده، عمل می کنیم.

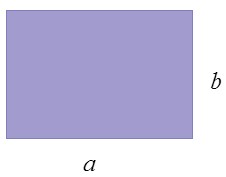
2× (عرض + طول) = محیط مستطیل عرض × طول = مساحت مستطیل

\(P\, = \,(a + b) \times 2\) \(S\, = \,a \times \,b\)

مثال

نسبت مساحت به محیط یک مستطیل به طول a و عرض b را به صورت جبری بدست آورید.

2× (عرض + طول) = محیط مستطیل عرض × طول = مساحت مستطیل

\(S\, = \,a \times \,b\) \(P\, = \,(a + b) \times 2\)

بنابراین:

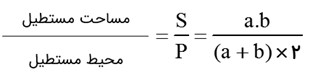
نسبت مساحت به محیط یک دایره را به شعاع R به صورت جبری بدست آورید.

مساحت دایره: \(\;S = \pi {R^2}\)

محیط دایره: \(P = 2\pi R\)

بنابراین:

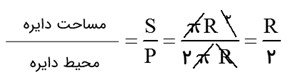
مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه هفتم

آزمون آنلاین تمامی دروس پایه هفتم
گام به گام تمامی دروس پایه هفتم
ویدئو های آموزشی تمامی دروس پایه هفتم
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
فلش کارت های آماده دروس پایه هفتم
گنجینه ای جامع از انشاء های آماده پایه هفتم
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

جمله جبری

جمله جبری، کوچکترین بخش از هر عبارت جبری را گویند که شامل دو بخش می باشد:

۱- ضریب عددی:

عددی است که در ابتدای هر جمله جبری قرار گرفته است.

۲- بخش حرفی:

حرف یا حروفی است که بعد از ضریب قرار می گیرند.

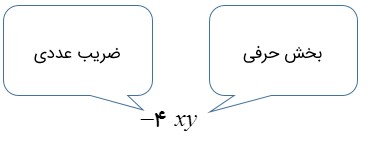
برای جلوگیری از اشتباه شدن علامت ضرب با حرف x در یک عبارت جبری، به جای علامت × از نقطه یا پرانتز و یا از قرار دادن این علامت بطور کلی صرف نظر می کنند؛ مانند:

\(3\, \times \,a\, \times \,b = 3\, \cdot \,a\, \cdot \,b = 3\,(\,a\, \cdot \,b) = 3ab\)

از نوشتن ضریب ۱ می توان صرف نظر کرد:

\(1\, \times \,a\, \times \,b = ab\)

اعداد به تنهایی و بدون حرف خود یک جمله ای جبری به حساب می آیند.

جزوات جامع پایه هفتم

جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله

جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح

جزوه جامع ریاضی هفتم فصل 3 جبر و معادله

جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال

جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول

جزوه جامع ریاضی هفتم فصل 6 سطح و حجم

جزوه جامع ریاضی هفتم فصل 7 توان و جذر

جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات

جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال

چند جمله ای

از کنار هم قرار گرفتن چند یک جمله ای که با علامت های جمع یا تفریق از هم جدا شده اند، به وجود می آید؛ مانند:

دو جمله ای\(8\, + \,x\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\)

چهار جمله ای \( - \,b\, - \,8\, + \,7\,x\,y + 2a\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\)

جمله های متشابه

عبارت های جبری هستند که بخش حرفی آنها مثل هم بوده و تفاوت آن ها در ضرایب عددی آنهاست؛ مانند:

\( - \,4\,x\;\;,\;\;\frac{1}{2}\,x\;\;,\;\;9\,x\;\;,\;\; \cdots \)

اعمال جمع، تفریق و ضرب در عبارت های جبری

جمع و تفریق در عبارت های جبری

برای این کار فقط می توان جمله های متشابه را با هم جمع یا از هم کم کرد؛ مانند :

\( - \,4\,x\, + \,5\,x\, - \,2\,x\, = \,(\, - \,4\, + \,5\, - \,2)\,x = \, - \,1\,x = - \,x\)

ساده کردن عبارت های جبری

برای ساده کردن یک عبارت جبری، ابتدا عملیاتی که بین جمله ها وجود دارند را انجام داده، سپس جمله های متشابه را با هم جمع یا از هم کم می کنیم.

اگر هنگام ساده کردن یک عبارت جبری، جمله ای متشابه نداشت، آن جمله را بدون تغییر در مراحل بعد می نویسیم.

ضرب عدد در عبارت جبری

1- ضرب عدد در یک جمله ای:

عدد در ضریب یک جمله ای ضرب می شود؛ مانند:

\( - 2 \times (3x) = - 6x\)

2- ضرب عدد در چند جمله ای:

عدد در تک تک ضرایب یک جمله ای ها ضرب می شود؛ مانند:

\( - 2 \times ( - 3x + 5y) = 6x - 10y\)

ضرب یک جمله ای در چند جمله ای

ابتدا علامت ها، بعد ضرایب عددی و سپس حروف در هم ضرب خواهند شد؛ مانند:

\(2a \times ( - 3x + 7y) = - 6ax + 14ay\)

مثال

عبارت های جبری زیر را ساده کنید.

الف \( - 4ab(\frac{1}{a} - \frac{3}{b}) - \frac{3}{{ab}}( - 2{a^2}b - \frac{4}{6}{b^2}a)\)

ب \( - 2{a^2}b( - 2b + a) + 3b{a^2}( + \frac{1}{3}b - 4a)\)

پ \( - ( - x - 2y - 3z) + 2(z + 2x + 3y) - 4(y - 2z - 3x)\)

الف

\(\begin{array}{l} - 4ab(\frac{1}{a} - \frac{3}{b}) - \frac{3}{{ab}}( - 2{a^2}b - \frac{4}{6}{b^2}a) = \\\underline { - 4b} + \underline{\underline {12a}} + \underline{\underline {6a}} + \underline {2b} = - 2b + 18a = 2(9a - b)\end{array}\)

\(\begin{array}{l} - 2{a^2}b( - 2b + a) + 3b{a^2}( + \frac{1}{3}b - 4a) = \\ + \underline {4{a^2}{b^2}} - \underline{\underline {2{a^3}b}} + \underline {{b^2}{a^2}} - \underline{\underline {12{a^3}b}} = \\5{b^2}{a^2} - 14{a^3}b = {a^2}b( - 14a + 5b)\end{array}\)

\(\begin{array}{l} - ( - x - 2y - 3z) + 2(z + 2x + 3y) - 4(y - 2z - 3x) = \\ + \underline x + \underline{\underline {2y}} + \underline{\underline {\underline {3z} }} + \underline{\underline {\underline {2z} }} + \underline {4x} + \underline{\underline {6y}} - \underline{\underline {4y}} + \underline{\underline {\underline {8z} }} + \underline {12x} = \\17x + 4y + 13z\end{array}\)

مقدار عددی عبارت جبری

برای تعیین این مقدار، به جای حروف موجود در عبارت، اعداد داده شده را می نویسیم؛ مانند:

مثال

مقدار عددی عبارت \(m( - 3m + 1)\) به ازای \(m = - 2\) به دست آورید.

\(\begin{array}{l}m( - 3m + 1)\mathop = \limits^{m = - 2} ( - 2)\left[ { - 3 \times ( - 2) + 1} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - 2 \times 7 = - 14\end{array}\)

اگر 5- = a و 4 = b باشد، حاصل عبارت \( - 3a(1 - b) + \frac{2}{3}b(2a - 1)\) برابر چه عددی می باشد؟

\(\begin{array}{l} - 3a(1 - b) + \frac{2}{3}b(2a - 1) = \\ - 3( - 5)(1 - 4) + \frac{2}{3} \times 4(2( - 5) - 1) = \\45 + \frac{2}{3}( - 44) = 45 - \frac{{88}}{3} = \frac{{135 - 88}}{3} = \frac{{47}}{3}\end{array}\)