درسنامه کامل ریاضی هفتم فصل 8 بردار و مختصات
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هفتم فصل 8 بردار و مختصات - درسنامه شب امتحان ریاضی هفتم فصل 8 بردار و مختصات - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 8 بردار و مختصات
بردار
شناخت بردار
حرکت و نیرو را با پاره خط های جهت دار نشان می دهیم.در ریاضی به پاره خط جهت دار بردار می گوییم. بردار OA را به صورت \(\overrightarrow {OA} \) نشان می دهیم.
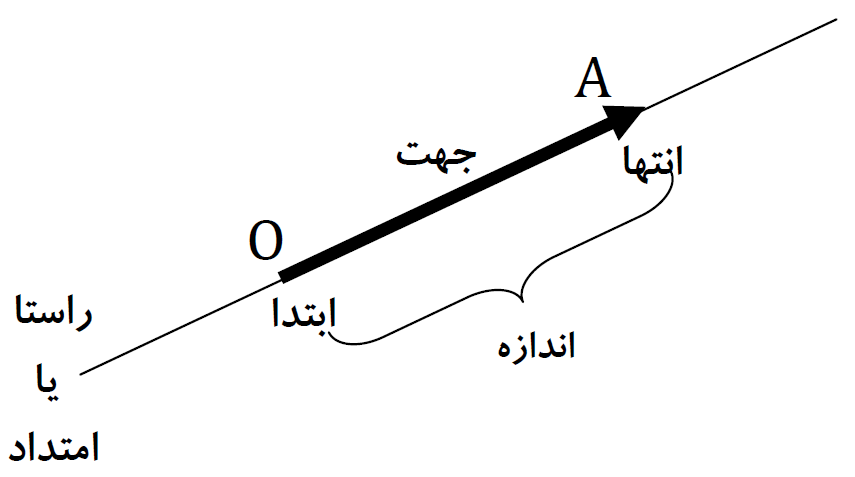
نام گذاری بردار
این کار به دو صورت انجام می شود:
الف) نخست نقطه ابتدا، سپس نقطه انتها را نوشته و نماد → را روی آن قرار دهید؛ مانند: \(\overrightarrow {AB} \)
\(A\;\; \to \;\;B\)
ب) با یک حرف کوچک لاتین که در وسط بردار قرار می گیرد، انجام می شود؛ مانند:
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
اندازه و انواع بردارها
اندازه (طول) بردار
برای رسیدن به اندازه بردار نخست به جهت حرکت بردار توجه نمایید (سمت راست + و سمت چپ -) و سپس تعداد واحد های بین ابتدا و انتهای بردار را بشمارید.
بردارهای مساوی
دو بردار وقتی برابرند که هم راستا هم اندازه و هم جهت باشند.
بردارهای قرینه
دو بردار وقتی قرینه یکدیگرند که مساوی باشند، اما در خلاف جهت هم حرکت کنند؛ مانند:
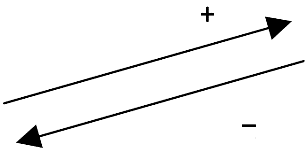
جمع دو بردار قرینه، همیشه صفر می شود.
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
مختصات
مختصات
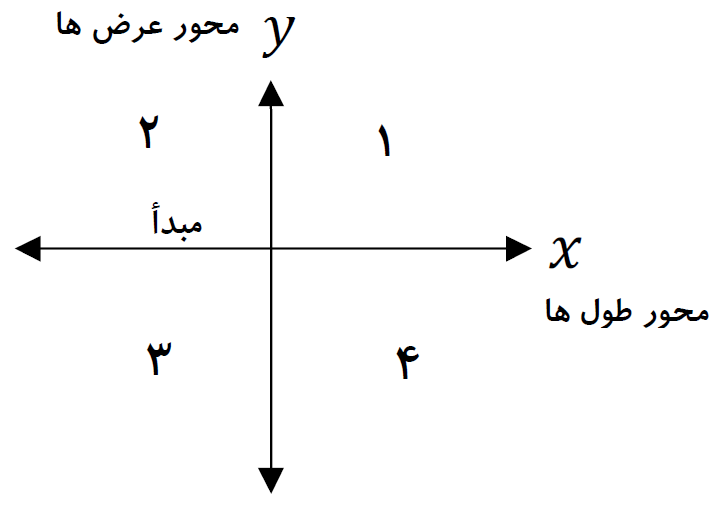
از دو محور عمود بر هم تشکیل می شود. محور افقی را محور طول ها (x ها) و محور عمودی را محور عرض ها (y ها) می نامند.
محل برخورد دو محور را «مبدأ مختصات» می نامند و با حرف O نمایش می دهند.
محورهای مختصات صفحه را به ۴ قسمت تقسیم می کنند.
در شکل مقابل این ۴ ناحیه با عددهای ۱ تا ۴ مشخص شده اند.
مختصات نقطه
به طول و عرض هر نقطه که به صورت \(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\) نمایش داده می شود، مختصات آن نقطه گفته می شود.
این مختصات می تواند + ، - یا حتی 0 باشد.
مختصات نقاط در ٤ قسمت:
1) اگر نقطه ای در قسمت ۱ (ربع یا ناحیه اول) قرار گرفته باشد، دارای طول و عرض مثبت می باشد:
\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& + \\y& + \end{array}} \right]\)قسمت 1
2) اگر نقطه در قسمت ۲ (ربع یا ناحیه دوم) قرار گرفته باشد، دارای طول منفی و عرض مثبت می باشد:
\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& - \\y& + \end{array}} \right]\)قسمت 2
3) اگر نقطه در قسمت ۳ (ربع یا ناحیه سوم) قرار گرفته باشد، دارای طول و عرض منفی می باشد:
\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& - \\y& - \end{array}} \right]\)قسمت 3
4) و اگر نقطه در قسمت ۴ (ربع یا ناحیه چهارم) قرار گرفته باشد، دارای طول مثبت و عرض منفی می باشد:
\(\;\; \to \;\;\left[ {\begin{array}{*{20}{c}}x& + \\y& - \end{array}} \right]\)قسمت 4
اگر نقطه ای روی محور طولها (x ها) قرار گرفته باشد، طول آن نقطه عدد و عرض آن 0 می شود.
1 تمام بردارهایی که موازی محور x ها باشند نیز دارای عرض 0 می باشند.
2 اگر نقطه ای روی محور عرض ها (y ها) قرار گرفته باشد، طول آن نقطه 0 و عرض آن عدد می شود.
3 تمام بردارهایی که موازی محور y ها باشند نیز دارای طول 0 می باشند.
مختصات مبدأ مختصات
محل برخورد محورهای مختصات را با حرف O نمایش می دهند و مختصات آن برابر است با: \(O = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\)
مثال
ناحیه نقاط زیر را بنویسد.
\(\begin{array}{l}1)\,\left[ {\begin{array}{*{20}{c}}1\\{ - 1}\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2)\,\left[ {\begin{array}{*{20}{c}}{ - 5}\\{ - 4/5}\end{array}} \right]\\\\3)\left[ \begin{array}{l}6\\5\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4)\left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\\\\5)\,\left[ {\begin{array}{*{20}{c}}{ - 1}\\1\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6)\left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right]\\\\7)\,\left[ {\begin{array}{*{20}{c}} \circ \\6\end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8)\left[ {\begin{array}{*{20}{c}}5\\5\end{array}} \right]\end{array}\)
1 ناحیه چهارم 2 ناحیه سوم 3 ناحیه اول
4 مرکز مختصات 5 ناحیه دوم 6 محور x های منفی
7 محور y های مثبت 8 ناحیه اول (بر روی نیم ساز ناحیه اول و سوم)
مثال
اگر نقطه \(\left[ {\begin{array}{*{20}{c}}{m + 6}\\{ - 3m - 5}\end{array}} \right]\) روی محور y ها باشد، مختصات نقطه را مشخص کنید.
هنگامی که مختصات نقطه ای بر روی محور y ها باشد، مؤلفه x آن برابر صفر خواهد بود:
\(m + 6 = 0 \Rightarrow m = - 6 \Rightarrow \left[ {\begin{array}{*{20}{c}} \circ \\{13}\end{array}} \right]\)
مثال
اگر فاصله نقطه \(\left[ {\begin{array}{*{20}{c}}{ - 4a + 1}\\{3a + 8}\end{array}} \right]\) از هر دو محور مختصات به یک فاصله باشد، مختصات نقطه را بیابید و ناحیه آن را مشخص کنید.
\(\begin{array}{l} - 4a + 1 = 3a + 8 \Rightarrow - 4a - 3a = 8 - 1\\\\ \Rightarrow - 7a = 7 \Rightarrow a = - 1 \Rightarrow \left[ \begin{array}{l}5\\5\end{array} \right]\end{array}\)
نقطه در ناحیه اول قرار دارد.
تهیه کننده: مسعود زیرکاری
اعمال ریاضی در بردارها
جمع متناظر بردار
در نوشتن جمع متناظر با یک بردار به مقدار ابتدا، اندازه و انتهای آن نیاز دارید تا با استفاده از دستور زیر بتوانید جمع متناظر بردار را بنویسید:
انتها = اندازه + ابتدا
بردار انتقال
به برداری گفته می شود که یک نقطه یا یک شکل را به اندازه مختصاتش (از ابتدا به انتها) منتقل نماید.
قرینه بردار
قرینه ابتدا و انتهای بردار مورد نظر را نسبت به مبدأ مختصات یا یکی از محورها (طول یا عرض) یافته و سپس بردار قرینه را رسم می کنیم.
قرینه بردار نسبت به محور طول ها
فقط عرض بردار قرینه می شود:
\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;x \to \;\left[ {\begin{array}{*{20}{c}}x\\{ - y}\end{array}} \right]\)
قرینه بردار نسبت به محور عض ها
فقط طول بردار قرینه می شود:
\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;y \to \;\left[ {\begin{array}{*{20}{c}}x\\{ - y}\end{array}} \right]\)
قرینه بردار نسبت به مبدأ مختصات
طول و عرض بردار هر دو قرینه می شود:
\(\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\;\;o \to \;\;\left[ {\begin{array}{*{20}{c}}{ - x}\\{ - y}\end{array}} \right]\)
مثال
مرکز پاره خط AB که در آن \(A = \left[ \begin{array}{l}5\\4\end{array} \right]\) و \(B = \left[ \begin{array}{l} - 3\\6\end{array} \right]\) را بیابید.
\(\begin{array}{l}\left. \begin{array}{l}A = \left[ \begin{array}{l}5\\4\end{array} \right] = \left[ \begin{array}{l}{x_A}\\{y_A}\end{array} \right]\\\\B = \left[ \begin{array}{l} - 3\\6\end{array} \right] = \left[ \begin{array}{l}{x_B}\\{y_B}\end{array} \right]\end{array} \right\} \Rightarrow M = \left[ \begin{array}{l}{x_M}\\{y_M}\end{array} \right]\\\\\left. \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{5 + ( - 3)}}{2} = \frac{2}{2} = 1\\\\{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{6 + 4}}{2} = \frac{{10}}{2} = 5\end{array} \right\} \Rightarrow M = \left[ \begin{array}{l}1\\5\end{array} \right]\end{array}\)
مثال
بردار \(\left[ \begin{array}{l}9 - 3x\\1 - \frac{y}{3}\end{array} \right]\) برداری است که ابتدا و انتهای آن روی هم قرار دارند؛ y + x را بدست آورید.
فقط بردار \(\overrightarrow O = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\) ابتدا و انتهای آن روی هم قرار دارند؛ بنابراین:
\(\begin{array}{l}\left[ \begin{array}{l}9 - 3x\\1 - \frac{y}{3}\end{array} \right] = \left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right] \Rightarrow \left\{ \begin{array}{l}9 - 3x = 0 \Rightarrow 9 = 3x \Rightarrow x = 3\\\\1 - \frac{y}{3} = 0 \Rightarrow 1 = \frac{y}{3} \Rightarrow y = 3\end{array} \right.\\\\ \Rightarrow x + y = 6\end{array}\)
مثال
قرینه بردارهای زیر را نسبت به مرکز و یا محور داده شده مشخص کنید.
\(\begin{array}{l}1)\,\,\left[ \begin{array}{l} - 2\\4\end{array} \right]\,\,\,\,\,\,\,\,\,\,y \to \\\\2)\,\,\left[ \begin{array}{l}5\\ - 3\end{array} \right]\,\,\,\,\,\,\,\,\,\,x \to \\\\3)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,y \to \\\\4)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,x \to \\\\5)\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \\\\6)\,\,\left[ \begin{array}{l} - 10\\ + 3\end{array} \right]\,\,\,\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \end{array}\)
\(\begin{array}{l}1)\,\,\left[ \begin{array}{l} - 2\\4\end{array} \right]\,\,\,\,\,\,y \to \,\,\,\,\,\,\left[ \begin{array}{l}2\\4\end{array} \right]\\\\2)\,\,\left[ \begin{array}{l}5\\ - 3\end{array} \right]\,\,\,\,\,\,\,x \to \,\,\,\,\left[ \begin{array}{l}5\\3\end{array} \right]\\\\3)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\,\,y \to \,\,\,\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\\\\4)\,\,\left[ \begin{array}{l} - 15\\ - 20\end{array} \right]\,\,\,\,\,\,\,x \to \,\,\,\,\,\left[ \begin{array}{l} - 15\\20\end{array} \right]\\\\5)\,\,\left[ \begin{array}{l}15\\ - 20\end{array} \right]\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \,\,\,\,\left[ \begin{array}{l} - 15\\20\end{array} \right]\\\\6)\,\,\left[ \begin{array}{l} - 10\\ + 3\end{array} \right]\,\,\,\,\,\,\,\left[ \begin{array}{l} \circ \\ \circ \end{array} \right] \to \,\,\,\,\left[ \begin{array}{l} + 10\\ - 3\end{array} \right]\end{array}\)
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
یافتن مقدار مجهول در تساوی های برداری
یافتن مقدار مجهول در تساوی های برداری
اگر مقدار مجهول (نامعلوم) در انتهای تساوی برداری بود، مقدارهای ابتدا و اندازه را با هم جمع کنید؛ مانند:
\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}2\\{ - 4}\end{array}} \right]\;\; + \left[ {\begin{array}{*{20}{c}}{ - 3}\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\\\\\left. \begin{array}{l}x = 2 + ( - 3) = - 1\\y = ( - 4) + 1 = - 3\end{array} \right\}\;\; \Rightarrow \;\;\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 3}\end{array}} \right]\end{array}\)
اگر مقدار مجهول (نامعلوم) در ابتدا یا اندازه تساوی برداری قرار گرفته بود، مقدار انتها را منهای قسمت دیگر کنید:
\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}2\\{ - y}\end{array}} \right]\;\; + \left[ {\begin{array}{*{20}{c}}{ - x}\\{ - 2}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 2}\\3\end{array}} \right]\\\\\left. \begin{array}{l} - x = ( - 2) - 2 = - 4\\ - y = 3 - ( - 2) = 5\end{array} \right\}\; \Rightarrow \,\,\left. \begin{array}{l}x = 4\\y = - 5\end{array} \right\}\,\, \Rightarrow \;\;\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}4\\{ - 5}\end{array}} \right]\end{array}\)
مثال
اگر \(A = \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right]\,\,,\,\,B = \left[ {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right]\) و \(2\overrightarrow {BA} + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right]\) ، مختصات نقطه C را بدست آورید.
ابتدا بردار \(\overrightarrow {AC} \) را بدست می آوریم:
\(\begin{array}{l}\overrightarrow {BA} = \overrightarrow {OA} - \overrightarrow {OB} = \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 2}\\2\end{array}} \right]\\\\2\overrightarrow {BA} + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] \Rightarrow 2\left[ {\begin{array}{*{20}{c}}{ - 2}\\2\end{array}} \right] + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right]\\\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{ - 4}\\4\end{array}} \right] + \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] \Rightarrow \overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\4\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}{ - 4}\\4\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right]\\\\\overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} \Rightarrow \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right] = \overrightarrow {OC} - \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right]\\\\ \Rightarrow \overrightarrow {OC} = \left[ {\begin{array}{*{20}{c}}{ - 1}\\ \circ \end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{ - 4}\\3\end{array}} \right] \Rightarrow \overrightarrow {OC} = \left[ {\begin{array}{*{20}{c}}{ - 5}\\3\end{array}} \right] \Rightarrow C = \left[ {\begin{array}{*{20}{c}}{ - 5}\\3\end{array}} \right]\end{array}\)
مثال
اگر \(\left[ {\begin{array}{*{20}{c}}{4x + 3}\\{7 + y}\end{array}} \right]\, = \left[ {\begin{array}{*{20}{c}}{x - 3}\\{10 - 2y}\end{array}} \right]\) ، حاصل \(\frac{{3x - 1}}{{4y + 2}}\) کدام است؟
\(\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{4x + 3}\\{7 + y}\end{array}} \right]\, = \left[ {\begin{array}{*{20}{c}}{x - 3}\\{10 - 2y}\end{array}} \right]\\\\4x + 3 = x - 3 \Rightarrow 3x = - 3 \Rightarrow x = - 1\\\\7 + y = 10 - 2y \Rightarrow 3y = - 3 \Rightarrow y = - 1\\\\ \Rightarrow \frac{{3x - 1}}{{4y + 2}} = \frac{{3( - 1) - 1}}{{4( - 1) + 2}} = \frac{{ - 4}}{{ - 2}} = 2\end{array}\)
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
تعیین مختصات بردار به کمک ترسیم
تعیین مختصات بردار به کمک ترسیم
از ابتدا و انتهای بردار، دو خط به موازات محور طول و عرض به ترتیب رسم کنید تا در نقطه ای یکدیگر را قطع کنند و تشکیل یک مثلث قائم الزاویه دهند. حالا از ابتدا به سمت انتهای بردار حرکت کنید تا هم جهت و هم مختصات آن را مشخص کنید؛ مانند:
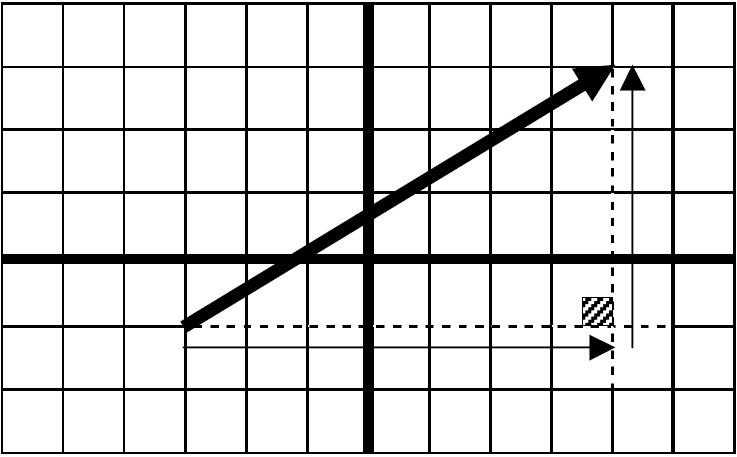
می بینید از ابتدای بردار ۷ واحد به سمت راست حرکت کرده ایم، یعنی ۷+ و 4+ واحد نیز به سمت بالا حرکت کرده ایم؛ پس مختصات بردار مورد نظر \(\left[ {\begin{array}{*{20}{c}}{ + 7}\\{ + 4}\end{array}} \right]\) خواهد بود.
مثال
بردار خواسته شده را رسم کنید.
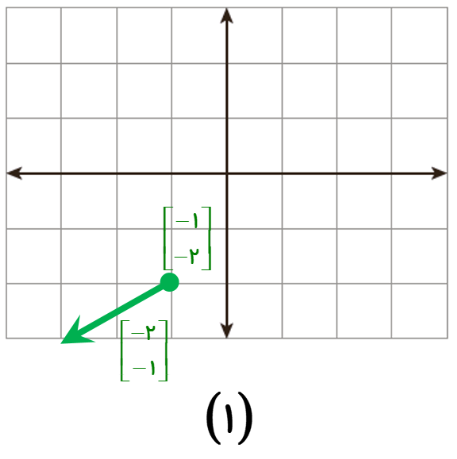
1 بردار \(\left[ {\begin{array}{*{20}{c}}{ - 2}\\{ - 1}\end{array}} \right]\) ابتدا در \(\left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 2}\end{array}} \right]\)
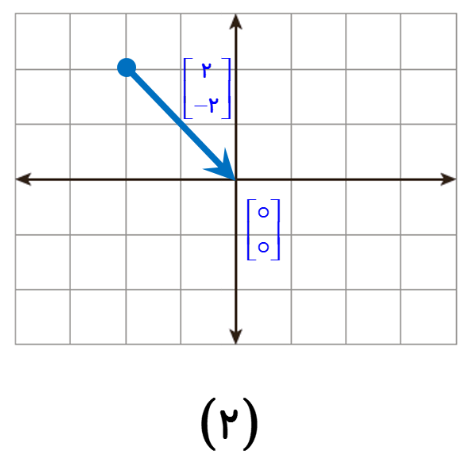
2 بردار \(\left[ {\begin{array}{*{20}{c}}2\\{ - 2}\end{array}} \right]\) انتها در \(\left[ {\begin{array}{*{20}{c}} \circ \\ \circ \end{array}} \right]\)
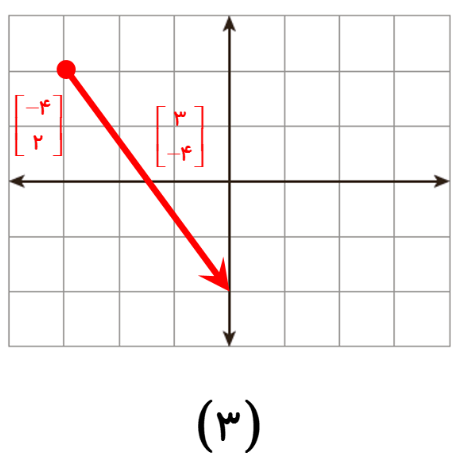
3 بردار \(\left[ {\begin{array}{*{20}{c}}3\\{ - 4}\end{array}} \right]\) ابتدا در \(\left[ {\begin{array}{*{20}{c}}{ - 4}\\2\end{array}} \right]\)
تهیه کننده:مسعود زیرکاری



1736019749.png)