درسنامه کامل ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
تعداد بازدید : 7.25Mخلاصه نکات ریاضی هفتم فصل 5 شمارنده ها و اعداد اول - درسنامه شب امتحان ریاضی هفتم فصل 5 شمارنده ها و اعداد اول - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 5 شمارنده ها و اعداد اول
شمارنده ها و اعداد اول
شمارنده ها (مقسوم علیه های) یک عدد
در ریاضیات اگر عددی طبیعی مانند a بر عددی طبیعی مانند b بخش پذیر باشد، b را شمارنده یا مقسوم علیه a گویند. به بیان دیگر باقیمانده a بر b برابر صفر می شود؛ مانند: 1، 2، 3، ۶ و ۱۲ که همگی شمارنده های عدد ۱۲ می باشند.
12 و 6 و 4 و 3 و 2 و 1= شمارنده های ۱۲
عدد اول
اعداد طبیعی هستند که فقط دو شمارنده دارند، یکی عدد ۱ و دیگری خود عدد؛ مانند:
۱ و ۱۱ = شمارنده های ۱۱
۱ و ۲ = شمارنده های ۲
عدد ۱ نه اول است و نه غیر اول (مرکب)، بلکه به آن «بسیط» یا «ساده» می گویند.
شمارنده های اول
به شمارنده هایی که عدد اول باشند، «شمارنده های اول» گفته می شود.
برای رسیدن به شمارنده های اول می توان از روش های زیر استفاده کرد:
۱) نوشتن تمامی شمارنده های عدد مورد نظر و مشخص کردن شمارنده های اول آن.
۲) استفاده از نمودار درختی یا تجزیه کردن (نوشتن عدد به صورت ضرب عامل های اول
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
استفاده از قواعد بخش پذیری اعداد اول
1- بخش پذیری بر ۲:
یکان عدد زوج باشد.
2- بخش پذیری بر ۳:
جمع رقم ها مضرب ۳ باشد.
3- بخش پذیری بر ۴:
دو برابر دهگان را با یکان جمع می کنیم و باقیمانده ی تقسیم عدد حاصل بر ۴ را به دست می آوریم. اگر باقیمانده صفر شد. عدد بر ۴ بخش پذیر است.
باقیمانده تقسیم عدد 14 بر 4 برابر 2 می باشد\(2\underline 5 4\;\; \to \;\;2 \times 5 + 4 = 10 + 4 = 14\;\; \Rightarrow \;\;\)
4- بخش پذیری بر ۵:
یکان 0 یا ۵ باشد.
5- بخش پذیری بر ۶:
اعداد زوجی که بر 3 بخش پذیر باشد بر ۶ بخش پذیرند. در واقع اگر عددی هم بر ۲ و هم بر ۳ بخش پذیر است، بر ۶ نیز بخش پذیر خواهد بود.
1 حاصل ضرب سه عدد متوالی بر 6 بخش پذیر است:
\(\begin{array}{l}(2,\,3,\,4)\;\;\;\;\;\;\;\;\;\;\;\;\;\;2 \times 3 \times 4 = 24\\(3,\,4,\,5)\;\;\;\;\;\;\;\;\;\;\;\;\;\;3 \times 4 \times 5 = 60\end{array} \)
2 حاصل ضرب دو عدد فرد یک عدد فرد است.
\(3 \times 5 = 15\)
3 حاصل ضرب دو عدد زوج یک عدد زوج است.
\(2 \times 12 = 24\)
4 حاصل ضرب یک عدد زوج در یک عدد فرد، یک عدد زوج است.
\(5 \times 4 = 20\)
6- بخش پذیری بر ۷:
عدد حاصل از مجموع پنج برابر یکان و بقیه رقم ها، مضرب ۷ باشد؛ مانند:
\(231\;\,\, \to \;\;(1 \times 5) + 23 = 28 = 14\;\,\, \to \;\;28 = 7 \times 4\)
7- بخش پذیری بر ۹:
جمع رقم ها مضرب ۹ باشد.
8- بخش پذیری بر ۱۱:
الف) دو رقمی:
ارقام تکراری؛ مانند : ۷۷ یا ۴۴
ب) سه رقمی:
رقم وسط برابر جمع دو رقم کناری شود؛ مانند: ۱۷۶ یا ۳۵۲ و ... .
پ) چند رقمی:
رقم های عدد مورد نظر را یکی در میان جمع می کنیم. حاصل جمع دو گروه را از هم کم می کنیم. اگر این حاصل 0 یا مضرب ۱۱ شد، عدد پر ۱۱ بخش پذیر می باشد.
\(4136\,\,\,\;\;\left. \begin{array}{l}4 + 3 = 7\\1 + 6 = 7\end{array} \right\}\, \Rightarrow \,7 - 7 = 0\)
9- بخش پذیری بر ۱۳:
حاصل مجموع چهار برابر یکان و بقيه رقم ها، مضرب ۱۳ باشد؛ مانند:
\(65\;\,\, \to \;\;(5 \times 4) + 6 = 26\;\,\, \to \;\;26 = 13 \times 2\)
مثال
مجموع سه عدد فرد متوالی همواره بر کدام یک از عددهای اول تک رقمی بخش پذیر است؟
: مجموع سع عدد فرد متوالی
\((2k + 1) + (2k + 3) + (2k + 5) = 6k + 9 = 3(2k + 3)\)
پس مجموع سه عدد فرد متوالی بر 3 بخش پذیر است.
مثال
مقدار x چند باشد تا عدد نُه رقمی \(\overline {b458abxa5} \) بر 11 بخش پذیر باشد؟
در بخش پذیری بر عدد 11 داشتبم که رقم های عدد را از سمت راست شماره گذاری می کنیم. مجموع رقم های شماره فرد را از مجموع رقم های شماره زوج کم می کنیم. عدد حاصل باید بر 11 بخش پذیر باشد:
\(a + b + 8 + 4 = a + b + 12\) : مجموع رقم های شماره زوج
\(5 + x + a + 5 + b = x + a + b + 10\) : مجموع رقم های شماره فرد
= مجموع رقم های شماره فرد – مجموع رقم های شماره زوج
\((a + b + 12) - (x + a + b + 10) = 2 - x\)
حال عبارت بدست آمده باید صفر و یا مضربی از عدد 11 باشد و چون x یک عدد تک رقمی است، پس حاصل x – 2 بایستی صفر باشد. در نتیجه:
\(2 - x = 0 \Rightarrow x = 2\)
اگر x11 بر y7 بخش پذیر باشد، چه نتیجه ای می توان گرفت؟
x11 بر y7 بخش پذیر است. چون دو عدد 11 و 7 عامل مشترک ندارند (عدد اول هستند)، باید x عددی باشد که بعد از ضرب شدن در 11 بر y7 بخش پذیر شود؛ پس x حتما بر 7 بخش پذیر خواهد بود.
اگر عدد \(\overline {854x3y} \) بر 6 بخش پذیر باشد، بیشترین مقدار y + x را بیابید.
عددی که بر 6 بخش پذیر است، 2 شرط دارد:
شرط اول: عدد زوج باشد، یعنی بر 2 بخش پذیر باشد؛ در نتیجه y زوج می باشد.
شرط دوم: عدد مورد نظر بر 3 نیز بخش پذیر باشد؛ بنابراین:
\(\begin{array}{l}8 + 5 + 4 + x + 3 + y = 20 + x + y\\ \Rightarrow \\x + y = 1\\x + y = 4\\x + y = 7\\x + y = 10\\x + y = 13\\x + y = 16 \to x = 8\,\,\,\,\,,\,\,\,\,\,y = 8\end{array}\)
بیشترین مقدار برای y + x ، 16 است.
اگر حاصل ضرب دو عدد اوّل 91 باشد، حاصل جمع آن ها را بیابید.
\(91 = 13 \times 7 \Rightarrow 13 + 7 = 20\)
به چند حالت می توان با 28 دانش آموز تعدادی صف تشکیل داد؟
به 7 حالت می توان با 28 دانش آموز صف تشکیل داد. \(28 = \left\{ \begin{array}{l}28 \times 1\\14 \times 2\\7 \times 4\\4 \times 7\\2 \times 14\\1 \times 28\end{array} \right. \Rightarrow \)
در الگوریتم غربال برای تعیین اعداد اول 1 تا 100، پنجاه و هفتمین عددی که خط می خورد، کدام است؟
در ابتدا عدد 1 و سپس مضرب های 2 (به غیر از خود عدد 2) خط می خورند (تا الان 50 عدد خط خورده اند و می ماند 7 عدد دیگر تا به جواب برسیم). سپس همه مضرب هایی از 3 که بار اول خط نخورده اند (طبیعتاً به غیر از خود عدد 3) و بعد از پنجاهمین عدد قرار دارند، خط می خورند. در نتیجه پنجاه و هفتمین عدد، 45 است:
\(\begin{array}{*{20}{c}}9&{15}&{21}&{27}&{33}&{39}&{45}\\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow \\{51}&{52}&{53}&{54}&{55}&{56}&{57}\end{array}\)
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
ب.م.م، ک.م.م و نمودار درختی
بزرگ ترین شمارنده مشترک (ب.م.م)
شمارنده های یک عدد را مقسوم علیه های آن نیز می گویند؛ بنابراین بزرگ ترین شمارنده مشترک دو عدد همان بزرگ ترین مقسوم علیه مشترک است که به اختصار آن را ب.م.م می نویسند. ب.م.م دو عدد را به صورت \((\,\,\,\,\,,\,\,\,\,\,)\) نشان می دهند.
کوچک ترین مضرب مشترک (ک.م.م)
کوچک ترین مضرب مشترک دو عدد، اولین مضرب مشترک آن دو عدد است. کوچک ترین مضرب مشترک دو عدد را به طور اختصار ک.م.م می گویند و به صورت \(\left[ {\,\,\,\,\,,\,\,\,\,\,} \right]\) نمایش می دهند.
دستور برای یافتن ب.م.م و ک.م.م
پس از تجزیه عددها به شمارنده های اول آنها از دستورهای زیر برای یافتن ب.م.م و ک.م.م استفاده می کنیم:
ب.م.م \((\,\,\,\,\,,\,\,\,\,\,)\) :
شمارنده های مشترک با کمترین تکرار
ک.م.م \(\left[ {\,\,\,\,\,,\,\,\,\,\,} \right]\) :
شمارنده های غیر مشترک x شمارنده های مشترک با بیشترین تکرار
نمودار درختی
هرگاه عددی طبیعی را به صورت ضرب دو عدد غیر از ۱ به دوشاخه در آوریم (بهتر است این ضرب از یک عدد اول و یک عدد غير اول تشکیل شود) و این کار را ادامه دهیم، به شمارنده های اول آن عدد خواهیم رسید؛ مانند:
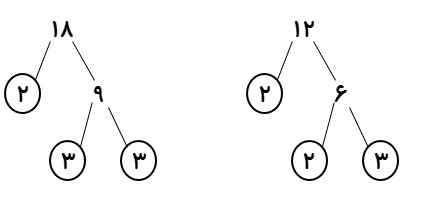
\(\begin{array}{l}18 = 2 \times 3 \times 3\\\\12 = 2 \times 2 \times 3\\\\\left( {18\;,\;12} \right) = 2 \times 3 = 6\\\\\left[ {18\;,\;12} \right] = 2 \times 2 \times 3 \times 3 = 36\end{array}\)
مثال
بزرگ ترین مقسوم علیه مشترک دو عدد A و B را بیابید.
\(\left\{ \begin{array}{l}A = {2^2} \times {3^3} \times 5\\B = 2 \times 3 \times {5^2}\end{array} \right.\)
\(\left\{ \begin{array}{l}A = {2^2} \times {3^3} \times 5\\B = 2 \times 3 \times {5^2}\end{array} \right. \Rightarrow \left( {A\,,\,B} \right) = 2 \times 3 \times 5 = 30\)
ک.م.م دو عدد 48 و 36 را بیابید.
\(\left\{ \begin{array}{l}48 = {2^4} \times 3\\36 = {2^2} \times {3^2}\end{array} \right. \Rightarrow \left[ {48\,,\,36} \right] = {2^4} \times {3^2} = 144\)
نمودار درختی دو عدد 144 و 96 را رسم کرده، ب.م.م و ک.م.م هر دو عدد را مشخص کنید.
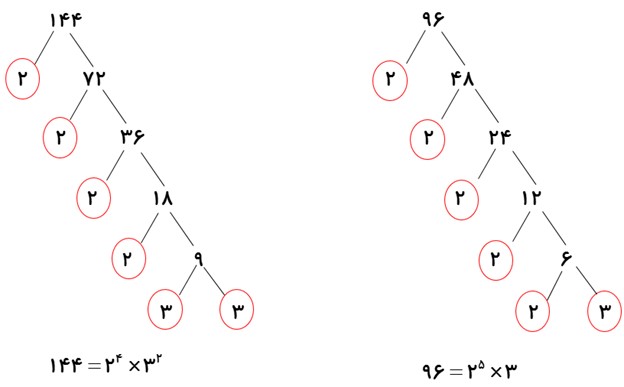
\(\left. \begin{array}{l}144 = {2^4} \times {3^2}\\\\96 = {2^5} \times 3\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\left( {144\,,\,96} \right) = {2^4} \times 3 = 48\\\\\left[ {144\,,\,96} \right] = {2^5} \times {3^2} = 288\end{array} \right.\)
مهم ترین کاربرد شمارنده های اول
ساده کردن کسرها
از مهم ترین کاربرد شمارنده های اول، ساده کردن کسرها می باشد. برای این منظور صورت و مخرج کسر را به شمارنده های اول آن تجزیه و سپس شمارنده های مشترک در صورت و مخرج را حذف می کنیم؛ مانند:
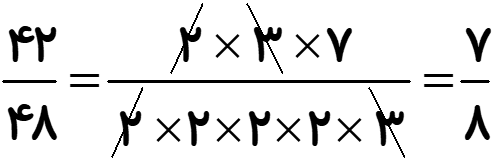
هم مخرج کردن کسرها
یکی از مهم ترین کاربردهای ک.م.م در پیدا کردن مخرج مشترک دو کسر است، یعنی کوچک ترین عددی را پیدا می کنیم که به هر دو مخرج بخش پذیر (قابل قسمت) باشد؛ مانند:
\(\begin{array}{l}\frac{{15}}{{12}} - \frac{7}{{18}} = \\18 = 2 \times 3 \times 3\\12 = 2 \times 2 \times 3\\\left[ {18\,,\,12} \right] = 2 \times 2 \times 3 \times 3 = 36\\\frac{{15}}{{12}} - \frac{7}{{18}} = \frac{{45}}{{36}} - \frac{{14}}{{36}} = \frac{{31}}{{36}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
نکاتی درباره ب.م.م و ک.م.م
1 ب.م.م هر عدد با ۱، 1 می شود.
\(\left( {9\,,\,1} \right) = 1 \)
2 ک.م.م هر عدد با ۱، خود عدد می شود.
\(\left[ {1\,,\,12} \right] = 12\)
3 ب. م. م هر عدد با خودش، همان عدد می شود.
\(\left( {15\,,\,15} \right) = 15\)
4 ک.م.م هر عدد با خودش خود همان عدد می شود.
\(\left[ {7\,,\,7} \right] = 7\)
5 ب.م.م دو عدد اول ۱ می شود.
\(\left( {5\,,\,11} \right) = 1\)
6 ک.م.م دو عدد اول، حاصل ضرب آنها می شود.
\(\left[ {7\,,\,13} \right] = 91\)
7 ب. م. م دو عدد بخش پذیر عدد کوچکتر می شود.
\(\left( {7\,,\,35} \right) = 7\)
8 ک.م.م دو عدد بخش پذیر، عدد بزرگتر می شود.
\(\left[ {36\,,\,12} \right] = 36\)
9 ب.م.م دو عدد متوالی، ۱ می شود.
\(\left( {5\,,\,6} \right) = 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {18\,,\,19} \right) = 1\)
10 ک.م.م دو عدد متوالی، حاصل ضرب آنها می شود.
\(\left[ {8\,,\,9} \right] = 72\)
مثال
اگر a بر b بخش پذیر باشد، حاصل عبارت \(\left[ {\left( {ab\,,\,a} \right),\left( {ab\,,\,b} \right)} \right]\) را بیابید.
هرگاه a بر b بخش پذیر باشد، آنگاه a مضربی از b و همچنین b مقسوم علیه a خواهد بود؛ بنابراین:
\(\begin{array}{l}\left( {ab\,,\,a} \right) = a\\\\\left( {ab\,,\,b} \right) = b\\\\ \Rightarrow \left[ {\left( {ab\,,\,a} \right),\left( {ab\,,\,b} \right)} \right] = \left[ {a,b} \right] = a\end{array}\)
اگر \(\left[ {a\,,\,b} \right] = 36\,,\,\left( {a\,,\,b} \right) = 6\,,\,b > a\) و 30 = b + a باشد، حاصل b – a3 را بیابید.
از آنجایی که \(\left( {a\,,\,b} \right) = 6\) در نتیجه a و b مضربی از عدد 6 خواهند بود. همچنین چون مجموع آن دو برابر عدد 30 می شود، پس کوچکتر از عدد 30 خواهند بود؛ یعنی از اعداد 6، 12، 18 و 24 خواهند بود.
همچنین چون \(\left[ {a\,,\,b} \right] = 36\) می شود، بنابراین جزو اعداد 12 و 18 می باشند؛ در نتیجه:
\(\left. \begin{array}{l}\left( {a\,,\,b} \right) = 6 = 2 \times 3\\\\\left[ {a\,,\,b} \right] = 36 = {2^2} \times {3^2}\\\\a > b\\\\a + b = 30\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}a = 12\\\\b = 18\end{array} \right.\)
بنابراین حاصل عبارت خواسته شده برابر است با:
\(3a - b = 3 \times 12 - 18 = 18\)
اگر \(\left[ {a\,,\,b} \right] = a \times b\) و \(\frac{b}{a} = \frac{{144}}{{96}}\) ، حاصل عبارت b + a2 را بیابید.
هنگامی که ک.م.م دو عدد برابر حاصل ضرب یک دیگر هستند، در نتیجه نسبت به یکدیگر اول هستند. بنابراین اگر کسر داده شده را ساده کنیم، مقادیر مجهول را پیدا کرده ایم:
\(\begin{array}{l}\frac{b}{a} = \frac{{144}}{{96}} = \frac{3}{2} \Rightarrow \left\{ \begin{array}{l}a = 2\\\\b = 3\end{array} \right.\\\\ \Rightarrow 2a + b = 2 \times 2 + 3 = 7\end{array}\)



1736019749.png)















