درسنامه کامل ریاضی هفتم فصل 4 هندسه و استدلال
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هفتم فصل 4 هندسه و استدلال - درسنامه شب امتحان ریاضی هفتم فصل 4 هندسه و استدلال - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 4 هندسه و استدلال
خط
خط از کنار هم قرار گرفتن بی شمار نقطه در کنار هم به وجود می آید.
انواع خط
1- خط راست.
2- خط شکسته.
3- خط خمیده (منحنی).

نام گذاری نقطه و خط
در ریاضیات برای نام گذاری شکل ها از حروف انگلیسی استفاده می کنیم. به طور معمول نقطه را با حروف بزرگ انگلیسی نام گذاری می کنیم و برای نام گذاری امتداد خط که در شکل با فلش نشان می دهیم از حروف کوچک استفاده می کنیم؛ مانند:

از یک نقطه بی شمار خط می گذرد.
از دو نقطه فقط یک خط راست می گذرد.
از دو نقطه بی شمار خط خمیده و شکسته می گذرد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
پاره خط و نیم خط
پاره خط
قسمتی از یک خط که با دو نقطه جدا شده باشد.
طول یا اندازه پاره خط:
طول یک پاره خط را با قرار دادن یک پاره خط کوچک در بالای نام آن نمایش می دهیم؛ برای مثال \(\overline {AB} \) یعنی طول پاره خط AB و آن فاصله بین دو سر پاره خط می باشد که با واحدی به نام سانتیمتر (cm) اندازه گیری می شود.
تعداد تمام پاره خط های روی یک خط از این دستور محاسبه می شود:
\(\frac{{n(n - 1)}}{2}\)
در این فرمول n تعداد نقطه ها می باشد.
مثال
اگر روی خطی 7 نقطه قرار دهیم، چند پاره خط روی آن ایجاد می شود؟
در این مثال 7 نقطه داریم (7 = n):
تعداد پاره خط ها \( = \frac{{n(n - 1)}}{2} = \frac{{7(7 - 1)}}{2} = \frac{{7 \times 6}}{2} = 21\)
روی خطی n نقطه قرار دارد. اگر 3 نقطه به این n نقطه اضافه کنیم، چند پاره خط به تعداد پاره خط ها اضافه می شود؟
ابتدا تعداد پاره خط ها را در هر حالت بدست می آوریم:
تعداد نقطه : حالت اول \( = n \Rightarrow \) تعداد پاره خط ها \( = \frac{{n(n - 1)}}{2}\)
عداد نقطه : حالت دوم \( = n + 3 \Rightarrow \) تعداد پاره خط ها \( = \frac{{(n + 3)(n + 3 - 1)}}{2}\)
تعداد پاره خط های اضافه شده \( = \frac{{(n + 3)(n + 2)}}{2} - \frac{{n(n - 1)}}{2}\)
\( = \frac{{{n^2} + 5n + 6 - {n^2} + n}}{2} = \frac{{4n + 6}}{2} = 2n + 3\)
تعداد 3 + n2 پاره خط اضافه می شود.
نیم خط
قسمتی از یک خط که از یک طرف با یک نقطه جدا شده باشد . نیم خط را ابتدا با نام نقطه و سپس نام خط نام گذاری می کنند و می خوانند؛ مانند نیم خط Ax
تعداد تمام نیم خط های روی یک خط از دستور n2 به دست می آید که در آن n تعداد نقطه ها می باشد.
مثال
اگر روی خطی 6 نقطه قرار دهیم، چند نیم خط ایجاد می شود؟
12 = 6 × 2 = تعداد نیم خط ها
در شکل مقابل چند پاره خط وجود دارد؟

از آنجایی که روی هر پاره خط افقی 6 نقطه وجود دارد، با توجه به مطالب بالا، تعداد پاره خط های روی آن ها برابر است با:
\(\frac{{n(n - 1)}}{2} = \frac{{6(6 - 1)}}{2} = 15\)
تعداد کل پاره خط های افقی \( = 5 \times 15 = 75\)
از طرفی 6 پارخط عمودی داریم که روی هر یک از آن ها 5 نقطه وجود دارد:
\(\frac{{n(n - 1)}}{2} = \frac{{5(5 - 1)}}{2} = 10\)
تعداد کل پاره خط های عمودی \( = 6 \times 10 = 60\)
در مجموع، تعداد کل پاره خط ها به صورت زیر محاسبه می شود:
تعداد کل پاره خط ها \( = 75 + 60 = 135\)
مقایسه پاره خط ها
پاره خط ها را با توجه به طول آنها با هم مقایسه می کنیم.
مثلا پاره خط AB بزرگتر از پاره خط EF می باشد. این موضوع را به صورت ریاضی چنین می نویسیم.

جمع و تفریق پاره خط ها
در جمع پاره خط ها به دنبال هم و در تفریق، آنها را روی هم قرار می دهیم؛ مانند:

در شکل نقاطA،B و C روی یک خط قرار دارند. داریم:
\(\begin{array}{l}AB + BC = AC\\AC - AB = BC\\AC - BC = AB\end{array}\)
نسبت بین پاره خط ها
با توجه به طول پاره خط ها می توان بین آنها نسبت های مختلفی به دست آورد؛ مانند:

در شکل M وسط پاره خط AB است.
\(\begin{array}{l}\overline {AB} = 2\overline {MB} \\\overline {AM} = \frac{1}{2}\overline {AB} \end{array}\)
روابط بین پاره خط ها
با شناخت رابطه بین چند پاره خط ها می توان به رابطه های دیگری رسید؛ مانند:
\(\left. \begin{array}{l}\overline {AB} = \overline {CD} \\\overline {AB} > \overline {EF} \end{array} \right\}\;\;\;\; \Rightarrow \;\;\;\;\overline {CD} > \overline {EF} \)
مثال
در شکل زیر، طول نقاط A و B مشخص شده است. اگر \(\overline {AB} = 2\overline {BC} \) و \(\overline {BC} = 3\overline {CD} \) باشد، طول نقاط C و D کدام است؟

روی محور اعداد صحیح، طول نقطه A را با xA نشان می دهند:
\(\begin{array}{l}\overline {AB} = {x_B} - {x_A} = 10 - 4 = 6\\\overline {AB} = 2\overline {BC} = 6 \Rightarrow \overline {BC} = 3\\\overline {BC} = 3\overline {CD} = 3 \Rightarrow \overline {CD} = 1\\\overline {BC} = 3 \Rightarrow {x_C} - {x_B} = {x_C} - 10 = 3 \Rightarrow {x_C} = 13\\\overline {CD} = 1 \Rightarrow {x_D} - {x_C} = {x_D} - 13 = 1 \Rightarrow {x_D} = 14\end{array}\)
دو خطی که بر خط سومی عمود باشند، نسبت به هم .......... .
موازی هستند.
می خواهیم یک طناب 30 متری را به بیشترین قطعات ممکن با طول هایی که عدد طبیعی بیشتر از 1 هستند، تقسیم کنیم. چند برش لازم داریم؟
هر قطعه طناب می تواند 2 متر باشد؛ یعنی 15 قطعه که 14 برش نیاز دارد.
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
زاویه، انواع آن و روابط بین آن ها
زاویه
دو نیم خط با رأس مشترک، زاویه ایجاد می کنند.
نام گذاری زاویه:
1- با حرف رأس:
یک حرف بزرگ انگلیسی
2- با حرف رأس و دو نیم خط:
سه حرف انگلیسی که حرف وسط (همان رأس) حرف بزرگ و حروف کناری (نیم خط ها) حرف کوچک استفاده می شود.
مانند:
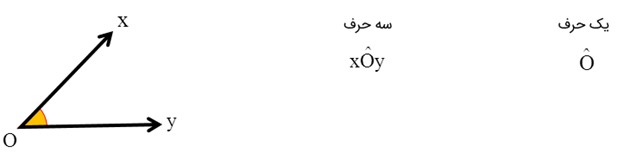
مثال
اگر ضلع های زاویه ای را چهار برابر کنیم، اندازه زاویه ... .
تغییری نمی کند.
اندازه زاویه هیچ ربطی به اندازه های ضلع های آن ندارد، پس هر چه اندازه های ضلع ها تغییر کنند، اندازه زاویه را تغییری نمی دهند.
انواع زاویه
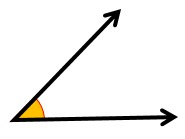
1- زاویه تند یا حاده:
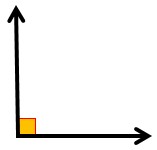
2- زاویه راست یا قائمه:
3- زاویه باز یا منفرجه:
4- زاویه نیم صفحه یا تخت:
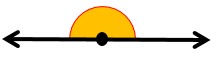
5- زاویه مقعر یا کاو (از ۱۸۰ تا ۳۶۰ درجه):

6- زاويه محدب یا کوژ (کمتر از ۱۸۰ درجه):
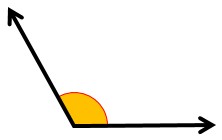
مثال
با توجه به شکل،
الف چند زاویه قائمه در شکل وجود دارد؟
ب به طور کلی چند زاویه در این شکل موجود است؟
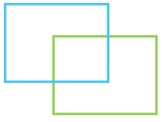
الف
زاویه قائمه زاویه ای است که 90 باشد. در شکل زیر، همه زاویه های قائمه مشخص شده اند (16 تا):
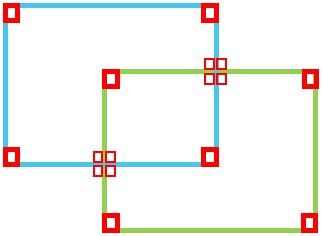
ب به طور کلی 16 زاویه در شکل موجود است.
زاویه های متمم:
دو زاویه (خواه کنار هم، خواه جدا از هم) که مجموع آنها ۹۰ درجه شود.
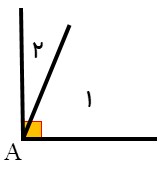
\({\hat A_1} + {\hat A_2} = {90^ \circ }\)
زاویه های مکمل:
دو زاویه (خواه کنار هم، خواه جدا از هم) که مجموع آنها 180 درجه شود.
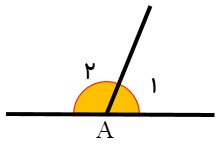
\({\hat A_1} + {\hat A_2} = {180^ \circ }\)
زاویه های متقابل به رأس:
دو زاویه که در رأس مشترک و اضلاع آنها در امتداد هم باشند.
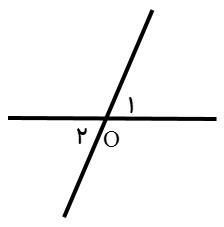
\({\hat O_1} = {\hat O_2}\)
دو زاویه متقابل به رأس همیشه با هم مساویند.
مثال
دو زاویه متقابل به رأس، مکمل اند، اندازه هر کدام برابر چند است؟
دو زاویه متقابل به رأس و مکمل \(\hat A\) و \(\hat B\) را در نظر بگیری:
\(\left. \begin{array}{l}\hat A = \hat B\\\hat A + \hat B = {180^ \circ }\end{array} \right\} \Rightarrow \hat A = \hat B = {90^ \circ }\)
روابط بین زاویه ها
با شناخت رابطه بین چند زاویه، می توان به رابطه های دیگری رسید؛ مانند:
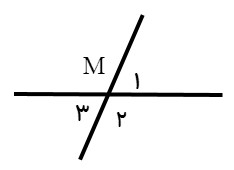
\(\left. \begin{array}{l}{{\hat M}_1} + {{\hat M}_2} = {180^ \circ }\\{{\hat M}_2} + {{\hat M}_3} = {180^ \circ }\end{array} \right\}\;\;\; \Rightarrow \;\;\;{\hat M_1} = {\hat M_3}\)
مثال
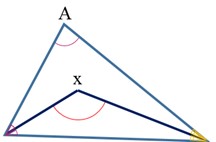
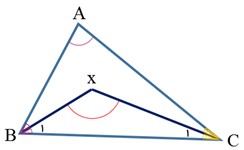
در مثلث زیر، زاویه A برابر با 80 درجه است. اگر نیمسازهای دو زاویه دیگر را رسم کنیم، اندازه زاویه x را بدست آورید.
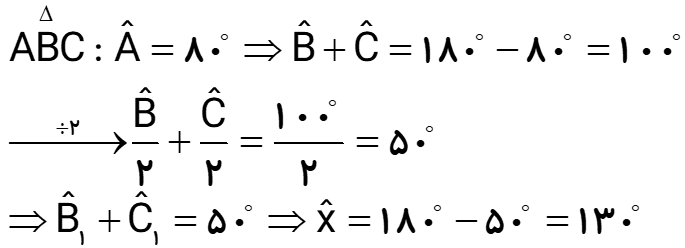
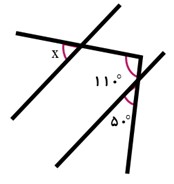
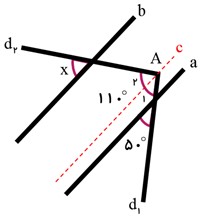
در شکل روبرو، زاویه x چند درجه است؟
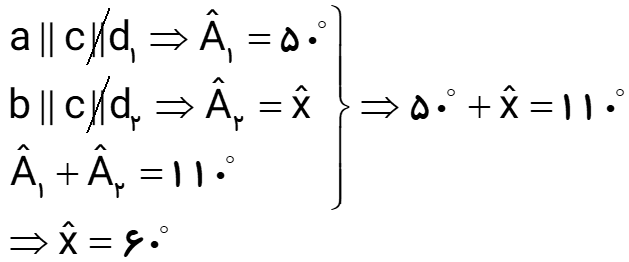
در شکل مقابل، مثلث متساوی الاضلاع CDE روی مربّع ABCD قرار دارد. زاویه BDC چند درجه است؟

از آنجایی که هر زاویه مثلث متساوی الاضلاع 60 درجه و هر زاویه مربع 90 درجه است و در مثلث متساوی الاضلاع، هر سه ضلع و هر سه زاویه برابر است، داریم:
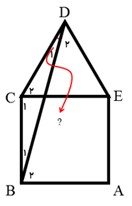
متساوی الاضلاع \(\,D\mathop C\limits^\Delta E \Rightarrow \overline {DC} = \overline {CE} \)
مربع \(ABCD \Rightarrow \overline {CE} = \overline {BC} \)
مثلث متساوی الساقین \(A\mathop E\limits^\Delta D \Rightarrow {\hat B_1} = {\hat D_1}\) \( \Rightarrow \overline {CD} = \overline {BC} \Rightarrow \)
\(\begin{array}{l}\left. \begin{array}{l}{{\hat C}_1} = {90^ \circ }\\{{\hat C}_2} = {60^ \circ }\end{array} \right\} \Rightarrow \hat C = {{\hat C}_1} + {{\hat C}_2} = {90^ \circ } + {60^ \circ } = {150^ \circ }\\\\{{\hat D}_1} + {{\hat B}_1} = {180^ \circ } - \hat C = {180^ \circ } - {150^ \circ } = {30^ \circ }\\\\{{\hat D}_1} = {{\hat B}_1} \Rightarrow 2{{\hat D}_1} = {30^ \circ } \Rightarrow {{\hat D}_1} = {15^ \circ }\end{array}\)
زاویه بین عقربه های ساعت
زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت h و دقیقه m از رابطه زیر به دست می آید:
\(\hat A = \left| {30h - \frac{{11}}{2}m} \right|\)
البته اگر مقدار زاویه بدست آمده بیشتر از 180 درجه شد، زاویه بدست آمده را از 360 درجه کم می کنیم.
مثال
زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت زیر را بیابید.

ساعت اکنون 10:10 می باشد که در این صورت:
\(h = 10\,\;\,\,\,\,,\;\,\,\,\,m = 10\)
\(\begin{array}{l}\hat A = \left| {30h - \frac{{11}}{2}m} \right| = \left| {30 \times 10 - \frac{{11}}{2} \times 10} \right| = \\\\300 - 55 = {245^ \circ }\end{array}\)
چون مقدار 245 درجه از 180 درجه بیشتر است، این عدد را از 360 درجه کم می کنیم:
\({360^ \circ } - {245^ \circ } = {115^ \circ }\)
در نتیجه زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت برابر 115 درجه می باشد.
زاویه بین عقربه های ساعت شمار و دقیقه شمار در ساعت 6:15 را بیابید.
\(\begin{array}{l}h = 6\,\;\,\,\,\,,\;\,\,\,\,m = 15\\\\\hat A = \left| {30h - \frac{{11}}{2}m} \right| = \left| {30 \times 6 - \frac{{11}}{2} \times 15} \right| = \\\\180 - 82/5 = - {97/5^ \circ }\end{array}\)
چند ضلعی ها
مثلث
در هر مثلث مجموع زاویه ها برابر ۱۸۰ درجه است.
مثلث ها را با توجه به اندازه زاویه هایشان به سه دسته تقسیم می کنیم:
1) مثلث هایی که هر سه زاویه آنها تند است.
2) مثلث هایی که یک زاویه راست دارند.
3) مثلث هایی که یک زاویه باز دارند.
4) یک مثلث را وقتی نمی توان کشید که اندازه هر ضلع آن مساوی با بزرگتر از جمع دو ضلع دیگرش باشد:
جمع دو ضلع دیگر > اندازه هر ضلع
5) مثلث مختلف الاضلاع را می توان با «سه زاویه تند» یا «یک زاویه قائمه و دو زاویه تند» و یا «یک زاویه باز و دو زاویه تند» رسم کرد.
6) مثلث متساوی الساقین را می توان با «سه زاویه تند» یا «یک زاویه قائمه و دو زاویه تند» و با «یک زاویه باز و دو زاویه تند» رسم کرد.
7) مثلث متساوی الاضلاع را فقط با سه زاویه تند ( زاویه 60 درجه) می توان رسم کرد.
مثال
آیا با عدد های 5، 12 و 13 می توان مثلث رسم کرد؟
جهت رسم یک مثلث، برای تمام اضلاع باید رابطه زیر برقرار باشد:
جمع دو ضلع دیگر > اندازه هر ضلع
بنابراین:
\(\begin{array}{l}5 < 12 + 13 = 25\\\\12 < 5 + 13 = 18\\\\13 < 5 + 12 = 17\end{array}\)
پس با این اضلاع حتما می توان یک مثلث رسم کرد.
طول دو ضلع مثلثی 7 و 4 می باشد. اندازه ضلع سوم را بررسی کنید.
همان طور که می دانیم برای رسم یک مثلث بایستی هر سه ضلع از قانون زیر تبعیت کنند:
جمع دو ضلع دیگر > اندازه هر ضلع
بنابراین:
\(\,\, < 4 + 7 = 11\)اندازه ضلع سوم
اندازه ضلع سوم باید حتما کمتر از 11 باشد.
نکاتی درباره چند ضلعی ها
1 چند ضلعی هایی که هیچ زاویه بزرگتر از ۱۸۰ درجه ندارند، «چند ضلعی محدب یا کوژ» نامیده می شوند.
2 به چند ضلعی ای که دست کم یک زاویه بزرگتر از ۱۸۰ داشته باشد، «چند ضلعی مقعر یا کاو» می گویند.
3 به چند ضلعی هایی که همۀ ضلع ها و زاویه هایشان با هم مساوی است، «چند ضلعی منتظم» گفته می شود، مانند مثلث متساوی الاضلاع، مربع و ... .
4 مجموع زاویه های هر n ضلعی برابر است با:
\((n - 2) \times 180\)
که n تعداد اضلاع است.
5 اندازه هر زاویه هر n ضلعی منتظم برابر است با:
\(\frac{{180 \times (n - 2)}}{n}\)
6 تعداد قطرهای هر n ضلعی برابر است با:
\(\frac{{n \times (n - 2)}}{2}\)
مثال
مجموع زوایای یک 8 ضلعی را بیابید.
\(\begin{array}{l}n = 8\\\\ \Rightarrow (n - 2) \times {180^ \circ } = (8 - 2) \times {180^ \circ } = 6 \times {180^ \circ } = {720^ \circ }\end{array}\)
تعداد قطرهای یک 8 ضلعی را بیابید.
\(\begin{array}{l}n = 8\\\\ \Rightarrow \frac{{n \times (n - 2)}}{2} = \frac{{8 \times (8 - 2)}}{2} = \frac{{8 \times 6}}{2} = \frac{{48}}{2} = 24\end{array}\)
اندازه یک زاویه داخلی 5 ضلعی منتظم را بیابید.
\(\begin{array}{l}n = 5\\\\ \Rightarrow \frac{{{{180}^ \circ } \times (n - 2)}}{n} = \frac{{{{180}^ \circ } \times (5 - 2)}}{5} = \\\\\frac{{{{180}^ \circ } \times 3}}{5} = \frac{{{{540}^ \circ }}}{5} = {108^ \circ }\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
تبدیلات هندسی (انتقال، تقارن و دوران)
اگر شکل را بدون تغییر جهت روی صفحه حرکت دهید تا تصویر آن جابجا گردد، بدین ترتیب شکل را روی صفحه انتقال داده اید.
وقتی قرینه شکلی را نسبت به یک خط (خط تقارن) پیدا می کنیم، تصویر به دست آمده مساوی آن شکل است، اما جهت آن تغییر می کند.
مرکز دوران:
نقطه ای است که شکل حول آن گردش (یا دوران) می کند.
در دوران ۱۸۰ درجه نسبت به مرکز دوران، شکل به اندازه یک زاویه نیم صفحه (۱۸۰ درجه) گردش خواهد داشت.
در دوران ۹۰ درجه نسبت به مرکز دوران، شکل به اندازه یک زاویه قائمه (۹۰ درجه) گردش می کند. این گردش به دو صورت امکان پذیر است. خلاف عقربه های ساعت، که گردش ۹۰ درجه به سمت راست و در جهت عقربه های ساعت که گردش ۹۰ به سمت چپ شکل اولیه صورت می گیرد.
مثال
کدام یک از گزینه های زیر دوران یافته شکل مقابل است؟
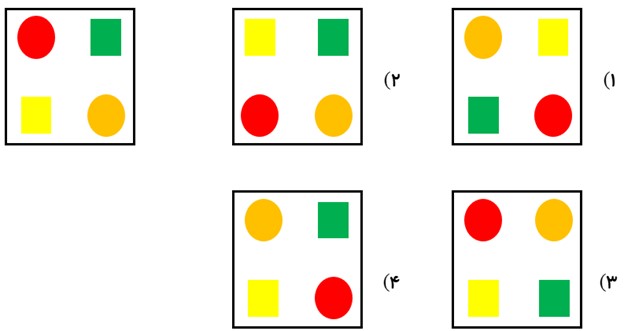
گزینه (1) جواب صحیح می باشد.
شکل های مساوی (هم نهشت)
اگر بتوانیم شکلی را با یک یا چند تبدیل انتقال، تقارن یا دوران در صفحه بر شکل دیگر منطبق کنیم، می گوییم این دو شکل با هم هم نهشت (مساوی) اند. این تبدیل ها به ← مشخص می گردد که نوع تبدیل بالای فلش نوشته می شود.
مثال
اگر دو شکل زیر هم نهشت باشند، مقادیر x و y را بیابید.
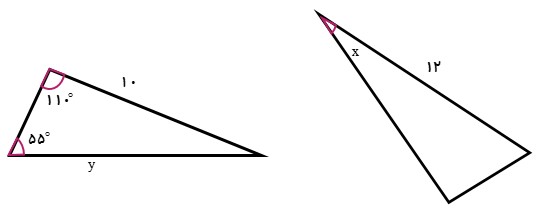
ابتدا راس هر مثلث را نام گذاری می کنیم تا اضلاع و زاویه های متناظر را تعیین کنیم:
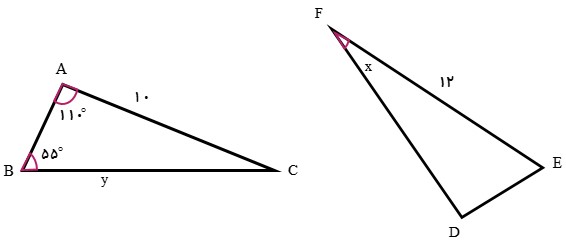
\(\left\{ \begin{array}{l}\hat A = \hat D\\\hat B = \hat E\\\hat C = \hat F\end{array} \right.\,\,\,\,\,\,,\,\,\,\,\,\,\,\left\{ \begin{array}{l}\overline {AB} = \overline {DE} \\\overline {AC} = \overline {DF} \\\overline {BC} = \overline {EC} \end{array} \right.\)
در نتیجه مقادیر x و y به صورت زیر می باشند:
\(\begin{array}{l}x = \hat F = \hat C = {180^ \circ } - (\hat A + \hat B)\\\\ \Rightarrow x = {180^ \circ } - ({110^ \circ } + {55^ \circ }) = {15^ \circ }\\\\y = \overline {BC} = \overline {EF} \Rightarrow y = 12\end{array}\)



1736019749.png)